线弹性范围内钢悬臂梁的阻尼特性试验研究①

谢伟平， 郭 漫， 孙亮明

(武汉理工大学土木工程与建筑学院， 湖北 武汉 430070)

线弹性范围内钢悬臂梁的阻尼特性试验研究①

谢伟平， 郭 漫， 孙亮明

(武汉理工大学土木工程与建筑学院， 湖北 武汉 430070)

采用材质相对均匀、结构较为简单的钢悬臂梁为试验对象，通过自由振动试验，研究了阻尼比的变化规律。设计制作了4根相同的矩形截面钢悬臂梁，根据国家标准规定的试验方法对材料力学性能进行了测试，得到了弹性模量和拉压强度。采用自由衰减法对钢悬臂梁进行不同初始振动幅度下的自由振动测试，识别不同振动幅度时悬臂梁的阻尼比。研究结构构件在自由振动下阻尼比的变化规律，分析线弹性范围内阻尼比与振动幅度的关系，得出以下结论：线弹性范围内，悬臂梁自由振动的阻尼比随其振动幅度的增加而增大，为结构在小幅度振动下的动力分析提供了参考依据。

阻尼比; 悬臂梁; 线弹性; 自由振动试验; 应变

引 言

任何建筑都具有一定的阻尼性能，阻尼与刚度和质量一样，是工程结构固有的动力特性之一。结构的阻尼性能对于结构的动力特性有着很重要的影响，阻尼比取值的些微差别都会导致结构动力响应分析的巨大变化，在建筑设计中，阻尼比的取值十分关键[1-2]。因此，人们逐渐提高了对结构的阻尼特性研究的关注和投入[3-6]。

工程结构的阻尼一般通过实测得到，实测阻尼包含材料阻尼、结构阻尼、介质阻尼三个部分。各个国家规范所给出的阻尼比的取值，绝大部分来自于工程结构在极限状态时的实测值，且一般认定阻尼比为常数。此外，结构的变形进入弹塑性阶段后，结构阻尼比具有明显的非线性性质，即阻尼比的值会随着结构的应力状态、振幅等的改变而发生较大的变化。一般认为，如果结构的变形未超过弹性变形阶段时(已处极限状态)，则其阻尼比的取值范围对钢结构来说是1%～2%，对钢筋混凝土结构而言是3%～8%；但是，当达到弹塑性阶段后，如果结构振动响应增加，则其阻尼比会跟着提高[7]。但是，国内外学者研究发现即使在线弹性工作阶段，结构的阻尼比也具有非线性性质，结构的阻尼比也会随着振动幅度变化而变化[8-11]。最近10多年，随着现代社会科技的进步，国内外学者通过实测对结构阻尼的研究逐渐取得了较多进展，但是还远远不够[12-19]。目前建筑结构高度和跨度都相继增大，其刚度随之越来越小，导致一系列振动舒适度问题出现，例如人行桥人致振动、大跨度车站结构的振动问题等。这些问题中结构的振动幅度较小，变形尚在线弹性范围阶段，因此有必要探讨结构在线弹性阶段的阻尼特性。

综上所述，为了能定量研究线弹性范围内阻尼比与振动幅度的关系，本文将采用最简单的构件——悬臂梁为试验对象[20-21]，其材料选取均质的钢材，其截面形式选用实际工程结构中常见的矩形截面，进行不同初始条件下的自由振动阻尼比测试。之后，通过测试得到的加速度时程响应，采用自由衰减法分别识别出不同振动幅度下的结构的阻尼比，从而定性、定量的分析线弹性范围内钢悬臂梁自由振动的阻尼比与振动幅度之间的关系。

1 材料拉伸试验

本文制作成悬臂梁的钢条选自同一块钢板，阻尼比试验前对钢条进行材料的拉伸试验，继而对钢悬臂梁的材料力学性能进行了试验分析。

1.1 试验原理

按照国家标准《金属材料拉伸试验》(GB/T 228.1—2010)，制作了如图1所示的4根标准试样，并进行编号。然后在室温条件下分别对其进行了金属材料的拉伸试验，主要是测定钢悬臂梁在轴向静载拉伸过程中的力学特性，包括材料的弹性模量、抗拉屈服强度以及极限抗拉强度。

图1 拉伸试验的标准试样Fig.1 The standard specimens of tensile test

1.2 试验仪器

拉伸试验采用的是美特斯工业系统(中国)有限公司生产的微机控制电子万能试验机，其具体参数如表1所示。

表1 万能试验机的参数

1.3 试验结果及分析

测量试件的弹性模量时，为提高试验结果的准确性，每根试件采用同一程序测量两遍。拉伸曲线如图2所示，可知试样的变形基本符合胡克定律。

根据弹性模量测量原理，计算4个试样的弹性模量，计算结果如表2所示。因此，钢悬臂梁构件的弹性模量取4个试样弹性模量的均值，为214703.30 N/mm2。测得的拉伸曲线如图3所示。试验时，由试样断裂前后的变化可见，试样基本呈塑性破坏。试样断口所在位置都在试样的平行长度部分，满足正常断口位置的要求。本次试验中各个试样的记录值如表3所示。

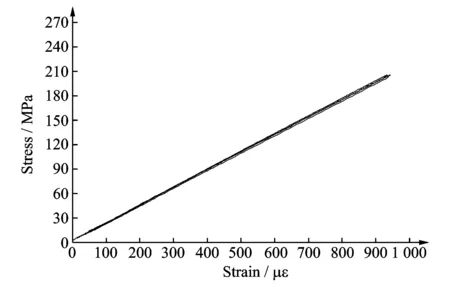
图2 试样应力-应变曲线Fig.2 Stress-strain curve for the specimens

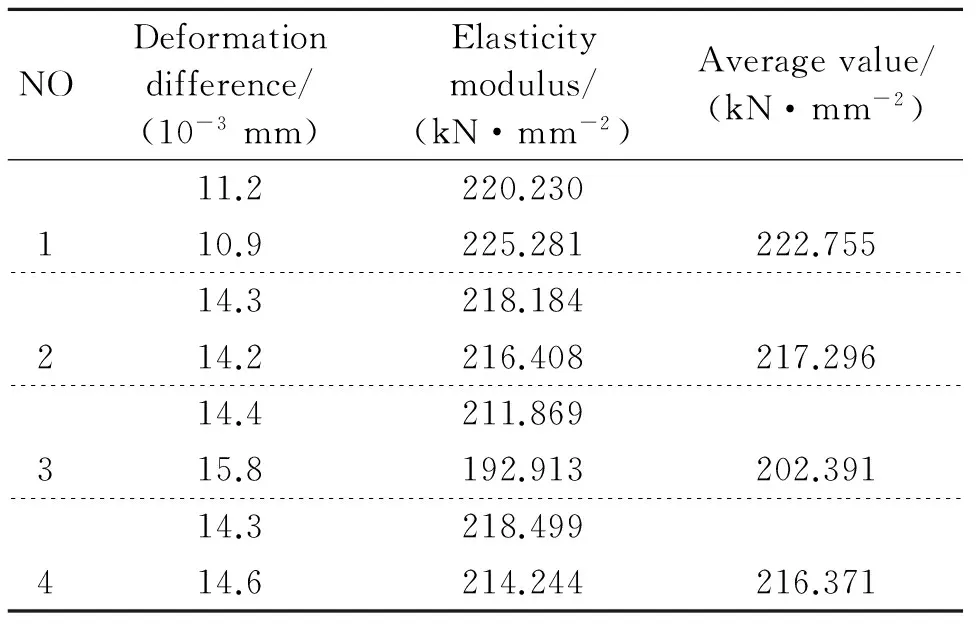
表2 试样的弹性模量Tab.2 The elasticity modulus of the specimens

图3 试样拉伸曲线Fig.3 The tensile curve for the specimens

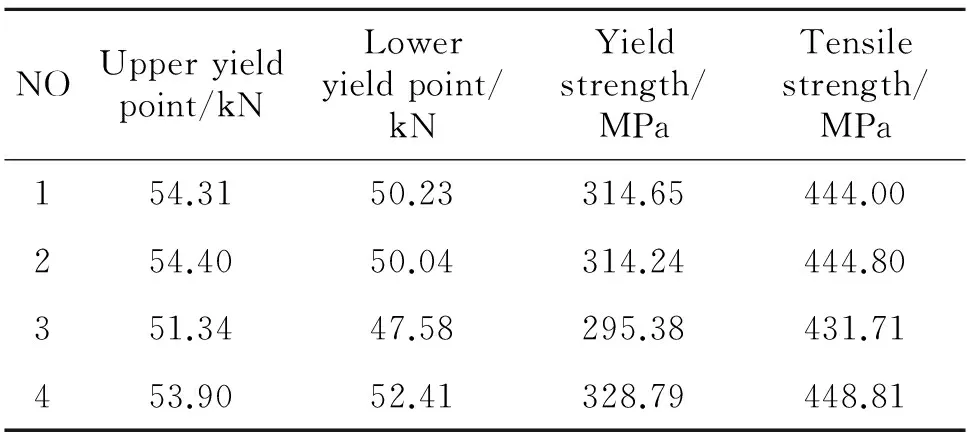
表3 试样的拉伸强度

为了保证悬臂梁构件的阻尼比试验是在其线弹性范围内进行的，需取试样中最小的拉伸强度为临界值，因此抗拉屈服强度取为295.38 MPa，极限抗拉强度取为431.71 MPa。抗拉屈服强度对应的应变的量级为104με。

2 悬臂梁阻尼性能试验

2.1 试验原理

2.1.1 阻尼比的识别

对于单自由度体系而言，其黏滞阻尼比可通过自由振动的对数衰减率得到。对于小阻尼体系，可得其阻尼比计算表达式为

(1)

式中x为单自由度体系自由振动的位移响应，ξ为阻尼比，TD为振动周期，δ为对数衰减率。

由于实际测试时，加速度响应的测量精度较高且更容易测量，因此通常采用加速度传感器。这样得到的便是系统的加速度时程，容易证明，对于加速度时程，也可以用下式计算阻尼比

(2)

式中A为单自由度体系自由振动加速度响应的峰值，Ai为第i个峰值，Ai+n为第i+n个峰值。

在实际结构的测试过程中，由于测量总会受到各种各样的外界干扰，所以，实测加速度时程曲线会出现不规则的上下波动，导致波峰值的获取很难保证准确性。但是，外界的干扰对时程曲线与时间轴所围成的面积的影响将大大减小。因此，可以对自由衰减法做一点改进[23]。对于小阻尼体系有

(3)

式中ξ为阻尼比；Si，Si+1为振动加速度时程曲线与时间轴围成的相邻周期的面积。

对于本文阻尼性能试验中的悬臂梁而言，由于它属于无限自由度体系，故而实测时采集到的振动响应包含了好几阶的模态。因此，无法直接通过公式(3)进行阻尼比的识别。但是，可以采用适当的方法进行处理后识别：首先对试验所采集到的加速度时程响应进行傅里叶变换，得到悬臂梁的频谱图；然后，根据频谱图分析悬臂梁固有频率大概的频带范围，并据此对加速度时程进行FIR滤波。这样，通过滤波后所得到的加速度时程便是只包含悬臂梁第一阶模态的加速度响应时程，随即就可以利用公式(3)来识别阻尼比。

2.1.2 振动幅度

为了定量确定不同初始条件下悬臂梁的振动幅度，本次试验采用悬臂梁的最大应变代替位移来标定。对于纯弯曲悬臂梁，在自由端端部荷载作用下，最大弯矩在其固定端处，相应的最大应变也在固定端截面。对于本次试验中的矩形截面悬臂梁，其截面最大应变计算公式如下

(4)

式中F为在悬臂梁自由端施加的荷载，单位为N。由上式可知，当荷载以一定的数值ΔF增加时，最大应变也将以定值递增。

2.2 试验仪器

试验中振动加速度响应的测量仪器为丹麦B&K 3050-B-060型土木工程振动与噪声测试系统，测量加速度响应时采用4507-B-005振动传感器，其具体参数：1)灵敏度：97.78 mV/(m·s-2)；2)频率范围：幅值(10%)0.4 Hz～6 kHz，相位(±5°)2 Hz～5 kHz；3)加速度量程：±70 m·s-2；4)共振频率：固定安装共振频率为18 kHz，横向共振频率>18 kHz；5)温度范围：-54 ～100 ℃；6)灵敏度温度系数：+0.18%/℃。

试验中应变的测试仪器为武汉优泰电子技术有限公司的UT4908动静态应变采集分析系统。UT49系列动静态应变采集分析系统主要技术参数如下：1)通道数：8通道；2)测量范围：0～±100000 με(0.5 V桥压)；3)灵敏系数：k=2.00；4)平衡参数：自动±5000 με，时间约1 s；5)误差：±0.1%；6)采样精度：24位；7)采样速率：最低速率为1 Hz，最高速率为20.48 kHz(单通道)；8)工作环境：温度要求0～40℃，湿度要求40℃(20～90)%RH。

2.3 试验试件及测点的布置

本试验为对照试验，试验对象为4根物理特性基本一致的钢悬臂梁。从同一块钢板上利用水切割工艺处理得到的钢条，通过浇筑混凝土将其一端固定住，从而得到悬臂梁如图4所示。本次试验所采用的悬臂梁的尺寸是由钢板的切割工艺、悬臂梁的理论固有频率以及市场上现有的钢材原料等因素综合考虑决定的，悬臂梁的物理参数如表4所示。表中悬臂梁的密度是通过实际测量的质量和体积计算得到，弹性模量由材性试验得到。

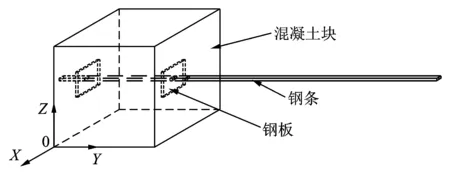
图4 悬臂梁示意图Fig.4 The diagram of the cantilever beam

表4 悬臂梁的物理参数

本次试验除了在悬臂梁上等间距布置4个加速度传感器之外，还在固定端的混凝土上也布置一个传感器，用来判断固定端的约束程度。同时，在悬臂梁靠近固端处布置一个应变片，如图5所示为悬臂梁测点布置的示意图。

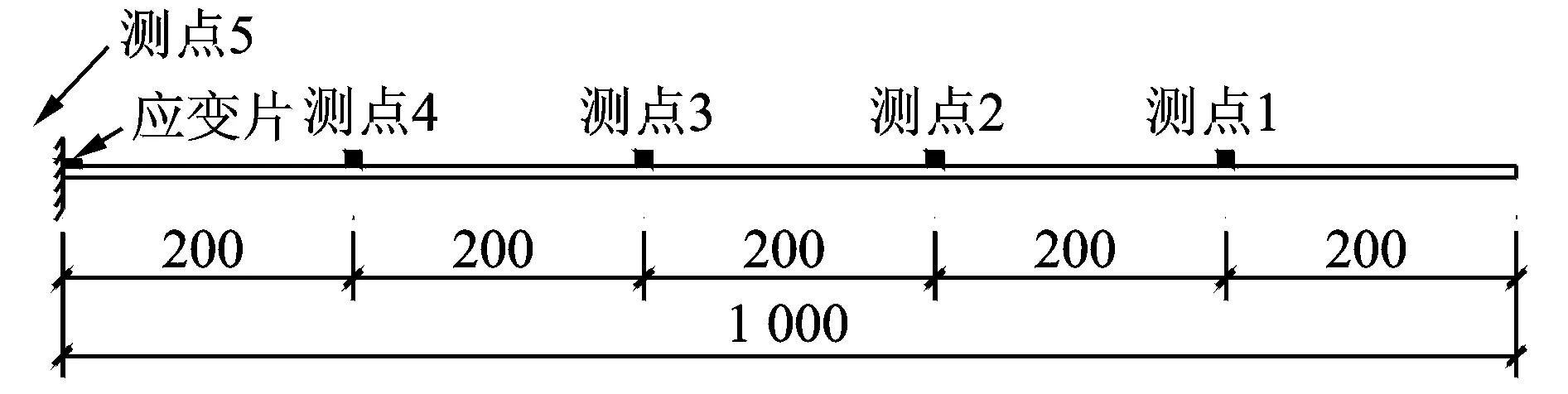
图5 悬臂梁测点布置示意图(单位：mm)Fig.5 The sensor placement of the cantilever beam (Unit: mm)

2.4 试验步骤

本次试验的试验对象为钢悬臂梁，共4根，试验前分别进行编号。每根悬臂梁根据不同加载质量相应地有28种工况，每种工况做3次试验，一次实验得到一组数据。具体的试验步骤流程如图6所示。

3 基于试验的钢悬臂梁阻尼特性研究

本文中悬臂梁阻尼性能试验是一组对照试验，为验证对照性，需将实测物理特性与ANSYS建立的有限元模型进行对比。对照试验设计成果后，采用相同的数据分析方法，分别计算各工况的应变和阻尼比，依次完成4根悬臂梁的试验结果的处理。然后基于计算所得的应变和阻尼比分别进行定性、定量分析，从而得出悬臂梁在不同振动幅度下的阻尼比的变化规律。

3.1 悬臂梁的振动频率

建立悬臂梁的有限元模型时，模型参数按照表4选取。加速度传感器为10 mm×10 mm×10 mm的正方体，质量为2 g。按照图5的布置位置，建立有限元模型，利用有限元模型计算出悬臂梁的前3阶横弯的振动频率分别为：f1=6.744 Hz，f2=42.256 Hz，f3=118.346 Hz。

图7 悬臂梁测点1～5的加速度时程图Fig.7 The acceleration time histories of the measured point 1～5 of the cantilever beam

以1号梁为例，取1号梁某一工况的某一组试验所测得的自由振动加速度响应进行说明。如图7所示依次为悬臂梁测点1，2，3，4，5的加速度时程图。对比图7中的(a)，(b)，(c)，(d)与(e)的加速度响应的幅值可知，测点5即悬臂梁固定端混凝土上的加速度响应相对于悬臂梁上的响应而言很小，基本相差三个量级，可以认为测点5的响应为环境振动响应。因此，进一步可以认定悬臂梁的固定基本接近理论固定端。

对采集到的加速度响应进行FFT变换，可得悬臂梁的振动响应的频谱特性，从而可得出悬臂梁的实测频率。取上述前4个测点的加速度时程作FFT变换，得到如图8所示的频谱图。

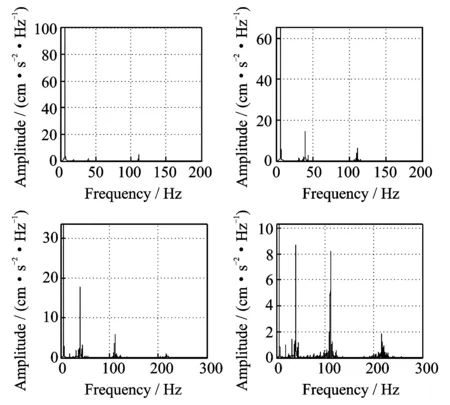
图8 悬臂梁测点1～4的加速度频谱图Fig.8 The acceleration spectra of the measured point 1～4 of the cantilever beam

由图8可知，试验时所采用的初始激励激起了悬臂梁的前5阶，甚至更高阶的模态，但是主要以前3阶模态为主。其中，测点1的振动响应基本只有一阶模态，这是由于测点1在2,3阶横弯零点的附近(由有限元模型得2阶横弯振型零点坐标为y=0.783 m，3阶横弯振型零点坐标为y=0.503 m，y=0.873 m，y为悬臂梁悬挑长度方向)，且靠近竖向荷载作用点的位置。测点3、测点4越来越接近固定端，激起的高阶模态振动越来越多。利用频谱分析计算悬臂梁测点1～4的前3阶频率，由计算结果可知，同一工况、同一组试验中，悬臂梁测点1～4的前3阶频率基本一致。

对不同工况的各组试验的频谱分析进行比较可知，同一工况、不同组的实测频率基本一致，而且不同工况的实测频率相差不大，故取它们的平均值代表每根悬臂梁的前3阶实测频率。悬臂梁的前3阶实测频率与理论频率的对比结果如表5所示。由表5可知，悬臂梁前3阶频率的理论值与实测值之间存在着一些差距。对于基频来说，实测值与理论值的差距在5.23%～6.20%之间。对于试验构件的2阶横弯振动频率来说，实测值与理论值的差距在5.11%～5.99%之间。对于试验构件的3阶横弯振动频率来说，实测值与理论值的差距在5.11%～6.00%之间。

表5 悬臂梁前3阶频率的实测值、理论值对比

Tab.5 The comparison between actual vibration frequency and computational vibration frequency for the cantilever beam

NO.f1/HzPercent/%f2/HzPercent/%f3/HzPercent/%L16.336.1339.935.51111.695.62L26.395.2340.105.11112.305.11L36.336.1539.735.99111.256.00L46.336.2039.845.71111.635.67

对比悬臂梁的前3阶振动频率的理论值和实测值可以发现，二者之间存在一定的差距。这是由于构件的悬挑长度、截面高度等参数与理论设计值有些偏差，而且实测弹性模量及实测密度取的是均值，与每根构件的实际弹性模量、实际密度也有些差异，但是总体而言还是比较正常的。对比各根悬臂梁之间的前3阶振动频率的实测值可以发现，差距很小，总体而言基本符合对照试验的要求。

3.2 悬臂梁的应变

试验时，取空载(仅有自重应变)为平衡点，故实测应变为荷载作用下的应变；加载稳定后即开始记录动态应变，故应变仪记录下了卸载前后应变的变化；由应变时程可知，卸载前的应变为定值，即为初始应变值，用以度量加载的大小。

对于每根悬臂梁而言，一个工况3组试验对应3个应变，理论上3个应变应该一致，实际测出的数值也基本一致。但是，有些工况的3组应变之间有些差异，若差异不大则取均值为该工况的应变；若差异明显很大的则去掉差异最大的值，取剩余应变的平均值作为该工况的应变。试验所得4根悬臂梁的加载与应变，根据每个工况的应变，线性拟合加载与应变的关系，拟合直线的斜率即为应变递增梯度。悬臂梁横截面宽度的实测值对应变梯度的影响很大，微小的变化会产生较大的改变。虽然试验设计悬臂梁横截面的宽度为3 cm，但是实际切割时，截面宽度会有一定的偏差。因此，实测的应变梯度与理论计算的值大5%～7%的，基本在误差允许的范围内。

将所有实测的应变数据进行线性拟合，如图9所示。

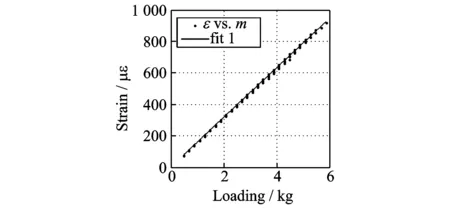
图9 加载质量-应变的拟合Fig.9 The curve fitting of loading and strain

通过拟合，可以得到本次阻尼比试验中，悬臂梁的加载质量与固定端处的应变的计算公式如下所示

ε=0.1572m+1.781

(5)

式中ε表示应变，单位为με；m表示悬臂梁自由端悬挂的质量，单位为g。理论上，悬挂质量为零时，应变也应该为零(试验时，悬挂砝码前对应变进行了自平衡，即清零，故所测应变不包括梁自重所产生的应变)。公式(5)显示，初始应变为1.781 με，与理论值并不相符。可以认为是试验装置、测试误差引起的，后续分析中可直接扣除该误差。

3.3 悬臂梁的阻尼比

试验时，为避免加速度超出量程而对数据处理结果产生影响，分析时首先将所有工况的所有测点的原始加速度时程从中间截取一段，取最大加速度对应的时间点延迟1 s后的点为起点；试验数据采集时，可观测到经历80 s后衰减基本结束，故取为终点。然后，对截断后的加速度时程响应进行FIR带通滤波，只留一阶模态响应，经过截断、滤波后的频谱图如图10所示。

对比图8与10可知，FIR带宽滤波后，测点加速度响应基本只有一阶模态了。之后，利用式(3)，用MATLAB拟合对数衰减率。曲线拟合结果表明加速度的衰减基本呈指数衰减，良好的拟合效果说明同一工况的一组试验中一个测点对应一个阻尼比值。

通过分析各根悬臂梁实测数据可知，同一工况的同一组测试的4个测点的阻尼比计算结果基本一致，如图11所示为1号梁各工况对应的测点1～4的阻尼比。通过图11可知测点4相对于其他测点而言，虽然阻尼比的变化规律相同，但是阻尼比值稍微偏小一点，这是由于测点4处加速度响应中高阶振型部分比重过大，滤波使其响应大幅度减小所致。由于测点1布置靠近高阶振型的零点处，故测点1处以一阶振动为主，因而以测点1处的阻尼比为主。

图10 滤波后测点1～4的频谱图Fig.10 The acceleration spectra of the measured point 1～4 after filtering

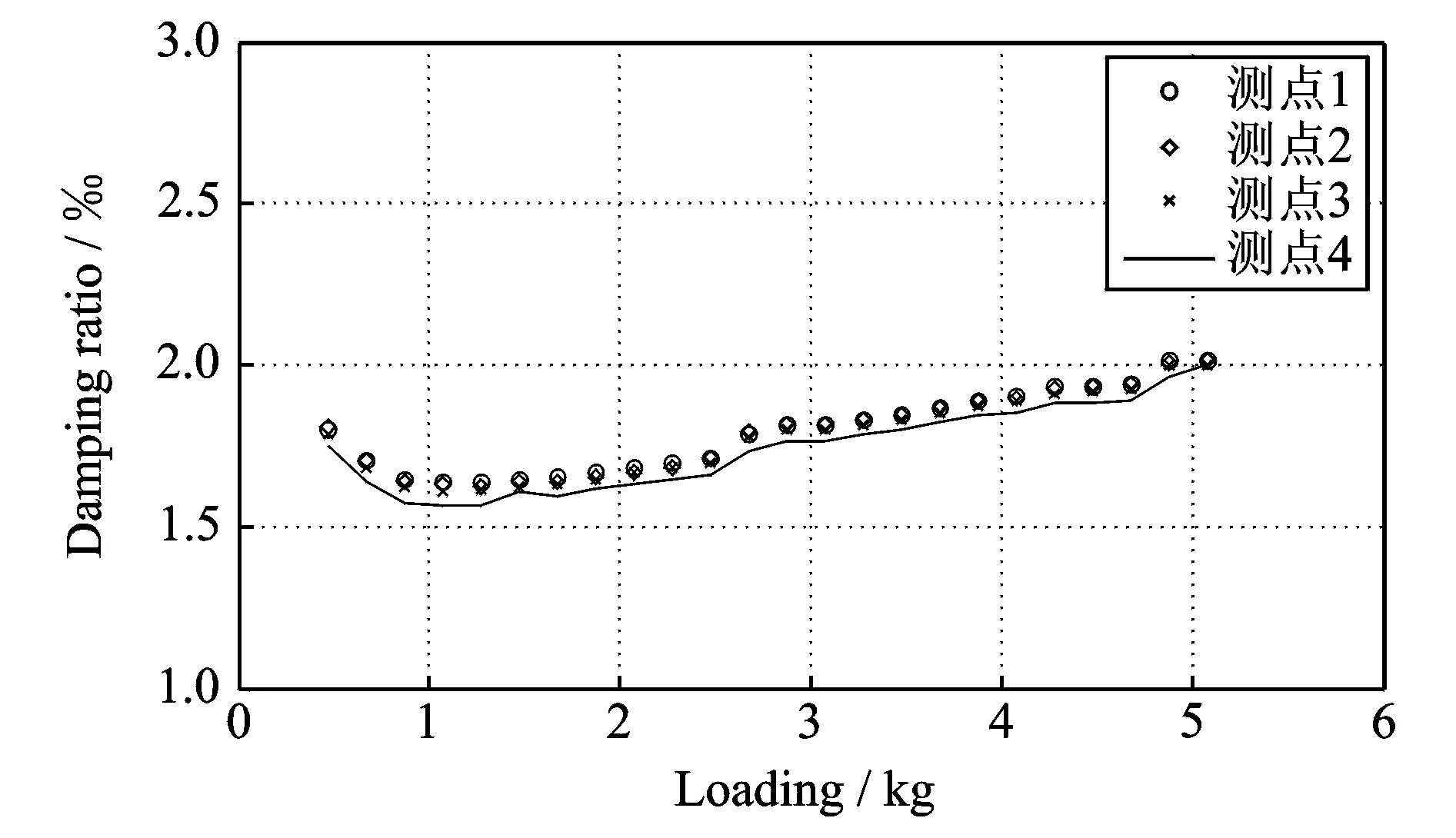
图11 测点1～4的实测阻尼比Fig.11 The test damping ratio of the measured point 1～4

同一测点在同一工况下的3组试验所测试的阻尼比大致相同。但是，有些工况的3组试验的阻尼比之间还是有些许差异的，若差异不大则取均值为该工况的阻尼比；若差异明显很大则去掉差异最大的值，取剩余阻尼比的平均值作为该工况的阻尼比。

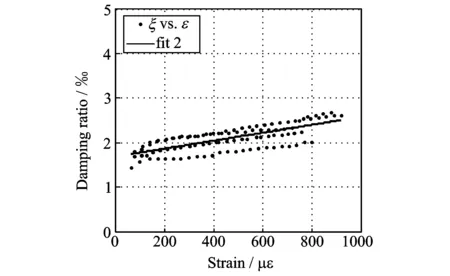
图12 悬臂梁应变-阻尼比的拟合结果Fig.12 The fitting result of strain and damping ratio of the cantilever beam

为了定量分析悬臂梁的阻尼比与应变的关系，将测量所得的全部数据进行集中分析。如图12所示，随着应变的增加，悬臂梁的阻尼比基本上呈线性增长，线性拟合的结果为

ξ=0.000894ε+1.682

(6)

式中ξ为阻尼比，量级为0.001；ε表示应变，单位为με。

由图12可知，悬臂梁振动时应变的变化范围为0～919.9 με，阻尼比的变化范围为0.0014～0.0027。对比图3可知，应变的变化范围在线弹性范围内，悬臂梁最大的振动幅度只达到了103量级，而其本身的抗拉屈服强度对应应变的量级为104，相差一个量级，说明试验相对振动幅度很小。本文试验中测得悬臂梁的阻尼比量级为10-3，以材料阻尼和介质阻尼为主，而目前规范给出的阻尼比取值都接近于结构的极限状态，包含材料阻尼、结构阻尼、介质阻尼，因此取值量级为10-2。说明即使在线弹性范围内，结构的振动幅度对其阻尼比也有影响。

4 结 论

本文以钢悬臂梁构件为试验对象，研究了结构构件在自由振动下阻尼比的变化规律，分析了线弹性范围内阻尼比与振动幅度的关系，得出了以下结论：

1)整个阻尼性能试验过程中，悬臂梁构件的应变是在0～919.9 με的范围内变化。由悬臂梁构件的材料拉伸试验，得到其弹性模量为214703.299 N/mm2、抗拉屈服强度为295.379 MPa(对应应变量级为104με)。对比发现试验中悬臂梁构件的应变变化范围远小于屈服时的应变，故变形一直处于线弹性的范围内；

2)线弹性范围内，在振动初始应变处于0～919.9 με范围内变化时，阻尼比是在0.0014～0.0027的范围内变化。对实测数据拟合分析得，悬臂梁的阻尼比以0.001682为初始值，并随应变的增加以0.000894的斜率线性递增；

3)线弹性范围内，对于均质性材料(钢材)的构件来说，其阻尼比是随着振动幅度的增加而线性递增的。

[1] 席尔瓦.振动阻尼、控制和设计[M].李惠彬,张曼等，译.北京:机械工业出版社, 2013.

Clarence W. de Silva. Vibration Damping, Control, and Design[M]. Beijing: China Machine Press, 2013.

[2] Anil K Chopra,著.结构动力学理论及其在地震工程中的应用[M].谢礼立,吕大刚，等,译.北京:高等教育出版社,2005.

Anil K Chopra. Dynamics of Structures Theory and Applications to Earthquake Engineering[M]. Beijing:Higher Education Press, 2005.

[3] 潘玉华.指数型阻尼模型及其在钢筋混凝土结构动力分析中的应用[D].北京:北京交通大学,2013.

Pan Yuhua. Exponential damping model and its applications to dynamic analysis of reinforced concrete structure[D]. Beijing: Beijing Jiaotong University, 2013.

[4] Abdelsamie Elmenshawi, Tom Brownb. Hysteretic energy and damping capacity of flexural elements constructed with different concrete strengths[J]. Engineering Structures, 2010,32(1):297—305.

[5] 吴启昌.材料及结构件阻尼特性的测量及应用研究[D].哈尔滨:哈尔滨工业大学, 2010.

Wu Qichang. Research on measurement and application of material and structural damping property[D]. Harbin: Harbin Institute of Technology, 2010.

[6] 马宁.几种构件的非比例阻尼比试验研究[J].工程抗震,2003,(1):37—41.

Ma Ning. Experimental study on the non-proportional damping ratio of several artifacts[J]. Earthquake Resistant Engineering, 2003,(1):37—41.

[7] 黄宗明,白绍良,赖明.结构地震反应时程分析中的阻尼研究[J].土木工程学报,1998,31(2):75—79.

Huang Zongming, Bai Shaoliang, Lai Ming. An investigation of damping in earthquake response time history analysis of structures[J]. China Civil Engineering Jounal, 1998,31(2):75—79.

[8] 樊海涛.钢筋混凝土建筑非线性阻尼性能及其地震反应研究[D].长沙:湖南大学, 2005.

Fan Haitao. The research on non-linear damping properties and seismic response of reinforced concrete buildings[D]. Changsha: Hunan University, 2005.

[9] 康希良.有机玻璃结构模型阻尼系数的试验确定及分析[J].兰州铁道学院学报,1994,13(4):8—13.

Kang Xiliang. Experiment determination and analysis on damping coefficient of organic glass structure model[J]. Jouranl of Lanzhou Railway Institute, 1994,(4):8—13.

[10]严佳佳.基于变形的钢筋混凝土结构阻尼参数研究[D].扬州:扬州大学,2012.

Yan Jiajia. Research on the damping parameters of reinforced concrete structure based on the deformation[D]. Yangzhou: Yangzhou University, 2012.

[11]黄宗明.结构地震反应时程分析中的阻尼研究[D].重庆:重庆建筑大学,1995.

Huang Zongming. An investigation of damping in earthquake response time history analysis of structures[D]. Chongqing: Chongqing Jianzhu University, 1995.

[12]黄本才.高层建筑钢结构振动阻尼比测试与分析[J].结构工程师,1997,(4):20—24.

Huang Bencai. Measurement and analysis of modal damping ratios on tall steel building[J]. Structural Engineers, 1997,(4):20—24.

[13]Morita K, Kanda J. Experimental evaluation of amplitude dependent natural period and damping ratio of a multi-story structure[C]. Proceedings of 11th World Conference on Earthquake Engineering, Mexico, 1996.

[14]桂堃.多功能钢结构电视结构阻尼的研究和实测[D].上海:同济大学,2002.

Gui Kun. Research and site experiment of multifunctional steel TV tower′s damp[D]. Shanghai: Tongji University, 2002.

[15]Li Q S, Yang K, Zhang N, et al. Field measurements of amplitude-dependent damping in a 79-storey tall building and its effects on the structural dynamic responses[J]. Structural Design of Tall Buildings, 2002,11(2):129—153.

[16]Kilpatricka J T, Kijewski T. Full scale validation of the predicted response of tall buildings: preliminary results of Chicago monitoring project[J]. Proceed-dings of 2003 Structures Congress, ASCE Seattle, 2003:433—440.

[17]陈丽,李秋胜,李正农,等.中信广场风场特性及风致结构振动的同步监测[J].自然灾害学报,2006,15(3):169—174.

Chen Li, Li Qiu-sheng, Li Zheng-nong et al. Simultaneous monitoring of wind characteristic and wind-induced vibration of main tower in CITIC Plaza[J]. Journal of Natural Disasters, 2006,15(3):169—174.

[18]Li Q S, Xiao Y Q, Fu J Y, et al. Full-scale measurements of wind effects on the Jin Mao building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007,95(6):445—466.

[19]潘戬.高层建筑结构风致振动阻尼比识别研究[D].哈尔滨:哈尔滨工业大学, 2012.

Pan Jian. Research on identification of damping ratio of wind induced vibration of high rise building[D]. Harbin: Harbin Institute of Technology, 2012.

[20]李晖,孙伟,张永峰，等.悬臂薄板结构阻尼特性几种测试方法的比较[J].中国工程机械学报,2013,11(4):347—353.

Li Hui, Sun Wei, Zhang Yong-feng, et al. Comparative study on testing methods for damping property of cantilever thin-plate structures[J]. Chinese Journal of Construction Machinery, 2013,11(4):347—353.

[21]Demarie G V, Sabia D. Non-linear damping and frequency identification in a progressively damaged R C element[J]. Experimental Mechanics, 2011,51(2):229—245.

[22]中华人民共和国规范标准.金属材料拉伸试验(GB/T 228.1-2010)[S].北京:中国标准出版社,2011.

The Standard of the People′s Republic of China. Metallic Materals—Tensile Testing(GB/T 228.1-2010)[S]. Beijing: Standards Press of China, 2011.

[23]冷巧娟.钢筋混凝土构件的阻尼特性和地震破坏模型研究[D].长沙:湖南大学, 2007.

Leng Qiaojuan. The research on damping and seismic damage model of RC element[D]. Changsha: Hunan University, 2007.

Experimental study on damping characteristics of the
steel cantilever beam in the linear elastic range

XIEWei-ping，GUOMan，SUNLiang-ming

(School of Civil Engineering and Architecture，Wuhan University of Technology， Wuhan 430070， China)

A relatively uniform and simple steel cantilever beam is used as the test object. And the free vibration test of the cantilever beam is carried out to investigate the variation of the damping ratio. The same four cantilever beams with rectangular cross-section have been designed and manufactured. Based on the national standard, the elastic modulus and tensile strength of the cantilever beam is obtained through the metallic materials tensile test. The vibration test under different initial conditions is carried out. The damping performance test is conducted by the free damping method. The purpose is to study the variation of damping ratio of the structure in the free vibration and analyze the relationship between the vibration amplitude and the damping ratio of the cantilever beam in the linear elastic range. These works in this paper make the following conclusions: the free vibration damping ratio of the cantilever beam is increasing with the increasing of vibration amplitude in the linear elastic range, and it provides a reference basis for the structure dynamic analysis under the condition of small amplitude vibration.

damping ratio; cantilever beam; linear elasticity; free vibration test; strain

2015-06-04；

2015-12-06

国家自然科学基金资助项目(51178365)

TU313.3

：A

1004-4523(2016)06-1011-09

10.16385/j.cnki.issn.1004-4523.2016.06.009

谢伟平(1965—),男,博士,教授。电话: 13871061394; E-mail: wpxie@sina.com

孙亮明(1983—)，男，博士，讲师。电话：13545909941; E-mail: sunliangming@126.com