多点激励正弦振动的实数域控制算法研究①

刘志华， 蔡晨光， 于 梅， 夏 岩， 李京胜

(中国计量科学研究院， 北京 100029)

多点激励正弦振动的实数域控制算法研究①

刘志华， 蔡晨光， 于 梅， 夏 岩， 李京胜

(中国计量科学研究院， 北京 100029)

多点激励正弦振动系统能更加真实地模拟实际振动环境，更利于掌握产品的实际振动特性。针对传统频域迭代算法中复数计算的求解复杂性，对实数域控制算法进行研究。建立多点激励正弦振动控制的实数域数学模型，采用Broyden算法构建实数形式的阻抗矩阵，并对迭代步长进行优化，在此基础上提出实数域迭代算法的控制流程。最后对算法的可行性进行仿真分析和实验验证，结果表明：实数域控制算法的收敛速度快、响应精度高，且可以有效避免振荡过冲现象。

振动控制； 多点激励； 拟牛顿算法； 实数域

引 言

传统的振动环境试验广泛采用单点激励振动系统，但随着产品结构的复杂化和多样化，人们逐渐开始关注多点激励振动系统，其优势在于不仅能够提供足够的推力而且能更加真实地模拟实际振动环境，更利于掌握产品的实际振动特性[1-2]。正弦振动试验是一类重要的振动环境试验，有助于暴露零部件或设备在特定激励频率下的故障缺陷[3]。相比于单点正弦激励控制，多点激励正弦振动控制除了要控制激励点幅值大小，还需考虑各激励点之间的互耦补偿以及相位差修正[4-5]。因此，多点激励正弦振动控制具有一定的难度与挑战性。

多点激励正弦振动控制的研究始于1973年，Fisher论述了互耦补偿方式的多点激励数字控制的理论与实践，为多点激励振动控制提供了理论依据[6]。Hamma和Smith提出了线性控制算法，采用误差频谱和当前驱动频谱之和来修正命令驱动频谱，算法简单但稳定性较差[7]。Chen和Wilson采用迭代增益来控制误差频谱补偿量，提高了正弦振动控制的稳定性但却减慢了收敛速度[8]。目前广泛应用的控制方法为提前激励系统来测量估计系统频响函数，进一步计算阻抗矩阵，完成对驱动信号的迭代修正[9-10]。但此类方法采用固定的迭代增益和阻抗矩阵，初始的阻抗矩阵误差会对控制系统的稳定性和精度产生持续性影响[11]。Underwood提出多点激励正弦试验的自适应控制方法，通过可变增益来控制迭代步长，并在迭代中不断更新系统阻抗矩阵，补偿系统的非线性和时变性影响[12-13]。国内学者陈家焱提出多点激励正弦振动的最优控制策略，以响应谱和参考谱的误差矢量范数为目标函数，采用“双步控制闭环”方法来确定并优化控制系统的迭代步长和驱动信号[14]。然而现存控制方法均为频域迭代算法，系统传递函数为复数矩阵，需要在复数域空间确定迭代步长和阻抗矩阵，增加了控制算法复杂度。

本文针对传统频域迭代算法的不足，提出多点激励正弦振动控制的实数域控制算法。首先，建立正弦振动的实数域控制数学模型，根据系统响应构建阻抗矩阵，并对迭代步长进行优化，在此基础上给出实数域迭代算法的控制流程。最后，对实数域迭代算法进行仿真分析，并通过实验进行验证。

1 实数域控制算法

1.1 数学模型

传统的多点激励正弦振动控制方法为频域迭代算法，如图1所示，需要提前激励系统来获取频响函数估计并计算阻抗矩阵，控制目标为使测量的响应频谱达到理想的参考频谱，通过反复迭代修正驱动信号，使系统输出的响应信号不断趋近设定的参考信号，驱动频谱的修正方程可以描述为

Dn+1(f)=Dn(f)+αZ(f)(R(f)-Cn(f))

(1)

式中Dn(f)为第n次迭代驱动谱；Dn+1(f)为所求的第n+1次迭代驱动谱；Z(f)为系统阻抗矩阵，通常取为系统频响函数估计值A(f)的逆矩阵A-1(f)；α为迭代增益，由于估计的频响函数与真实的频响函数难免存在一定误差，因此通常选取迭代增益0<α<1以提高控制系统的稳定性。

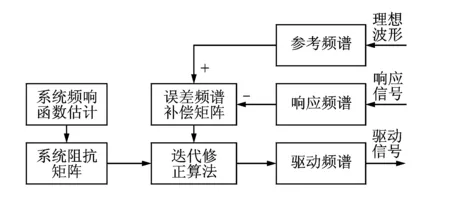
图1 频域迭代算法Fig．1 Iterative method in the frequency domain

传统频域迭代算法所开展的提前激励增加了振动控制过程的额外工作量，多点激励振动系统的频响函数识别往往耗时较长，明显增加了振动试验时间，而且还可能会对一些精密或易碎的试验样本造成不必要的损坏[15]。除此之外，传统频域迭代算法基于系统频响函数，多点激励振动系统的频响函数为复数域矩阵，限制了一些较为有效的实数域算法在振动控制领域的应用。因此，为了避免频域迭代算法的提前激励，将采用实数域控制算法来解决多点激励正弦振动控制问题。

系统的频响函数h(f)是一个包含幅值α和相位β的复指数

h(f)=αejβ

(2)

系统在频率ω、幅值C和相位φC的正弦信号x(t)激励下，将输出同频率的正弦信号y(t)：

x(t)=Csin(ωt+φC)

(3)

y(t)=αCsin(ωt+φC+β)

(4)

任意的正弦输入信号都可以变换成如下形式

(5)

其中，w1和w2为输入系数

w1=Ccos(φC),w2=Csin(φC)

(6)

同样，任意的正弦输出信号也可以变换为

(7)

其中，u1和u2为输出系数

(8)

通过式(5)和(7)的变换，系统的输入和输出均被表示成相互正交的正余弦函数之和的形式，如图2(a)所示，而输入和输出信号的幅值和相位由正余弦函数的系数决定。由于输入和输出均为标准正弦信号，振动控制中往往仅关心其幅值和相位，因此可将系统进行简化，如图2(b)所示，其中输入为u(t)，输出为w(t)，传递特性为h(t)，则由式(8)可以得到

u(t)=h(t)w(t)

(9)

其中：

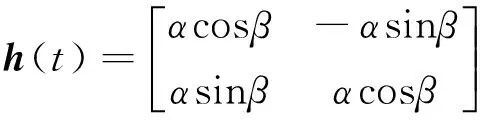
(10)

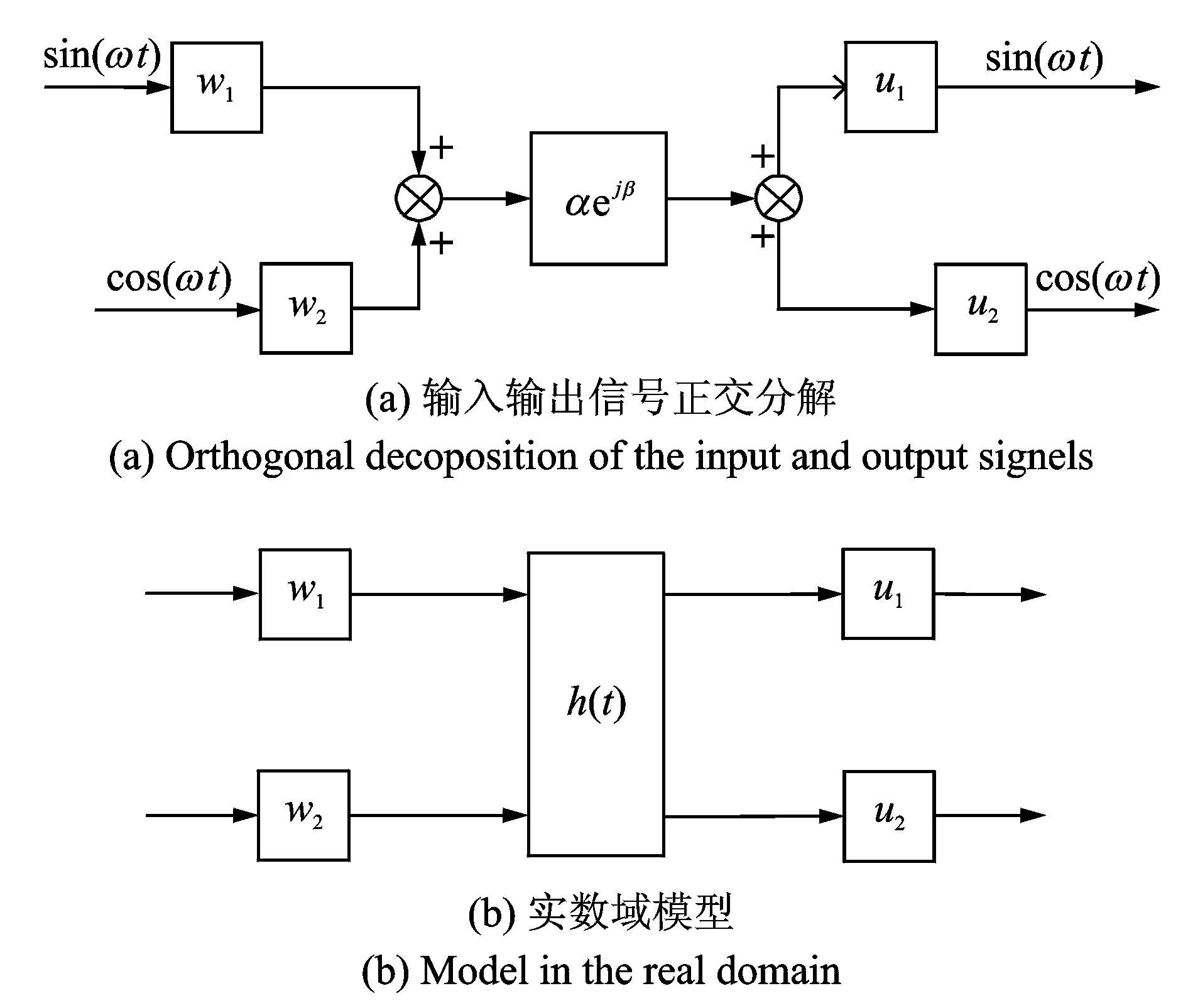
图2 系统模型化简Fig．2 Simplified system model

式(9)所描述的系统传递模型采用两个实系数来代替原本的一维正弦信号，虽然增加了系统的维度，但没有添加任何额外信息，因为正弦信号包含了幅值和相位。若不增加维度就要采用包含实部和虚部的复数表示，由此提出的复数域控制算法往往较为复杂。式(9)通过增加维度将复数域问题转换成实数域问题，便于实数域控制算法的提出。

同理，可以建立多点激励正弦振动系统的实数域数学模型

C(t)=H(t)D(t)

(11)

式中D(t)为系统驱动系数，C(t)为系统响应系数，H(t)为系统传递特性。

(12)

式中ui(t)为激励点i的响应系数，wi(t)为激励点i的驱动系数，hij(t)为激励点j和激励点i之间的传递特性，m为激励点的总个数。

1.2 阻抗矩阵

假设系统的参考系数为R(t)，系统的响应系数为C(t)，可以定义系统的误差系数如下

F(D(t))=R(t)-C(t)=

R(t)-H(t)D(t)

(13)

多点激励正弦振动控制的目标为求解合理的驱动系数D(t)，使得响应系数C(t)尽量接近参考系数R(t)，即求解方程F(D(t))=0。若不进行提前激励，无法获得系统的传递特性H(t)，因此将无法直接求解方程F(D(t))=0的导数值，只能获得方程函数值，此时可采用如下拟牛顿方法进行求解[16]

(14)

其中：

sn+1(t)=Dn+1(t)-Dn(t)，

yn+1(t)=F(Dn+1(t))-F(Dn(t))

(15)

式(14)中An+1(t)是对方程导数矩阵F′(D(t))的近似，通过修正矩阵ΔAn(t)迭代求得。但式(14)必须在增加适当条件下才能完全确定An+1(t)。Broyden算法要求An+1(t)和An(t)在向量sn+1(t)的正交补上二者无任何差别，即

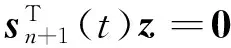
(16)

假定u(t)为待定向量，则由式(16)可以得到

(17)

由式(14)中的方程二可以得到

(An+1(t)-An(t))sn+1(t)=

yn+1(t)-An(t)sn+1(t)

(18)

将式(17)的两边右乘sn+1(t)，并联立式(18)可得到

(19)

将式(19)得到的u(t)代入式(17)便可得到An+1(t)的修正方程

(20)

根据式(20)对An+1(t)进行修正后，还需要通过求解线性方程组才能获得驱动系数Dn+1(t)。为了求解方便，根据Sherman-Morrison定理[16]可对An+1(t)的逆矩阵Zn+1(t)进行更新

(21)

通常将Zn+1(t)称为系统的阻抗矩阵，它是一个有别于传统频域迭代算法中的阻抗矩阵的实数矩阵。于是可以获得驱动系数的修正方程如下

Dn+1(t)=Dn(t)-Zn(t)(R(t)-Cn(t))

(22)

式(21)和(22)即为求解实数域非线性方程组的Broyden算法，在多点激励正弦振动控制应用中不需要进行系统辨识，从而避免了提前激励。

1.3 迭代步长

理论上按照式(22)的迭代公式便能够求解得出满足系统响应要求的驱动系数Dn+1(t)，而阻抗矩阵Zn(t)在迭代过程中将逐渐趋近于传递特性H(t)的逆矩阵。由于迭代开始阶段的阻抗矩阵往往与H(t)的逆矩阵偏差较大，因此采用失真的阻抗矩阵修正的驱动系数会造成系统响应的振荡，而在实际控制中应该尽量避免这种情况的出现。为此将式(22)的驱动系数迭代公式修改如下

Dn+1(t)=Dn(t)-λZn(t)(R(t)-Cn(t))

(23)

式中λ为迭代步长，用以合理控制驱动系数的修正量。如图3所示，阻抗矩阵Zn(t)决定了驱动系数的修正方向，而迭代步长λ则决定了驱动系数的修正量，事实上任意修正方向上均存在一个最接近目标值的局部极点，此局部极点可通过寻优迭代步长求得，以本局部极点为起点沿更新的阻抗矩阵方向，通过寻优迭代步长便可求得下一个局部极点，随着迭代过程局部极点将逐渐靠近目标值。所求得的局部极点是当前修正方向下最接近目标值的驱动系数，从而有效避免了控制过程的振荡现象。

将误差系数的矢量范数作为目标函数，用以衡量响应系数C(t)与参考系数R(t)的接近程度

f(Dn+1(t))=(R(t)-Cn+1(t))T(R(t)-Cn+1(t))

(24)

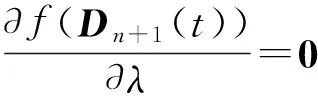
λ=-{H(t)Zn(t)(R(t)-Cn(t))]T(R(t)-Cn(t))}/

{H(t)Zn(t)(R(t)-Cn(t))]T[H(t)Zn(t)(R(t)-Cn(t))}

(25)

式(25)的迭代步长求解表达式中包含有未知的系统传递特性H(t)，因此需要根据系统响应系数对系统的传递特性进行估计。为准确估计当前状态系统传递特性，驱动系数的变化量应尽可能小，采用取值很小的迭代步长ρ(通常为0.1)修正驱动系数

(26)

由式(27)可以进一步推导得出

H(t)Zn(t)(R(t)-Cn(t))=

(28)

将式(28)代入式(25)可以消去方程中的未知量，得到最优步长的求解公式如下

(29)

图3 步长寻优Fig．3 Step optimization

1.4 控制流程

综合上述分析，给出多点激励正弦振动实数域控制算法的实现流程如图4所示，具体步骤如下：

第一步：根据各激励点的幅值和相位要求设定参考系数R(t)，初始化迭代条件：D0(t)=0m，C0(t)=0m，Z0(t)=Im。

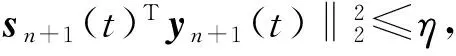
第四步：判断迭代次数是否超过规定最大次数限制，若超过结束特定频率的闭环控制，否则返回第二步，进入下一循环。

2 仿真与实验研究

2.1 仿真分析

下面利用Matlab软件对本文所提出的实数域控制算法的性能进行仿真分析。假设4点激励振动系统的频率响应矩阵为

正弦振动控制目标为：激励点1的参考幅值4.0 m/s2，参考相位60°；激励点2的参考幅值2.0 m/s2，参考相位120°；激励点3的参考幅值5.0 m/s2，参考相位30°；激励点4的参考幅值3.0 m/s2，参考相位90°。

采用Broyden算法按照式(22)修正驱动系数时，仿真得到多点激励振动系统的幅值响应如图5所示，相位响应如图6所示。可以看出，经过16次控制迭代后，激励点1的幅值和相位便分别趋近于4.0 m/s2和60°；激励点2的幅值和相位分别趋近于2.0 m/s2和120°，激励点3的幅值和相位便分别趋近于5.0 m/s2和30°；激励点4的幅值和相位分别趋近于3.0 m/s2和90°。仿真结果说明Broyden算法能够高效迭代得出满足系统响应要求的驱动系数。但图5中各激励点的幅值响应在迭代初始阶段出现了严重的过冲，激励点1的峰值达到70 m/s2，激励点2的峰值达到60 m/s2，激励点3的峰值达到85 m/s2，激励点4的峰值也已超过55 m/s2，在实际振动控制中容易造成系统的损坏。因此Broyden算法虽然理论效果明显，却并不适用于实际的振动控制。

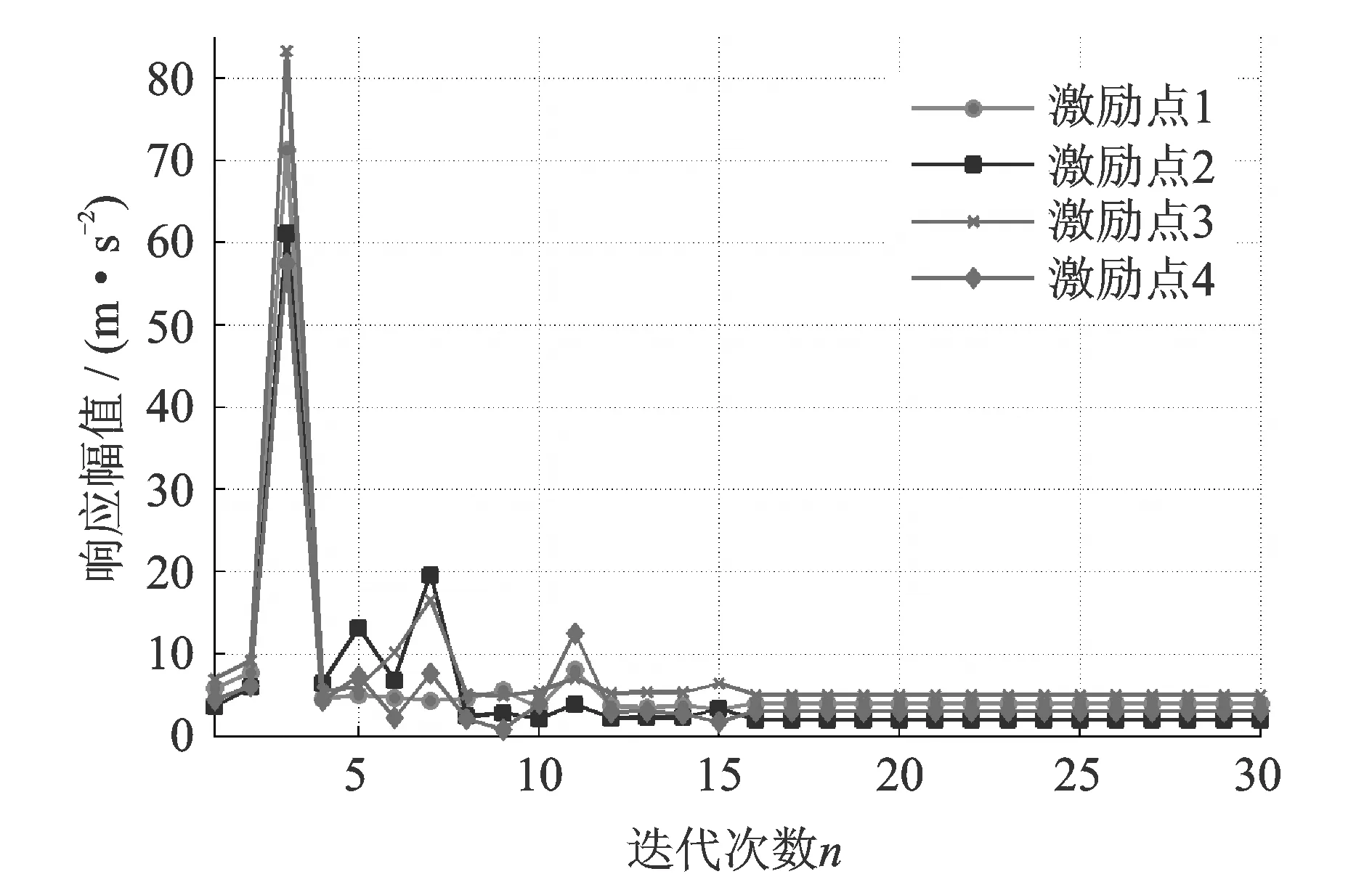
图5 Broyden算法的幅值响应Fig．5 Amplitude response of the Broyden method

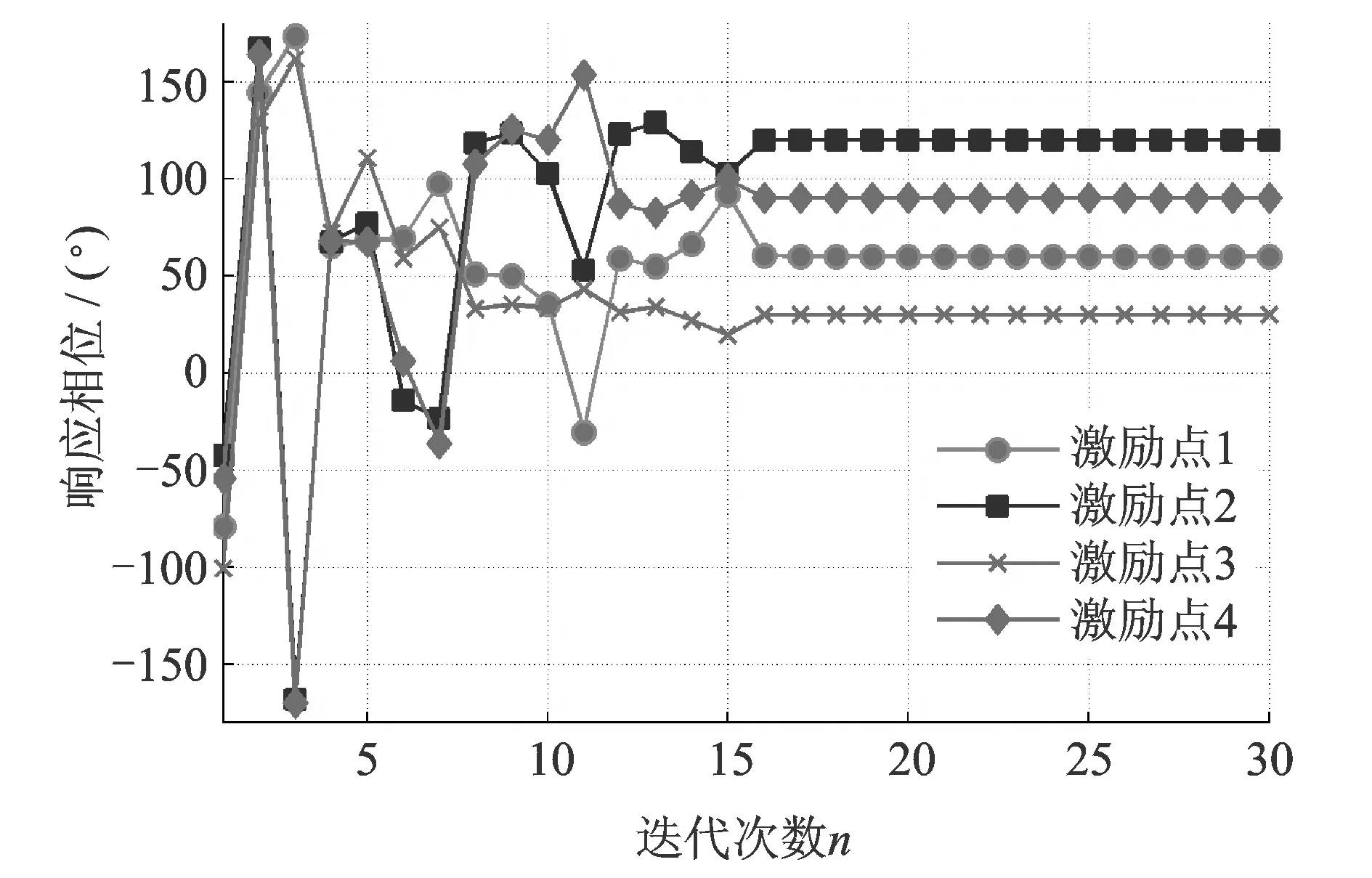
图6 Broyden算法的相位响应Fig．6 Phase response of the Broyden method

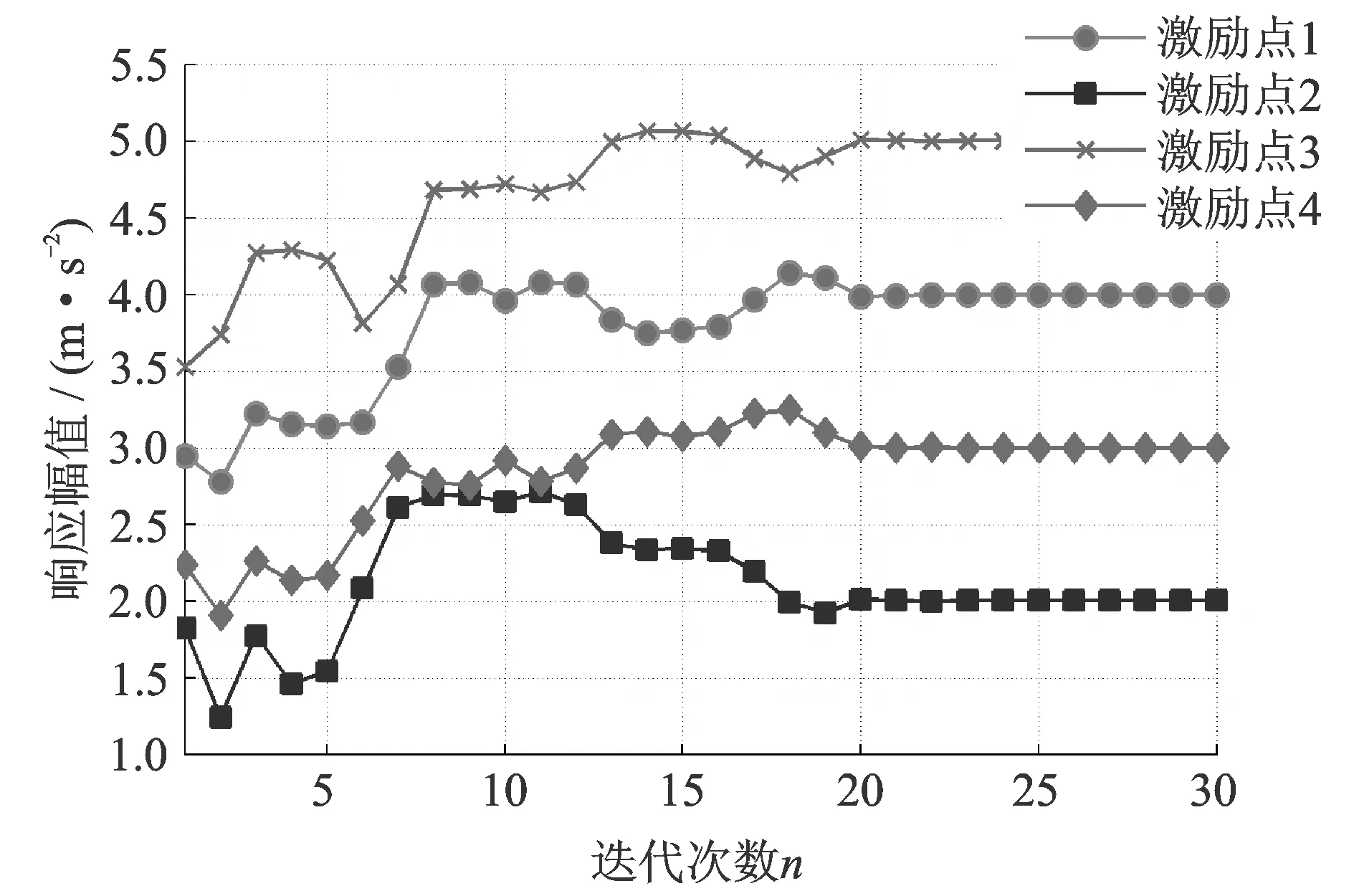
图7 步长寻优算法的幅值响应Fig．7 Amplitude response of the step optimization method

采用图4所示的包含步长寻优的实数域迭代算法进行控制时，仿真得到的幅值响应和相位响应分别如图7和8所示。可以看出，各激励点的幅值响应迭代初始阶段的过冲得到了明显改善，激励点1的过冲小于0.15 m/s2，激励点2的过冲小于0.70 m/s2，激励点3的过冲小于0.07 m/s2，激励点4的过冲小于0.25 m/s2。

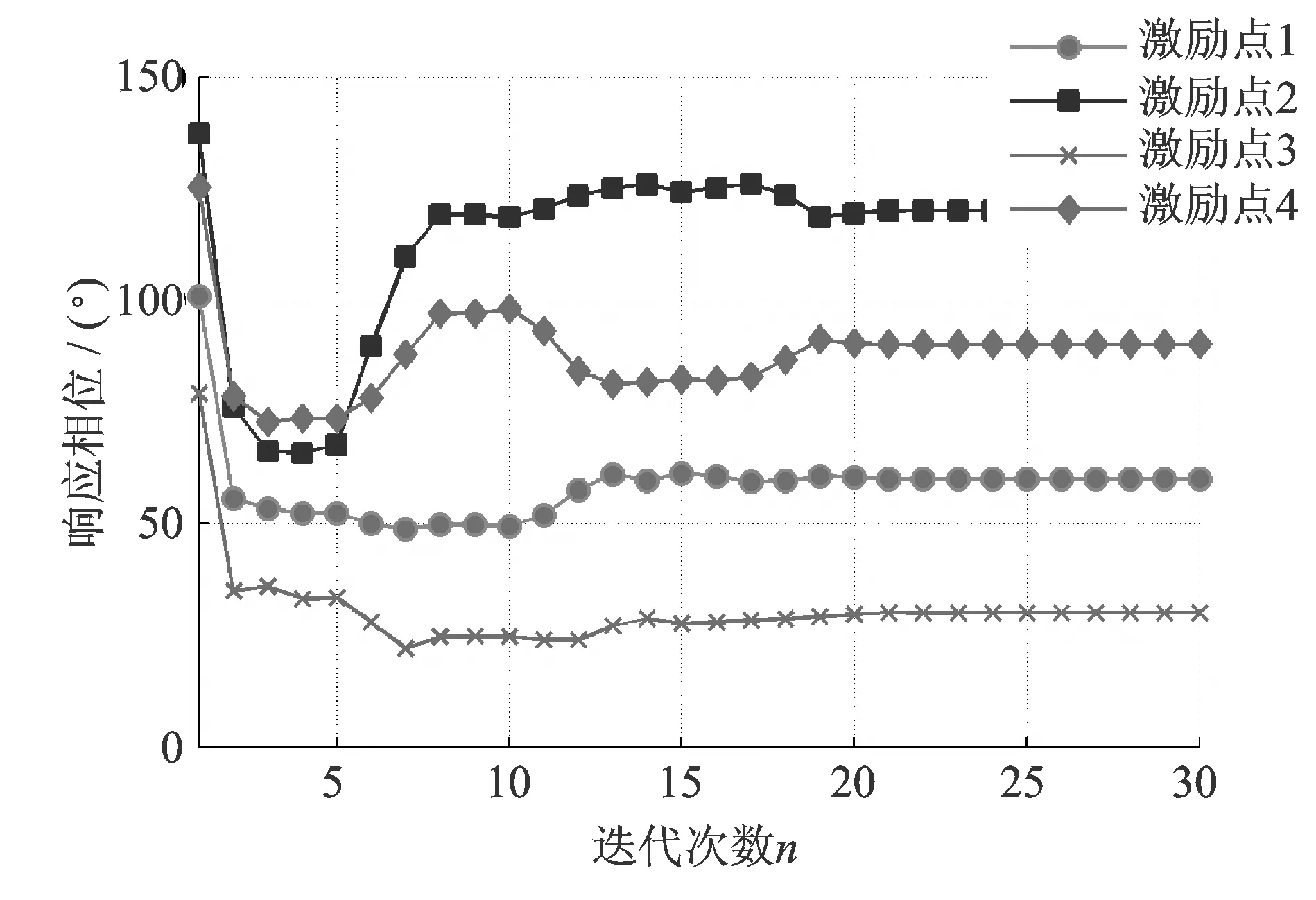
图8 步长寻优算法的相位响应Fig．8 Phase response of the step optimization method

误差系数的范数变化如图9所示，不断减小的误差系数范数说明驱动系数在迭代修正一直朝着目标方向进行，不存在振荡现象。如图7和8所示，经过20次迭代后，各激励点的幅值和相位也均趋近于各自的参考幅值和相位。仿真结果说明本文提出的实数域控制算法能够有效地完成多点激励正弦振动控制。

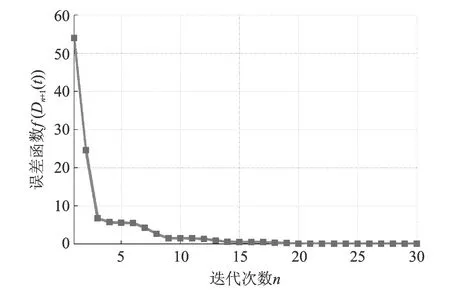
图9 步长寻优算法的误差范数Fig．9 Error norm of the step optimization method

2.2 实验验证

为了验证实数域控制算法的可行性，搭建两点激励振动系统进行试验研究，如图10所示。通过两个振动台同时激振三角横梁，横梁激励点附近安装加速度计实时测量振动大小，经电荷放大器转换成电压信号，振动控制器根据控制算法生成模拟电压信号，通过功率放大器驱动两振动台产生振动。

图10 两点激励振动系统Fig．10 Two exciters vibration system

首先，控制两振动台输出频率为320 Hz的正弦振动，其中激励点1的幅值为1.2g、相位为60°，激励点2的幅值为1.0g、相位为90°。采用图4所示的实数域迭代算法进行控制，得到的幅值和相位响应分别如图11和12所示。可以看出，经过15个迭代步长，激励点1的幅值和相位便分别趋近于1.2g和60°，迭代初始阶段没有出现幅值响应过冲；经过15个迭代步长激励点2的幅值和相位分别趋近于1.0g和90°，迭代初始阶段幅值响应的过冲小于0.2g。经过30个迭代步长两激励点幅值和相位的稳态误差均小于0.001g和0.1°，实验说明实数域迭代算法在320 Hz频率点具有良好的精度和速度，能有效避免振荡过冲现象。

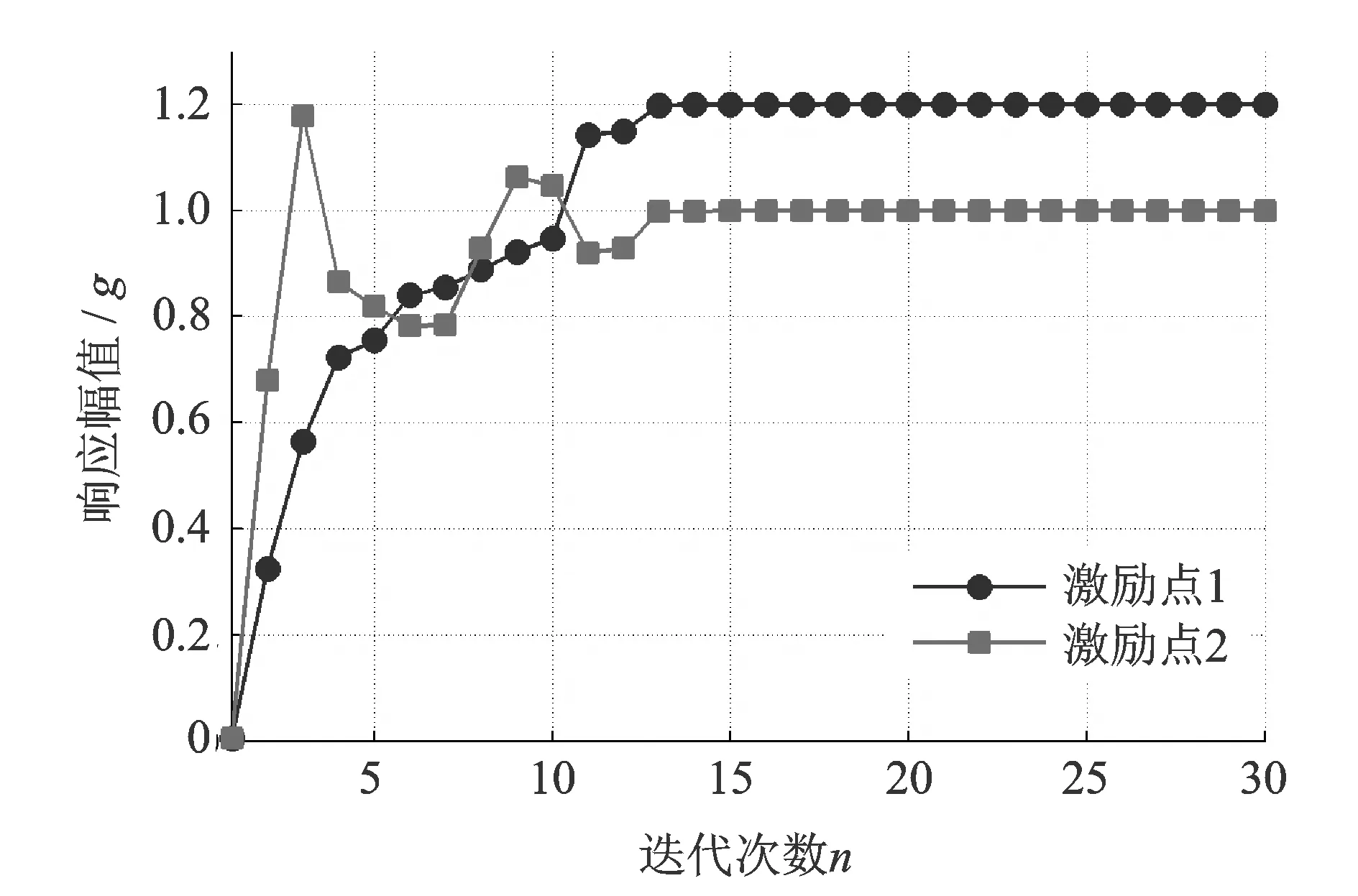
图11 320 Hz幅值响应Fig．11 Amplitude response at 320 Hz

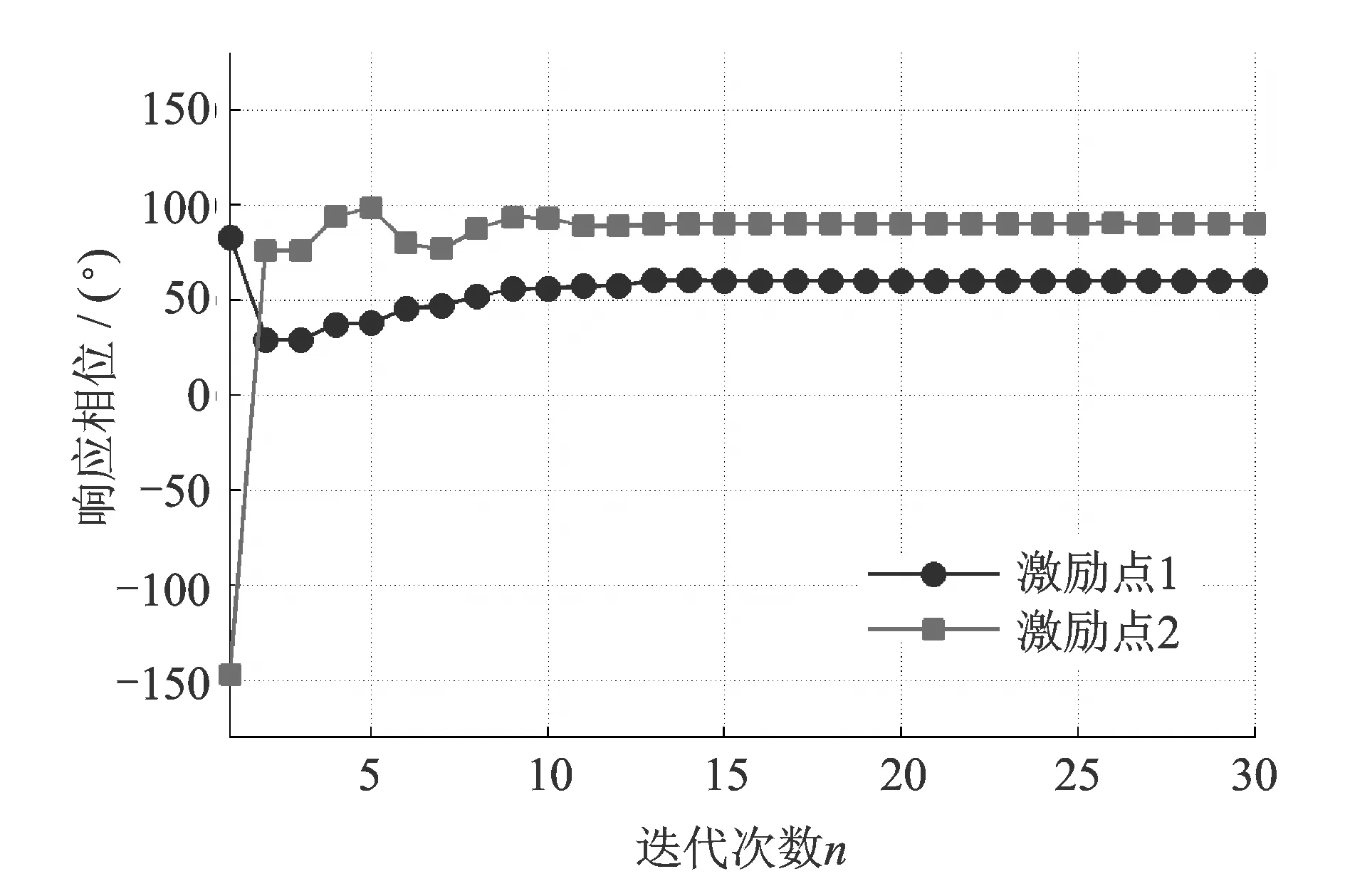
图12 320 Hz相位响应Fig．12 Phase response at 320 Hz

接下来，控制两振动台在40～2000 Hz的频率范围内振动，激励点1的参考幅值由上坡值(0.6～1.2g)和恒定加速度值(1.2g)组成，参考相位为60°，激励点2的参考幅值由上坡值(0.4～1.0g)和恒定加速度值(1.0g)组成，参考相位为90°。实验中经过30个迭代步长两激励点的幅值响应和相位响应分别如图13和14所示。可以看出，两激励点的幅值响应在上坡段和恒定段与参考值很接近，整个频率范围内幅值误差均小于0.01g，频率范围内两激励点的相位响应分别接近参考值60°和90°，误差小于1.5°。实验结果说明实数域控制算法在整个频率范围内具有良好的正弦振动控制能力。

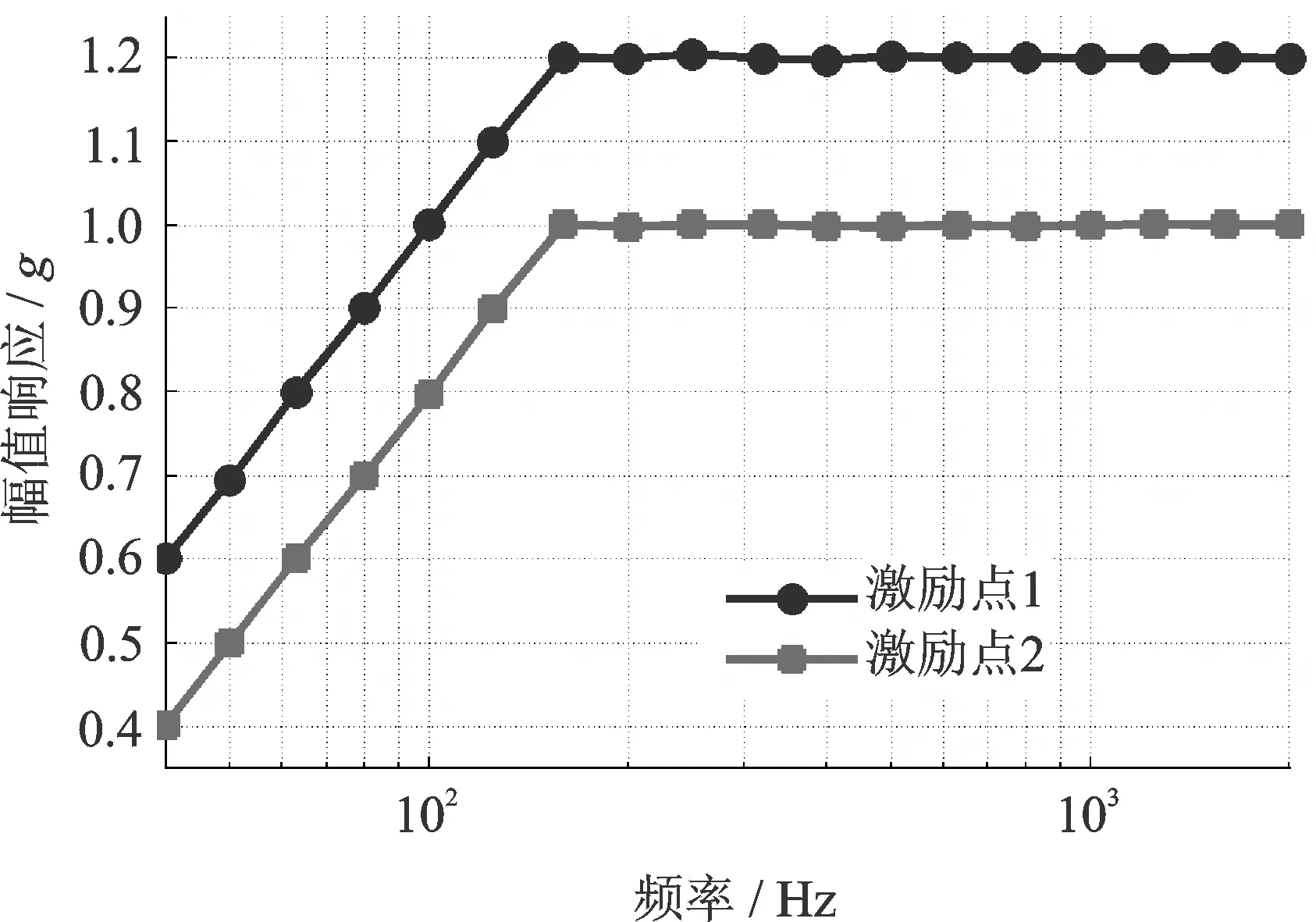
图13 频带范围内幅值响应Fig．13 Amplitude response in the frequency range

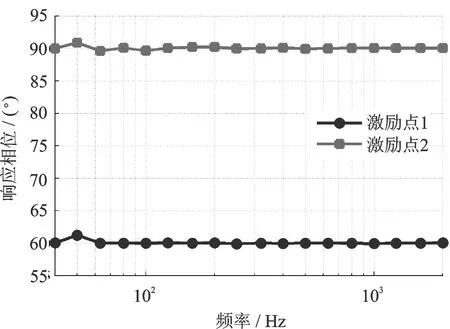
图14 频带范围内相位响应Fig．14 Phase response in the frequency range

3 结 论

本文通过建立多点激励正弦振动控制的实数域数学模型，推导出实数形式的阻抗矩阵更新公式，并确定了最优的迭代步长，提出多点激励正弦振动实数域控制算法的控制流程。仿真与实验结果表明，实数域控制算法具有快速的收敛速度，能够满足高精度的幅值和相位响应要求，且可以有效地避免控制过程中的振荡过冲现象。

[1] 夏益霖. 多轴振动环境试验的技术、设备和应用[J]. 导弹与航天运载技术, 1996, (6):52—59.

Xia Y L. The technology, equipment and application of multi-axis vibration environment testing [J]. Missiles and Space Vehicles, 1996, (6):52—59.

[2] Harman C. Historical development of high performance multi-axis vibration test systems[J]. Environmental Engineering, 2004, 17(1):40—41.

[3] 陈章位, 于慧君. 振动控制技术现状与进展[J]. 振动与冲击, 2009, 28(3):73—77.

Chen Z W, Yu H J. Existing state and development of vibration control technology [J]. Journal of Vibration and Shock, 2009, 28(3):73—77.

[4] Stroud R C, Hamma G A, Underwood M A, et al. A review of multiaxis/multiexciter vibration technology[J]. Sound and Vibration, 1996, 30(4):20—27.

[5] 齐华. 单轴多点激励正弦振动控制算法研究及其实现[D]. 北京：北京航空航天大学, 2001.

Qi H. The algorithm development and implementation for single-axis multi-exciter sine-wave vibration control[D]. Beijing:Beihang University, 2001.

[6] Fisher D. Theoretical and practical aspects of multiple-actuator shaker control[J]. 43rd Shock and Vibration Bulletin. 1973, 3:153—174.

[7] Hamma G A, Smith S, Stroud R C. Simulation of dynamic loads by multichannel digital control(computerized structural response prediction with application to multishaker testing)[C].Structures, Structural Dynamics and Materials Conference, 19th, Bethesda, Md. 1978: 422—430.

[8] Chen M, Wilson D. The new tri-axial shock and vibration test system at hill air force base[J]. Journal of IEST, 1989, 41(2):27—32.

[9] Flora L D, Gründling H A. Time domain sinusoidal acceleration controller for an electrodynamic shaker[J]. IET Control Theory Application, 2008, 2(12): 1044—1053.

[10]朱银龙, 陈怀海, 贺旭东, 等. 多输入多输出正弦振动试验控制系统算法研究及实现[J]. 振动工程学报, 2008, 21(1):62—65.

Zhu Y L, Chen H H, He X D, et al. Implementation of an algorithm for MIMO sinusoidal vibration test control system [J]. Journal of Vibration Engineering, 2008, 21(1):62—65.

[11]杨志东, 丛大成, 韩俊伟, 等. 基于拓展型准牛顿优化算法的单轴正弦扫频振动控制[J]. 振动与冲击, 2008, 27(3):99—103.

Yang Z D, Cong D C, Han J W, et al. Signle-axis swept sine vibration control using extended Quasi-Newton method [J].Journal of Vibration and Shock, 2008, 27(3):99—103.

[12]Underwood M A. Adaptive control method for multiexciter sine tests[Z]. United State Patents, 1994:5299459.

[13]Underwood M A, Keller T. Recent system developments for multi-actuator vibration control[J]. Sound and Vibration, 2001,35(10):16—23.

[14]陈家焱, 陈章位, 贺惠农, 等. 多点正弦振动试验控制系统最优控制策略研究[J]. 机械工程学报, 2012, 48(8):159—166.

Chen J Y, Chen Z W, He H N, et al. Optimum control strategy study for multi-exciter sine test control system [J]. Journal of Mechanical Engineering, 2012, 48(8):159—166.

[15]Yamauchi Y, Uchiyama Y, Ueno K, et al. Vibration control of multi-DOF excitation systems using modern control theory. Fatigue, 2000.

[16]李庆扬, 莫孜中, 祁力群. 非线性方程组的数值解法[M]. 北京：科学出版社, 1997.

Li Q Y, Mo Z Z, Qi L Q. Numerical Method for Non-linear Systems of Equations[M]. Beijing:Science Press, 1997.

Multi-exciter sine vibration control method in the real domain

LIUZhi-hua,CAIChen-guang,YUMei,XIAYan,LIJing-sheng

(National Institute of Mechology of China, Beijing 100029， China)

Multi-exciter sine vibration system has the ability to simulate more closely approximating real-world operating conditions which contributes to achieve the vibration characteristic of the test articles. The purpose of this paper is to present the real domain control method in order to avoid complex number operations in the traditional frequency domain iterative algorithm. The real domain mathematical model of multi-exciter sine vibration control is established. Broyden’s method is formulated to deduce the real-valued impedance matrix. The iterative step used to determine the updated driving signal is optimized. On this basis, control flow to implement the real domain control method is introduced. Simulation and experiment are carried out to verify the effectiveness of the proposed control method. The results demonstrate that the real domain control method has an advantage of efficient convergence, precise response and overshoot avoidance.

vibration control; multi-exciter; Quasi-Newton method; real domain

2016-01-23；

2016-04-25

国家自然科学基金青年基金资助项目(51605461)；中国博士后科学基金资助项目(2016M591229)；公益性行业科研专项项目(201410009)

TB535

1004-4523(2016)06-1003-08

10.16385/j.cnki.issn.1004-4523.2016.06.008

刘志华(1987—),男,助理研究员。电话:15201284652；E-mail:liuzhihua@nim.ac.cn