基础俯仰运动对风力机行星齿轮动力学特性的影响分析①

邱星辉， 韩勤锴, 褚福磊

(1.清华大学机械工程系， 北京 100084; 2.北京航天发射技术研究所， 北京 100076)

基础俯仰运动对风力机行星齿轮动力学特性的影响分析①

邱星辉1,2， 韩勤锴1, 褚福磊1

(1.清华大学机械工程系， 北京 100084; 2.北京航天发射技术研究所， 北京 100076)

由于塔架在风力作用下的弯曲振动，机舱会产生俯仰运动，进而对行星齿轮产生基础激励。从能量角度出发，考虑基础俯仰运动、轮齿脱啮和齿背啮合，通过第二类拉格朗日方程建立了基础俯仰运动下行星齿轮传动非线性弯-扭-轴耦合模型。与现有基础固定情况下的耦合模型相比，基础俯仰运动将引起附加阻尼、附加刚度和附加外激励，同时引起直齿轮平面运动与轴向运动的耦合。采用数值积分获得系统动态响应，评估轴向运动对系统动力学特性影响的大小，分析基础俯仰运动和齿圈支承刚度对行星齿轮动力学响应和均载特性的影响。结果表明，基础俯仰运动显著增大中心轮(行星架、齿圈和太阳轮)的横向振动；行星轮所受附加作用力不相同，运动对称性被破坏，系统出现不均载现象。当系统存在轮齿脱啮和齿背啮合时，增大齿圈支承刚度能显著改善均载特性，没有轮齿脱啮和齿背啮合时，均载系数随着齿圈支承刚度的增大而小幅增大。

行星齿轮； 基础俯仰运动； 能量法； 均载特性； 支承刚度

引 言

行星齿轮传动在结构上采用多个行星轮来分担载荷，形成功率分流，具有结构紧凑、体积小、传动比大和传动效率高等特点，在工程中得到广泛应用。关于行星齿轮的动力学建模和分析的研究较为广泛和深入[1]，模型类型不断发展，系统自由度和考虑因素不断增多，期望通过动力学分析为设计和振动控制提供理论依据。王世宇等[2]建立行星齿轮纯扭转集中参数模型研究了行星齿轮的固有特性。由于在齿轮运转过程中参与啮合的齿数发生变化，轮齿啮合刚度是周期时变的，成为齿轮传动的主要激励源。Wang[3]研究了时变刚度引起的行星齿轮参数稳定性。Parker等采用有限元法分析了轮齿脱啮引起的非线性现象，得到了抑制特定模态响应的相位调谐准则[4]，并对相位调谐的有效性进行了物理解释[5]。李同杰等[6]研究了行星齿轮间隙非线性引起的多值解及其稳定性。陆俊华[7]和Kahraman[8]分别研究了误差对行星齿轮均载特性的影响。Guo和Parker[9]考虑重力引起的轮齿双面啮合现象，研究了双面啮合与行星轮轴承载荷间的关系。Qiu等[10]研究了重力引起的不均载，着重分析了齿圈支承刚度对行星齿轮均载特性的影响。

上述研究在建模和分析过程中，没有考虑基础运动，即认为基础是不动的，仅关注行星齿轮传动本身的振动特性。但在实际运用中，基础运动是常见且不可避免的，例如风力机塔架弯曲振动产生的机舱运动。从单转子系统的研究可以发现，基础运动引起附加阻尼、附加刚度和附加外激励，显著改变单转子系统的动力学特性[11-12]。对风力机行星齿轮传动而言，风力机塔架在风载作用下的振动已有广泛研究，但相应基础运动对行星齿轮动态特性的影响及机理还不明了。因此，十分有必要建立适用于基础运动作用下行星齿轮传动的动力学模型，分析基础俯仰运动作用下行星齿轮的动态特性，进而评估基础俯仰运动对行星齿轮传动的影响。

本文从能量角度出发，考虑轮齿脱啮和齿背啮合，提出了基础俯仰运动下行星齿轮传动非线性弯-扭-轴耦合模型，并与基础固定情况下的模型进行对比，从模型上反映基础俯仰运动的影响。采用数值积分获得系统动态响应，评估齿轮轴向运动对系统的影响，细致分析基础俯仰运动和齿圈支撑刚度对行星齿轮传动动态响应、均载特性的影响。

1 系统动力学模型

图1所示为行星齿轮传动动力学模型的示意图，系统各构件均视为刚体，质量分别为mc,mr,ms,mj，转动惯量分别为Ic,Ir,Is,Ij，其中下标c,r,s,j(j=1,2,…,N，N为行星轮个数)分别代表行星架、太阳轮、齿圈和第j个行星轮。假定齿轮啮合变形用沿啮合线方向的等效弹簧表示，其中ksj为太阳轮与第j个行星轮啮合刚度，krj为齿圈与第j个行星轮啮合刚度。行星架、齿圈、太阳轮和行星轮横向支承刚度分别为kc,kr,ks,kp，轴向支承刚度为kcz,krz,ksz,kpz。中心构件扭转刚度为kcu,kru,ksu。作用在行星架和太阳轮上的转矩分别用Tc,Ts表示。

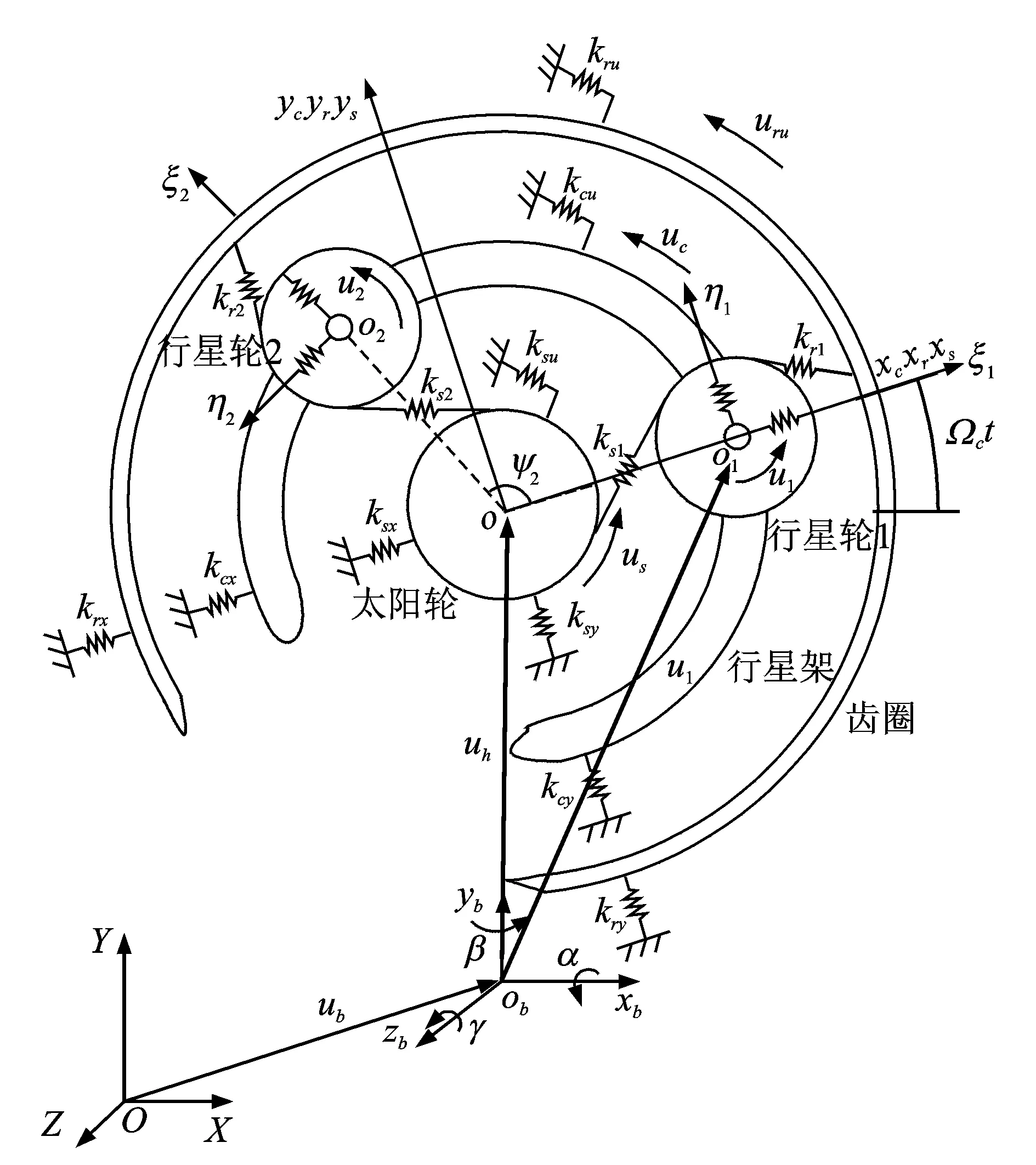
图1 基础运动下行星齿轮传动的动力学模型Fig.1 Dynamic model of the planetary gear under base motions

中心构件在局部坐标系oxyz中的运动为xl,yl,zl(l=c，r，s), 该坐标系以行星齿轮中心o为原点，其中心与第一个行星轮中心连线为x轴，齿轮平面内垂直于x方向为y轴。行星轮在局部坐标系ojξjηjzj中的运动用ξj,ηj和zj表示。这些局部坐标系以各行星轮中心oj为原点，ooj为ξ轴，齿轮平面内垂直于ξ方向为η轴。所有随体坐标系以行星架转速Ωc绕z轴匀速旋转。各构件的转动位移为uh=rhϑh(h=c,r,s,1,2,…,N)，其中ϑh为各构件转动角位移，rh为齿轮基圆半径。坐标系oxbybzb固定在基础上来描述基础运动，OXYZ为惯性坐标系。随体坐标系oxbybzb相对惯性坐标系的转动分别用α,β,γ表示，平动用ub表示。文中只考虑基础在惯性坐标系内的俯仰运动α，即β=0，γ=0，ub=0。

为统一坐标系的平移变换和旋转变换，引入齐次坐标表征构件在随体坐标系中的位置

(1)

(2)

通过齐次变换矩阵得到各构件质心在惯性坐标系中的位置ChR(h=c,r,s,1,2,…,N)：

ChR=Rot(x,α)Tran(uh)Rot(z,θh)Ch

(3)

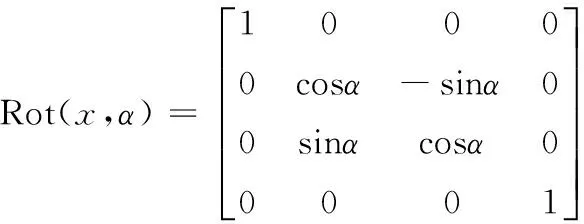
(4)

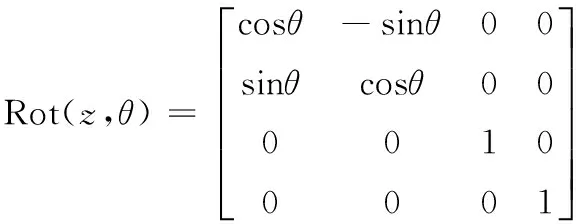
(5)

(6)

由于行星轮同时存在自转和公转运动，中心轮和行星轮的具体表达式略有不同：

θj=Ωct+φj

(7)

系统动能为

(8)

系统弹性势能包括轮齿啮合变形和支承弹性变形，基础运动不影响系统弹性势能的计算。轮齿传动面啮合变形为[9, 14]：

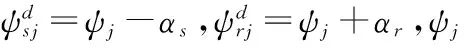
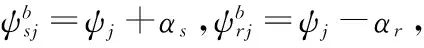
(13)

式中ba为齿侧间隙。行星轮轴承径向变形δjr和切向变形δjt为

(14)

2 动力学微分方程

取系统广义坐标为

(15)

通过第二类拉格朗日方程[13]，即可得到系统运动微分方程

(16)

行星架运动微分方程为：

(17)

齿圈运动微分方程为：

(18)

太阳轮运动微分方程为：

(19)

行星轮运动微分方程为：

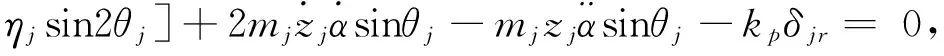
(20)

引入阻尼项，将以上4(N+3)个方程写成矩阵形式为

(21)

其中M为质量矩阵，G为反对称陀螺矩阵，KΩ为向心刚度矩阵，Kmd为传动面啮合刚度矩阵，Kmb为齿背啮合刚度矩阵，KB为轴承刚度矩阵，F为作用在行星齿轮上的扭矩载荷，Fmb为齿背啮合产生的非线性外激励力。C=(V-1)Tdiag(2ξnωn)V-1为通过模态阻尼比引入的阻尼矩阵，其中ξn(n=1,2,…,4(N+3))为模态阻尼比，ωn为不考虑基础俯仰运动和啮合刚度变化时的系统固有频率，V为正则振型矩阵。上述矩阵均与基础固定情况下行星齿轮模型[10]一致。

基础俯仰运动的影响为引起附加阻尼Cb、附加刚度Kb和附加外激励Fb，具体表达式如下：

(22)

Kbh=mh·

(23)

(24)

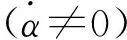
3 算例分析

图1所示的行星传动采用不同的固联模式和自由度分配可以有完全不同的传动模式，但其动力学建模与分析方法相同，只是存在动力学参数取值差异。本节动力学分析以美国可再生能源实验室(NREL)550 kW风力机行星齿轮参数为基础[16]，主要模拟参数如表1所示。风力机行星齿轮传动是增速齿轮传动，以行星架为输入端，太阳轮为输出端，齿轮箱采用柔性支承与机舱底座相连。假定基础俯仰运动的形式为α=Bsin2πfbt。由表1可知，示例行星齿轮系统有N=3个行星轮且均匀分布，中心轮齿数能被行星轮个数整除，故各行星轮同相啮合，啮合刚度完全相同，其傅里叶级数展开式为

(j=1,2,…,N)

(25)

对动力学方程(21)采用变步长龙格库塔数值积分求得系统动态响应。图2为基础俯仰运动B=15°，fb=5 Hz情况下行星架和行星轮1的振动响应。与不考虑基础俯仰运动时中心轮横向振动响应可忽略不计的情况相比，基础俯仰运动显著增大中心轮的横向振动，齿轮轴向存在稳定的周期振动。

表1 示例行星齿轮传动主要模拟参数

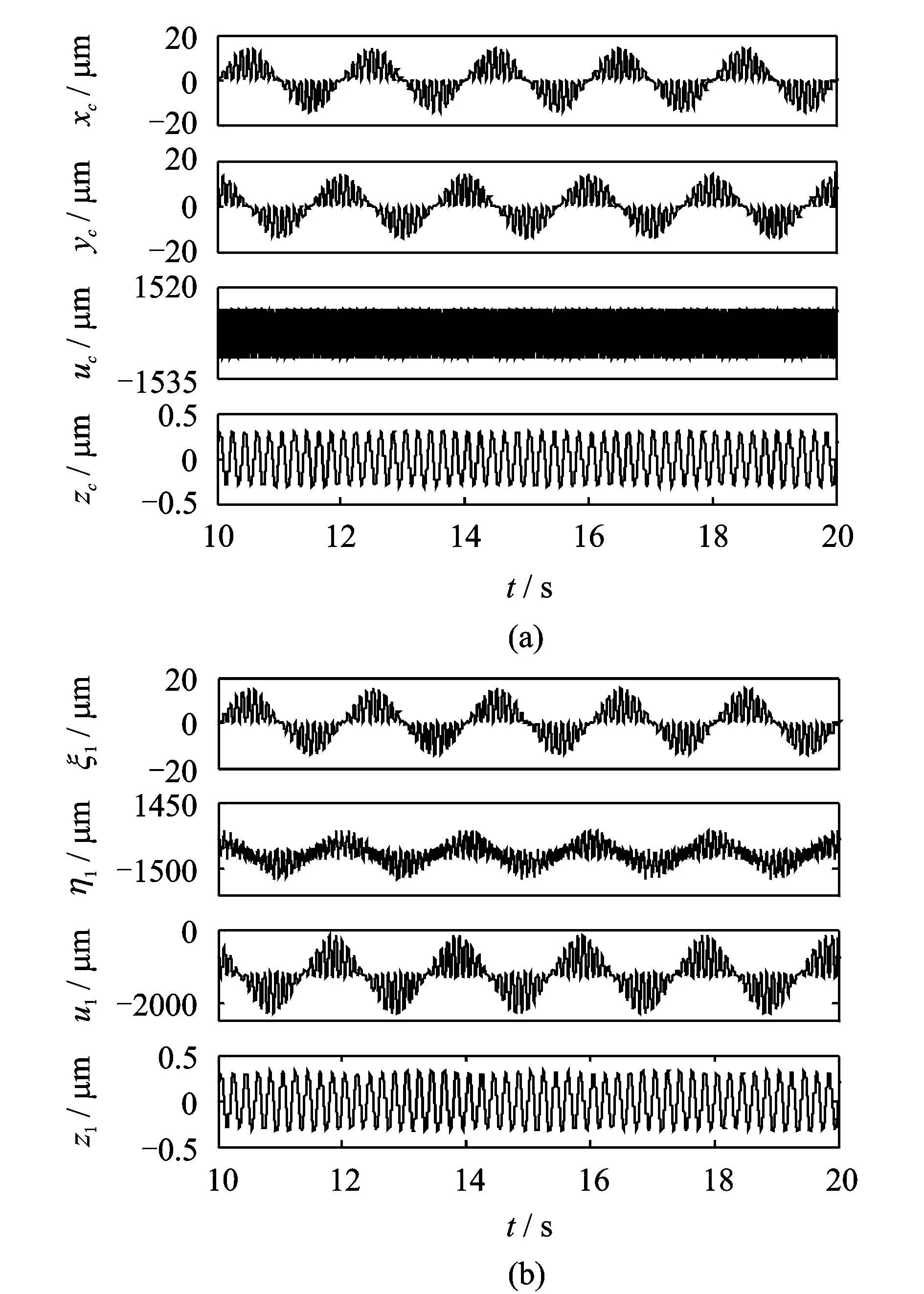
图2 存在基础俯仰运动B=15°，fb=5 Hz情况下行星架和行星轮1的振动位移Fig.2 Vibration displacements of the carrier and planet 1 with pitching base motion B=15°，fb=5 Hz

基础俯仰运动增大中心轮横向振动这一现象可以从行星齿轮的模态进行很好的解释。由于行星齿轮结构对称性，其固有特性具有很好的规律性[10, 14, 17]。表1中示例行星齿轮的模态可以分为扭转模态、平移模态和轴向模态：扭转模态中，中心轮只有扭转运动，各行星轮运动相同；平移模态中，中心轮只有平动，行星轮运动不相同；轴向模态中，行星齿轮只有轴向运动。当不考虑基础俯仰运动时，系统激励源为刚度激励和外部扭矩；当行星轮均布且同相啮合时，只有扭转模态被激起，平移模态响应被抑制[4-5]，因而中心轮几乎没有横向振动。考虑基础俯仰运动后，由于附加刚度和附加外激励力的作用，平移模态被激起，中心轮横向振动响应显著增大。

对于直齿轮，轮齿动态啮合力作用在齿轮平面内，在轴向方向并无分量，因而在分析直齿轮动态响应时通常不考虑齿轮轴向运动[8-10]。基础俯仰运动引起的平面运动与轴向运动耦合效应的强弱可以通过对比考不考虑轴向运动情况下的振动幅度来衡量。如图3所示，当基础运动频率fb从0增大到10 Hz时，齿轮横向、轴向运动和轮齿啮合变形均随之增大，但轴向运动远小于横向运动。两种情况下得到的齿轮横向振动和齿轮啮合变形差别可忽略不计，因此当基础俯仰运动频率较低或幅度较小时，可以忽略齿轮轴向运动。

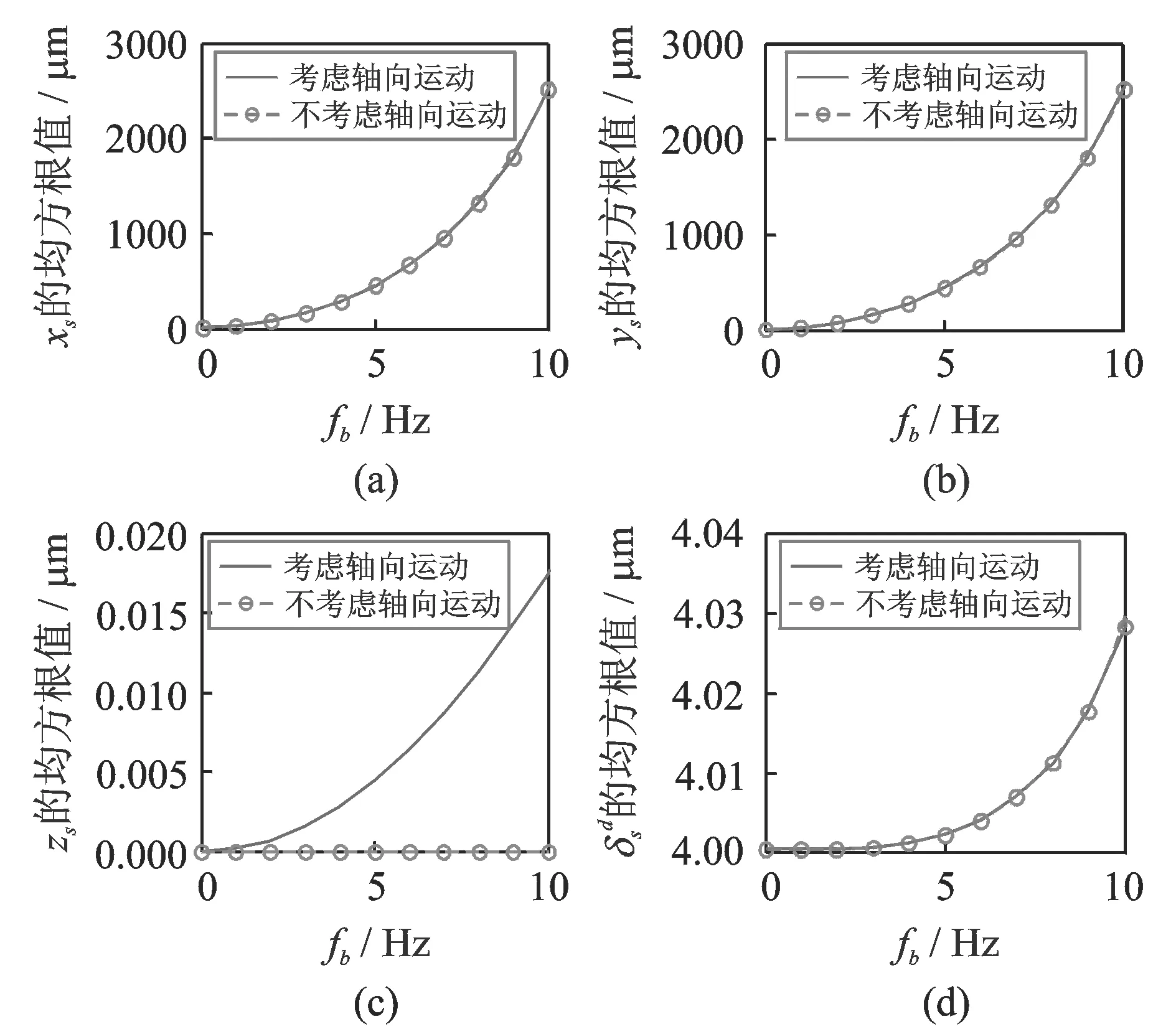
图3 轴向运动对系统振动特性的影响Fig.3 Influence of axial motions on the dynamic behaviors of the planetary gear

4 参数影响分析

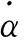
不同基础运动频率下太阳轮-行星轮啮合变形如图4所示。无基础运动时，各行星轮结构对称且承受相同的激励，示例行星齿轮的扭转模态被激起，而在扭转模态中各行星轮运动完全相同，此时系统完全均载(图4(a))。当B=15°，fb=5 Hz时，基础俯仰运动引起的附加刚度和附加外激励不相同，且各行星轮附加外激励不关于行星齿轮中心对称，行星齿轮受力对称性被破坏，各行星轮运动出现差异，但差异不大(图4(b))，且轮齿啮合未出现轮齿脱啮和齿背啮合现象。当fb增大到13 Hz时，如图4(c),(d)所示，系统出现轮齿脱啮和齿背啮合现象，行星轮运动差异明显，不均载现象严重。

行星齿轮的均载情况可采用均载系数来定量衡量[10]

KLS(t)= max{fpj(t)}|j/mean{mean[fpj(t)]|j}|t

(26)

式中fpj(t)为行星轮轴承承受的动态载荷。由于式(26)为时间函数，本文取max[KLS(t)]作为均载指标。理想情况下，载荷在行星轮间均匀分布，均载系数为1。

在图4所示的三种基础俯仰运动条件下，随着基础运动频率的增大，行星齿轮会出现轮齿脱啮和齿背啮合，系统从线性时变系统转变为非线性时变系统，中心轮的运动轨迹同样会发生显著变化。如图5(a)所示，当没有基础运动时，行星架无横向振动，质心运动轨迹为一点；当基础运动频率较小时(fb=5 Hz)，行星架横向振动增大，质心运动轨迹为花瓣形，如图5(b)所示；当基础运动频率增大到13 Hz时，行星架横向振动显著增大，且其质心运动轨迹变得十分复杂。

在风力机齿轮传动中，箱体与机舱的连接通常采用柔性支承，在基础存在俯仰运动时齿圈支承刚度kr对行星齿轮动态响应影响如图6所示。显然，增大齿圈支承刚度能显著减小中心轮的横向振动，但对中心轮扭转振动的影响与基础俯仰运动导致的齿轮啮合状态有关：如图6(a)所示，当系统未出现轮齿脱啮和齿背啮合时，增大齿圈支承刚度对中心轮扭转振动的影响非常小；存在轮齿脱啮和齿背啮合时，增大齿圈支承刚度能显著减小中心轮的扭转振动，如图6(b)所示。

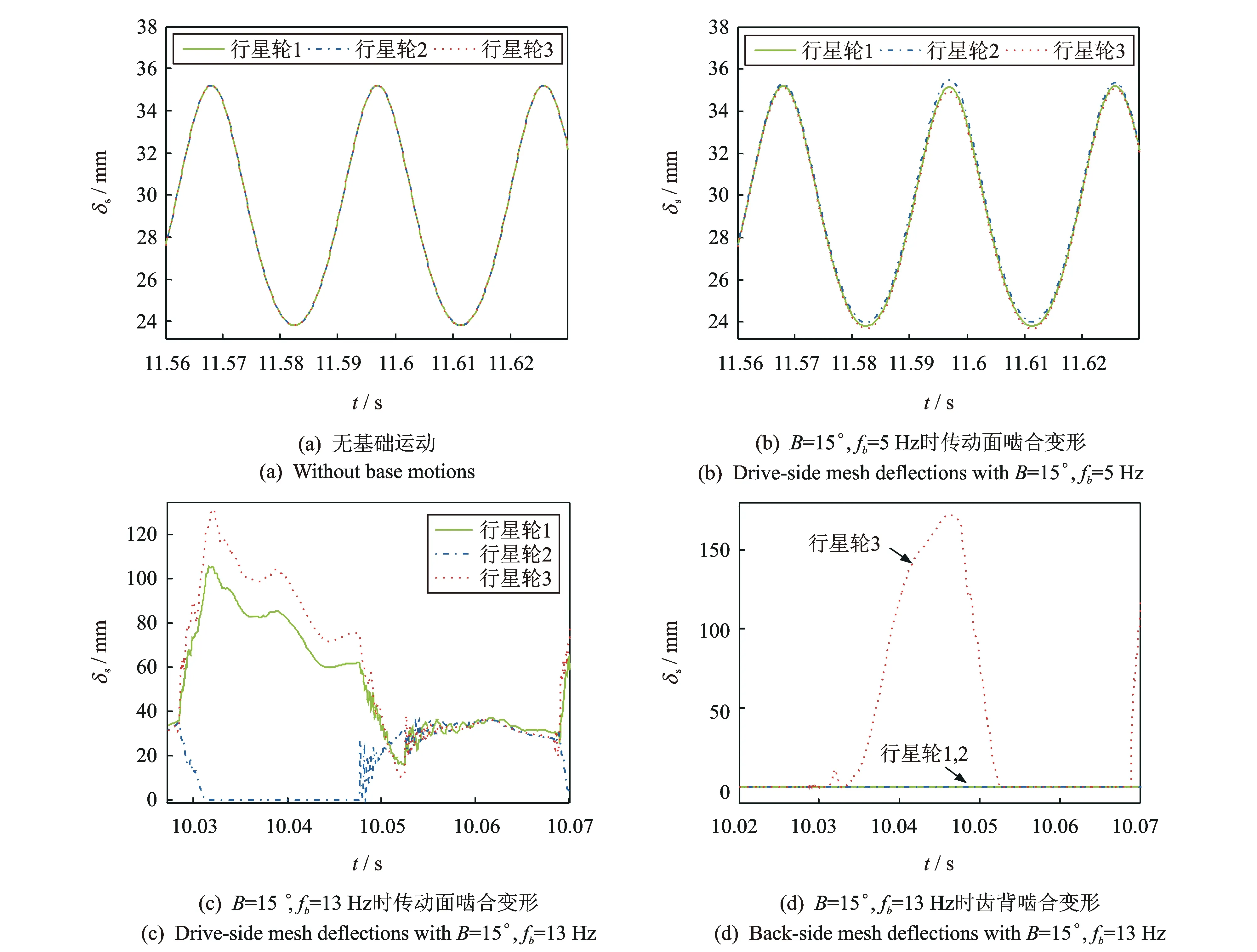
图4 不同基础运动频率下太阳轮-行星轮啮合变形Fig.4 Sun-planet mesh deflections with different pitching base motion frequency

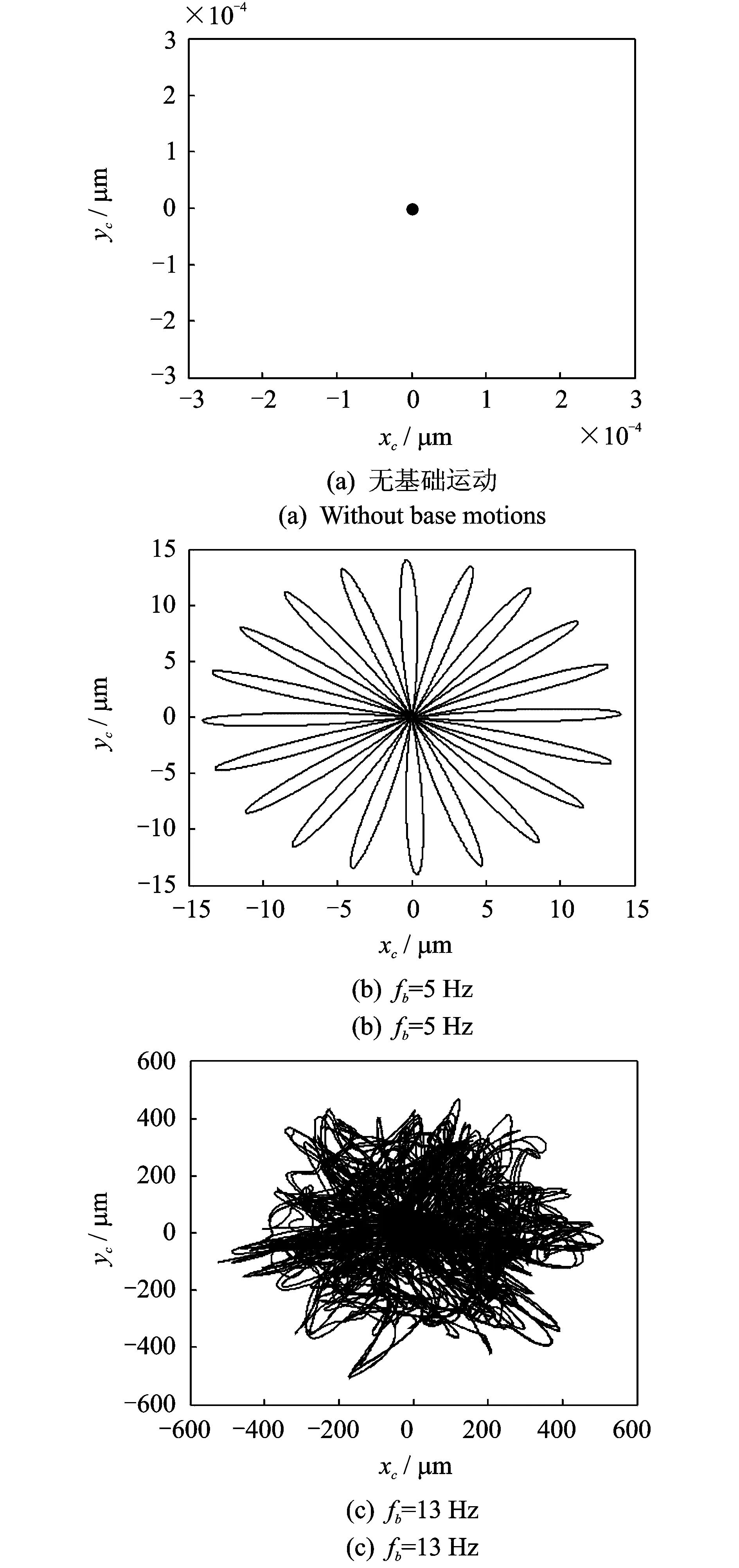
图5 不同基础运动频率下行星架相图Fig.5 Phase diagram of the carrier under different base frequency

齿圈支承刚度对行星齿轮均载特性的影响如图7所示。同样，齿圈支承刚度对均载特性的影响也与基础俯仰运动造成的啮合状态有关：如图7(a)所示，基础俯仰运动未引起脱啮和齿背啮合时，随着支承刚度的增大，均载系数增大，但增幅很小；如图7(b)所示，当基础俯仰运动引起脱啮和齿背啮合时，增大该支承刚度能显著减小均载系数，当其增大到一定值后，轮齿脱啮和齿背啮合被抑制，均载系数又呈现小幅增大的趋势。

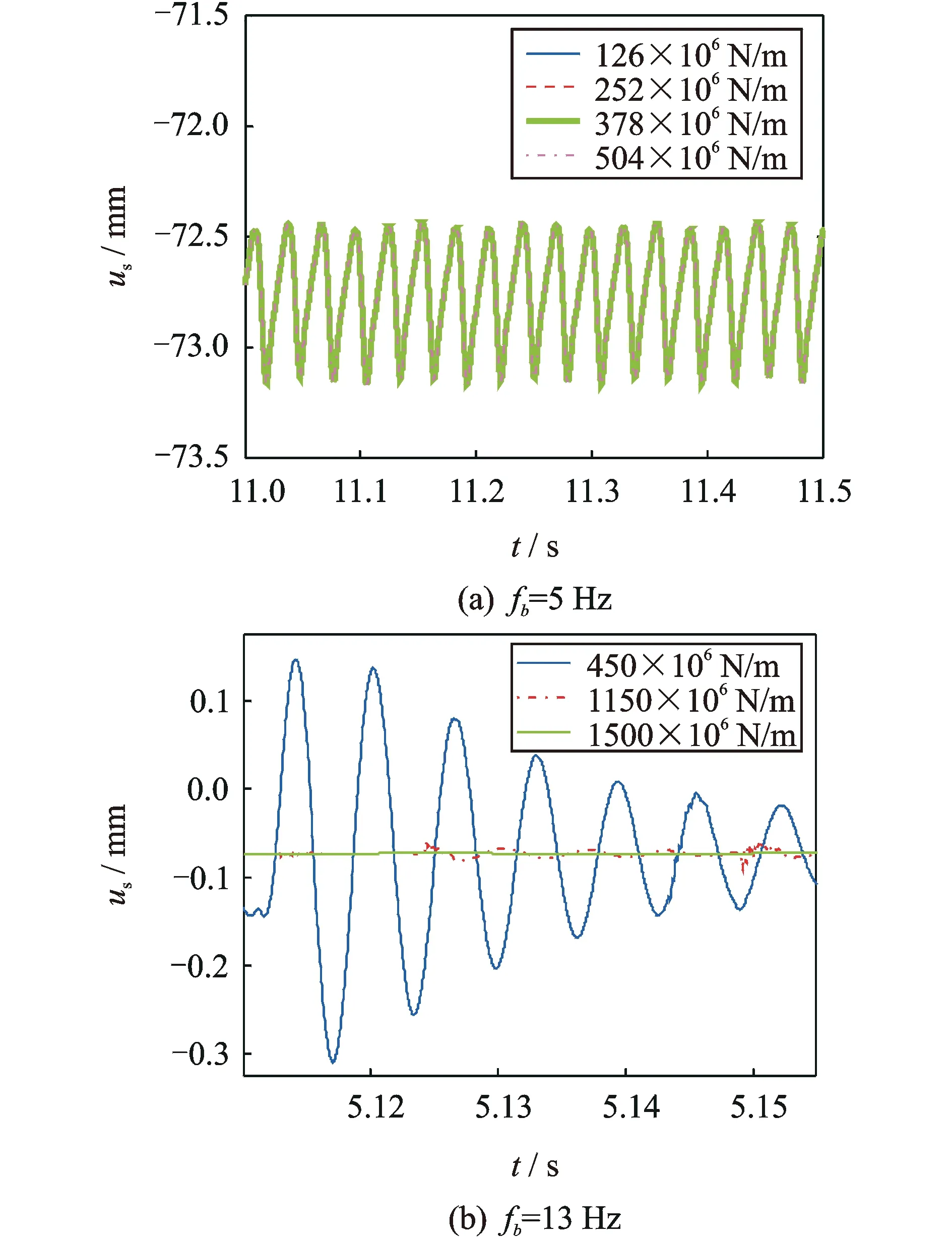
图6 齿圈支承刚度kr对太阳轮扭转振动的影响Fig.6 Influence of ring support stiffness kr on rotational vibration of the sun

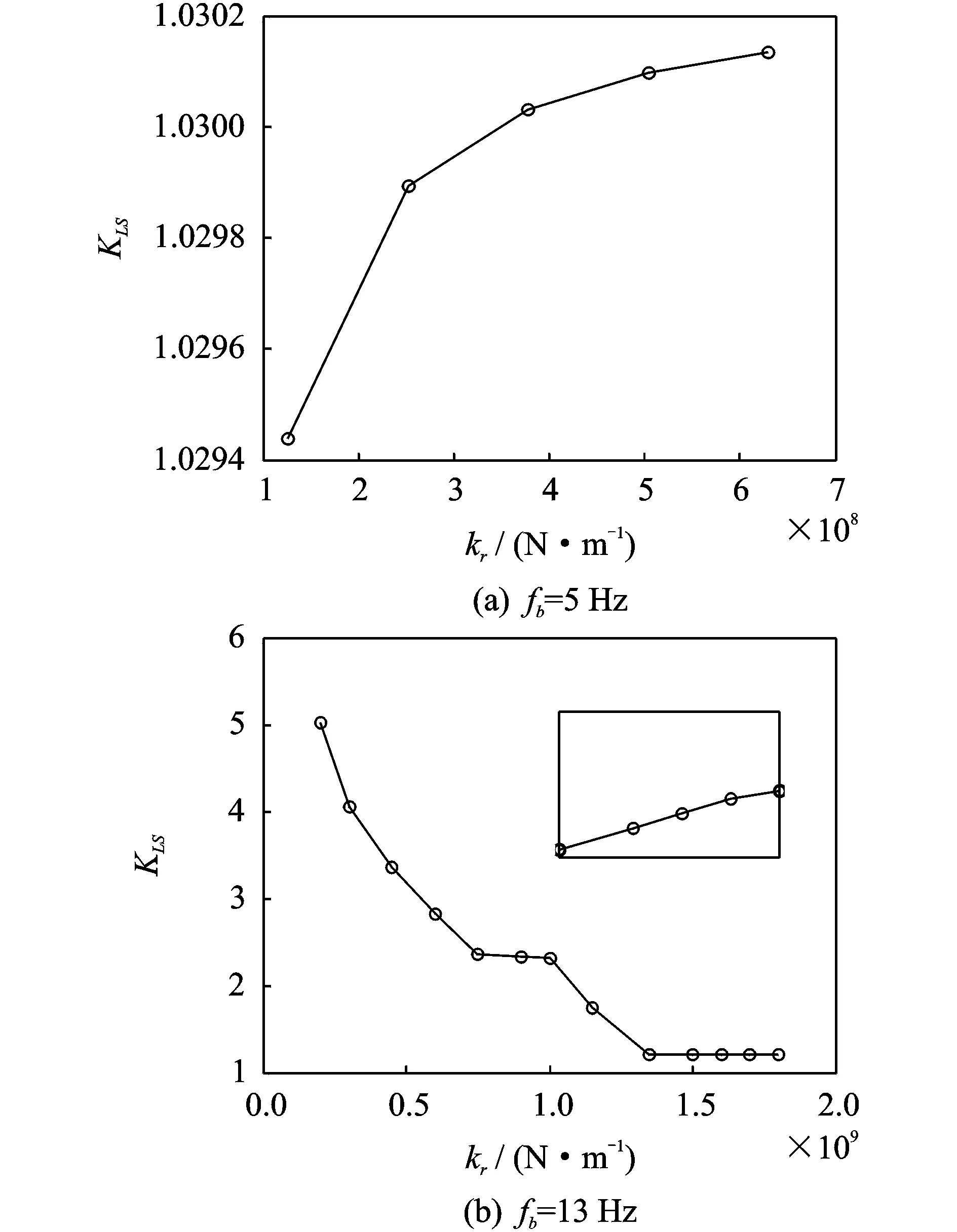
图7 基础俯仰运动下齿圈支承刚度kr对均载系数的影响Fig.7 Influence of ring support stiffness kr on load sharing factor with pitching base motion

5 结 论

本文从能量角度出发，通过拉格朗日方程建立了基础俯仰运动下行星齿轮传动弯-扭-轴非线性耦合模型，并与基础固定情况下的行星齿轮传动模型进行了对比。通过变步长龙格库塔数值积分获得系统动态响应，评估了齿轮轴向运动对系统动态特性的影响，分析了基础俯仰运动参数和齿圈横向支承刚度对行星齿轮动态响应和均载特性的影响规律。主要结论如下：

(1) 动态基础俯仰运动会产生附加阻尼、附加刚度和附加外激励力，并引起齿轮轴向运动和平面运动的耦合。

(2) 基础俯仰运动显著增大中心轮的横向振动，破坏行星齿轮的受力对称性，各行星轮运动出现差异，导致系统出现不均载。

(3) 当基础俯仰运动引起轮齿脱啮和齿背啮合时，增大齿圈支承刚度能显著改善系统均载特性；当未出现轮齿脱啮和齿背啮合时，不均载随着齿圈支承刚度的增大而小幅增大。

[1] 邱星辉，韩勤锴，褚福磊. 风力机行星齿轮传动系统动力学研究综述[J]. 机械工程学报，2014，50(11)：23—36.

Qiu Xinghui, Han Qinkai, Chu Fulei. Review on dynamic analysis of wind turbine geared transmission systems[J]. Journal of Mechanical Engineering, 2014,50(11)：23—36.

[2] 王世宇，宋轶民，沈兆光,等.行星传动系统的固有特性及模态跃迁研究[J]. 振动工程学报，2005，18(4)：412—417.

Wang Shiyu， Song Yimin， Shen Zhaoguang, et al. Research on natural characteristics and loci veering of planetary gear transmissions[J]. Journal of Vibration Engineering， 2005，18(4)：412—417.

[3] Wang S Y, Sinha S C. Parametric instability in a gear train system due to stiffness variation[C]. ASME IDETC/CIE 2013, Portland, Oregon, USA, 2013.

[4] Parker R G， Agashe V， Vijayakar S M. Dynamic response of a planetary gear system using a finite element/contact mechanics model[J]. Journal of Mechanical Design， 2000，122：304—310.

[5] Parker R G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J]. Journal of Sound and Vibration, 2000,236:561—573.

[6] 李同杰，朱如鹏，鲍和云,等.行星齿轮传动系的周期运动及其稳定性[J].振动工程学报，2013，26(6)：815—822.

Li Tongjie， Zhu Rupeng， Bao Heyun, et al. Coexisting periodic solutions and their stability of a nonlinear planetary gear train[J]. Journal of Vibration Engineering， 2013，26(6)：815—822.

[7] 陆俊华，朱如鹏，靳广虎. 行星传动动态均载特性分析[J]. 机械工程学报，2009，45(5)：85—90.

Lu Junhua， Zhu Rupeng， Jin Guanghu. Analysis of dynamic load sharing behavior in planetary gearing[J]. Journal of Mechanical Engineering， 2009，45(5)：85—90.

[8] Kahraman A. Load sharing characteristics of planetary transmissions[J]. Mech. Mach. Theory， 1994，29(8)：1151—1165.

[9] Guo Y， Parker R G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity[J]. European Journal of Mechanics A—Solid， 2010，29：1022—1033.

[10]Qiu X， Han Q， Chu F. Load-sharing characteristics of planetary gear transmission in horizontal-axis wind turbines[J]. Mech. Mach. Theory， 2015，92：391—406.

[11]Duchemin M， Berlioz A， Ferraris G. Dynamic behavior and stability of a rotor under base excitation[J]. Transactions of the ASME Journal of Vibration and Acoustics，2006，128：576—585.

[12]Han Q，Chu F. Dynamic response of cracked rotor-bearing system under time-dependent base movements[J]. Journal of Sound and Vibration，2013，332(25)：6847—6870.

[13]张义民. 机械振动[M]. 北京: 清华大学出版社，2007.

Zhang Yimin. Mechanical Vibration[M]. Beijing: Tsinghua University Press， 2007.

[14]Lin J， Parker R G. Analytical characterization of the unique properties of planetary gear free vibration[J]. Journal of Vibration and Acoustics， 1999，121：316—321.

[15]Guo Y， Parker R G. Analytical determination of back-side contact gear mesh stiffness[J]. Mechanism and Machine Theory, 2014，78：263—271.

[16]Guo Y, Keller J, Parker R G. Dynamic analysis of wind turbine planetary gears using an extended harmonic balance approach[C]. International Conference on Noise and Vibration Engineering， 2012，Leuven，Belgium. 1—18.

[17]王世宇，基于相位调谐的直齿行星齿轮传动动力学理论与实验研究[D].天津：天津大学,2005.

Wang Shiyu. Theoretical and experimental research on the dynamics of spur planetary gear based on meshing phase tuning[D]. Tianjin：Tianjin University，2005.

Influence of pitching base motion on the planetary gear in wind turbines

QIUXing-hui1,2,HANQin-kai1,CHUFu-lei1

(1.Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China;
2.Beijing Institute of Space Launch Technology, Beijing 100076, China)

Because of the tower vibration induced by wind load, the cabin will experience pitching motion, which causes pitching base motion to the planetary gear. Considering pitching base motion, tooth separation and back-side contact, a rotational-translational-axial model of the planetary gear under pitching base motion is presented through the Lagrange equation of the second kind. Compared with the traditional model, pitching base motion induces additional damping, stiffness and external excitation, and coupling between axial motion and in-plane motions of the gear. Through numerical integration, the dynamic response is obtained. The influence of axial motions on the planetary gear is evaluated, and the influence of base motion and ring support stiffness on the dynamic response and load sharing is investigated. Pitching base motion significantly increases the transverse vibrations of the central components (carrier, ring, sun). Additional forces on planets are not identical, and thus the movement symmetry is destroyed. With the existence of tooth separation and back-side contact, increasing the ring support stiffness can significantly improve the load sharing condition. Without tooth separation and back-side contact, load sharing factor increases slightly with the ring support stiffness.

planetary gear; pitching base motion; energy method; load sharing; support stiffness

2015-11-11；

2016-04-09

国家自然科学基金资助项目(51335006); 北京市自然科学基金资助项目(3131002)

TH132.425； TH113

1004-4523(2016)06-0945-09

10.16385/j.cnki.issn.1004-4523.2016.06.001

邱星辉(1988—)，女，博士。电话：18810644220；E-mail：qxhtt123@sina.com