多孔介质矩形薄板的精细积分模型①

向 宇, 蒋红华, 袁丽芸, 陆 静

(1.广西科技大学汽车与交通学院， 广西 柳州 545006；2.广西汽车零部件与整车技术重点实验室(广西科技大学)， 广西 柳州 545006)

多孔介质矩形薄板的精细积分模型①

向 宇1,2, 蒋红华1,2, 袁丽芸1,2, 陆 静1,2

(1.广西科技大学汽车与交通学院， 广西 柳州 545006；2.广西汽车零部件与整车技术重点实验室(广西科技大学)， 广西 柳州 545006)

基于三维Biot理论和弹性薄板理论，考虑多孔介质薄板骨架与流体的耦合作用，导出了多孔介质矩形薄板在谐激励作用下的一阶常微分矩阵方程。利用齐次扩容精细积分方法，对两对边简支矩形薄板在均布荷载和集中荷载两种情况下的弯曲振动问题进行了求解，对比经典算例，验证了所建模型的可行性和有效性。相对于数值方法，本文提出的方法适用于中高频段的分析计算。

多孔介质矩形薄板; 吸声; Biot理论; 齐次扩容精细积分法

引 言

由于多孔介质材料具有出色的吸声、吸能特性，广泛应用于交通运输、土木工程等工程领域。因此，对其进行声振性能研究，尤其是对多孔介质板壳结构的声振特性分析具有重要意义。1956年，Biot提出饱和含流多孔介质振动和声传播理论，创建了多孔介质材料动力学分析的经典理论[1]。由于涉及的材料参数太复杂且含义抽象，国内外学者对经典Biot理论进行了简化和修改，提出了更易理解和实际应用的修正Biot理论[2]，并建立了相应的多孔介质板壳结构的解析模型。Theodorakooulos等采用Fourier级数展开的方法求解了四边简支多孔介质薄板的弯曲振动问题[3]，并分析了惯性、孔隙率等对振动响应的影响。在此基础上，Leclaire建立了一种求解四边简支和固支多孔介质薄板更为简单的模型[4-5]。但是，由于仅考虑了流体相对于固体骨架的法向相对运动，他们的模型只适用于含轻质流体多孔介质薄板的低频声振分析。基于修正的Biot理论，陈卫松[6]和宁景锋等[7]研究了含多孔材料层合板的隔声性能和吸声性能，讨论了厚度、孔隙率等参数对结构声学特性的影响。目前，多孔介质薄板的理论模型中均忽略或部分忽略了多孔骨架与流体的相互作用，且解析求解方法仅能处理形状规则和有限的简单边界条件。为克服这一困难，数值解法在多孔介质结构的声振特性分析中得到了较大发展。Atalla等人通过用声压来描述流体位移，建立了一种基于混合位移-声压方程的多孔介质结构有限元模型[8]，相对于文献[9]中基于经典Biot理论建立的位移-流体模型，该模型的节点自由度从6个减少为4个，大大降低了计算规模。Batifol等在文献[8]的基础上，进一步推导了Comsol软件环境下多孔介质混合位移-声压方程的表达式，建立了压电/多孔介质弹性夹芯板的多物理场混合有限元模型[10]。2011年，胡莹等采用Batifol的方法对含多孔材料多层板的声学性能进行了研究[11]。然而，由于低阶形函数的单元离散和插值，使有限元等数值方法仅适用于中低频问题的求解。

综上所述，现有多孔介质板壳结构在模型建立中常对流体位移作简化假设，且解析法和数值解法均存在一定的局限性。本文从Biot理论和薄板理论出发，充分考虑多孔介质薄板固体骨架与内部流体间的相互作用，建立了一种求解多孔介质薄板声振问题的新模型，并结合高精度的齐次扩容精细积分法和精细元法[12]，提出一种在中高频段均具有较高计算精度的半解析、半数值求解方法。

1 多孔介质薄板控制方程的建立

图1为一多孔介质矩形薄板，薄板长、宽、厚分别为a，l，h；上下表面声压荷载分别为p1，p2；qi(i=x,y,z)为中面作用力。

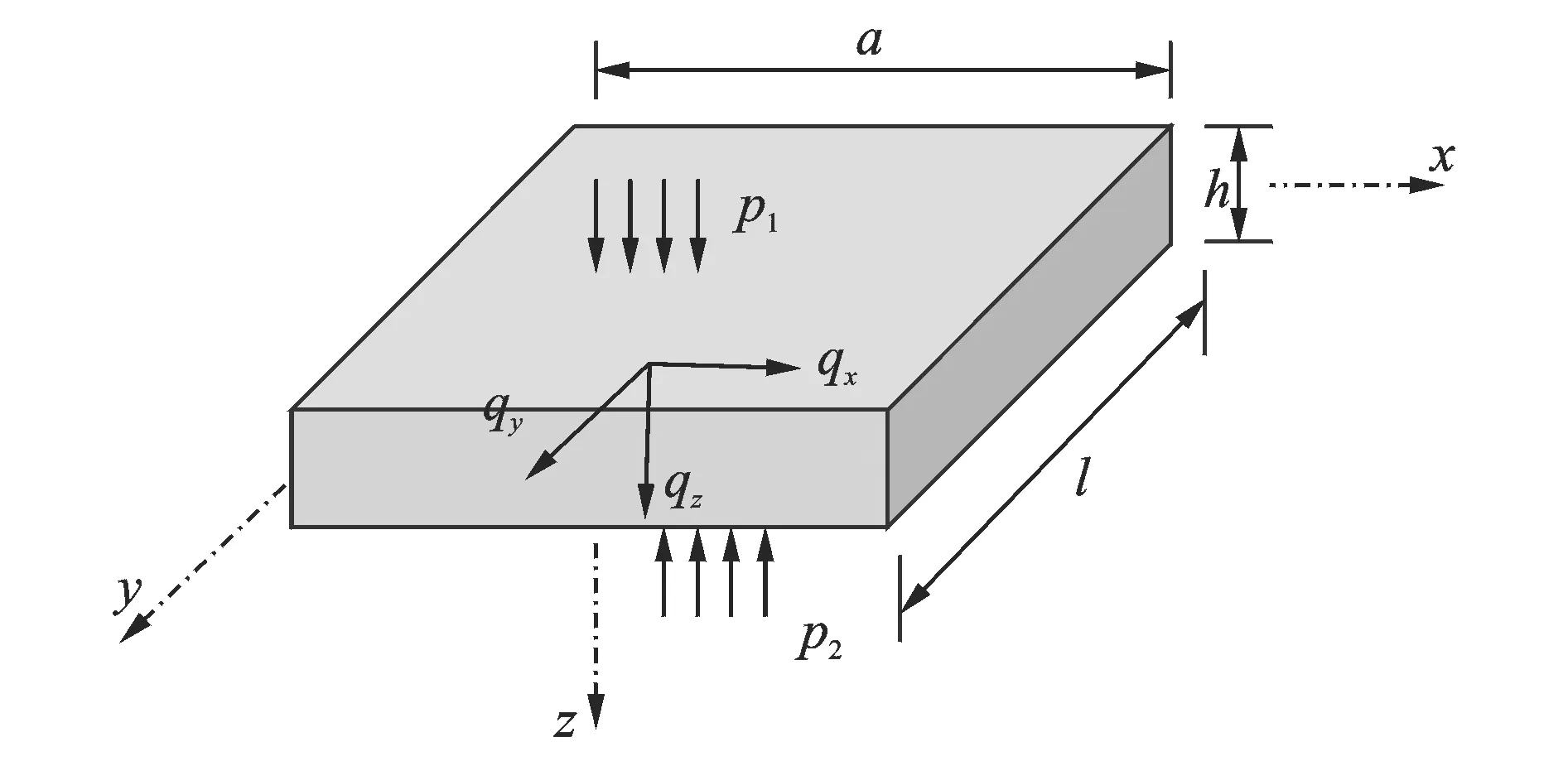
图1 多孔介质薄板示意图Fig.1 The schematic of thin rectangular porous plate

1.1 多孔介质薄板的本构关系

根据Biot三维理论，多孔介质材料的应力-应变关系如下[1]：

(1a)

(1b)

(1c)

式中e，ε分别为固体骨架和流体的体积应变；σi(i=x,y,z)为固体骨架沿三个坐标方向的正应力分量；τij,γij(i,j=x,y,z)分别为固体骨架上的三个切向应力和应变分量；Q表示微元体中固体骨架和流体体积应变之间的耦合系数；R表示维持一定数量的流体在微元体内所需的压力系数。p表示介质中的流体压力，φ为孔隙率；N，A类似于均匀各向同性弹性体中的拉美系数，N为剪切模量。式(1a)和(1b)为固体本构关系，式(1c)为流体本构关系。

由式(1c)中的第1式，可得

(2)

将之代入式(1a)得

(3)

根据薄板的直法线假设有：γxz=0，γyz=0，σz-φp=0，代入式(3)中的第3式可得

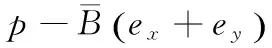
(4)

式中

1.2 多孔介质薄板固体骨架的内力-位移关系

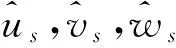
(6)

将式(6)代入固体骨架的应变-位移关系式，应变分量为

(7a)

内部流体的应变-位移关系

(7b)

将式(7a)代入本构关系式(5)，可得固体骨架的内力-位移关系

(8)

1.3 多孔介质薄板骨架的运动方程

对于多孔介质薄板骨架进行受力分析，可得运动方程如下[1]

(9)

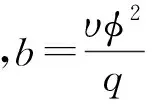
在谐激励外力作用下，运动方程(9)变为

(10)

1.4 多孔介质薄板内部流体的运动方程和本构方程

对于多孔介质薄板内部流体，根据Biot理论，其运动方程[1]为

(11)

式中ρ22=φρf+φρf(α∞-1)为流体介质的相对密度。

谐激励作用下，由式(11)可解出内部流体的位移幅值

(12)

结合固体骨架的位移模式式(6)，将式(12)沿薄板厚度方向积分，可得流体在中面任一点的位移幅值分量(平均值)

(13)

将式(12)的第3式代入流体z方向应变式(7b)的第3式，有

(14)

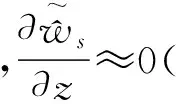
结合式(5)的第4式和式(7b)，频域内流体的本构关系简化为

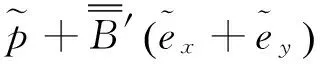
(15)

将式(12)代入式(15)，同时结合式(7a)和(13)，沿厚度方向积分可得

(16)

同理，将式(15)乘以z后，再沿厚度方向进行积分可得

(17)

式(16)和(17)为流体的运动控制方程。文献[5]中忽略了面内流体相对于固体的运动，假设除z坐标方向外其余两坐标方向的流体位移近似等于固体位移，即:us≅uf,vs≅vf,ws≠wf。不同于该文献，在式(16)和(17)的推导中，考虑了固体骨架和内部流体的相互作用，未对流体的位移引入任何假设，因而更加严谨精确，适用范围更广。

2 两对边简支多孔介质矩形薄板的一阶常微分矩阵控制方程

为了便于边界条件的计算，引入薄板的Kelvin-Kirchhoff等效剪力

(18)

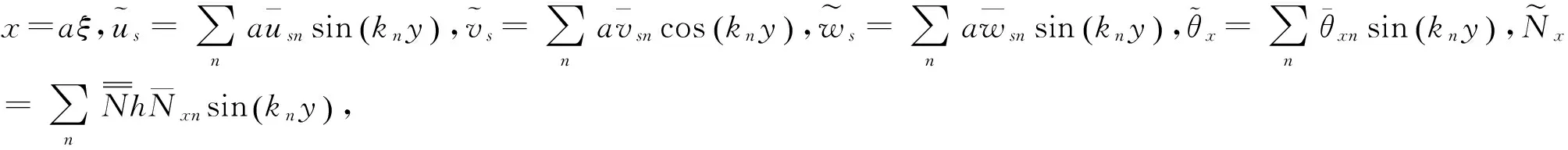
通过式(8)，(10)，(13)，(16)，(17)和(18)，经消去中间变量，可得12个状态向量的一阶常微分矩阵方程

(19)

3 一阶常微分矩阵控制方程的求解

利用高精度的齐次扩容精细积分方法和精细元法[12]，可以方便地求解上节推导的一阶常微分矩阵方程式(19)。

3.1 均布谐激励作用下控制方程的求解

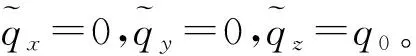
(20)

式中Zj，Zj-1分别为第j个单元前后两个节点处状态向量，Tj为单元传递矩阵，Qj是由外激励引起的转移项。式(20)移项后有

(21)

对于M个单元可得到M个形如式(21)的式子，写成矩阵形式如下

(22)

其中，未知状态向量个数为12(M+1)，方程个数为12M。一般情况下，薄板在x=0和x=a处各有6个给定的边界条件，将这些已知的边界条件代入到矩阵方程式(22)，即在矩阵方程中再增加12个方程，整理后方程数为12(M+1)，求解该方程组即可求出全部12(M+1)个状态向量。

3.2 集中谐激励作用下控制方程的求解

考虑一个两对边简支、另外两边任意支撑的多孔介质矩形薄板，在点(x=x0，y=y0)处有一个集中谐激励，其他外力均为零。在集中力作用点上增加一个受集中力作用的微小单元，如图2所示。

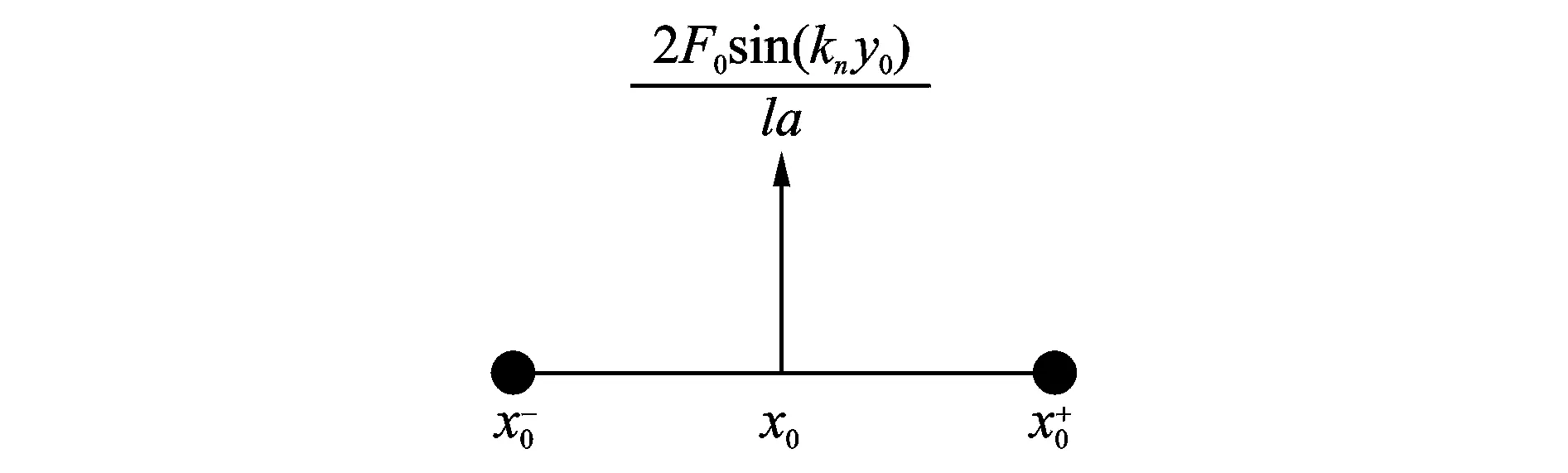
图2 集中激励单元示意图Fig.2 The unit under concentrated excitation

(23)

(24)

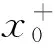
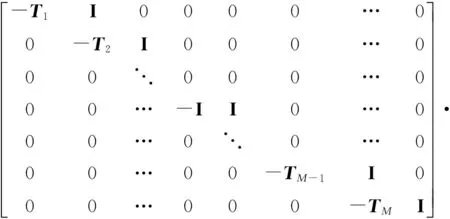
(25)

4 算例分析

从图3可以看出，本文模型与文献[4]模型无论在低频还是中高频段，两者的共振波峰频率以及共振频率处的峰值都吻合很好，说明了本文模型可行、有效。此外，与文献[3]和[4]比较，本文模型不仅能够计算四边简支边界条件，还可以灵活处理两对边简支、另两对边为任意边界条件的多孔介质薄板的振动问题(如图4所示)，适用范围更广，因此，本文模型具有较高的理论和应用价值。

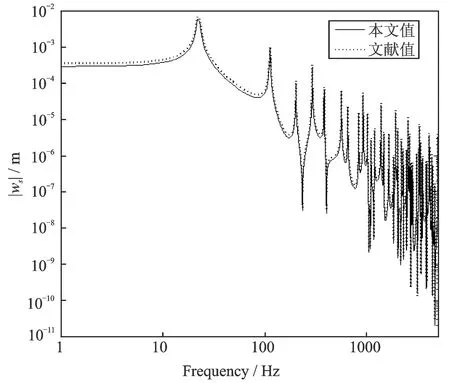
图3 四边简支多孔介质薄板的频率响应曲线Fig.3 Plate amplitude response versus frequency for a simply supported porous plate

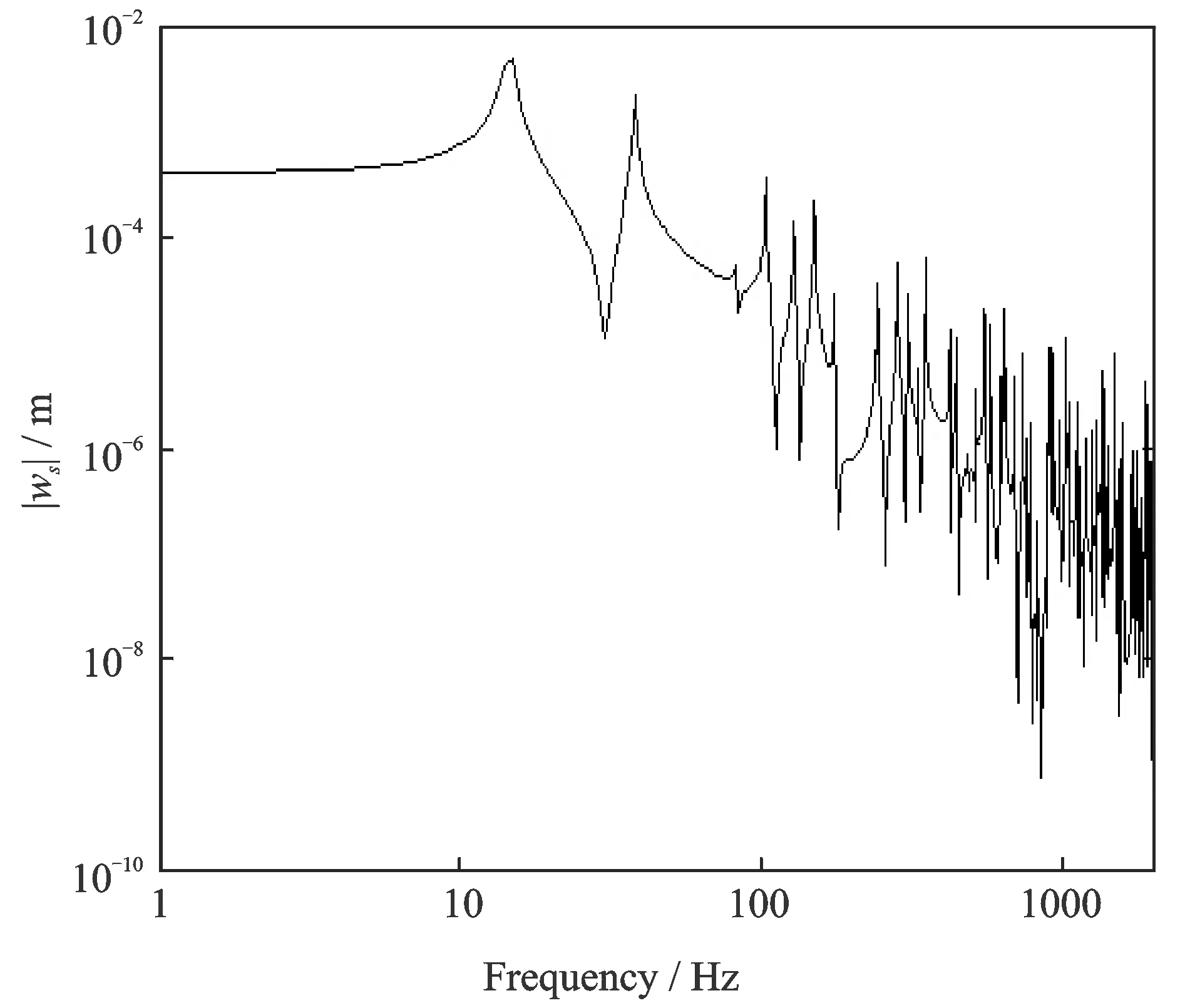
图4 两边简支、另两边一边固支一边自由多孔介质薄板的频率响应曲线Fig.4 Plate amplitude response versus frequency for a porous plate with two opposite edges simply supported and the other two edges clamped and free

算例2：考虑一个两对边简支矩形薄板[4]，尺寸为0.5m×0.5m×10.70mm，骨架密度ρs=1136kg/m3，流体密度ρf=1.213kg/m3，杨氏模量E=2.1×107Pa，泊松比μ=0.35，流体动黏度υ=1×10-3N·s/m2，扭转率α∞=1.2，达西渗透率q=2.7×10-10m2，孔隙率φ=0.69，其余参数处理同算例1。在板上表面x=0.15m，y=0.1m处施加幅值为1N的集中谐激励，观察板中点处的挠度。图5为四边简支情况下频率响应曲线与文献[4]的比较图；图6为两边简支、另两对边自由情况下的频率响应曲线图。

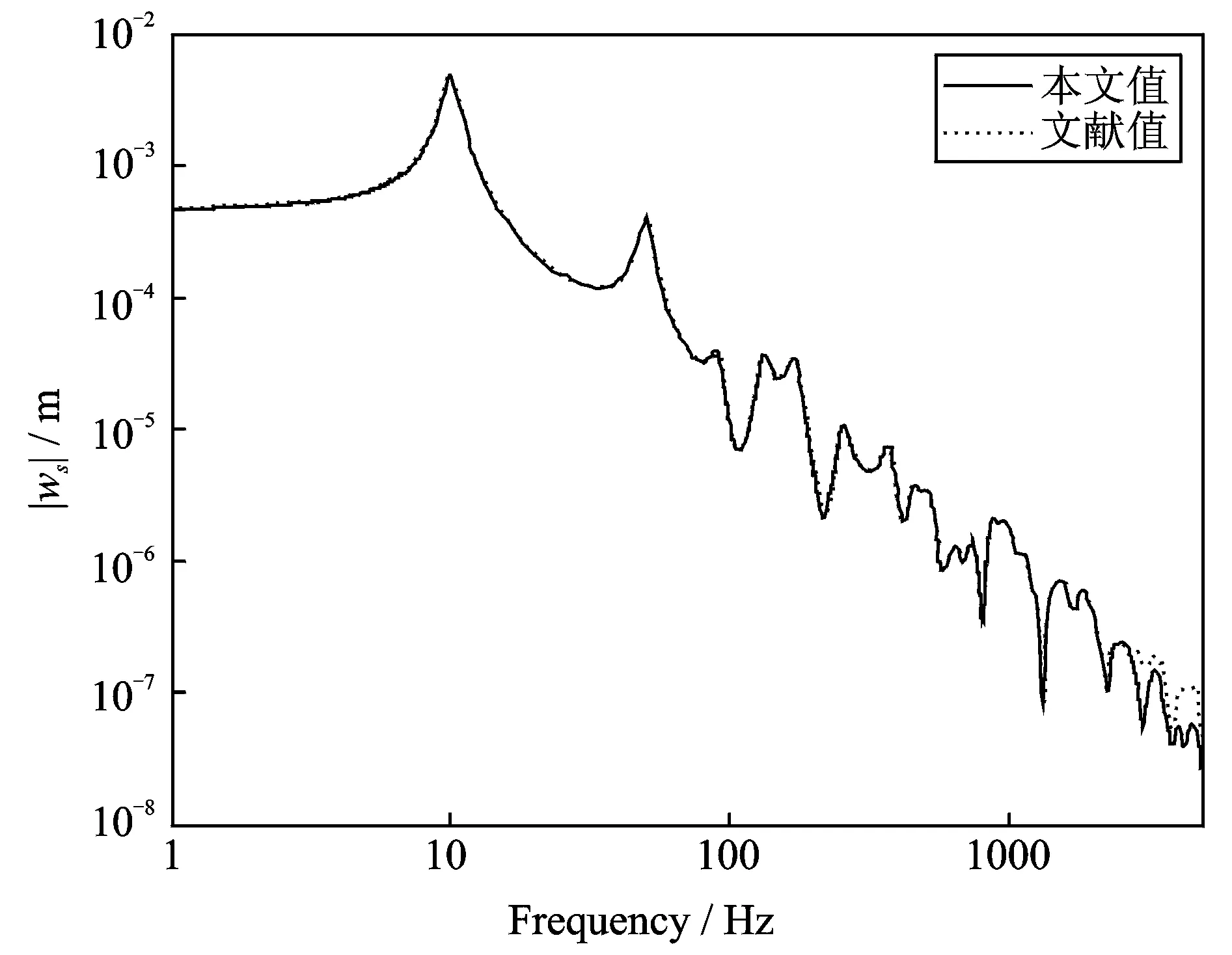
图5 四边简支多孔介质薄板的频率响应曲线Fig.5 Plate amplitude response versus frequency for a simply supported porous plate

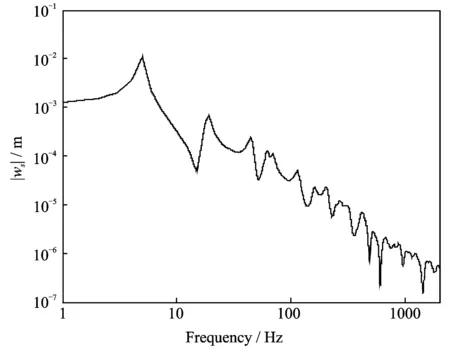
图6 两边简支、另两对边自由多孔介质薄板的频率响应曲线Fig.6 Plate amplitude response versus frequency for a porous plate with two opposite edges simply supported and the other two edges free

由图5可以看出，本文模型和文献[4]模型的位移频谱在低中频段完全重合，但在高频段2.5kHz之后，两种方法的位移幅值有较大差别。文献[4]模型的建立基于三个假设：1)板的厚度要远小于任何声波波长；2)板内流体z向位移幅值变化很小；3)忽略了流体相对于固体的面内位移。上述简化模型在低频阶段具有较高的精度，文献[5]中Leclaire等也用实验验证了该模型在低频段的有效性。但随着频率的增加，这种假设将很难满足，模型精度将会下降。文献[4]也指出了因对板厚有上述假设，其模型在高频段误差增大。本文模型充分考虑了三个方向上流体和固体的相对位移，且未对板厚进行任何假设，因此，从理论上讲相对于文献[4]中的简化模型，本文模型在中高频段内具有较高的精度。

5 结 论

本文从Biot理论和薄板理论出发，充分考虑多孔介质薄板骨架与流体的耦合作用，在对流体位移不做任何简化假设的前提下，首次推导出了多孔介质矩形薄板的一阶常微分矩阵方程。该模型的状态向量包含有内力分量、位移分量以及与声压有关的合力分量，可直接应用于各种边界条件，克服了现有文献中多孔介质薄板建模方法过于简化、边界条件处理困难等缺点，能很方便地求解两对边简支另两对边为任意边界条件下多孔介质薄板的声振问题。此外，在求解方法上，利用齐次扩容精细积分方法和精细元法，只要给定合适的精细积分步长和积分单元数，就能保证在中高频段的计算精度。因此，本文的多孔介质薄板精细积分模型推导严谨，精度高，适用范围广，该模型还可为研究其他边界条件下多孔介质矩形薄板声振特性问题提供理论基础。

[1] Boit M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅰ. Low-frequency range[J]. J. Acoust. Soc. Am., 1956,28(2):168—178.

[2] 刘志军,夏唐代,黄睿,等.Biot理论与修正的Biot理论比较及讨论[J].振动与冲击,2015,34(4):148—152.

Liu Z J, Xia T D, Huang R, et al. Compare and discussion for Biot theory and modified Biot one[J]. Journal of Vibration and Shock. 2015,34(4):148—152.

[3] Theodorakooulos D D, Beskos D E. Flexural vibrations of poroelastic plates[J]. Acta Mechanica, 1994,103:191—203.

[4] Leclaire P, Horoshenkov K V. Transverse vibrations of a thin rectangular porous plate saturated by a fluid[J]. Journal of Sound and Vibration, 2001,247(1):1—18.

[5] Leclaire P, Horoshenkov K V, Swift M J, et al. The vibrational response of a clamped rectangular porous plate[J]. Journal of Sound and Vibration, 2001,247(1):19—31.

[6] 陈卫松,邱小军.多孔弹性介质三层夹心板的隔声性能研究[J].应用声学,2008,27(2):118—124.

Chen W S, Qiu X J, Sound insulation character of three-layer panels one with elastic porous materials[J]. Applied Acoustics, 2008,27(2):118—124.

[7] 宁景锋,赵桂平,穆林，等.含有空气背衬层的分层多孔材料的吸声性能研究[J].振动工程学报,2014,27(5):734—740.

Ning J F, Zhao G P, Mu L, et al. Study on sound absorption properties of multilayer porous material structure backed with air gap[J]. Journal of Vibration Engineering, 2014,27(5):734—740.

[8] Atalla N, Panneton R, Debergue P. A mixed displacement-pressure formulation for poroelastic materials[J]. Journal of the Acoustical Society of America,1998,104(3):1444—1452.

[9] Kang Y J, Bolton J S. Finite element modeling of isotropic elastic porous materials coupled with acoustical finite elements[J]. J. Acoust. Soc. Am., 1995,98(1):635—643.

[10]Batifol C, Zielinski T G, Ichchou M N, et al. A finite-element study of a piezoelectric/poroelastic sound package concept[J]. Smart Materials & Structures, 2007,16(1):168—177.

[11]胡莹,陈克安,M A Galland,等.基于(U,P)方程含多孔材料有源声学结构的声学性能研究[J].声学学报,2011,36(3):271—280.

Hu Ying, Chen Ke′an, M A Galland, et al. Sound transmission of double-wall active sound package with porous materials based on (U,P) formulation[J]. Acta Mechanica, 2011,36(3):271—280.

[12]Ni Q, Xiang Y, Huang Y Y, et al. Modeling and dynamics analysis of shells of revolution by partially active constrained layer damping treatment[J]. Acta Mechanica Solida Sinica, 2013,26(5):468—479.

[13]曹志远.板壳振动理论[M].北京:中国铁道出版社,1989.

Cao Zhiyuan. Vibration Theory of Plates and Shells[M]. Beijing: China Railway Press, 1989.

附录 系数矩阵A，B和非齐次向量F中的非零元素

1.系数矩阵A中的非零元素

2.系数矩阵B中的非零元素

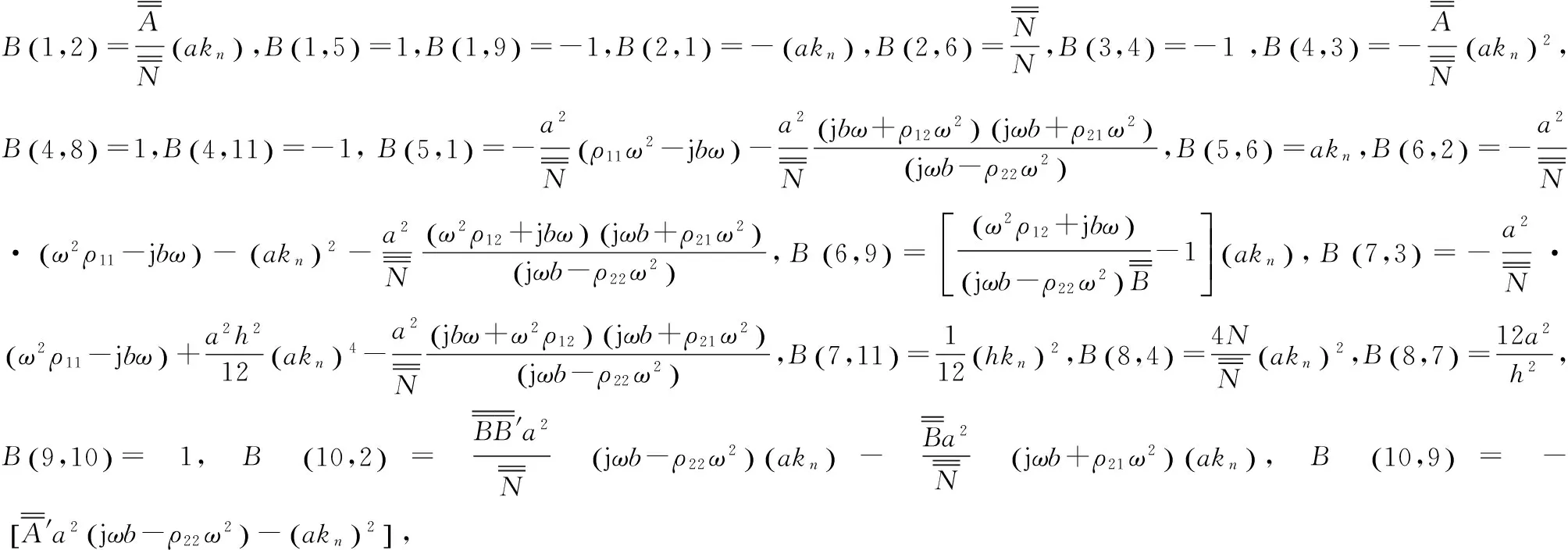
3.非齐次向量F中的非零元素

A precise integration model of a thin rectangular porous plate

XIANGYu1,2,JIANGHong-hua1,2,YUANLi-yun1,2,LUJing1,2

(1.Automotive & Transportation Engineering Institute, Guangxi University of Science and Technology,
Liuzhou 545006, China; 2.Guangxi Key Laboratory of Automobile Components and
Vehicle Technology, Guangxi University of Science and Technology, Liuzhou 545006, China)

Based on the three dimensional Biot theory and the elastic theory of thin plate, the first order differential equations of a thin rectangular porous plate under harmonic excitation were established by considering the coupling effect between the solid phase and the fluid phase. Employing the extended homogeneous capacity precision integration method, transverse vibrations problem of a thin rectangular porous plate was discussed with simply supported boundary condition in two opposite edges. In the numerical examples, both the uniform force and unit point force were taken into account. Comparisons with the classic example have verified the feasibility and effectiveness of the present model. The present model was high precision, which was derived rigorously and easy to conduct various boundary conditions. It can be applied in higher frequency range than the numerical method.

thin rectangular porous plate; absorption; Biot theory; extended homogeneous capacity high precision integration method

2015-08-05；

2016-04-25

国家自然科学基金资助项目(11162001,11502056);广西自然科学基金资助项目(2015GXNSFBA139007)

TH34; O422.8

：A

1004-4523(2016)06-1020-08

10.16385/j.cnki.issn.1004-4523.2016.06.010

向宇(1963—)，男，教授。电话：(0772)2695662； E-mail：gxutxy@126.com