揭秘量子密码、量子纠缠与量子隐形传态
施郁
复旦大学物理学系,上海 200433
揭秘量子密码、量子纠缠与量子隐形传态
施郁†
复旦大学物理学系,上海 200433
以光子的偏振态为例,对量子力学、量子态、量子密码、量子纠缠和量子隐形传态作简要通俗而又力求准确的介绍。首先通过与经典物理的对比,引进量子力学的基本思想和量子态的基本涵义;接着介绍量子密码的BB84量子密钥分配方案;然后介绍量子纠缠,强调它不违反相对论。在此基础上,介绍了量子隐形传态,强调了经典通信在这个过程中的必不可少。
量子力学;量子态;量子密码;量子纠缠;量子隐形传态
量子信息指利用量子力学的基本原理进行信息处理,在最近一些年得到了很大发展。量子信息包括量子通信、量子计算等等。量子通信包括量子密码、量子隐形传态等等。量子隐形传态和量子计算都基于量子纠缠。量子纠缠是量子力学中的一个基本概念。
1 揭秘量子力学与量子态
为了解释什么是量子力学,我们从经典物理说起。
经典物理包括以牛顿三大定律为核心的牛顿力学(或称经典力学)以及以麦克斯韦方程组为核心的经典电动力学(或称电磁学)。对于速度接近光速以及强引力场情况,还要考虑狭义及广义相对论,但是相对于量子力学而言,它们仍然属于经典物理的范畴。
在经典物理中,每个物理量,比如位置、动量、角动量、电场强度、电流等等,在每个时刻都有明确的取值,都是一个客观实在。它们随时间变化的情况就是动力学,由牛顿力学及经典电动力学的基本定律决定。只要知道某个时刻的物理量的值,就可以从动力学得到其他任意时刻的取值。因此本质上经典物理是决定论的。
经典物理里也有几率,或称概率,但这是一种粗粒化描述。在不了解或者无法控制细节时,考虑各种可能性,从而得到几率分布。比如掷骰子。骰子的运动其实是一个决定论的过程,没有本质上的随机性。如果了解它的力学细节,比如质量分布、初始位置、方位、速度、整个下落过程中的受力情况等等,其实是可以预言最后哪一面朝上的。当然,在实际中一般做不到这一点。对于各种细节情况作平均,就可以预言,如果投掷N次,其中每一面朝上的次数大约N/6次。也就是说,每一面朝上的几率大概是1/6。
经常有这样的情况,即细节描述不但不可能,而且没有必要,而几率描述更抓住问题的本质。比如一团气体在给定温度下,各种微观状态有一个几率分布,由此可以得到给定温度下的宏观性质,比如平均总能量、压强等等。这就是统计物理。基于经典力学的经典统计物理中的几率抓住了问题的本质,但这种几率和骰子类似,不是实质性的,也就是说,微观细节仍然是服从经典物理的决定论过程。
那么,什么样的几率是实质性的,也就是说背后没有决定论的过程?答案就是量子力学中的几率。量子力学的中心概念是量子态,而根据量子态,可以计算出各种几率分布。下面我们将了解到,量子态比几率分布的涵义还要多。
量子态不是一个物理量,而是一个描述。由此决定各相关物理量被测量后的各种取值的几率,从而可以计算出每个相关物理量的期望值,或称平均值。一旦做了某个物理量的测量,就得到这些可能值中的一个,量子态也相应地更新为一个新的量子态。在这个量子态上,刚测得的物理量取值的几率为1。
举一个例子。光有个性质叫偏振,代表了电场振动方向,它总是位于与传播方向垂直的平面上。如果偏振方向沿着这个平面上的一个特定方向,这种光就是线偏振光。如果偏振方向在这个平面上旋转,这种光就是圆偏振光。偏振性质不同的光可以混合成非偏振或者部分偏振光,而非偏振的自然光透过偏振片,可以产生偏振方向沿着透光轴的线偏振光。如果让线偏振光垂直入射一个偏振片,它透过的强度是原来强度的cos2θ,其中θ是光入射前的线偏振方向与偏振片透光轴方向的夹角。
光是由光子组成的,光子服从量子力学。现在让我们考虑单个的光子。单个光子的偏振方向总是位于与动量正交的平面上。线偏振的光子透过偏振片的几率是cos2θ。
几率的涵义如下:如果有N个(N很大)偏振量子态都是|θ〉的光子分别入射到这个偏振片上,也就是说,对于同样的量子态|θ〉,重复N次相同的过程,那么有Ncos2θ个光子透射过去。
但是对于每一个光子来说,无法预测它究竟能否透射过去,完全不能。所以我说量子力学的几率是实质性的。
量子力学有一套理论框架描述这些性质。光子的偏振由一个量子态描述,我们可以把它记为|ψ〉,它在数学上是一种矢量。
我们知道,空间中的矢量,比如位置,由几个坐标(或者叫分量)确定。任意一个矢量都可以分解为几个互相正交的基本矢量。它们平行或反平行于坐标轴,长度大小就是坐标的绝对值,方向由坐标的符号代表,它们称作基矢。与之类似,量子态这种矢量也可以分解为几个互相正交的基矢,它们称为基矢态。这里的矢量不是在我们所生活的空间,而是在一个抽象的数学空间里,称作矢量空间。它是这个量子系统的所有可能的量子态的集合,服从一定的运算规则。这些矢量的正交也有它的定义。
在我们生活的空间里,坐标的选择是任意的。与之类似,对于一个量子态来说,选择哪一套基矢态来展开或者分解也是任意的。但是为了计算某个测量的几率,选择与这个测量对应的基矢态比较方便。光子透过偏振片可以看作一个测量过程:如果偏振方向沿着偏振片的透光轴方向,就会穿透;而如果垂直于透光轴方向,就不能穿透。
为简单起见,我们考虑某个垂直入射偏振片的线偏振光子。假设在偏振片上定义一个xy平面,光子的线偏振沿着θ方向。我们将这个偏振量子态记作|θ〉。
现在先假设偏振片的透光轴沿着x方向。为了计算光子透过偏振片的几率,可以把光子原来的量子态分解如下:
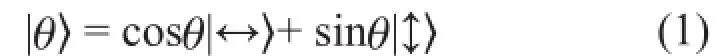
其中|↔〉与|↕〉互相正交,|↔〉代表光子偏振方向沿着x方向,即目前偏振片的透光轴,|↕〉代表光子偏振方向沿着y方向,即垂直于偏振片的透光轴。
光子入射偏振片,量子态变得非此基矢态即彼基矢态:要么变成|↔〉,从而透过偏振片;要么变成|↕〉,从而不能通过偏振片。前者的几率是cos2θ,后者的几率是sin2θ。几率等于展开式(1)式右侧各基矢态前面系数(通常称作展开系数)的模的平方。这是由量子态决定几率的基本规则。这些系数的模的平方之和等于1,因为各种可能的几率之和应该是1。因此,光子穿透偏振片的几率是cos2θ,穿透后的量子态变为|↔〉。
现在我们改变一下偏振片的方位,将它逆时针转动45°,然后再将处于同样偏振量子态|θ〉的光子入射。现在将光子的量子态|θ〉作如下分解比较方便:
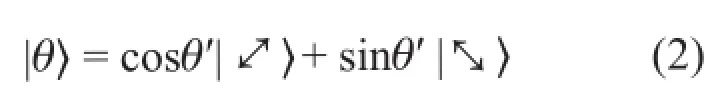
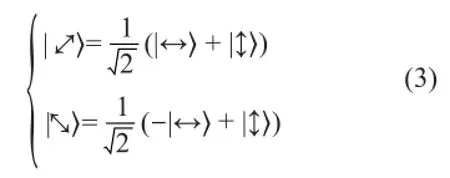
反过来就是
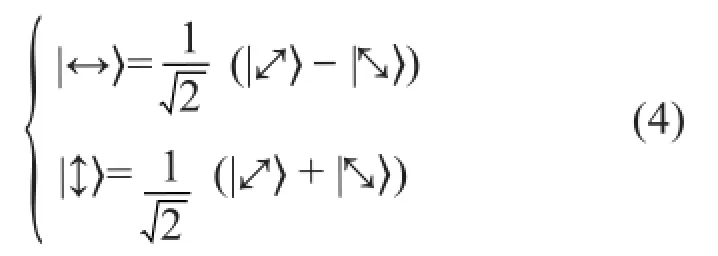
后两式也可以分别通过将θ= 45°和θ=135 °代入式(2)得到。
也有复杂一点的测量方法,可以做到测量一个光子的偏振态而且不失去它。比如,借助于一个双折射晶体和两个偏振片,使得每个光子都能随机地从一个偏振片透射出来,非此即彼,每个偏振片分别对应于一个基矢态。下面所讨论的对偏振态的测量就是这样。为了简单起见,这里不赘述细节。
一般来说,一个量子态用基矢态展开,比如圆偏振态用线偏振基矢态展开,展开系数是复数。但是为简单起见,本文所用的例子中,展开系数都是实数。
对于不同的物理性质有不同的量子态。比如偏振是一个物理性质,动量是另一个物理性质。如果不同的物理性质之间没有耦合,相应的量子态也没有耦合,只需要考察相关的量子态。比如在上面这个例子里,关于光子的动量或者位置当然也有量子态,但是与我们关心的偏振现象没有关系,所以不去关心。
在测量之前,量子态随时间的演化是由一个动力学方程决定的,这个方程被称作薛定谔(E. Schrödinger)方程,因为历史上第一个例子(描写氢原子中的电子)是由薛定谔提出的。与相关物理性质有关的能量是一个常数时,相应的量子态在测量之前就不变。下面的讨论都属于这种情况。在量子力学里,量子态、几率分布以及物理量的期望值都可以有决定论的动力学演化,但是这改变不了量子力学的几率本质,因为在每个量子态上,作一个物理量的测量,都有一个内在随机性。
什么情况下用经典物理,什么情况下必须用量子力学?它们的分界线在哪里?严格来说,这是一个没有完全解决的问题。对于具体的实际情况(for all practical purposes),一般能够判断。比如,一般来说,小分子层次以下的微观粒子必须要用量子力学,而我们周围的宏观物体服从经典物理。但是随着实验技术的进步,越来越大的物体表现出量子效应。所以有可能所有的物质本质上都服从量子力学,只是在环境的作用下,表观上显示出经典物理。但是也有可能量子力学的适用范围是有限的。笔者认为,按物理学目前的水平来说,这两种可能都是存在的。
2 量子密码,巧妙在哪?
一个量子系统的基矢态的数目可能无限多,基矢态对应的物理量取值的分布是连续的。比如动量量子态,不同的动量就对应不同的基矢态,而动量是可以连续变化的。一个量子系统的基矢态数目也可能是有限的,基矢态所对应的物理量取值的分布是分立的,比如我们这里讨论的偏振量子态。分立的情况适合用于信息处理,这就是量子信息。可以用一个双态系统(基矢态只有两个)的两个基矢态代表比特(二进制数)0和1。因为它们是量子态,所以它们代表的是量子比特,服从量子力学的规律。
量子信息包括若干方面。本章介绍量子密码。密码的一个关键是密钥,比如一串比特,即每个数是二进制数0或1。发出信息的一方将信息转换为一串比特,然后将每个比特与密钥中的比特以二进制规则相加,而且每个比特保持一位,即逢2回到0。这就是加密。加密后的比特串发给接收信息的一方。其收到后再将每个比特分别与密钥中的比特相加并逢2回0(也就是相减,二者结果一样),由此就得到原来的信息。这就是解密。量子密码的一个主要方法就是利用量子态产生密钥,这就是量子密钥分配。注意,最后得到的密钥本身仍然是经典的。
量子密钥分配的一个主要方案是由Bennett和Brassard在1984年提出的BB84方案[1]。下面我用光子的偏振态解释。假设两个人A和B要确定一组共享的密钥。A先随机地用|↔〉或者|↔〉代表0,并随机地用|↕〉或者|↔〉代表1。A以此方法产生一批光子,发送给B。B对于每个光子测量其偏振态,每次测量又都是随机选择|↔〉和|↕〉这组基或者|↔〉和|↔〉这组基。然后A和B交流,对于每个光子的产生和测量,分别是用了哪组基,但不说明具体的态。他们的这个交流不需要保密,可以是公开的。然后将产生和测量用的基不一样的情况剔除,剩下的光子的偏振态在A发出和B测量后应该是一样的,而且别人不知道。
理想情况下,这些光子既然产生与测量的基一致,那么它们在B测量后的偏振态也就应该与在A处产生时一样,除非被“窃听”过。假设某个光子曾在传输途中被E截留,E测量其偏振态,然后再发给B。这就是所谓“窃听”。E当时不知道该光子是通过哪组基产生的。假设他随机地选择这两组基之一来测量。如果E测量所用的基碰巧与光子在A处产生时的基一致(有1/2几率是这样),那么E就会正确地测量得到光子的偏振态,而且未作改变,又发给了B。这样,光子的偏振态就与没有被窃听的情况一样。B收到该光子后,如果用与A一样的基测量,得到的结果就与光子产生发出时的偏振态一样。E的窃听就不能被发现。但是如果E窃听时用的基与原来的不一样(有1/2几率是这样),那么测量之后,光子偏振态就改变了,变成E测量所用的基上的两个基矢态之一。B 收到该光子后,如果用与A一样的基测量,那么其中只有1/2几率得到的结果与产生时一样。另有1/2几率得到的结果与产生时的偏振态相正交,这就出错了。这些几率是从式(3)和(4)算出的。因此总的来说,如果存在窃听,就会引起可观的错误率,在上述窃听方案下,引起的错误率是1/4。
举个更具体的例子。假设A产生一个偏振态|↔〉的光子,被E截获,E在|↔〉和|↕〉这组基上测量,结果当然是|↔〉。然后E将光子发出,被B收到。B选择了在|↔〉和|↕〉这组基上测量(所以后来这个光子的信息在A和B交流产生与测量时所用的基以后才会留下),结果当然还是|↔〉,情况与没有被E窃听的情况一样。但是如果E截留后,在|↔〉 和|↔〉这组基上测量,结果要么是|↔〉 ,要么是|↔〉。测量后,发给B。B在|↔〉和|↕〉这组基上测量。不管光子偏振态在E测量后是|↔〉,还是|↔〉,B的测量结果中有1/2几率是|↔〉,1/2几率是|↕〉。总之,虽然B测量该光子所用的基与A产生它时一致,但是有1/2几率光子的偏振态与产生时不一样了。
因此A和B可以从产生与测量所用的基相同的光子中选择一部分来做抽查,将它们产生与测量的偏振态作比较。如果没有被窃听过,这些光子被B测量得到的结果应该与在A处产生时一样;而如果被窃听过,其中有一些光子的偏振态就有变化。如果E每次窃听是完全随机选择这两套基中的一个,那么偏振态发生变化的光子占1/4。由此A和B可以判断出是不是存在窃听。
这个方案的保密性基于不同的基之间的不相容,既互为叠加态。
3 量子纠缠违反相对论吗?
现在我们开始讨论量子纠缠。这是复合量子系统(由2个或以上的子系统构成)的量子态的性质。
我们还是用偏振态作为例子。考虑两个光子a和b的偏振量子态, 记作|ψ〉ab。下标代表这个态的载体。有一种可能是这两个光子a和b的偏振分别由一个量子态描述,也就是说,两者是互相独立的。这可以写成
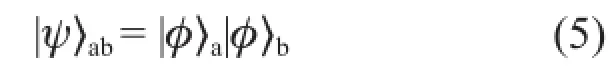
这种情况下,对a光子做任何测量或操作都不会影响b光子的量子态,二者相互独立。无论你将|φ〉a或者|φ〉b用什么样的一套基矢态分解,都改变不了|ψ〉ab=|φ〉a|φ〉b,这样的量子态称作可分离态。
但是还有一种情况,每个光子的偏振没有独立的量子态,也就是说|ψ〉ab不可能写成|φ〉a|φ〉b的形式。对于光子a的偏振,或者光子b的偏振,不管选择怎样的一套基矢态,|ψ〉ab的展开式中总是至少有两项相加。这样的量子态称作量子纠缠态。比如:
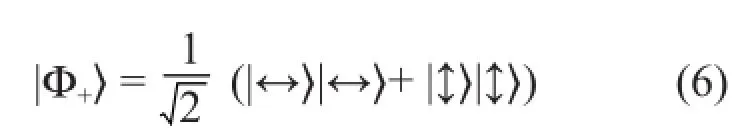
这里左边是两个光子组成的复合系统的态,右边每一项中的两个态依次分别是两个光子a和b的基矢态。每个态的载体省略未写,一方面是为了简洁,另一方面也为了后面将这个表达式用于另外的光子。如果这两个光子都用|↔〉和|↔〉这组基,那么|Φ+〉 就改写为另一种形式。将变换式(4)代入式(6),得到
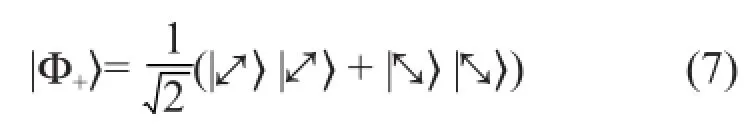
式(6)和(7)代表的是同一个双光子态|Φ+〉。
为了讨论方便,我们假设光子a被A所控制,光子b被B所控制。现在A测量a的偏振,假设偏振片的透光轴沿着x方向,那么根据式(6),可以知道有1/2的几率测得它的偏振沿着x,测量之后其量子态变为|↔〉。式(6)的两项之和变为第一项,也就是说整个系统的态变为|↔〉|↔〉。在这个态中,光子b的态显然是|↔〉。另一方面,如果a的偏振测得是沿y方向,也就是说它的量子态在测量之后变为|↕〉。式(6)中的两项之和变为第二项,也就是说整个系统的态变为|↕〉|↕〉,在这个态中b的态是|↕〉。因此,A通过对两个纠缠光子中一员a的偏振进行测量,可以预言另一个光子b的偏振。
这一点奇怪吗?其实经典几率中也有类似的情况。量子态是一种描述,经典几率也是一种描述。假设有一个容器里装着红色的球,另一个容器里装着蓝色的球,但是从外面看不出哪个容器装着什么颜色的球。现在随机选择一个容器,从中拿出两个球分别放在密封的盒子里,交给A和B。A和B只知道它们来自同一个容器,所以颜色一样,但不知道颜色究竟是什么。然后A和B 分别到相距很远的两地。在A打开盒子之前,她的球是红色和蓝色的几率各为1/2。A打开盒子,知道了她的球的颜色,所以也立即知道了B的球的颜色。对此,没有人觉得奇怪。所以在这一点上,量子纠缠还不奇怪。
与之相比较,量子纠缠的不同或者说“奇怪”如下。这个不同来自量子态具有超越几率的涵义,而测量可以选择不同的基。A完全可以用另外一个基来测量光子a的偏振态。比如可以用|↔〉和|↔〉这组基。那么将|Φ+〉写成式(7) 比较方便。从中可以看出,A有1/2的几率测得光子a的偏振沿着45°方向,也就是说,测量之后a的量子态变为|↔〉。式(7)的两项之和变为第一项,也就是说整个系统的态变为|↔〉 |↔〉。其中光子b的态是|↔〉。另一方面,如果光子a的偏振测得是沿135°方向,也就是说它的量子态在测量之后变为|↔〉。式(7)中的两项之和变为第二项,也就是说整个系统的态变为|↔〉|↔〉,其中光子b的态是|↔〉。
但是,这并不意味着违反相对论。虽然A通过对光子a的测量,确定或者说预言了光子b的偏振,但是如果A不把测量结果告知B,B是无法确认的。如果这时B测量光子b,结果确实与A的预言一致。但是,原来的纠缠态也预言了B是有1/2几率测量得到b的这个偏振态的,所以B无法觉察A做过测量。如果A分别对处于同样的|Φ+〉的N个光子对a和b作测量,N个光子a的测量结果是随机分布的,由此导致的A对光子b的态的预言也是随机分布的。对于光子b来说,两种情况——一个是在纠缠态|Φ+〉下测量,一个是在光子a已经被A测量但是B不知道——多次测量的几率分布和相关物理量的平均值,结果是完全一样的。也就是说单靠B对于光子b的测量,是无法分辨的,而如果A将测量光子a所得的结果告诉B,这个通信过程就受到物理定律的限制,不能超过光速。对这一点的忽略使得很多人觉得量子纠缠很神秘。
我们再列举3个纠缠态的例子:
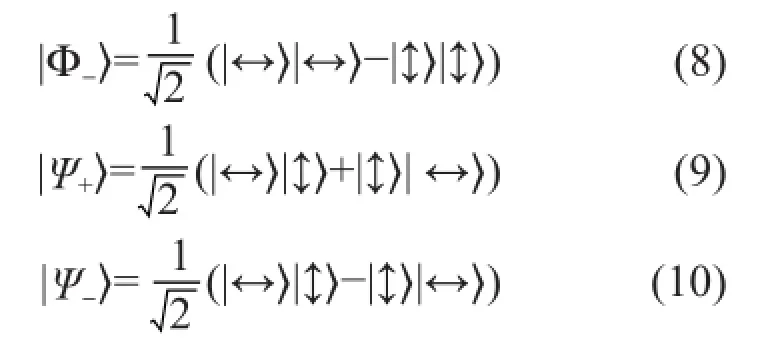
|Φ+〉、|Φ-〉、|Ψ+〉和|Ψ-〉这4个纠缠态的结构类似,有时统称贝尔(Bell) 态, 其中|Ψ-〉又称爱因斯坦-波多尔斯基-罗森-玻姆(EPRB)态。它们都是最大纠缠态。上面与|Φ+〉相比较的经典情形也适用于与|Φ-〉作比较,而可以用来与|Ψ+〉和|Ψ-〉相比较的一个经典情形是一双手套(一左一右)分装在一个密封盒子里,被A和B随机拿走其中一只。A打开盒子知道自己的是哪一只之后,立即知道B处的手套是哪一只。量子纠缠超越这一点,因为可以在另一个基上测量。
贝尔态也可以作为两光子偏振态的基矢态。将贝尔态的表达式(6)、(8)~(10)反过来,可以得到
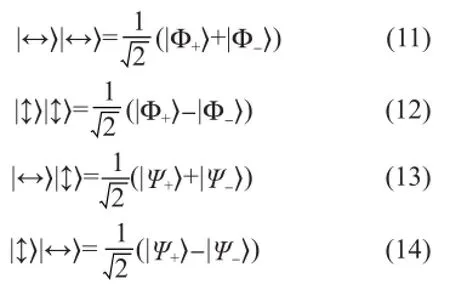
量子纠缠的特别之处是爱因斯坦、波多尔斯基和罗森首先发现的[2],然后薛定谔赋予“量子纠缠”这个名词,并指出“我不说这是量子力学的一个特征,而说这就是量子力学的特征,它导致了与经典思想的彻底偏离”[3]。关于爱因斯坦等人的观点以及后来的发展,笔者将另文评述。
4 量子隐形传态
前文已指出,虽然纠缠的两个粒子中的一个被测量造成整个量子态发生变化,但是除非将测量结果通知另一方,这个变化不会被另一方所觉察。所以量子纠缠与相对论没有矛盾,和平共处。
另一方面,如果借助经典通信,就可以利用量子纠缠实现一些特殊的信息处理过程。量子隐形传态[4]就是其中的典型。下面我们还是用光子偏振态来介绍。
在量子隐形传态中,除了一对处于最大纠缠态(比如|Φ+〉)的光子a和b以外,还有一个单光子c,这个单光子c的偏振量子态|ψ〉可以是未知的。上面我们说过任意的量子态都可以用基矢态展开,所以|ψ〉总可以写成
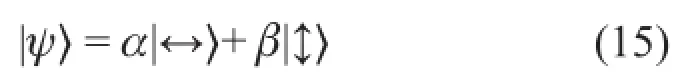
其中α和β是展开系数,可以是未知的。处于纠缠态|Φ+〉中的光子a和b分别为A和B控制,A和B处于可以相距很远的两地,光子c也处于A处。隐形传态是将光子c的量子态传到光子b上,使得b的量子态变为|ψ〉,不再与光子a纠缠,而光子c和a则纠缠起来。过程如下:
一开始,3个光子的量子态是
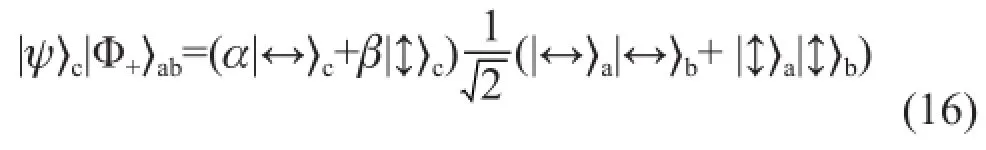
将右边展开,也就是
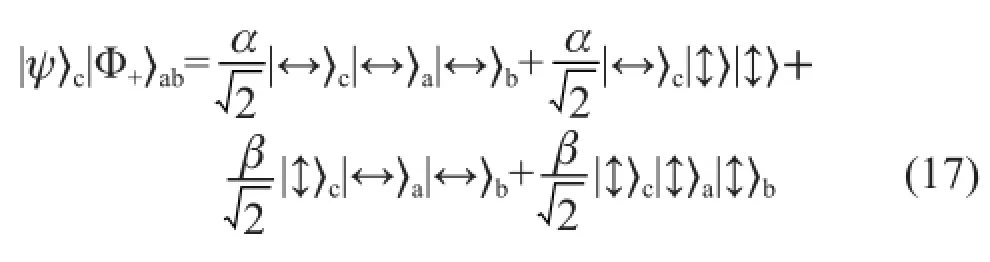
为了方便起见,现在我们对于c和a这两个光子用上一章最后所说的贝尔态作为基矢态展开。将式(11)~(14)代入,可以发现这3个光子的偏振态可以写为
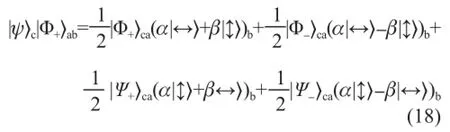
注意,到目前为止,物理上什么也没做,只是数学表达式的改写。
现在A对于她所掌握的c和a两个光子作一个贝尔测量,也就是一个以4个贝尔态为基矢态的测量,从而c和a的量子态以各1/4的几率成为4个贝尔态中的一个,相应地,这3个光子的量子态成为上式4项中的一项。
这是前面所讲的2个纠缠光子中一方被测量的情况的推广。如果A不把测量结果通知B,B无法觉察b的任何变化。隐形传态的一个关键步骤是A告知B关于光子c和a的测量结果,即光子c和a的量子态变成了哪个贝尔态。这可以用通常的经典通信手段。B从而就知道了光子b处于以下4个可能量子态中的哪一个:
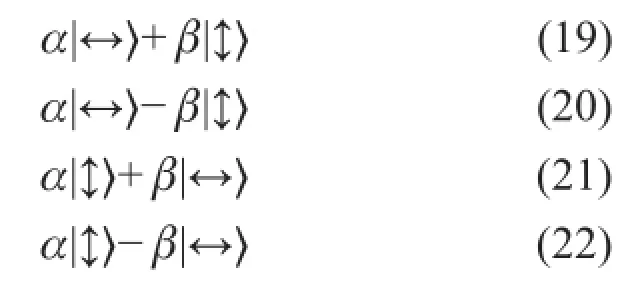
注意,α和β可以是未知的。但是不管α和β是什么, 这4个态与最初c的态|ψ〉=α|↔〉+β|↕〉的关系是普适的,即不依赖于α和β。上列4个可能的态中,从上到下,第一个态就是|ψ〉,第二个态是将基矢态|↕〉变为−|↕〉,第三个态是将|↔〉与|↕〉互换,第四个态是将基矢态|↔〉变为|↕〉,同时又将|↕〉变为−|↔〉(注意,这两个改变是同一操作对于不同基矢态的效果)。
所以得知A的测量结果后,B只要对b作相应的操作,总可以得到|ψ〉。具体来说,如果c和a的态成为|Φ+〉,b的态就是|ψ〉,不需要做任何操作;如果c和a的态成为|Φ-〉,那么对b做使得|↕〉变为−|↕〉的操作;如果c和a的态成为|Ψ+〉,那么对光子b做将|↔〉与|↕〉互换的操作;如果c和a的态成为|Ψ-〉,那么对b做将|↔〉变为−|↕〉,同时又将|↕〉变为|↔〉的操作。这些操作可以通过光子b的动力学演化实现。
这样,就将量子态|ψ〉从光子c传到了光子b上。注意:①光子本身没有传送,是量子态被传送;②该量子态原来的载体光子c改载其他态,事实上它与光子a一起处于一个纠缠态;③经典通信必不可少。最后一点容易被人忽略而造成误解。
(2016年5月23日收稿)■
[1] BENNETT C H, BRASSARD G. Quantum cryptography: public key distribution and coin tossing[C]//Proceeding of IEEE International Conference on Computers, Systems and Sigmal Processing, IEEE, New York, 1984.
[2] EINSTEIN A, PODOLSKY B, ROSEN N. Can quantum-mechanical description of physical reality be considered complete? [J]. Phys Rev, 1935, 47: 777-780.
[3] SCHRÖDINGER E. Die gegenwärtige situation in der quantenmechanik [J]. Naturwissenschaften, 1935, 23: 807-812; 823-828; 844-849.
[4] BENNETT C H, BRASSARD G, CRÉPEAU C, et al. Teleporting an unknown quantum state via dual classical EPR channels [J]. Phys Rev Lett, 1993, 70: 1895-1899.
(编辑:温文)
Demystifying quantum cryptography, quantum entanglement and quantum teleportation
SHI Yu
Department of Physics, Fudan University, Shanghai 200433, China
Exemplifed by the polarized states of photons, we make a concise, accurate and easily comprehensible introduction to the concepts of quantum mechanics, quantum states, quantum cryptography, quantum entanglement and quantum teleportation. First, the fundamental ideas of quantum mechanics and the meaning of quantum states are introduced through the comparison with classical physics. Then the BB84 scheme of quantum key distribution in quantum cryptography is explained. Afterwards, the concept of quantum entanglement is introduced, with the emphasis that it does not violate the theory of relativity. On the basis of this, quantum teleportation is explained, with the necessity of classical communication in the process emphasized.
quantum mechanics, quantum state, quantum cryptography, quantum entanglement, quantum teleportation
10.3969/j.issn.0253-9608.2016.04.002
†通信作者,E-mail: yushi@fudan.edu.cn

