提高试题难度的一种命题方法:换元
福建省泉州市第五中学
杨苍洲 (邮编:362000)
提高试题难度的一种命题方法:换元
福建省泉州市第五中学
杨苍洲 (邮编:362000)
在高中数学的命题工作中,选择、填空等题型的压轴试题的命制常常让命题者感到头疼.
如何才能迅速地命制出高质量的压轴试题呢?
笔者通过对一些高考压轴试题的研究,从中发现了一种命题方法——“换元法”.此种方法能有效地对试题进行包装,并快速提高试题的难度,是一种简单、高效的命题方法.
下面我们从命题的角度一起分析几道试题的命题思路,分享这种简单的命题方式.

命题思路探究
第一步:选定以三倍角公式cos3α=4cos3α-3cosα为背景命题.
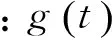
本题通过换元,进行巧妙的包装,隐去问题原本“三角函数”的真面目,得到一个新问题——含参数的三次函数恒成立问题.问题的解决必须以导数为工具进行求解,具有一定综合性,难度较大,适合于作为试题的压轴试题.
案例2 (2013年高考全国1卷改编)已知函数f(x)=(x2+x)(x2+ax+b),若对∀x∈R,有f(x)=f(2-x),则f(x)的最小值为( )
命题思路探究
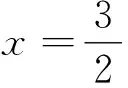

第四步:以函数y3的对称性为条件,设置参数,命成此题.
本题难度较大,是高考的压轴试题.问题的起点却是我们熟知的二次函数最值问题,经过命题者的巧妙构思、包装,隐去问题的本来面目,从而加大试题难度,提高试题的考查价值.
命题思路探究
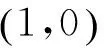
第二步:研究函数y=lnx与y=x-t的交点个数.可知,当t>1时,两个函数有两个交点.即方程lnx=x-t有两个实根.
本题貌似繁杂,实际上却是从重要不等式“lnx≤x-1”衍生而来.通过一步步的换元变换、化简运算、恒等变形,最终成题.在每一次变形中,都在不断地提高试题的难度、综合度,从而使得最终的问题具有较高的区分度.
体验了上述三道试题的命题心路历程,你应该也会赞叹“换元法”的神奇.“换元法”的确是一种高效的命题方法,你值得拥有!
2016-09-18)

