一类复合函数问题的图象解题法及启示
内蒙古师范大学附属中学
张 生 苏 猛 (邮编:611731)
一类复合函数问题的图象解题法及启示
内蒙古师范大学附属中学
张 生 苏 猛 (邮编:611731)
形如y=f[f(x)]的复合函数相关问题,在近几年的高考中屡见不鲜,(如2006年湖北理科、2009年福建理科第10题、2012年江苏理科第18题、2013年安徽理科第10题、2014年浙江理科第15题、2015年山东理科第10题等),常以压轴选择题或填空题的形式考查,相关资料对该类问题的解答通常为分类讨论,过程繁杂且不易于学生接受,更谈不上举一反三、触类旁通了.那么,如何获得解决该类问题的简洁而又通用的方法呢?经过对比研究,笔者从复合函数角度出发,利用换元思想,给出解决此类问题的一种通用图象解法(针对易画函数图象的问题).
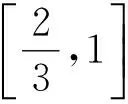

为了解决上述问题,我们可以先研究以下几个问题,为解题思路做必要的铺垫,以便更好地理解.
1 预设问题
问题1 函数y=f(x)(x∈R)和y=f(t)(t∈R)是不是同一函数?
设计意图 理解成为同一函数的两个基本要求:对应关系与定义域,而与自变量的表现形式无关.
问题2 能在同一坐标系中画两个函数图象吗?
设计意图 由于自变量表现形式不同,故可引导学生从不同的坐标系(分别在直角坐标系xOy和直角坐标系tOy中画图)中画函数图象,且图象应保持一致,为引例的解决做好铺垫.
问题3 函数y=f(t)和t=f(x)是不是同一函数,在不同直角坐标系下的图象是否一致?
设计意图 强化对同一函数要求的理解,应分情况讨论.另外,为将复合函数y=f[f(x)]利用换元思想写成函数y=f(t)和函数t=f(x)做准备.
2 图解引例
通过换元,借助函数y=f(t)和y=2t的图象可解决分解问题1(图1):

图1
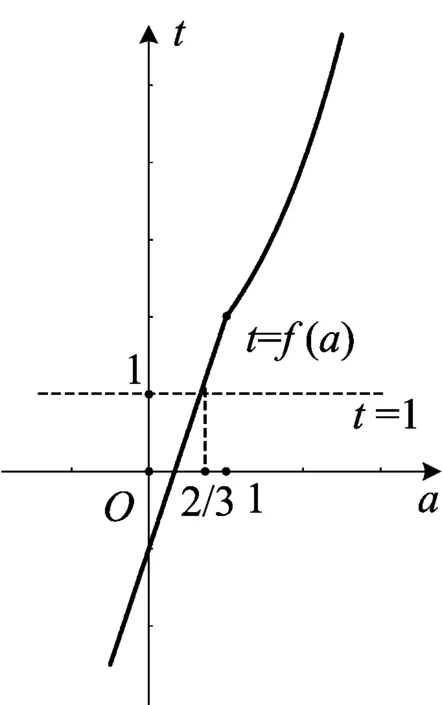
图2
由图1知,满足f(t)=2t的t的取值范围是t≥1,而t的取值范围与a的取值范围又有关联,即f(a)≥1.借助函数t=f(a)的图象解决分解问题2(图2):

综上,我们可归纳出解决该类问题的一般性方法:
(1)先进行换元,将复合函数y=f[f(x)]利用换元思想写成两个函数y=f(t)和t=f(x);
(2)分别在直角坐标系tOy和直角坐标系xOt中画出函数y=f(t)和t=f(x)的图象.这里需要说明的是,一般情况下,两幅函数图象应该不一致,只有当自变量t与自变量x的取值范围相同时,图象保持一致.但在具体作图中,未考虑自变量t与自变量x的取值范围,将两幅图画得完全一致,也不影响解题,请读者自行研究其原理.
(3)在直角坐标系tOy中,借助函数y=f(t)的图象求出t的范围(分解问题1),再在直角坐标系xOt中,利用函数t=f(x)的图象求出x的范围(分解问题2).
以上解法很好地回避了分类讨论过程,将整个解题过程以图形方式直观地呈现出来,易于学生理解与接受,同时注重了函数教学中需强化的数形结合思想.
3 变式与拓展
在解题教学中,应注重高效、通透的原则,可以设置有价值的问题串进行加深与拓展,从而提高教学质量,保证教学效果.
针对引例,我们可以设置如下问题:
设计意图 抓住问题实质,加深对解题方法的理解.
设计意图 将函数改为非单调函数,换元时应注意新变量的范围.
满足f{f[f(a)]}>2的a的取值范围是______.
设计意图 进行必要的拓展训练,深化解题方法的应用.鼓励学生勇于探究,敢于追问.
4 启示与感悟
如何提高学生的解题能力?如何培养学生的探究能力?应从解题策略的研究与指导开始,鼓励学生钻研问题,从根本上理解、吃透,方能达到举一反三、触类旁通之功效.同时,应重视培养学生养成良好的解题习惯,认真审题就是重要的好习惯.通过认真审题来搞清:条件有哪些,目标是什么,如何从条件出发达到目标,可以采用什么样的数学思想方法及技巧,解后反思、收获有哪些等,鼓励学生多从优化解题过程方面进行深入研究,以达到“做一题,通一类,带一片”的高效解题效应.

2016-09-12)

