对一道直线方程试题的探究
安徽省宁国中学
陈晓明 (邮编:242399)
对一道直线方程试题的探究
安徽省宁国中学
陈晓明 (邮编:242399)
这是笔者所在学校(省级示范高中)一道高三数学联考试题,这是一道填空题,考场上此题一部分同学答案是3,而另一部分同学答案是4.于是在试卷讲评课上笔者带领学生对该题解法一探究竟,以求找到不同答案产生的原因,掌握此类问题解题策略.结果同学们争论不休,课堂上精彩纷呈,生成不断,带来好多意外收获!
为了保持课堂的原汁原味,还是先回到课堂.
1 课堂实录
首先在黑板上展示题目:
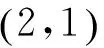
接下来教师让学生充分思考,动笔去解,老师在学生中巡视……
教师:谁来谈谈你的看法?
平时一直是心直口快的张同学首当其冲.
学生1(解法1:几何法):我的答案是4.我是通过画图来获得答案的.我觉得作为填空题用代数法太耗时了,不划算.
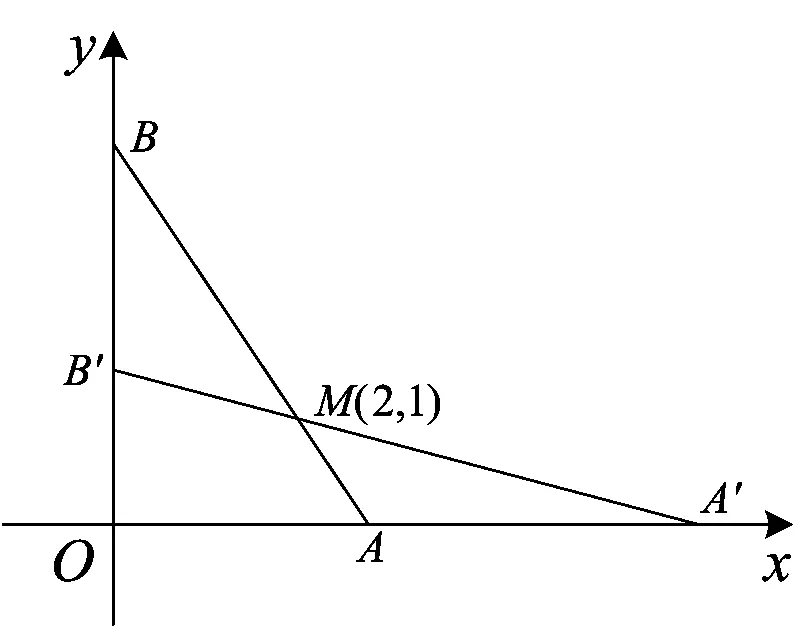
图1
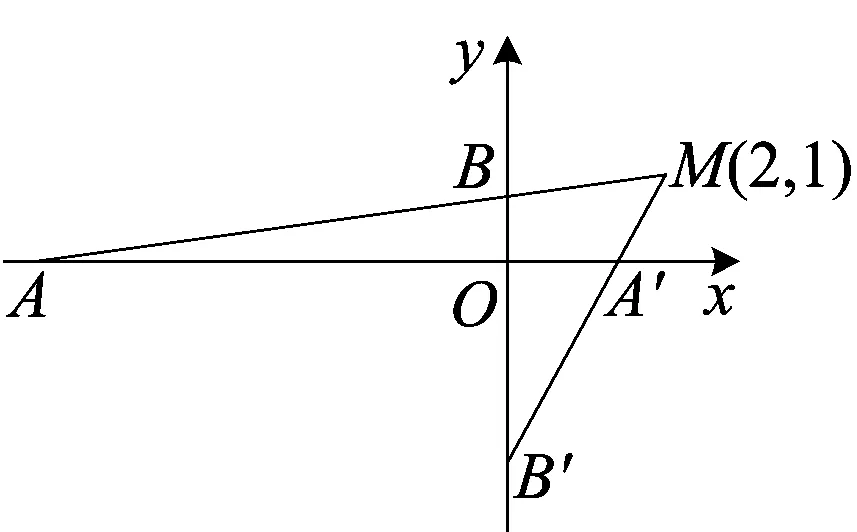
图2
令直线l的斜率为k(显然直线l的斜率存在),
如图1,当k<0时,有两种可能.
如图2,当k>0时,有两种可能.
因此共有4种可能,即这样的直线有4条.
许多学生表示支持,说自己当时也是这么做的.
就在这时,数学课代表说话了.
学生2(解法2:代数法):我用的是代数法,答案是3.
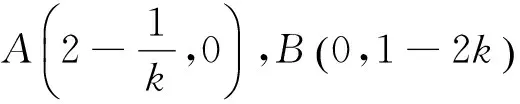
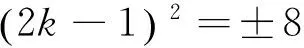
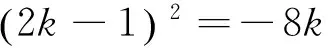


所以关于k的方程有两个不同的正实根.
由(1),(2)可知,k只有3个值,因此满足题意的直线应该有3条.
教师:两位同学分别用几何法和代数法获得了答案,很好!数学家华罗庚告诉我们“数缺形时少直观,形少数时难入微”,这句话充分肯定了数形结合的完备性,可是,今天“数”和“形”要“打架”了!问题出在哪儿呢?答案到底是3条还是4条?
“一石激起千层浪”,班上像炸开了锅,同学们陷入一片迷茫!分不清“哪个是孙悟空,哪个是六耳猕猴”?大家议论纷纷,争论不休……
过了好一会儿,班长站起来主持“公道”了.
学生3:我觉得答案应该是3条.
当k>0时,应该有2条,这个没有争议.
教师:厉害!那如果我们把4改为其它正数,答案又怎样?
班上同学们马上投入积极思考、计算中……课堂一片安静!
这时,平时不太爱说话的刘同学也被课堂气氛感染了,他也举手了.
学生4:我想起了我们前不久做过的一道题.
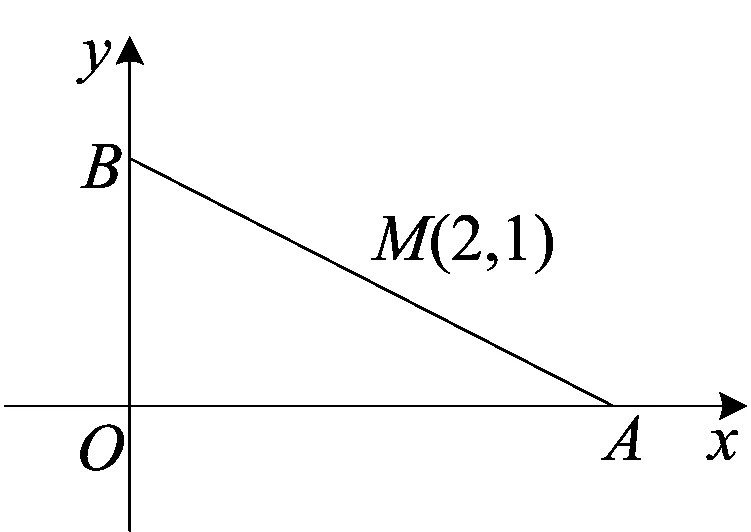
图3
我们当时还用了两种方法解.
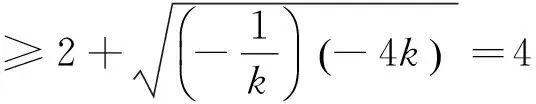
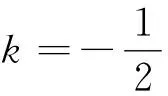
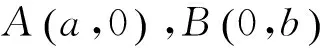
因此k<0时,因为本题中△AOB的面积的值为最小值4,故只有一条.k<0时,若△AOB的面积为小于4的正数时直线就没有,面积为大于4的正数时直线就有2条.
(对于该引例的进一步研究请参阅笔者发表在《上海中学数学》2015年第11期上的文章《关注新问题的生成,反思试卷讲评课的有效性》)
教师:你太聪明了!你真是不鸣则已,一鸣惊人!
内敛的刘同学高兴极了.
看到别人的成功,其余同学也都跃跃欲试.
班上有名的数学王子好像有了发现.
学生5:这题与课本上的一道题几乎完全相同,只是数字改变而已.
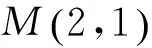
教师:纵观几十年的高考试题,信手可得到许多高考试题也来源于课本教材.教材中的例题习题具有典型性,示范性,同时也渗透着一些数学思想方法或提供某些结论.因此,以本为本,重视对教材中的例题习题的深入探究,是提高高考复习有效性的最佳捷径.另外,错解是宝,我们对错解仔细研究,就会拨开云雾见天日,洞察真相,认清本质.
学生心中的疑团解开了,个个露出满意的笑容,眼前豁然开朗起来!
就在我准备鸣锣收兵时,平时一向喜欢动脑的小朱同学举手了.
学生6:当k>0时一定有2条吗?
教师:提出问题比解决问题更重要.那大家看看,谁能从理论上证明这个结论吗?
很快有人举手了.
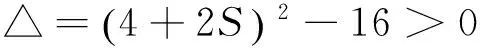
所以关于k的方程有两个不同的正实根.所以此时直线有2条.
教师:很好,又是一个数形结合.同学们在课后去研究一下k<0时的理论证明.
大家还能提出什么问题?
学生8:k<0时△AOB的面积的最小值应该与M点位置有关,有什么关系呢?
教师:对呀.这个问题很好,△AOB的面积的最小值能用M点坐标表示吗?
在此结论留给读者探究,不再赘述.(同样可参阅前面提到的笔者的那篇论文)
教师:以后出现类似题目,当给出M点坐标,我们就可判断当k<0,时△AOB的面积的最小值,从而可根据给的面积的值推断直线有几条了.当然也可用前面的代数法.不能就通过画简图而轻易下结论,否则容易出错.
就在我话刚讲完,学习委员迫不及待地举手了.
学生9:老师,您说的有些不对.上述结论只有当M点位于第I,III象限时成立,此时只有当k<0时,△AOB的面积能取最小值.如果当M点位于第II,IV象限时,只有k>0时,△AOB的面积能取最小值.
教师:高手!你比老师我还强!真是“青出于蓝胜于蓝”,我还真没想到.(此时课堂响起了掌声!)
接下来又有同学提出了一些问题,大家一同进行了研究.
教师:大家由此题的研究得到什么启示?
学生七嘴八舌,概括起来主要是下面几点:
①所研究问题与以前的哪些问题相类似,解决此类问题的基本思路是什么?
②解题的关键在哪里?是如何化归的?
③本题是否有别的解法?有无更好的解法?
④哪一种方法最基本、最典型?哪一种最简便?哪一种最巧妙?
⑤解题结果是否正确、圆满?有无增、漏、错等情况?
⑥命题的逆命题是否成立?此命题能否进行变式、引申和拓展?
⑦解题中运用了哪些数学思想方法?以前是否运用过这些数学思想方法?有何联系与区别?是否具有规律性?
此时下课铃声响起!
我看到了学生脸上的表情:惊叹之余,有些不舍和遗憾!
2 教学思考
“灯不挑不明,理不辩不清”,我们教师要充分利用学生的错误资源,给学生多一些思考,多一些争论.要充分相信学生,不能只按照自己事先想好的思路来教学,否则就会限制学生的思维,强扭学生的思维.题目刚出来就先进行提示或分析,那样做会扼杀学生的自主思维能力,剥夺学生的自由创造空间.在学生还没来得及思考的时候,老师硬是用自己固定的思路框定他们的头脑,使他们服从于已有的模式,这对他们思维能力的形成是个不小的打击.
离开了学生的“自主活动”、“智力参与”、“个人体验”就没有真正的学习了.把课堂还给学生,引发学生积极思维,让每位学生在数学思维的世界里自由地翱翔,向习题课教学要效益,通过问题解决,促进学生对数学知识的理解,让每位学生主动、积极地参与教学.当然,要做到这点,首先教师对习题的本身要有深入的研究;其次,对学生的课堂参与要给予足够的激励和引导.把课堂还给学生,注意倾听他们的声音,点燃他们思维之火.
到这里,我想起叶澜教授曾说:“课堂是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的因素,而不是一切都必须遵循固定路线而没有激情行程.”
3 结束语
陶哲轩在《解题·成长 ·快乐》序言中引用古希腊哲学家普罗克洛斯的话:“这,就是数学:她提醒你灵魂有不可见的形态;她赋予自己的发现以生命;她唤醒悟性,澄清思维;她照亮了我们内心的思想;她涤尽我们有生以来的蒙昧与无知……” .笔者以此与各位同仁共勉!在数学中让我们永远带着探寻的目光审视眼前的一切,一定会有惊喜出现!
1 刘飞.2014年高考数学安徽卷理科第16题的探究[J].中学数学教学,2014(4):43
2 陈晓明.我教书,我写作,我快乐[J].数学通讯,2016(5):39
3 张晓东.说题与数学青年教师的专业成长[J].中学数学教学参考,2015(3):67
2016-10-09)

