分数阶电路阶跃响应特性研究

王志兰

（山西大学电力工程系，太原,030013）

分数阶电路阶跃响应特性研究

王志兰

（山西大学电力工程系，太原,030013）

针对分数阶动态电路，基于分数阶微分方程的解析解，研究0~2阶分数阶动态电路的阶跃响应。利用MATLAB软件，得到不同阶次分数阶电路的阶跃响应曲线，并与整数一阶电路和二阶电路的阶跃响应作了对比研究，为今后分数阶电路的研究奠定了基础。

分数阶电路；解析解；阶跃响应

0 引言

分数阶微积分是指阶次为分数的微积分，当阶次为整数时，等同于常规定义下的微积分运算。学者们认为，当前对电容和电感的整数阶物理描述是理想模型，分数阶的描述才是更真实的，本文将基于分数阶来研究动态电路的响应。

求解分数阶系统，解析算法有拉氏变换法和傅里叶变换法，数值算法有Zhang and Shimizu法，L-1法和池田法等。数值算法虽然编程简单，但计算精度取决于时间步长，若时间步长太小，计算时间过长。本文采用解析算法，精度较高，且所选系统为两项分数阶系统，大大降低了解析算法公式的复杂度。

1 两项分数阶微分方程的解析解

初值为零的两项分数阶微分方程为：

根据Podlubny的理论[4]和文献[5]和[6]对两项分数阶微分方程的研究，给出上式的解析解：

2 分数阶动态电路

2.1 含一个分数阶元件的动态电路

以RC串联电路为例，研究分数阶电抗的阶跃响应。设分数阶电容的阶次为α∈(0,1)，以uc(t)为待求量，对应的微分方程为：

设电容初始储能为零，即uc(0-)=0；为简化方程，令R=1Ω，C=1F，当u(t)=时，利用MATLAB编程仿真，求得不同时电容电压的单位阶跃响应，如图1。α=1时为整数阶电路。

由仿真结果可以看出，随着分数阶电容阶次的增大，稳定输出增大，响应时间也增大。阶次低于1时，响应曲线未出现振荡，与一阶系统的阶跃响应曲线走向一致，但稳定输出小于1。

图1 不同阶次分数阶动态电路的单位阶跃响应

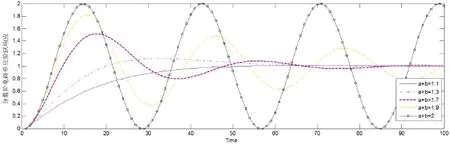
图2 阶次为1-2阶电路的阶跃响应

2.2 含两个分数阶元件的动态电路

用分数阶电感和分数阶电容元件并联形成含两个分数阶元件的动态电路，电容和电感的阶次分别为

α∈(0,1)和β∈(0,1)。以iL(t)为待求量，对应的方程为：

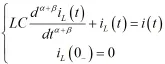
求解上式，得到不同阶次的分数阶电感和分数阶电容组成的无阻尼电路的单位阶跃响应，α+β＜1时同上分析，只分析α+β＞1的情况，结果如图2。

可以看出，当阶次大于1时，阶跃响应开始出现振荡，且随着阶次增大，振荡加剧，直至2阶系统的等幅振荡阶跃响应；同时，阶次增大，达到稳态的时间变长，最大超调量变大。

3 结论

本文从拉氏变换的角度给出了分数阶微分方程的解析解，分析了阶次在0-2之间的分数阶电路的单位阶跃响应，与传统整数阶电路作了对比研究。研究表明分数阶系统可取得比整数阶系统更灵活的响应输出和响应时间，可利用分数阶元件实现对整数阶系统的改进。

[1]周激流，蒲亦非，廖科．分数阶微积分原理及其在现代信号分析与处理中的应用[M]．北京：科学出版社，2010．

[2]汪纪锋.分数阶系统控制性能分析[M]．北京：电子工业出版社，2010．

[3]王振滨，曹广益．分数阶动态系统的数值算法[J]．系统仿真学报，2004，16(3)：477-479，484．

[4]Podlubny I．Fractional Differential Equations[M]．San Diego：Academic Press，1999．

[5]王学彬．两项分数阶微分方程在控制系统的应用[J]．南平师专学报，2005，24(2)：16-19．

[6]Yizheng Hu，Yong Luo，Zhengyi Lu．Analytical solution of the linear fractional differential equation by Adomian decomposition method[J]．Computational and Applied Methematics，2008，215(1)：220-229．

Research on the Step Response Characteristics of Fractional Order Circuit

Wang Zhilan
(Department of Power Engineering,Shanxi University,Taiyuan,030013,China)

Based on the analytic solution of fractional differential equations,the paper investigates the step responses of fractional circuit with the order between zero and two.The simulation results are compared with the step responses of integer order circuit.This paper lays the foundation for the future research of the fractional order circuit.

fractional circuit;analytic solution;step response