样例设计及呈现方式对学习代数运算规则的促进*

杜雪娇 张 奇

(辽宁师范大学心理学院, 大连 116029)

1 问题提出

样例学习(worked-example learning)是学生在已有知识经验的基础上, 通过阅读和思考样例, 领悟新的知识、概念或规则, 并掌握其应用的过程(Bourne, Goldstein, & Link, 1964)。

在有关“专家”和“新手”问题解决能力的差异研究中发现, 专家和新手在解决下棋、几何、代数、物理等问题上存在明显的差异(Chase & Simon,1973; Sweller & Cooper, 1985)。产生差异的主要原因是专家比新手拥有更多相关领域的知识结构或图式, 因此他们更关注问题的结构特征, 进而加快了对问题的理解(Carroll, Galegher, & Wiener,1982)。由于单纯的问题解决练习的形式本身不利于初学者问题解决图式的习得, 所以, 研究者们开始关注如何通过问题解决的样例学习来提高新手的问题解决能力, 进而促进了关于问题解决样例学习的研究(Anderson & Fincham, 1994; Renkl,Atkinson, Maier, & Staley, 2002)。对于学生尤其是新手来说, 与传统的问题解决方式相比, 样例学习的效果更好、效率更高, 即学生投入较少的时间和心理资源就能获得较好的学习效果(Bokosmaty,Sweller, & Kalyuga, 2015)。

在问题解决样例的学习中, 学生能否正确理解和掌握其中的原理或规则, 制约着样例学习的效果(Wynder & Luckett, 1999)。因此, 在样例设计中, 如何引导学生根据具体的问题情境, 掌握并运用具体的解题规则是非常重要的(Renkl, Hilbert, & Schworm,2009)。

上述研究表明, 问题解决的样例学习可以提高学生问题解决的能力, 尤其可以帮助新手尽快掌握问题解决的图式及其运用。除此之外, 经过样例学习还可以使学生领悟样例中隐含的新规则并学会新规则的应用。Anderson和Fincham (1994)的实验表明, 被试在学习包含产生式规则的样例后, 均能通过分析样例, 发现并学会使用该规则。Lee和Chen (2015)的研究中借助计算机程序设计了学生可以进行虚拟操纵的样例, 证实了这种样例学习能帮助五年级小学生更好地理解等分数的概念和规则, 并提高了学生的学习兴趣。大量研究(Clarke,Ayres, & Sweller, 2005; Richey & Nokes-Malach,2013; Seufert, 2003; 许德志, 张奇, 2011; 张奇, 郭菲菲, 2008; 张奇, 林洪新, 2005; 张奇, 张华, 2014)从数学、物理、化学等各个知识领域验证了学生在学习了包含某种新规则的样例后, 能够发现并运用其中的新规则。总体来说, 这些研究侧重于采用一些设计良好的样例, 让被试利用已有的相关基础知识, 从样例中发现新规则并学会新规则的运用。这就是规则样例学习的研究。

在数学运算规则样例学习的研究中, 张奇和林洪新(2005)的研究发现, 经过样例学习, 二年级小学生能够领悟四则混合运算规则。张奇和郭菲菲(2008)的研究表明, 三至五年级小学生可以不同程度地学会运用“去括号”运算规则。Adams等人(2014)的研究也发现, 通过辨别、改正错误等样例的学习,能使学生更加深入地理解小数的概念, 并领悟小数的大小和递加运算规则。

可是, 在小学生代数运算规则样例学习的研究中却遇到了问题(林洪新, 张奇, 2007)。该研究采用“完整”或“不完整”的样例设计以及在不完整样例的学习中给予反馈或无反馈的学习程序, 考察了六年级小学生学习“平方差”与“完全平方和”的代数运算规则的效果。实验结果显示, 多数被试难以学会“平方差”运算规则, 只有少数被试学会了“完全平方和”运算规则。究其原因, 一方面可能是不完整样例的设计方法增加了学生理解和领悟代数运算规则的难度, 妨碍了学习; 另一方面可能是小学生不理解代数运算样例中“a”、“ab”等代数运算符号的含义, 或不熟悉在代数运算中加、减同类项等代数运算策略的意义。因此, 研究者就如何设计样例以帮助学生领悟新算符和新的运算规则的含义进行了探索。

张奇等人经过对数学运算规则之间逻辑关系的考察后发现, 新的或学生未知的数学运算符号或运算规则都可以用学生已知的运算符号或规则来表示, 并提出了在数学运算样例中设计新算符或新运算规则的“解释法”。所谓的“解释法”就是将新的运算规则或新算符用学生已知的运算规则或算符来加以解释(张奇, 蔡晨, 2015)。例如, “a”可以用“a=a × a”来表示, “ab”可以用“ab=a × b”来表示,以帮助学生理解“a”、“ab”的运算含义。随后, 又提出了新算符和新规则样例设计的“标记法”和“转换标记法” (张华, 曲可佳, 张奇, 2013)。所谓的“标记法”就是将新算符和新规则的数学解释内容加上醒目的颜色或标记, 以增强学生对解释内容的注意和理解。“转换标记法”就是用连线标记出转换运算样例中运算步骤之间或变量之间的对应关系。该研究分别采用“转换标记法”和“解释法”设计了“指−对数转换”运算和对数运算的样例。并通过实验验证了“解释法”和“转换标记法”样例均能帮助学生理解新算符和新规则的含义, 与普通样例相比, 明显提高了样例学习的效果。接着, 张奇、郑伟和万莹(2014)的研究又证明了“解释法”和“解释−标记法”样例设计对小学生学习分数运算规则和比例运算规则的促进作用。其中的“解释−标记法”是“解释法”和“标记法”的结合。

尽管, 张奇等人在实验中(张华等, 2013; 张奇等, 2014)证明了“解释法”、“转换标记法”和“解释−标记法”的有效性, 即这些方法的样例设计对被试领悟新算符和新规则的促进作用。但是, 这些实验中所采用的运算样例都是算术运算样例, 而不是代数运算样例。例如, 在“指−对数转换”运算样例和对数运算样例中只是出现了对数符号“log”, 在分数运算和比例运算中也都是算术运算样例。而采用“解释法”和“解释−标记法”设计代数运算的样例是否能够起到同样的促进作用, 还没有得到实验的验证。具体来说, 采用这些方法设计代数运算的样例究竟能否促进小学生学会“完全平方和”和“平方差”代数运算规则, 还有待实验的证实。因为, 代数运算与算术运算有以下主要的不同：(1)算术运算是数值运算, 可以算出数值结果; 而代数运算是符号运算, 只能得出代数式。(2)算术运算与代数运算的运算符号不尽相同, 算术运算中的“2乘以3”写作“2 ×3”, 而代数运算中的“a乘以b”写作“ab”。(3)代数乘法运算必须遵循“交换律”和“分配律”, 例如, “ab=ba”、“ab + ba=2ab”以及“(a + b)=a (a + b) + b (a +b)=a+ ab + ba + b=a+ 2ab + b”。而算术运算却不必如此繁琐, 例如, “(2 + 3)=5=25”和“(3 + 2) ×(3 – 2)=5 × 1=5”。(4)代数和算术的运算策略不同,例如, 要想证明“a– b=(a + b) (a – b)”, 必须在“a– b”算式中加入“+ab”和“–ab”两项, 即“a– b=a+ ab – b– ab=a (a + b) – b (a + b)=(a + b) (a –b)”,才能证明“a– b=(a + b) (a – b)”成立。而在算术运算中则是“3– 2=9 – 4=5”或者“(3 + 2) × (3 –2)=5 × 1=5”, 用“ 3– 2=(3 + 2) × (3 – 2)=5”直接就可以证明。所以, 为了证明上述的样例设计方法在数学运算样例学习中有促进作用, 必须证明它们既在算术运算样例学习中有促进作用, 而且在代数运算样例学习中也有促进作用。之所以这样做,其目的就在于证明上述样例设计方法是在数学运算样例设计中普遍适用的方法和有普遍促进作用的样例设计方法。

因此, 分别采用“解释法”和“解释−标记法”设计“完全平方和”和“平方差”的代数运算样例, 仍然以六年级小学生为被试, 并与普通样例比较, 考察其样例学习的效果。实验1采用“解释法”设计了这两种代数运算规则的样例, 并考察其学习效果是否优于普通样例的学习效果。实验2采用“解释法”和“解释−标记法”设计两种代数运算的样例, 并考察“解释−标记法”样例的学习效果是否比“解释法”样例更好。值得注意的是, 以往的研究中“标记”的运用往往只涉及一个或几个运算步骤, 这样的标记比较简洁清晰, 能起到明显的提醒注意和促进思考的作用。而该研究中所采用的“解释−标记法”对每步运算与下一步运算的转换对应关系均进行了标记。所以, 标记较多, 可能会增加被试的外在认知负荷,降低学习效果。有研究表明样例呈现方式也会影响样例学习效果, 诸如逐步渐减呈现不完整样例(Renkl & Athinson, 2003)、相继呈现双内容样例(Clark et al., 2005)、分段呈现动态样例(Spanjers,Wouters, van Gog, & van Merriënboer, 2011)等方式均能降低学习过程中的认知负荷, 提高学习效果。所以, 实验3将分步呈现“解释−标记”样例的学习效果与整体呈现样例的学习效果进行比较。所谓“分步呈现”是每次只呈现样例的一个运算步骤及其转换标记, 待被试学习理解后再呈现下一个运算步骤, 直至学习完整个样例。这样可能会降低学生样例学习的认知负荷, 并提高学习效果。而整体呈现就是一次性呈现运算样例的所有运算步骤、运算标记和运算结果。实验假设是分步呈现的学习效果可能优于整体呈现的学习效果。

2 实验研究

2.1 实验1 “解释法”样例设计对代数运算规则学习迁移效果的促进作用

2.1.1 实验目的

考察采用“解释法”设计的“完全平方和”和“平方差”代数运算样例, 其学习迁移成绩是否显著优于普通样例的学习迁移成绩。

2.1.2 被试

通过“前测”从潍坊市一所普通小学(奎文区实验小学)的六年级学生中筛选出120名被试。其中,男生60人, 女生60人。将其随机分为4组, 每组30人。

2.1.3 实验材料

前测材料：用来筛选被试, 共有6道题。前2道题是一位数的平方运算题, 第3道题和第4道题分别是乘法交换律和分配律代数运算题, 后2道题根据实验分组的不同而不同：“完全平方和”运算样例组(第一组与第二组)为2道“完全平方和”代数运算题; “平方差”运算样例组(第三组与第四组)为2道“平方差”代数运算题。只有在“前测”中能够正确计算出前4道题, 且不能正确计算出后两道题的小学生才能成为正式实验的被试。由于学习“完全平方和”或“平方差”代数运算规则要以掌握平方、乘法交换律和分配律为基础, 因此实验要求的被试必须是准确掌握上述基础知识, 且尚没有掌握“完全平方和”或“平方差”代数运算规则的学生。

样例学习材料：分为4种, 每种包含2道样例。第一种是普通的“完全平方和”代数运算样例; 第二种是采用“解释法”设计的“完全平方和”代数运算样例; 第三种是普通的“平方差”代数运算样例; 第四种是采用“解释法”设计的“平方差”代数运算样例。“完全平方和”和“平方差”两种运算样例与林洪新和张奇(2007)的研究中的完整样例相同。“解释法”样例设计是用学生已知的运算规则或算符对“(a +b)”、“合并同类项”等新运算符号或运算规则做出了“算式解释”。“解释法”样例与普通样例只是运算步骤的设计不同, 其他均相同。

迁移测验材料：包括“完全平方和”运算规则测验材料和“平方差”运算规则测验材料。均由6道迁移测验题组成。其中, 前3道是近迁移测验题, 后3道是远迁移测验题。近迁移测验题与样例题的字母不同, 运算结构相同; 远迁移测验题与样例题的字母和运算结构均不同。被试正确完成1道测题记1分, 远、近迁移测验满分均为3分。

在正式实验中, 前测材料、样例学习材料和迁移测验材料及相应的指导语分别在A4纸上呈现,字体为宋体、四号、加粗、1.5倍行距。

2.1.4 实验设计

采用2(规则类型)× 2(样例类型)二因素被试间随机分组实验设计。规则类型分为“完全平方和”和“平方差”两种代数运算规则; 样例类型分为普通样例和“解释法”样例。因变量为远、近迁移测验成绩。

2.1.5 实验程序

前测阶段：“前测”在安静的教室内进行。主试首先向各组待选被试发放相应的前测试卷, 并说明前测时间为8 min。8 min后, 收回前测试卷。选择能够正确计算出前4道题, 但不能正确计算出后两道题的被试进入下面的实验。

样例学习阶段：各组被试分别在不同的教室里同时学习相应的样例学习材料。样例学习时间为15 min。15 min后, 主试收回样例学习材料。

迁移测验阶段：给各组被试呈现对应的迁移测验试卷。测验时间为20 min。20 min后, 主试收回测试材料。

2.1.6 结果分析

各组被试的远、近迁移测验成绩见图1。

二因素方差分析结果显示, 近迁移测验成绩在两种规则类型之间差异显著,

F

(1, 116)=20.55,

p

<0.001, η=0.15; 在两种样例类型之间差异显著,

F

(1, 116)=10.01,

p

< 0.01, η=0.08; 规则类型和样例类型对近迁移测验成绩的交互作用不显著,

F

(1, 116)=0.01,

p

> 0.05。远迁移测验成绩在两种规则类型之间差异显著,

F

(1, 116)=9.42,

p

< 0.01,η=0.08; 在两种样例类型之间差异显著,

F

(1, 116)=5.47,

p

< 0.05, η=0.05; 规则类型和样例类型对远迁移测验成绩的交互作用不显著,

F

(1, 116)=1.05,

p

> 0.05。

上述实验结果表明, 与普通样例的学习迁移成绩相比, “解释法”样例设计明显提高了六年级小学生学习“完全平方和”与“平方差”代数运算规则的迁移成绩, 即证明了“解释法”样例设计的有效性和优越性。接下来的实验2考察“解释−标记法”样例设计对两种代数运算规则样例学习的促进作用。

2.2 实验2 “解释−标记法”样例设计对代数运算规则学习迁移效果的促进作用

2.2.1 实验目的

考察学习采用“解释−标记法”设计的“完全平方和”和“平方差”代数运算样例是否比学习采用“解释法”设计的样例更能提高学习迁移成绩。

2.2.2 被试

通过“前测”从潍坊市一所普通小学(幸福街小学)的六年级学生中筛选出120名被试。其中, 男生58人, 女生62人。将其随机分为4组, 每组30人。

2.2.3 实验材料

前测材料：同实验1。

样例学习材料：分为4种, 每种包含2道样例：第一种是采用“解释法”设计的“完全平方和”代数运算样例; 第二种是采用“解释−标记法”设计的“完全平方和”代数运算样例; 第三种是采用“解释法”设计的“平方差”代数运算样例; 第四种是采用“解释−标记法”设计的“平方差”代数运算样例。采用“解释−标记法”设计的样例是在“解释法”的基础上, 用红色箭头对前后运算步骤间的转换对应关系进行标记。

迁移测验材料：同实验1。

在正式实验中, 前测材料、样例学习材料和迁移测验材料及其指导语分别在A4白纸上呈现, 字体为四号宋体字、加粗、1.5倍行距。

2.2.4 实验设计

采用2(规则类型)× 2(样例类型)二因素被试间随机分组实验设计。规则类型分为“完全平方和”和“平方差”两种代数运算规则; 样例类型分为“解释法”样例和“解释−标记法”样例。因变量为远、近迁移测验成绩。

2.2.5 实验程序

前测阶段：同实验1。

样例学习阶段：各组被试分别在不同的教室里同时学习相应的样例学习材料。学习的时间为15 min。15 min后, 收回样例材料。

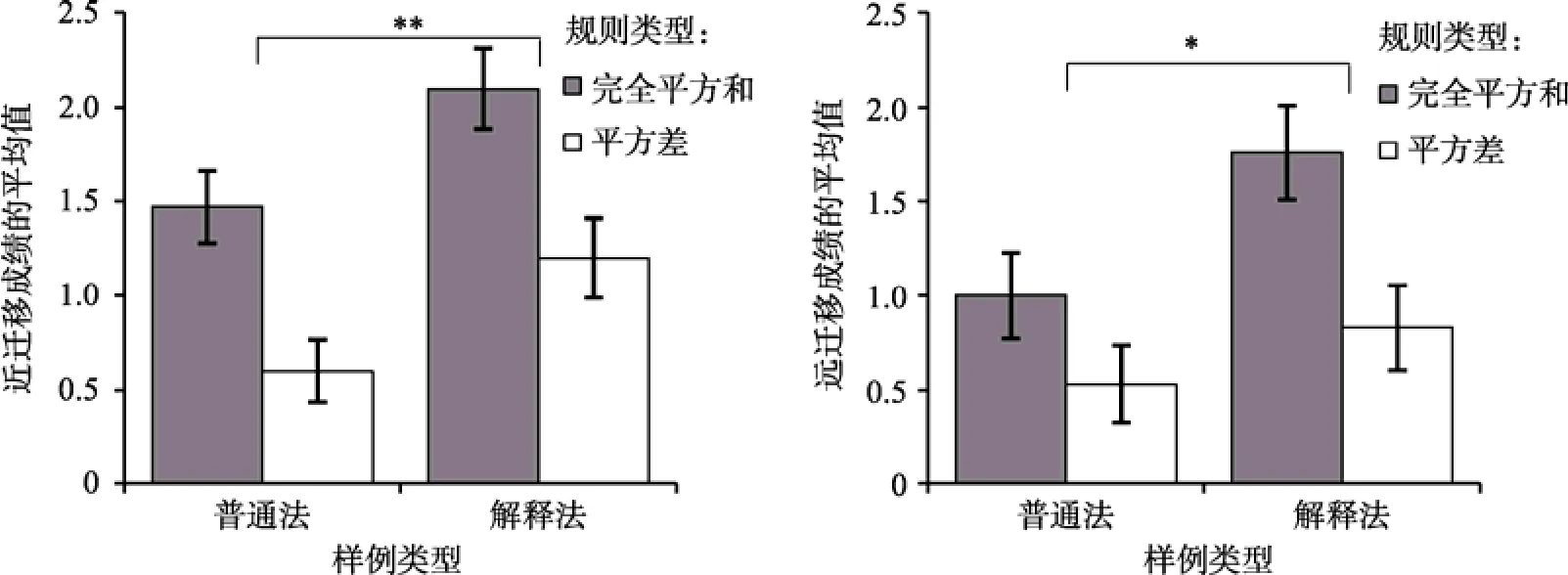
图1 各组被试远、近迁移测验成绩及差异检验结果

迁移测验阶段：同实验1。

2.2.6 结果分析

各组被试迁移测验成绩见图2。

二因素方差分析结果显示, 近迁移测验成绩在两种规则类型之间差异显著,

F

(1, 116)=5.39,

p

<0.05, η=0.04; 在两种样例类型之间差异显著,

F

(1,116)=4.67,

p

< 0.05, η=0.04; 规则类型与样例类型对近迁移成绩的交互作用显著,

F

(1, 116)=4.01,

p

< 0.05, η=0.03。简单效应分析结果显示, 在“完全平方和”运算规则上, “解释法”样例与“解释−标记法”样例的近迁移成绩差异不显著,

F

(1, 117)=0.01,

p

> 0.05; 在“平方差”运算规则上, “解释−标记法”样例的近迁移成绩显著优于“解释法”样例的近迁移成绩,

F

(1, 117)=8.35,

p

< 0.01, η=0.07。在“解释法”样例中, “完全平方和”的近迁移成绩显著优于“平方差”的近迁移成绩,

F

(1, 117)=9.06,

p

<0.01, η=0.08; 在“解释−标记法”样例中, “完全平方和”与“平方差”的近迁移成绩差异不显著,

F

(1,117)=0.05,

p

> 0.05。两种规则类型的远迁移成绩差异显著,

F

(1,116)=9.01,

p

< 0.01, η=0.07; 两种样例类型间的远迁移成绩差异不显著,

F

(1, 116)=1.41,

p

> 0.05;规则类型与样例类型对远迁移成绩的交互作用不显著

F

(1, 116)=0.82,

p

> 0.05。

实验2的结果表明, 在学习“解释−标记法”样例的迁移测验成绩中, 只有学习“平方差”运算规则的近迁移成绩上明显优于学习“解释法”样例的近迁移成绩, 而其他迁移成绩在两种样例之间差异均不显著。这说明“解释−标记法”样例设计对小学生学习两种代数运算规则的促进作用并不十分显著。如何进一步发挥“解释−标记法”样例设计的促进作用呢？为此进行了下面实验3的研究。

2.3 实验3分步呈现“解释−标记法”样例对代数运算规则学习迁移效果的促进作用

2.3.1 实验目的

在“解释−标记法”的基础上, 设计了两种样例呈现方式：一种是分步呈现; 一种是整体呈现。考察这两种呈现方式对“完全平方和”和“平方差”代数运算规则样例学习迁移成绩的影响。

2.3.2 被试

通过“前测”从潍坊市一所普通小学(高新双语学校)的六年级学生中筛选出120被试。其中, 男生59人, 女生61人。将其随机分为4组, 每组30人。

2.3.3 实验材料

前测材料：同实验1。

样例学习材料：分为4种, 每种包含2道样例：第一种是整体呈现的“完全平方和”代数运算样例;第二种是分步呈现的“完全平方和”代数运算样例;第三种是整体呈现的“平方差”代数运算样例; 第四种是分步呈现的“平方差”代数运算样例。整体呈现的样例同实验2中采用“解释−标记法”设计的样例一样, 所有步骤及其转换标记同时呈现。“分步呈现”即首先呈现第一步及该步的转换标记, 当被试看明白后, 即可点击“下一步”按钮, 第一步的转换标记消失, 呈现第二步及其转换标记, 被试也可通过点击“上一步”按钮, 返回查看上一步的转换标记。以此类推, 直至被试查看完并学会样例的所有步骤。实验前主试通过指导语向被试介绍这种分步呈现过程和“上一步”“下一步”按钮的使用。图3为采用分步呈现的“完全平方和”运算样例的截屏。

迁移测验材料：同实验1。

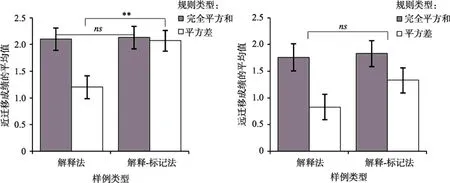
图2 各组被试远、近迁移测验成绩及差异检验结果

在正式实验中, 前测材料、迁移测验材料及其指导语在A4白纸上呈现, 样例学习材料及其指导语在电脑显示器上呈现, 字体均为宋体四号字, 1.5倍行距。

图3 分步呈现的“完全平方和”运算样例学习材料截屏

2.3.4 实验设计

采用2(规则类型)× 2(呈现方式)二因素被试间随机分组实验设计。规则类型分为“完全平方和”和“平方差”两种代数运算规则; 呈现方式分为“整体呈现”和“分步呈现”两种方式。因变量为远、近迁移测验成绩。

2.3.5 实验程序

前测阶段：同实验1。

样例学习阶段：4组被试分别在不同的教室里使用电脑显示器同时学习各自的样例学习材料。学习时间限定为15 min, 15 min后进行迁移测验。

迁移测验阶段：同实验1。

2.3.6 结果分析

各组被试的迁移测验成绩见图4。

二因素方差分析结果显示, 近迁移测验成绩在两种规则类型之间差异不显著,

F

(1, 116)=0.07,

p

>0.05; 在两种呈现方式之间差异显著,

F

(1, 116)=8.85,

p

< 0.01, η=0.07; 规则类型和呈现方式对近迁移测验成绩的交互作用不显著,

F

(1, 116)=0.01,

p

> 0.05。远迁移测验成绩在两种规则类型之间差异显著,

F

(1, 116)=4.51,

p

< 0.05, η=0.04; 在两种呈现方式之间差异显著,

F

(1, 116)=8.16,

p

<0.05, η=0.07; 但规则类型和呈现方式对远迁移测验成绩的交互作用不显著,

F

(1, 116)=0.01,

p

> 0.05。

实验3的结果表明, 学习“分步呈现”的两种代数运算规则的“解释−标记”样例的远、近迁移测验成绩均明显优于学习“整体呈现”的两种代数运算规则的“解释−标记”样例的远、近迁移测验成绩。这说明“分步呈现”方式对“解释−标记”样例的学习迁移效果有明显的促进作用。

3 讨论

3.1 “解释法”样例对代数运算规则学习迁移效果的促进作用

在样例设计中给被试提供多少“解释”以及如何提供这些“解释”才能优化学习过程、提高学习效果, 一直以来都是研究者广泛关注的问题(Koedinger& Aleven, 2007; Richey & Nokes-Malach, 2013;Wittwer & Renkl, 2010)。在以往的研究中, 有人设计了含有指导性解释(instructional explanation)的样例和“过程导向” (process-oriented)的样例。含有指导性解释的样例是对样例中的每一个运算步骤的目的和原理都进行解释(Renkl et al., 2009)。“过程导向”的样例是在呈现问题解决方案的同时, 对解决方案的原理加以解释, 并呈现策略信息的样例(van Gog, Paas, & van Merriënboer, 2008)。而且, 它们都是在运算样例中附加的文字解释。这样的样例设计对于初学者来说, 确实具有易学、易懂、快捷、有效的作用, 不失为一种有效的解释方法。可是, 这种解释降低了样例学习的难度, 对于那些数学学习能力较强和具有挑战精神的学生来说, 有些过于简单, 并有可能降低这些学生自主探究的学习兴趣和动机水平。而且这种样例的学习效果也存在争议(Renkl et al., 2009; Schworm & Renkl, 2006; Wittwer& Renkl, 2010)。

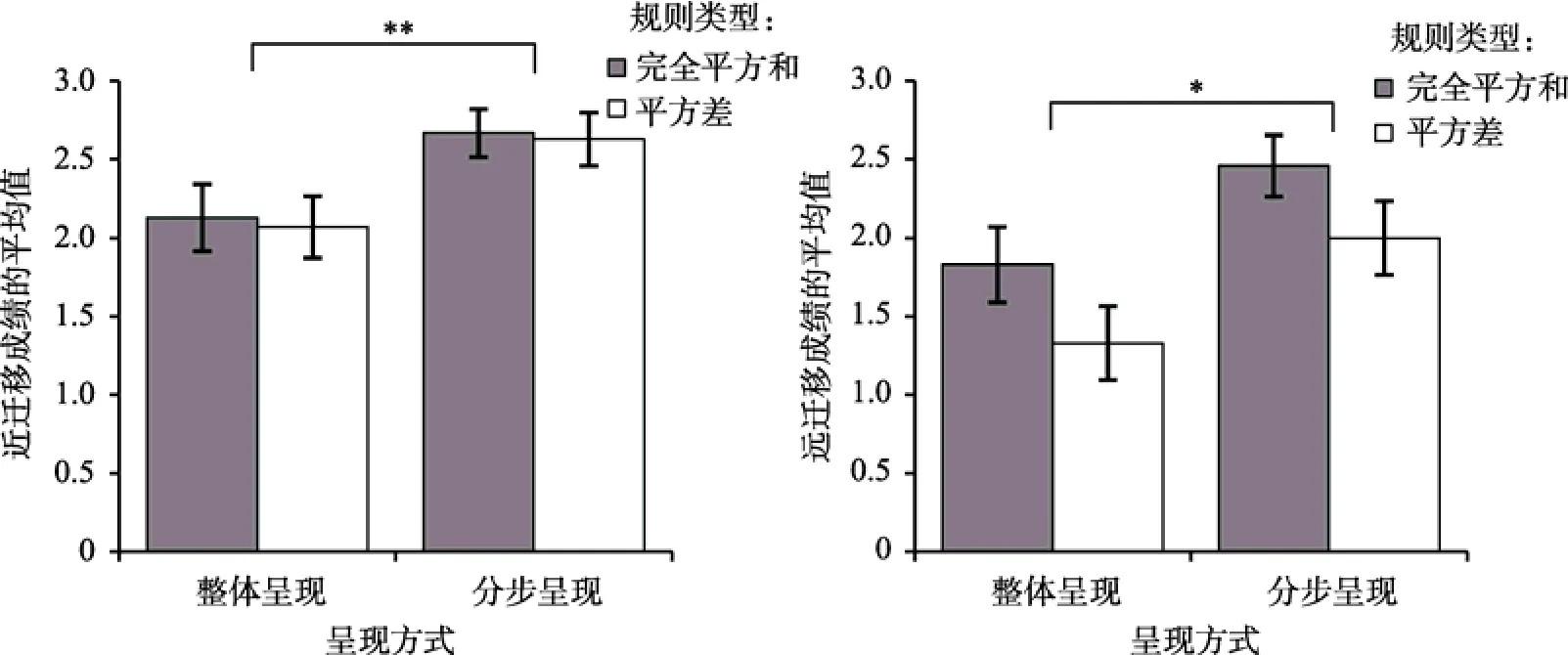
图4 各组被试远、近迁移测验成绩及差异检验结果

不同于这种文字解释, 张奇等人提出的“解释法”是一种“算式解释法”或“数学解释法” (简称为“解释法”)。这种“解释”是用学生已知的算符和运算规则在运算样例中“解释”新算符的运算含义和新运算规则的运算步骤, 而且是一种直接运用数学语言的解释。采用这种解释法设计的运算样例突显了数学语言的运用, 有助于培养学生的抽象逻辑思维。由于学习这种样例的难度大于用文字解释的样例, 所以它更能激发学生的自主探究精神、学习兴趣和动机水平。实验1的结果表明, 学习“解释法”样例后的远、近迁移测验成绩均明显优于学习普通样例的迁移测验成绩。这就足以说明, 该种解释方法明显地促进了初学者对新算符(如“a”、“ab”)以及“完全平方和”、“平方差”代数运算规则的理解和运用。也就是说, 学习这种数学解释法设计的代数运算样例, 足以使一些初学代数运算的六年级小学生理解新算符和代数运算规则的数学含义。当然, 为了兼顾学生数学学习能力的个体差异, 在教学实践中教师可以先让学生学习数学解释的样例, 然后再学习文字解释的样例。这样的结合既可以培养学生对数学语言的理解能力和抽象逻辑思维能力, 又可以使学生准确地理解新算符和新规则的定义概念和运算规则, 同时兼顾了学生数学学习能力的个体差异。值得一提的是, 学生用母语学习了数学概念和运算规则的数学意义后, 学生还要在实际运算中运用数学语言。所以, 这种“数学解释”具有培养学生直接运用数学语言理解数学概念和运算规则的功能。

实验1与以前的同类研究(林洪新, 张奇, 2007)相比, 被试都是六年级小学生, 学习的运算规则也都相同(即都是“完全平方和”和“平方差”运算规则),但学习效果却明显优于以前研究的学习效果。比较前后两种实验研究, 所不同的只是运算样例的设计不同。在以前的实验中, 让被试学习的是没有数学解释的“完整”样例和“不完整”样例, 尽管在不完整的样例学习中运用了“有反馈”和“无反馈”的方法,可是实验结果却表明, 除了少数被试外, 大多数被试很难学会两种代数运算规则。其原因已经在前文谈过, 主要原因就是在样例中缺少对新算符和新运算规则的数学解释。这表明采用“解释法”设计代数运算样例有效地解决了以前研究中, 六年级小学生难以用完整和不完整样例学会代数运算规则的难题。

“数学解释法”样例设计的提出, 不仅成功地解决了小学生运用数学运算样例学习“完全平方和”和“平方差”两种代数运算规则的问题, 而且预示着学生通过采用“解释法”设计的其它代数运算样例的学习, 还可以学会其他含有新算符的代数运算规则。因为在数学中几乎所有的新算符都可以用已知的算符来解释。前文列举过的例子无需赘述, 没有列举的也是不胜枚举。例如, 如果小学生学过了乘法运算, 那他们就可以通过“a=a, a × a=a, a × a ×a=a”等运算样例的学习, 学会乘方运算规则以及“n个a相乘等于a”的一般数学原理。再如, 如果小学生学过了乘法运算, 他们就可以通过“1!=1, 2!=1 × 2, 3!=1 × 2 × 3”等运算样例的学习, 学会阶乘运算规则, 并领悟阶乘“n!=1 × 2 × 3…(n – 1)n”的一般公式。又如, 如果被试具有了三角形的几何知识和比例运算知识, 就可以运用“sinα=a/c, cosα=b/c, tanα=a/b”等样例的学习, 理解三角函数的运算含义等等。正是因为数学运算规则和运算符号之间普遍存在着这种严密的逻辑关系, 所以, 在数学运算样例中, 几乎所有的新算符都可以用学生已知的算符来解释。这就为数学运算规则的样例学习提供了普遍的可能性或可行性。除了“解释法”的运用之外, 还可以运用下面要讨论的“解释−标记法”和“转换标记法”。

3.2 “解释−标记法”样例设计对代数运算规则样例学习效果的影响

已有大量研究证明, 在运算样例中适当地添加运算标记对样例学习有促进作用(邢强, 莫雷, 2002;张华等, 2013; 张奇等, 2014)。而且, Sturz, Brown和Kelly (2009)研究也表明视觉标记有助于空间关系的习得。Amadieu, Mariné和Laimay (2011)的研究证实了“线索”能降低动画学习过程中的认知负荷, 提高对高成分互动性材料的理解。

当然, “标记法”的运用也要适当, 只有运用得当才能发挥其作用。因为, 张奇和林洪新(2005)研究表明, 运算步骤标记对学习较难的“无括号”运算规则的促进作用明显, 但对学习较简单的“小括号”运算规则的促进作用不明显。同理, “解释−标记法”的运用也要适当, 适当运用就会起积极的促进作用,例如, 在张奇等人(2014)的研究中“解释−标记法”就起到了比“解释法”起到了更好的促进作用。可是,如果运用不当, 也会起消极的妨碍作用。

实验2就采用“解释−标记法”设计了“完全平方和”和“平方差”的运算样例, 并与“解释法”样例的学习迁移效果进行比较。原来的设想是“解释−标记法”样例的学习效果应该比“解释法”样例的学习效果更好。可是实验结果却表明, “解释−标记法”样例只在“平方差”运算样例学习的近迁移测验成绩上明显优于“解释法”样例, 但在远迁移成绩上差异不明显。而且, 学习采用“解释−标记法”设计的“完全平方和”运算样例的远、近迁移测验成绩均不明显好于“解释法”样例的学习迁移成绩。究其原因, 可能是由于实验2中的“解释−标记法”运用不当造成的。因为, 在以前的研究(张奇等, 2014)中, “解释−标记法”的运用只是对样例中起“解释”作用的内容加上了红色标记, 而且没有虚线和箭头等转换标记。可是在实验2的“解释−标记法”样例设计中没有给“解释”的内容加上了红色标记, 而是在运算样例的前后运算步骤之间加上了用红色虚线和箭头组成的运算步骤转换标记。这种方法实际上就是“解释法”与“转换标记法”的结合运用, 应该称为“解释−转换标记法”。采用这种方法设计的运算样例是在“解释法”样例中添加了许多指明运算步骤之间前后对应关系的红色箭头标记。这些转换标记的增加一方面可能会促进被试对前后运算步骤之间关系的理解。但由于这些标记过多地充斥于运算样例中, 使被试看起来有眼花缭乱的感觉。也就是说, 这些过多的“箭头标记”额外地消耗了被试有限的认知资源, 对样例学习反而起了妨碍作用, 从而降低了标记作用的发挥。所以, 使得学习“解释−标记法”样例的远、近迁移成绩只是略好于学习“解释法”样例的迁移成绩, 而没有达到全部显著好于“解释法”样例。至于为什么“解释−标记法”样例设计只在“平方差”运算样例学习的近迁移测验成绩上明显优于“解释法”样例, 还需要进一步的分析和探究。

3.3 “整体呈现”和“分步呈现”对代数运算规则学习迁移效果的影响

已有研究表明, 样例的呈现方式影响其学习效果。例如, Renkl和Athinson (2003)验证了以“渐减程序” (fading procedure)的方式呈现样例对学习效果的促进作用。渐减程序即首先呈现完整的样例,然后逐步省略解题步骤, 最后仅剩下待解决的问题。Clark等人(2005)在双内容样例学习的研究中发现, 在新手的学习效果上, 相继呈现“双内容”样例好于同时呈现两者。Spanjers等人(2011)在动态样例学习的研究中, 将样例分段呈现, 即将较长的动态样例分成几个段落呈现。实验结果证明, 分段呈现动态样例的学习效果较好。上述实验结果表明,不论是逐步渐减呈现不完整样例, 还是相继呈现双内容样例和分段呈现动态样例, 其实质都是每次呈现较少的样例内容, 这样可以降低每次学习的认知负荷, 从而提高样例的整体学习效果。在认真分析了实验2运用“解释−标记法”不当的基础上, 实验3运用了分步呈现 “解释−标记法”样例的方式, 并与整体呈现样例的学习效果进行了对比实验研究。实验结果表明, 在“完全平方和”和“平方差”两种代数运算样例的学习迁移成绩上, 学习分步呈现样例的远、近迁移成绩均显著优于学习整体呈现样例的迁移成绩。其原因主要有三：首先, 在分步呈现的“解释−标记”样例中, 由于每次呈现的运算步骤和标记较少, 被试每次学习都能够清晰地看清前后运算步骤之间的对应关系, 避免了样例整体呈现时因标记过多所导致的眼花缭乱的感觉。其次, 分步呈现样例时, 学生每次学习较少的步骤, 降低了每次学习的认知负荷。最后, 由于被试在实验过程中可以通过点击“下一步”或“上一步”按钮来自主控制每步的学习时间, 并保持与前后步骤的衔接, 保持了样例学习的完整性, 从而提高了样例的整体学习效果。所以, 对于运算步骤较多和“转换标记”过多的样例,采用被试自主控制的“分步呈现”样例的分段学习方式, 其学习效果显著优于整体呈现样例的学习效果。

4 结论

(1)六年级小学生学习采用“解释法”设计的“完全平方和”和“平方差”代数运算样例, 其学习迁移成绩明显优于学习普通样例的迁移成绩。

(2)在“解释法”设计的样例上添加“运算标记”要运用适当, 如果运用不当, 特别是“运算标记”过多时, 容易增加样例学习的认知负荷, 从而降低标记的使用效果。

(3)对于运算步骤较多和“运算标记”过多的样例, 采用被试自主控制的“分步呈现”样例的学习方式, 其学习效果显著优于整体呈现样例的学习效果。

Adams, D. M., McLaren, B. M., Durkin, K., Mayer, R. E.,Rittle-Johnson, B., Isotani, S., & van Velsen, M. (2014). Using erroneous examples to improve mathematics learning with a web-based tutoring system.

Computers in Human Behavior, 36

,401–411.Amadieu, F., Mariné, C., & Laimay, C. (2011). The attention-guiding effect and cognitive load in the comprehension of animations.

Computers in Human Behavior, 27

(1), 36–40.Anderson, J. R., & Fincham, J. M. (1994). Acquisition of procedural skills from examples.

Journal of Experimental Psychology: Learning,Memory and Cognition, 20

(6), 1322–1340.Bokosmaty, S., Sweller, J., & Kalyuga, S. (2015). Learning geometry problem solving by studying worked examples:Effects of learner guidance and expertise.

American Educational Research Journal, 52

(2), 307–333.Bourne, L. E., Goldstein, S., & Link, W. E. (1964). Concept learning as a function of availability of previously presented information.

Journal of Experimental Psychology, 67

(5),439–448.Carroll, J. S., Galegher, J., & Wiener, R. (1982). Dimensional and categorical attributations in expert parole decisions.

Basic and Applied Social Psychology, 3

(3), 187–201.Chase, W. G., & Simon, H. A. (1973). Perception in chess.

Cognitive Psychology, 4

(1), 55–81.Clarke, T., Ayres, P., & Sweller, J. (2005). The impact of sequencing and prior knowledge on learning mathematics through spreadsheet applications.

Educational Technology Research and Development, 53

(3), 15–24.Koedinger, K. R., & Aleven, V. (2007). Exploring the assistance dilemma in experiments with cognitive tutors.

Educational Psychology Review, 19

(3), 239–264.Lee, C. Y., & Chen, M. J. (2015). Effects of worked examples using manipulatives on fifth graders' learning performance and attitude toward Mathematics.

Journal of Educational Technology & Society, 18

(1), 264–275.Lin, H. X., & Zhang, Q. (2007). Effects of worked example learning on learning algebraic operations.

Acta Psychologica Sinica, 39

(2), 257–266.[林洪新, 张奇. (2007). 小学生代数运算规则的样例学习.

心理学报, 39

(2), 257–266.]Renkl, A., & Atkinson, R. K. (2003). Structuring the transition from example study to problem solving in cognitive skill acquisition: A cognitive load perspective.

Educational Psychologist, 38

(1), 15–22.Renkl, A., Atkinson, R. K., Maier, U. H., & Staley, R. (2002).From example study to problem solving: Smooth transitions help learning.

The Journal of Experimental Education,70

(4), 293–315.Renkl, A., Hibert, T., & Schworm, S. (2009). Example-based learning in heuristic domains: A cognitive load theory account.

Educational Psychology Review, 21

(1), 67–78.Richey, J. E., & Nokes-Malach, T. J. (2013). How much is too much? Learning and motivation effects of adding instructional explanations to worked examples.

Learning and Instruction,25

, 104–124.Schworm, S., & Renkl, A. (2006). Computer-supported examplebased learning: When instructional explanations reduce self-explanations.

Computer & Education, 46

(4), 426–445.Seufert, T. (2003). Supporting coherence formation in learning from multiple representations.

Learning and Instruction,13

(2), 227–237.Spanjers, I. A. E., Wouters, P., van Gog, T., & van Merriënboer,J. J. G. (2011). An expertise reversal effect of segmentation in learning from animated worked-out examples.

Computers in Human Behavior, 27

(1), 46–52.Sturz, B. R., Brown, M. F., & Kelly, D. M. (2009). Facilitation of learning spatial relations among locations by visual cues:Implications for theoretical accounts of spatial learning.

Psychonomic Bulletin & Review, 16

(2), 306–312.Sweller, J., & Cooper, G, A. (1985). The use of worked examples as a substitute for problem solving in learning algebra.

Cognition and Instruction, 2

(1), 59–89.van Gog, T., Paas, F., & van Merriënboer, J. J. G. (2008).Effects of studying sequences of process-oriented and product-oriented worked examples on troubleshooting transfer efficiency.

Learning and Instruction, 18

(3), 211–222.Wittwer, J., & Renkl, A. (2010). How effective are instructional explanations in example-based learning? A meta-analytic review.

Educational Psychology Review, 22

(4), 393–409.Wynder, M. B., & Luckett, P. F. (1999). The effects of understanding rules and a worked example on the acquisition of procedural knowledge and task performance.

Accounting& Finance, 39

(2), 177–203.Xing, Q., & Mo, L. (2002). Effects of subgoal encoding of examples on the use of principle in new problem solving.

Psychological Development and Education, 19

(1), 55–59.[邢强, 莫雷. (2002). 样例的子目标编码对新问题解决中原理运用的作用研究.

心理发展与教育, 19

(1), 55–59.]Xu, D. Z., & Zhang, Q. (2011). The effect of learning the hydrocarbon covalent bond structural formula by correct and incorrect combined worked-examples.

Journal of Psychological Science, 34

(2), 386–392

.

[许德志, 张奇. (2011). 碳氢共价键结构式正误样例组合的学习效果.

心理科学, 34

(2), 386–392.]Zhang, H., Qu, K. J., & Zhang, Q. (2013). The effective design of worked-example for learning algebra operation rules containing new operators.

Acta Psychologica Sinica, 45

(10),1104–1110.[张华, 曲可佳, 张奇. (2013). 含有新算符的代数运算规则学习的有效样例设计.

心理学报, 45

(10), 1104–1110.]Zhang, Q., & Cai, C. (2015). Worked-examples learning of the rules: Experiment study and theoretical exploration.

Studies of Psychology and Behavior, 13

(5), 614–620.[张奇, 蔡晨. (2015). 规则样例学习的实验研究和理论探索.

心理与行为研究, 13

(5), 614–620.]Zhang, Q., & Guo, F. F. (2008). Schoolpupils' learning of the operation rules of removing brackets.

Psychological Science,31

(1), 70–74.[张奇, 郭菲菲. (2008). 小学生“去括号”运算规则的样例学习.

心理科学, 31

(1), 70–74.]Zhang, Q., & Lin, H. X. (2005). Worked example learning about the rules of the four fundamental admixture operations of arithmetic

. Acta Psychologica Sinica, 37

(6), 784–790.[张奇, 林洪新. (2005). 四则混合运算规则的样例学习.

心理学报, 37

(6), 784–790.]Zhang, Q., & Zhang, H. (2014). The effect of learning objects force analysis by correct and incorrect combined worked examples.

Journal of Psychological Science, 37

(1), 117–123.[张奇, 张华. (2014). 物体受力分析正误样例组合的学习效果.

心理科学, 37

(1), 117–123.]Zhang, Q., Zheng, W., & Wan, Y. (2014). A positive impact of worked examples designed by “the method of explained”on pupils’ learning new operational rules.

Psychological Development and Education, 30

(2), 153–159.[张奇, 郑伟, 万莹. (2014). “解释法”样例对小学生学习新运算规则的促进.

心理发展与教育, 30

(2), 153–159.]