缺失数据的结构方程建模：全息极大似然估计时辅助变量的作用*

王孟成 邓俏文

(广州大学心理系; 广州大学心理测量与潜变量建模研究中心, 广州 510006)

1 引言

在对心理学等社科调查的数据进行建模时, 常常遇到数据缺失的情况。例如, 研究参与者拒绝接受调查、不愿意回答或遗漏某些问题。毫不夸张的说, 数据缺失无法避免, 因此如何处理缺失数据就成了摆在研究者面前重要而又无法回避的问题。

全息极大似然估计(Full Information Maximum Likelihood, FIML)和多重插补(Multiple Imputation,MI)是目前缺失数据建模最为学者推崇的方法(Graham, 2009; Schafer & Graham, 2002)。这两种方法在特定条件下所得结果是等价的, 但鉴于建模软件的可获得性、统计处理的便捷性以及结果的稳健性(e.g., Yuan, Yang-Wallentin, & Bentler, 2012), 在方法学实践中FIML更加方便和灵活(Yuan et al.,2012; 王孟成, 叶浩生, 2014)。

在缺失数据建模实践中, 方法学者通常会建议纳入辅助变量(auxiliary variable)来提高结果的稳健性。采用FIML处理缺失数据时, 合理利用辅助变量可以使与FIML密切相关的缺失机制得到满足,从而产生更可靠的参数估计, 增加统计功效(Collins,Schafer, & Kam, 2001; Graham, 2009)。然而, 当前方法学领域对纳入辅助变量的研究还有些重要的问题尚未探明。例如, 纳入自身就存在缺失的辅助变量是否有益？因此, 本研究拟采用蒙特卡洛模拟的方法对尚存的问题做进一步的探索, 希望为应用研究者合理使用辅助变量提供有益的指引。

1.1 数据的缺失机制与现代的处理方法

美国统计学家Rubin (1976)最早将缺失机制分为3类：完全随机缺失、随机缺失和非随机缺失。完全随机缺失(Missing Completely at Random,MCAR)指变量缺失发生的可能性与变量自身及其他变量都无关, 即变量出现缺失这一事件是随机事件。随机缺失(Missing at Random, MAR)指变量缺失发生的可能性与模型中某些观测变量有关而与该变量自身无关, 即缺失发生的可能性与其他变量有关。非随机缺失(Missing Not at Random, MNAR)指变量缺失发生的可能性只与自身相关。

现代处理缺失数据的方法中, 最为研究者推崇的是全息极大似然估计和多重插补(Enders &Bandalos, 2001; Graham, 2009; Schafer & Graham,2002)。随着统计软件的发展, 这两种方法得到了广泛的应用(e.g., Kidger et al., 2015)。

在处理缺失数据时, FIML使用所有观测变量的全部信息进行参数估计, 因而又称为全息极大似然估计。在满足MCAR和MAR的条件下, FIML产生无偏和有效的参数估计。FIML处理缺失值并没有使用替代值对缺失值进行替换, 而是根据未缺失数据的信息采用迭代的方式进行估计(Enders &Bandalos, 2001; Graham, 2009)。

MI假设在数据随机缺失情况下, 用两个或更多能反映数据本身概率分布的值来插补缺失数据。一个完整的MI包含3步：数据插补, 计算和汇总。理论上, 在插补次数无限的情况下, MI与FIML结果一致。

两种方法都是目前处理缺失数据最有效的方法, 但两种方法又有着显著的不同。首先, FIML是专门用于模型分析的参数估计方法, 严格意义上来说, MI是基于统计模型的处理过程。其次, FIML分析时并非填补缺失值, 而是根据已知信息采用迭代的方式进行估计, MI需要填补数据再进行后续分析。最后, 运用MI处理缺失数据时辅助变量的效用还没有一致的结论, 尤其是在实际数据处理中(Mustillo, 2012)。基于以上FIML和MI特点的比较,以及本文主要研究与辅助变量相关的内容, 本研究只关注FIML处理缺失数据时辅助变量的相关问题。

1.2 辅助变量

辅助变量是研究者不感兴趣, 但能为缺失数据建模提供有用信息的变量(Enders, 2008)。提供辅助信息的变量通常是造成数据缺失的原因变量或者与研究变量相关的变量。

由于MAR机制包含了未观测的数据, 因此在缺少这些未观测数据的条件下, 无法在统计上对数据是否满足MAR进行检验(Raykov, 2011)。为了克服这一不足, 方法学者提出使用纳入辅助变量的方式来提高满足MAR假设的可能性(Collins et al.,2001; Schafer & Graham, 2002; Yuan & Lu, 2008)。目前在FIML分析中, 最常用的纳入辅助变量的方式是通过Graham (2003)提出的饱和关联模型(saturated correlates model, SCM)。在SCM中, 通常允许辅助变量间、辅助变量与外生观测指标以及内生观测指标的测量误差相关。在SCM提出之前, 运用ML处理缺失数据比较麻烦, 因此先前的研究多侧重通过专门运用MI的软件包NORM (Schafer,1999)进行缺失数据处理。采用MI处理缺失数据时,纳入辅助变量很方便, 但由于插补次数所导致结果的不确定性, 人们开始寻找ML下如何处理缺失数据的方法(Graham, 2003)。采用FIML进行分析时,若要纳入辅助变量, 某些潜变量建模软件(如Mplus)会默认采用SCM (Muthén & Muthén, 1998-2010)。SCM的提出为FIML/SEM处理缺失数据提供了很大的便利, 也使得Mplus等自动采用SCM模型的软件成为运用FIML/SEM处理实际缺失数据或模拟研究常用的软件(Enders, 2008; 王孟成, 2014)。

2 问题提出

2.1 先前类似研究

先前的模拟研究多数只考虑了辅助变量不缺失的情况(Collins et al., 2001; Graham, 2003;Mustillo, 2012)。例如, Graham (2003)的研究通过SCM对单个不缺失的辅助变量进行FIML/SEM分析。这些模拟研究均发现不缺失的辅助变量与研究变量高度相关时, 纳入辅助变量能够改善模型参数估计。Mustillo (2012)的研究在回归模型中通过MI处理缺失值, 探究辅助变量类型、研究变量的缺失率与缺失机制的关系, 该研究发现纳入辅助变量对参数估计没有明显的改善。然而Collins等(2001)指出, 即使纳入与缺失变量无关的辅助变量, 得到最坏的结果也是中性的, 并不会恶化参数估计。而当与缺失变量相关的辅助变量被忽略时, 均值、方差、回归估计会产生实质性的偏差。

另外, 纳入辅助变量进行缺失数据分析时, 不仅研究变量存在缺失, 辅助变量也常常存在缺失。当辅助变量也存在缺失时, 情况又会如何？为数不多的研究表明, 尽管纳入有缺失的辅助变量不如纳入完全的辅助变量那么有效, 但纳入总比忽略它更有益(Enders, 2008; Hardt, Herke, & Leonhart, 2012;Yoo, 2009)。例如, Enders (2008)采用FIML/SEM对研究变量的缺失机制(MAR)、单辅助变量的缺失机制(MCAR, MNAR)、辅助变量的缺失率(25%、50%)、相关程度(

r

=0.54,

r

=0.90)进行考查, 结果发现即使辅助变量缺失50% (且辅助变量的缺失机制为MNAR), 纳入它也有利于参数估计。虽然以上研究考虑到辅助变量有缺失的情况, 但它们主要研究辅助变量与研究变量各自的缺失率或设定辅助变量的缺失率后, 让研究变量的缺失率依辅助变量的缺失率而定(Enders, 2008), 而两变量各自的缺失并不等于研究样本中两变量共同的缺失(简称共缺)。

共缺指同一个体的数据在研究变量上有缺失,在辅助变量上也有缺失, 共缺率则是共缺频数在样本中的比例。因此, 研究变量与辅助变量共缺时,参数估计的情况成了数据分析时的另一个问题。Von Hippel (2007)指出, 即使辅助变量与研究变量呈高相关, 当辅助变量与研究变量共缺时, 结果也得不到改善。Enders (2008)的研究无意中发现当辅助变量与研究变量的共缺率达到15%时, 结果会产生明显的偏差。但这个问题目前并没有得到系统研究。因此更多的缺失机制组合、共缺率、辅助变量数等问题需要作进一步的探讨。

2.2 本研究的目的

通过文献回顾不难发现, 至少还有如下4个问题亟待解决：第一, 先前研究只探讨了单个辅助变量的情况。当有多个辅助变量且样本量足够大的时候, 以上问题会发生怎样的变化？第二, 上述研究并没有对无意中发现的共缺率问题做进一步的探索; 第三, 以往研究仅局限在MAR机制的研究变量与MCAR和MNAR的辅助变量, 没有进一步探究研究变量与辅助变量其他的缺失机制组合(简称共缺机制); 第四, 先前的研究在参数设定时参考Collins等(2001)的模型, 该研究设定辅助变量与研究变量的相关程度过高(0.54, 0.90), 这在实际研究中并不多见。

针对以上4点, 本研究通过蒙特卡洛模拟, 采用FIML处理结构方程建模中的缺失数据, 主要目的是探究辅助变量与研究变量的共缺机制、共缺率、相关程度、辅助变量数与样本量这些因素对参数估计结果的影响。

3 研究设计

3.1 模拟研究设计

3.1.1 研究假设模型

本研究设定的模型参照Enders (2008)的研究,模型由两个因子(X和Y)构成结构模型, 每个因子有3个观测指标, 外生潜变量X对内生潜变量Y的回归系数设为0.60。外生潜变量X的指标(x1, x2和x3)的数据不缺失, 内生潜变量Y的指标(y1, y2和y3)的数据存在缺失, 辅助变量Z是一个/组有缺失的观测变量(具体见下一小节)。

Collins等(2001)的研究发现, 辅助变量与研究变量之间的相关系数最好能达到0.4以上, 在他们的研究中, 研究变量间还设定

ρ

=0.90的高度相关, 然而在实际研究中如此高的相关并不多见。因此, 在参考前人研究(Enders & Peugh, 2004; Hardt et al., 2012)的基础上, 本研究考虑如下两组相关水平：低相关设为

ρ

=0.2,

ρ

=0.3和中等偏高相关为

ρ

=0.5,

ρ

=0.6。所有变量服从标准正态分布,即均值为0, 方差为1, 固定因子方差为1, 因子负荷为0.70, 残差方差为0.51。存在多个辅助变量时,综合Hardt等(2012,

r

=0.1或

r

=0.5)与Enders和Peugh (2004,

r

=0.3)的研究, 本研究设定辅助变量之间的相关系数为0.4。

参照Graham (2003)提出的饱和关联模型, 图1给出了单个辅助变量的饱和关联模型(辅助变量与研究变量呈低/高相关)。

3.1.2 缺失机制

当研究变量的缺失机制为MNAR时, 即变量缺失发生的可能性只与自身相关时, 纳入辅助变量无法改善参数估计结果(Enders, 2006; Yoo, 2009)。再者, 当研究变量与辅助变量的共缺率很大, 缺失机制都是MNAR时, 此时任何方法都难以得到无偏的估计结果, 因此本研究只考虑研究变量Y的2种缺失机制(MAR & MCAR)与辅助变量Z的3种缺失机制(MAR, MCAR, & MNAR), 共6种共缺机制组合。

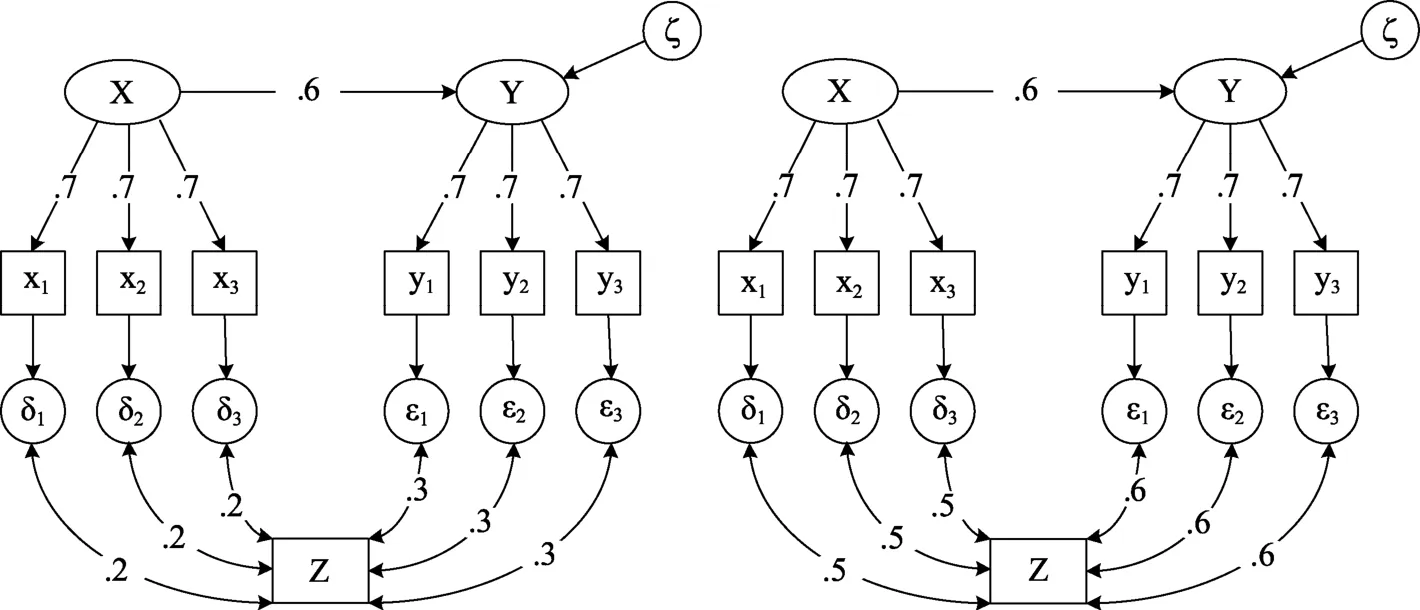
图1 蒙特卡洛模拟所依据的模型路径图

与先前类似研究一致(Enders, 2008), 本研究采用逻辑回归生成缺失数据。具体来说, 当Y观测变量的缺失机制为MAR时, 设定Y的缺失与辅助变量Z有关, 斜率参数为正, 即Z的值越大, Y的缺失率越大。当辅助变量Z的缺失机制为MAR时, 设定Z的缺失与X观测变量有关, 斜率参数设为负,即X观测变量的值越大, Z的缺失率越小。当辅助变量Z的缺失机制为MNAR时, Z的缺失与自身相关, 设定斜率参数为负, 即Z的值越大, Z的数据缺失率越小。这样, 当共缺组合形式为MAR-MNAR时, 辅助变量可为研究变量提供更多的信息, 同时可减少研究变量与辅助变量的缺失都是由辅助变量的缺失造成的可能性。

3.1.3 样本量和缺失率

表1汇总了先前相关模拟研究中, 样本量和缺失率的设置数据。大多数研究设置的样本量在200～500之间, 考虑到大多数心理学调查研究和FIML对样本量的要求, 本研究的样本量设为100、200、500和1000。表中设定的缺失率指单纯研究变量的缺失率或辅助变量的缺失率。根据Enders(2008)的研究, 当研究变量与单辅助变量的共缺率达到8%时, 辅助变量的纳入能使结果得到改善,所得参数估计结果偏差很小, 而当共缺率达到15%时, 参数估计偏差显著增加。因此本研究设定辅助变量与研究变量的共缺率为5%、10%、15%和20%。

表1 相关模拟研究设置的样本量与缺失率参数汇总

3.1.4 辅助变量数

不少研究建议纳入辅助变量进行缺失数据分析, 但对于纳入多少个辅助变量的问题在以往的研究中并没有专门探讨。Enders (2008)主要研究一个辅助变量的情况, 本研究的模拟方法参考Enders(2008)基于FIML/SEM的研究, 并与该研究结果进行比较。另外, 综合模拟设置的最小样本量、最大缺失率及结构方程模型的要求, 本研究主要考察1个、3个和5个辅助变量的情况。

3.1.5 数据生成

本研究所有的数据生成与分析均采用Mplus 7.0 (Muthén & Muthén, 1998-2010)完成。本研究共模拟3种情况：(1) 研究变量缺失, 辅助变量不缺失, 且在建模时纳入辅助变量; (2) 研究变量和辅助变量共缺, 且在建模时纳入辅助变量; (3) 研究变量与辅助变量共缺, 但在建模时不纳入辅助变量。第一种模拟条件由第二种模拟条件设定辅助变量不缺失得到, 其中的缺失机制组合形式实质上只是研究变量的缺失机制, 但这两种条件下研究变量的缺失率相同。第三种模拟条件由第二种模拟条件在模型分析时, 不纳入辅助变量进行分析而得到。

每种模拟共有576种组合, 每种组合均重复5000次。后两种模拟条件中控制的因素有：4种样本量(100、200、500、1000)、4种共缺率(0.05、0.10、0.15、0.20)、6种共缺机制组合(MAR-MAR, MARMCAR, MAR-MNAR, MCAR-MAR, MCAR- MCAR,MCAR-MNAR)、3种辅助变量数目(1、3、5)、两种相关程度(低相关

ρ

=0.2,

ρ

=0.3和中等偏高相关

ρ

=0.5,

ρ

=0.6)。

3.2 结果评价标准

采用模拟研究中常用的两个评估标准：参数估计的偏差(e.g., Enders & Bandalos, 2001; Yoo, 2009)和覆盖率(Coverage; Yoo, 2009)。

比较常用的估计偏差的指标是标准偏差(Standardized Bias; Collins et al., 2001; Enders &Gottschall, 2011), 标准偏差=(平均估计值−理论值)/平均标准误(以示区分, 记为偏差)。如果偏差等于–0.5, 意味着该平均估计值处于理论值–0.5个标准误的位置。Collins等(2001)指出偏差小于0.4为无偏估计, 后来的研究也采用此标准(Enders& Gottschall, 2011)。但有研究质疑以0.4作为判断标准的适切性(Graham, 2009), 因此当偏差出现的情况较多时, 本研究同时采用偏差(Bias)作为结果评价指标。

蒙特卡洛模拟中, 偏差可通过以下公式得到：

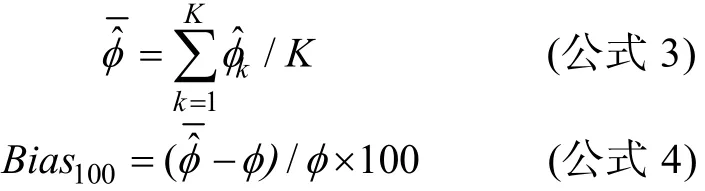
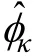
另外, 在模拟研究中, 覆盖率表示每次重复模拟计算所得结果等于/接近真值的比例, 类似于参数区间估计(频率论)的置信区间：区间包含的真值。但这里的置信区间所允许的犯错误的概率(即显著性水平)不是固定的, 显著性水平=1−覆盖率。所以,当覆盖率为0.95时, 意味着在抽样1000次(模拟计算)得到的结果所组成的区间中, 有950次得到的估计值在总的区间中包含了真值, 此时犯错误的概率为0.05。前人的研究认为覆盖率小于0.90是不可接受的(Collins et al., 2001; Enders & Peugh, 2004),本研究也采用0.90的标准。

4 结果

综合前人研究考虑的需要模型估计的参数(Collins et al., 2001; Enders, 2008), 本研究主要考虑因子负荷和回归系数的估计值。其中因子负荷的结果(偏差与覆盖率)由对应结果求平均数得到(即条目因子负荷之和除以条目个数)。由于版面限制本研究只呈现了部分结果(

n

=500), 更多的结果(其他样本量与偏差的结果)可与作者联系获得。

4.1 辅助变量不缺失

建模时纳入不缺失的辅助变量, 估计结果的偏差和覆盖率都在可接受范围。总的来说, 样本量越大, 因子负荷和回归系数的偏差值越小。对于小样本(

n

=100), 辅助变量越多, 回归系数的偏差越大。对于回归系数的参数估计而言, 随着样本量的增大,纳入单个辅助变量依然是有益的。另外, 辅助变量越多(

n

=100除外), X因子负荷的偏差越小。在此模拟的各种条件下, 覆盖率均达标且变化不大。

4.2 辅助与研究变量共缺：建模时纳入辅助变量

在此条件下, 只有回归系数的参数估计产生偏差, 其他参数均无偏。对于回归系数的结果,“MCAR-”组合形式的参数估计结果都无偏。偏差多出现在“MAR-”组合形式中, 且样本量越大, 出现偏差的情况越多。相关越高, 越容易出现偏差。

在此模拟条件下, X、Y因子负荷的覆盖率都在可接受范围内。在高相关、MAR-MAR组合条件下,纳入5个辅助变量时, X因子负荷的覆盖率比其他辅助变量数目条件下的稍高(差异在0.01～0.02之间), 然而Y因子负荷没有呈现此特点。同样条件下, 回归系数的覆盖率更容易出现不可接受的结果(低相关条件下的结果几乎全无偏), 有偏的结果全部出现在“MAR-”组合上(

n

=100无偏)。与Enders(2008)结果一致的是, 当

n

=500且研究变量的缺失机制为MAR时, MAR-MCAR组合似乎比MARMNAR组合出现偏差的情况更多(见表2)。而且在MAR-MCAR组合上, 当共缺率达到15%时, 单辅助变量的情况下出现明显的偏差, 这也是为什么Enders (2008)的研究发现影响参数估计结果的因素主要是辅助与研究变量的共同缺失模式(共缺率),而不是缺失机制。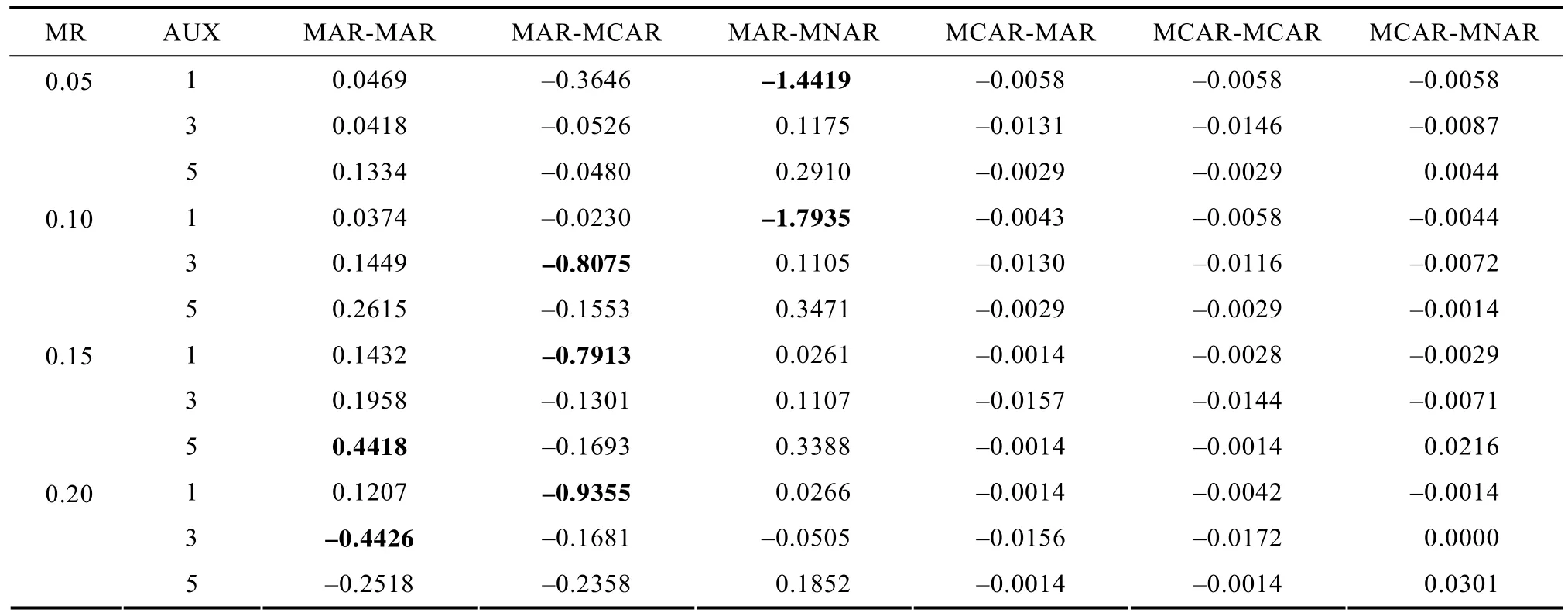

表2 辅助变量与研究变量共缺且纳入辅助变量时回归系数的估计偏差S.E(n=500, 中等偏高相关)

4.3 辅助与研究变量共缺：建模时不纳入辅助变量

在此模拟条件下, 大多数共缺机制组合下的结果都出现严重的偏差, 且高相关或辅助变量数多的条件下更容易出现偏差, 偏差与覆盖率的结果呈现一致的规律。但是Y因子负荷的偏差都在接受范围内, 且随着样本量的增大, 可接受的偏差值减小。另外, 即使是MCAR的研究变量, 估计结果也会出现偏差。与前一种模拟情况类似, 偏差多出现在“-MAR”、“-MCAR”组合上, “-MNAR”组合较少出现偏差(见表3)。

4.4 不同模拟条件间的比较

由于第一种模拟条件由第二种模拟条件设定辅助变量不缺失得到, 即两种条件下的研究变量的缺失率、缺失机制等是相同的, 通过比较这两种模拟条件下的结果发现, 辅助变量有缺失比不缺失时产生严重偏差的可能性更大。

相对于第二种模拟的条件, 在第三种模拟条件下, 偏差主要出现在X因子负荷和回归系数上。通过相关程度、辅助变量数、样本量的比较, 发现偏差主要出现在中等偏高相关条件下; 且辅助变量越多, 出现偏差的情况越多; 样本量越大, 出现偏差的情况也越多。通过比较高相关条件下X因子负荷偏差的结果, 发现在不纳入辅助变量的条件下,MAR-MCAR, MCAR-MAR和MCAR-MCAR这3种组合的结果都出现偏差。纳入辅助变量之后, 结果得到明显的改善, 尤其是“MCAR-”组合, 估计结果的偏差全部都在可接受范围内。

通过比较第二种模拟和第三种模拟回归系数的结果(见表4), 发现在不纳入辅助变量时, 所有缺失机制的组合结果都出现偏差。其中, 在“MAR-”组合形式的MAR-MAR出现偏差数量最少; 在“MCAR-”组合形式中的MCAR-MNAR出现偏差数量最少。随着样本量的增大, 出现偏差的数量增多。纳入辅助变量之后, “MCAR-”组合结果全部在可接受范围内。“MAR-”组合的结果在小样本的条件下无偏, 大样本时依然出现偏差, 但有偏的结果得到明显的改善。纳入辅助变量之后, 即使辅助变量与研究变量呈低相关, 因子负荷和回归系数的估计同样得到了改善, 可接受的偏差值变小。

5 讨论与结论

Enders (2008)的研究主要考虑辅助变量的缺失率、缺失机制对参数估计的影响。本研究在Enders(2008)的基础上, 进一步考查辅助变量与研究变量的共缺率、共缺机制、相关程度、辅助变量数目及样本量对参数估计结果的影响。

5.1 缺失机制的影响

当辅助变量与研究变量共缺时, 相对于MNAR的辅助变量, MCAR的辅助变量更容易出现参数估计偏差。这说明, 即使辅助变量的缺失机制为MNAR, 纳入模型进行分析也有利于改善参数估计(Enders, 2008)。Enders (2008)指出由于MCAR辅助变量的无方向性或不确定性, 增大了辅助变量的缺失机制与研究变量的缺失机制是由共同因素造成的可能性, 而MNAR辅助变量与研究变量的缺失机制能够重合的机会较少。所以当辅助与研究变量共缺时, 如果采用纳入辅助变量的方法进行缺失数据分析, 不能因为辅助变量的缺失机制为MNAR而有过多的顾虑, 因为共缺组合机制为MARMNAR或MCAR-MNAR所得到的结果比MARMCAR或MCAR-MCAR要好。另外, 尽管MAR与MCAR都是可忽略缺失, 但MCAR的假设更加严格(Rubin, 1976)。因此, 在辅助变量与研究变量呈中等偏高相关, 纳入辅助变量时, 研究变量的缺失机制为MAR较MCAR更容易出现偏差。

表3 辅助变量与研究变量共缺但不纳入辅助变量时X因子负荷的估计偏差S.E(中等偏高相关)

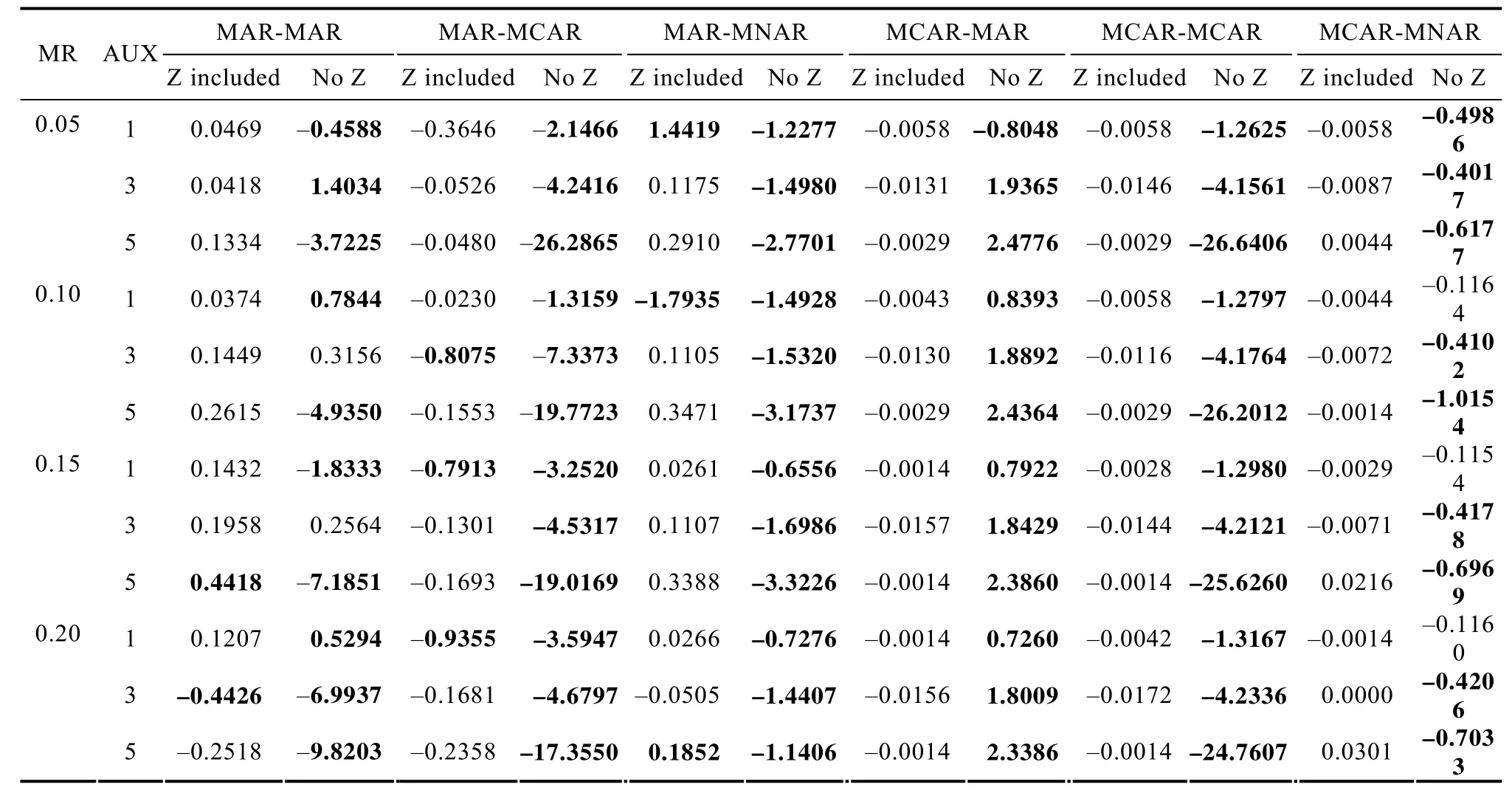
表4 辅助变量与研究变量共缺时纳入与不纳入辅助变量时回归系数的估计偏差S.E比较(n=500, 中等偏高相关)

最后, 需要考虑的一个重要问题是如何判断实际数据的缺失机制是否满足模拟设计下的共缺机制情况, 这涉及到缺失数据机制的检验问题。关于这个问题一直都是这个领域研究的难点, 目前对其的研究也不多(孙婕, 金勇进, 戴明锋, 2013)。尽管我们在本研究中设计了几种缺失值机制的组合, 但是并未涉及如何判断实际研究中如何检验其机制的问题, 我们也没有打算这么做, 因为这个问题超出了本研究的范围。但是, 了解数据缺失的可能原因是必要的, 可以根据经验猜想缺失的可能性, 并通过事后调查或根据已收集到的基本信息进行判断。

5.2 相关程度的影响

本研究发现, 当辅助变量与研究变量的相关只有0.2～0.3时, 纳入辅助变量也有利于得到无偏估计。这一发现与先前的研究结果不同, Hardt等(2012)发现相关太低时(

r

=0.1与

r

=0.5)辅助变量作用不大。Enders和Peugh (2004;

r

=0.1与

r

=0.3)也得到类似的结论。因为辅助变量与研究变量的相关越高,辅助变量能为研究变量提供的信息越多(Collins et al., 2001; Yoo, 2009)。然而, 这可能是由于他们设定的相关太低(

r

=0.1), 导致辅助变量的改善情况不明显。而且, Enders (2008)指出当辅助变量也存在缺失时, 相对于辅助变量与研究变量高相关条件下的估计结果, 中等相关条件下的估计结果更接近于参数或辅助变量完全时的结果。因此, 根据本研究结果,当辅助变量与研究变量的相关达到0.2～0.3时, 即可考虑纳入该辅助变量, 尤其是当共缺组合机制为MAR-MCAR时。

本模拟结果还发现, 在辅助变量不缺失的情况下, 相关程度对研究结果影响不大, 这可能与研究变量的缺失率较低、相关较低有关(Collins et al.,2001)。

5.3 辅助变量的数目

过往的研究发现纳入辅助变量对缺失数据建模是有益的(e.g., Collins et al., 2001; Enders, 2008),本研究也支持这一结论。但是, 很少有研究探讨纳入辅助变量的数目对参数估计的影响, 本研究对此问题做了有益的尝试。本研究发现, 当辅助变量与研究变量存在共缺时, 对于MAR-MAR组合机制,纳入单个辅助变量是有益的; 对于MAR-MCAR或MAR-MNAR组合机制, 纳入多于一个辅助变量的效果更好。

5.4 样本量的影响

在辅助变量不缺失的情况下, 样本量越大, 结果越好。当不纳入辅助变量进行分析时, 样本量越大, 出现偏差的情况越多。另外, 根据Muthén和Muthén (2002)的观点, 在辅助变量对参数估计的影响中, 样本量并非独自起作用, 它还受到变量间的缺失率、缺失机制等因素的影响。结合本研究的结果, 对于回归系数偏差的参数估计(偏差、偏差), 当辅助与研究变量呈低相关, 共缺率为0.20, 辅助变量数为3个的时候, 如果样本量为200或500, 在“MCAR-”组合机制条件下得到的偏差值最大; 而当样本量为1000时, 在“MCAR-”组合机制条件下得到的偏差值最小。控制相关程度、共缺率、辅助变量数不变的情况下, 结果表明“MCAR-”组合机制条件下得到的偏差值随着样本量的增大而减小。对于Y因子负荷偏差的参数估计(偏差、偏差), 相同条件下, 如果样本量为100、500或1000, 在“MCAR-”组合机制条件下得到的偏差值最小。控制相关程度、共缺率、辅助变量数不变的情况下, 结果表明“MCAR-”组合机制条件下得到的偏差值随着样本量的增大而减小。

5.5 共缺率的影响

本模拟结果仅发现纳入不缺失的辅助变量时,相同样本量的情况下, 共缺率越大, Y因子负荷的偏差越大, 其他条件下共缺率的影响并不明显。本研究通过观察所有变量的缺失模式, 计算辅助变量与研究变量共同缺失的比例, 从而得到共缺率。因此, 可能出现如下的情况：辅助变量越多, 每个辅助变量与研究变量的平均共缺率越低, 以至于共缺率对参数估计的影响差别不大。奇怪的是, 在大样本量(

n

=500 或1000)、MAR-MAR组合机制条件下, 随着共缺率的增大, 单个辅助变量时的参数估计的偏差总体呈增大的趋势, 但并非与共缺率同步增大。因此, 缺失数据研究中, 缺失率的影响有待进一步的研究。

5.6 不足与展望

本研究也存在一些不足：第一, 本研究设定的共缺率较低, 这影响了共缺率对辅助变量作用的研究。以后的研究可以考虑模拟更高的共缺率, 以考察共缺率与共缺机制对辅助变量作用的影响。当然共缺率很高的情况在实践中并不常见, 因此本研究设置的共缺率更具有实践指导意义。第二, 虽然本模拟研究表明辅助变量与研究变量存在共缺时, 样本量并非越大越好, 但对于多大的样本量是合适的,本研究并不能提供明确的参考。第三, 本研究主要模拟结构方程模型下辅助变量的效用, 对于结果能否推广到其他模型仍有待进一步的研究。另外, 本研究模拟的数据服从正态分布, 而实际研究中数据满足正态性的情况相对较少, 以后的研究可以考虑数据非正态的情况。总之, 本研究在前人研究的基础上对缺失值建模进行了更深入的分析, 当然缺失值建模领域尚存很多问题需要探索。

致谢

：作者非常感谢美国亚利桑那州立大学的Craig Enders博士在研究设计和数据模拟过程中给予的指导和帮助。作者同时感谢审稿专家在本文审稿过程中给予的指导和建议。Arbuckle, J. L. (1996). Full information estimation in the presence of incomplete data.

Advanced Structural Equation Modeling: Issues and Technique

s,

3

, 243–277.Collins, L. M., Schafer, J. L., & Kam, C. M. (2001). A comparison of inclusive and restrictive strategies in modern missing data procedures.

Psychological Methods, 6

, 330–351.Enders, C. K. (2006). Analyzing structural equation models with missing data. In G. Hancock & R. Mueller (Eds.),

Structural Equation Modeling: A Second Course

(pp. 313–342). Greenwich, CT: Information Age.Enders, C. K. (2008). A note on the use of missing auxiliary variables in full information maximum likelihood-based structural equation models.

Structural Equation Modeling,15

, 434–448.Enders, C. K., & Bandalos, D. L. (2001). The relative performance of full information maximum likelihood estimation for missing data in structural equation models.

Structural Equation Modeling, 8

, 430–457.Enders, C. K., & Gottschall, A. C. (2011). Multiple imputation strategies for multiple group structural equation models.

Structural Equation Modeling, 18

, 35–54.Enders, C. K., & Peugh, J. L. (2004). Using an EM covariance matrix to estimate structural equation models with missing data: Choosing an adjusted sample size to improve the accuracy of inferences.

Structural Equation Modeling, 11

,1–19.Graham, J. W. (2003). Adding missing-data-relevant variables to FIML-based structural equation models.

Structural Equation Modeling, 10

, 80–100.Graham, J. W. (2009). Missing data analysis: Making it work in the real world.

Annual Review of Psychology, 60

, 549–576.Hardt, J., Herke, M., & Leonhart, R. (2012). Auxiliary variables in multiple imputation in regression with missing X: A warning against including too many in small sample research.

BMC Medical Research Methodology, 12

, 184–196.Kidger, J., Heron, J., Leon, D. A., Tilling, K., Lewis, G., &Gunnell, D. (2015). Self-reported school experience as a predictor of self-harm during adolescence: A prospective cohort study in the South West of England (ALSPAC).

Journal of Affective Disorders, 173

, 163–169.Mustillo, S. (2012). The effects of auxiliary variables on coefficient bias and efficiency in multiple imputation.

Sociological Methods & Research, 41

, 335–361.Muthén, B., Kaplan, D., & Hollis, M. (1987). On structural equation modeling with data that are not missing completely at random.

Psychometrika, 52

, 431–462.Muthén, L. K., & Muthén, B. O. (1998–2010).

Mplus user’s guide

(6th ed.). Los Angeles: Muthén & Muthén.Muthén, L. K., & Muthén, B. O. (2002). How to use a Monte Carlo study to decide on sample size and determine power.

Structural Equation Modeling, 9

, 599–620.Newman, D. A. (2003). Longitudinal modeling with randomly and systematically missing data: A simulation of ad hoc,maximum likelihood, and multiple imputation techniques.

Organizational Research Methods, 6

, 328–362.Raykov, T. (2011). On testability of missing data mechanisms in incomplete data sets.

Structural Equation Modeling, 18

,419–429.Rubin, D. B. (1976). Inference and missing data.

Biometrika,63

, 581–592.

Schafer, J. L. (1999). NORM: Multiple imputation of incomplete multivariate data under a normal model [Computer software]. University Park: Pennsylvania State University,Department of Statistics.

Schafer, J. L., & Graham, J. W. (2002). Missing data: Our view of the state of the art.

Psychological Methods, 7

,147–177.Sun, J., Jin, Y. J., & Dai, M. F. (2013). Discussion on testing the mechanism of missing data.

Mathematics in Practice and Theory, 43

, 166–173.[孙婕, 金勇进, 戴明锋. (2013). 关于数据缺失机制的检验方法探讨.

数学的实践与认识,

43, 166–173.]Von Hippel, P. T. (2007). Regression with missing Ys: An improved strategy for analyzing multiply imputed data.

Sociological Methodology, 37

, 83–117.Wang, M. C. (2014).

Latent variable modeling with Mplus

.Chongqing, China: Chongqing University Press.[王孟成. (2014).

潜变量建模与Mplus应用

. 重庆: 重庆大学出版社.]Wang, M. C., & Ye, H. S. (2014). Planned missing data design:Through intended missing data make research more effective.

Advances in Psychological Science, 22

, 1025– 1035.[王孟成, 叶浩生. (2014). 计划缺失设计——通过有意缺失让研究更高效.

心理科学进展, 22

, 1025–1035.]Yoo, J. E. (2009). The effect of auxiliary variables and multiple imputation on parameter estimation in confirmatory factor analysis.

Educational and Psychological Measurement, 69

,929–947.Yuan, K. H., & Lu, L. (2008). SEM with missing data and unknown population distributions using two-stage ML:Theory and its application.

Multivariate Behavioral Research,43

, 621–652.Yuan, K.-H., Yang-Wallentin, F., & Bentler, P. M. (2012). ML versus MI for missing data with violation of distribution conditions.

Sociological Methods & Research, 41

, 598–629.