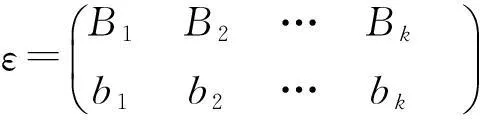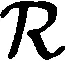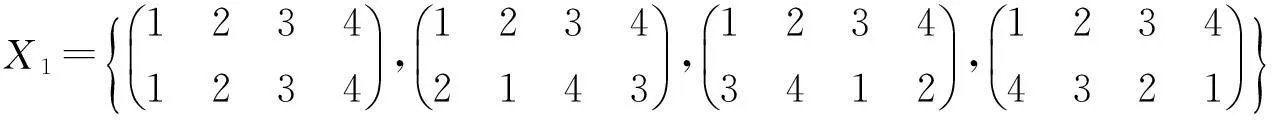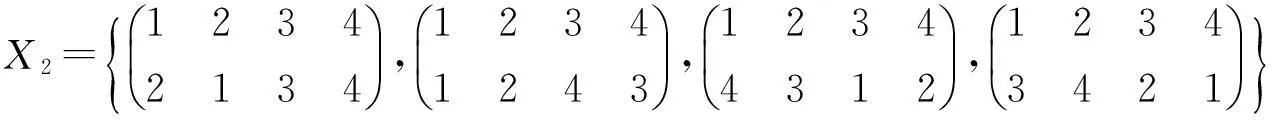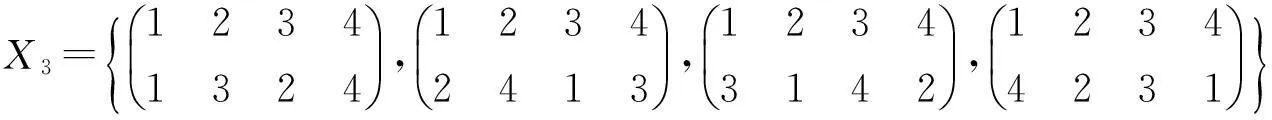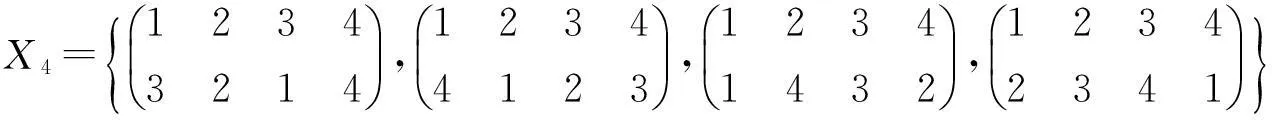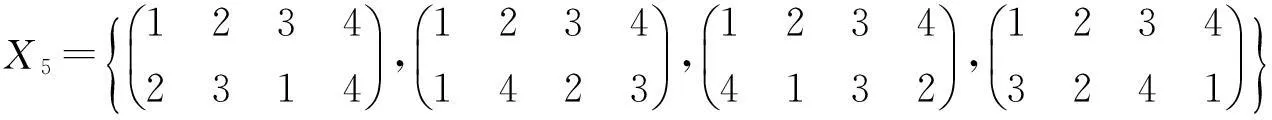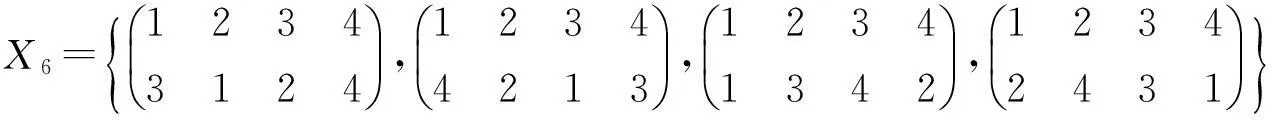两个全变换半群之间的同态I

唐　慧,杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

两个全变换半群之间的同态I

唐慧,杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

摘要：设Tn是Xn={1,2,…,n}上的全变换半群.Tm是Xm={1,2,…,m}上的全变换半群,本文刻画出当n>m时,Tn到Tm的所有同态,且还得到Tm为Tn的同态像的条件.

关键词：全变换半群;同态;同余

收稿日期：2015-01-05

通信作者：杨秀良(1963—)，男，教授，主要从事半群代数研究.E-mail:yxl@hznu.edu.cn

doi:10.3969/j.issn.1674-232X.2015.05.014

中图分类号:O152.7MSC2010: 43A22

文献标志码:A

文章编号:1674-232X(2015)05-0527-04

1引言和结论

设Tn是Xn上的全变换半群,它的许多性质已经被前人研究[1-5].特别的,在1998年Schein.B.M.和Teclezghi.B.[1]刻画出了Tn的所有自同态.在2012年黄丽丽和杨秀良在文[2]中刻画出了Tn的奇异部分的自同态.在2013年林双和杨秀良在文[3]中刻画出了全变换半群Tn和对称逆半群ISn之间的同态.接下来我们自然去研究两个全变换半群Tn和Tm之间的同态.在本文中我们将刻画出当n>m时,Tn到Tm的所有同态,且还得出Tm为Tn同态像的条件.

在本文中我们使用的映射为左映射.用Sn,An分别表示n次对称群和n次交错群.为完整叙述结果需引入如下三个映射.

(1)令ε为Tm中的一个幂等元.定义映射Φε:Tn→Tm为:对任意的α∈Tn,Φε(α)=ε.

(2)令ε,δ为Tm中两个不同的幂等元,且满足条件εδ=δε=δ.定义映射Ψε,δ:Tn→Tm如下:

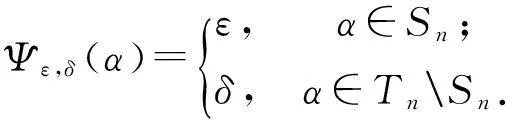
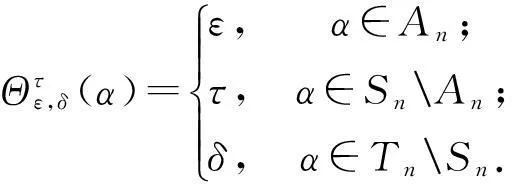
我们的主要结果如下

定理1设n>m,且令φ是Tn到Tm的任一映射,则φ是同态当且仅当φ为如下形式之一:

(1)Φε,其中ε为Tm中的一个幂等元;

(2)Ψε,δ,其中ε,δ为Tm中两个不同的幂等元,且满足条件εδ=δε=δ;

推论1Tm为Tn的同态像,则m=n或者m=1.

2结论的证明

为叙述方便,令α∈Tn,记im(α)={α(x)|x∈Xn},rank(α)=|im(α)|,ker(α)={(x,y)∈Tn×Tn|α(x)=α(y)}.于是全变换半群Tn上的Green[4]关系如下:任取α,β∈Tn,有

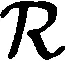
(2)αβ当且仅当ker(α)=ker(β);

为证明我们的结论,需要引入如下4个引理.

令α,β∈Tn,且α,β有如下形式:

(1)

(1)若rank(α)

(2)若rank(α)>k,则α≡Rβ当且仅当α=β;

引理2([4],Lemma7.4.2)n>1,Tn中不包含任何元素α使得对任意的π∈Sn满足πα=α.

引理3令ε是Tn的一个幂等元.则

(i)Tn的包含ε的一个极大子群Gε为

Gε={α∈Tn|im(α)=im(ε),ker(α)=ker(ε)}.

证明(i)由前面提到的全变换半群上的Green关系的性质直接得到.

(ii)令幂等元

其中bi1,bi2,…,bik是b1,b2,…,bk的一个排列.定义映射

便知φ是一个双射,且易验证Φ保持运算,因此Φ为同构.

定理1的证明易证定理1中给出的三种类型的映射都为Tn到Tm的同态,因此只需证明Tn到Tm的所有同态都具有定理1所给出的三种类型的映射的其中某种形式.

现令φ为Tn到Tm的任一个同态,由于ker(φ)为Tn上的一个同余,于是据引理1,分两种情况如下:

情况1ker(φ)是泛同余,则φ把Tn映到Tm中的某个幂等元,令这个幂等元为ε,从而φ为常量同态,且φ为定理1中的形式(1);

综上,当n≠4时,φ只具有定理1中的三种类型的映射的某种形式.

即Klien四元群.K4在S4中的6个陪集如下

φ(αβ)=φ(α)φ(β)=φ(α)ξ=ξ,

综上,当n=4时,φ只具有定理1中的三种类型的映射的某种形式.

推论1的证明若φ为Tn到Tm的满同态,则n≥m,进而如果n=m,则取φ为Tn的自同构即可.下面考虑1≤m≤n-1的情况,由定理1的证明知|Tm|≤3,而|T2|=4,则只能取m=1.

参考文献:

[1] Schein B M, Teclezghi B. Endomorphisms of finite full transformation semigroups [J]. Proceedings of the American Mathematical Society, 1998, 126(9):2579-2587.

[2] 黄丽丽,杨秀良.全变换半群的奇异部分的自同态[J].杭州师范大学学报:自然科学版,2012,11(3):249-253.

[3] 林双,杨秀良.全变换半群Tn与对称逆半群ISn之间的同态[J].浙江大学学报:理学版,2013,40(2):123-126.

[4] Ganyushkin O, Mazorchuk V. Introduction to Classical Finite Transformation Semigroups [M]. London: Springer Verlag,2009.

[5] Howie J M． Fundamentals of semigroups theory[M]． Oxford: Oxford University Press，1995．

Homomorphisms of Two Finite Full Transformation Semigroups I

TANG Hui, YANG Xiuliang

(College of Sciences, Hangzhou Normal University, Hangzhou 310036, China)

Abstract:Let Tnbe the full transformation semigroup on a finite set Xn={1,2,n}. Let Tmbe the full transformation semigroup on a finite set Xm={1,2,m}. This paper describes all homomorphisms from Tnto Tmwhen n>m, and gets the conditions that Tmis the homomorphic image of Tn.

Key words:full transformation semigroup; homomorphism; congruences

第14卷第5期2015年9月杭州师范大学学报(自然科学版)JournalofHangzhouNormalUniversity(NaturalScienceEdition)Vol.14No.5Sep.2015