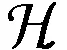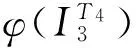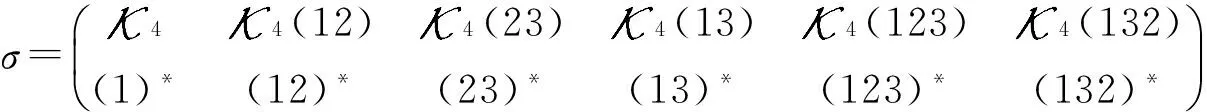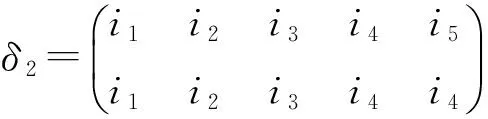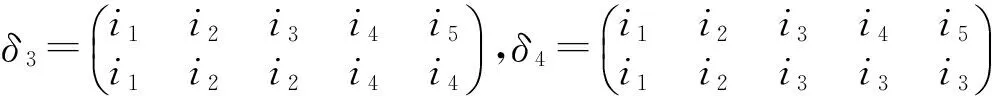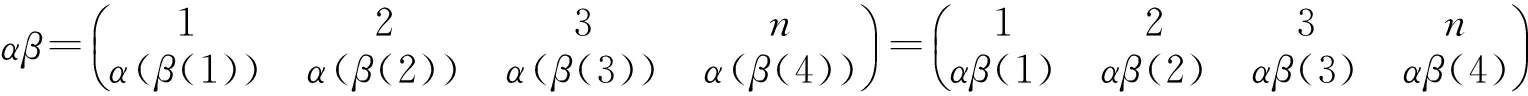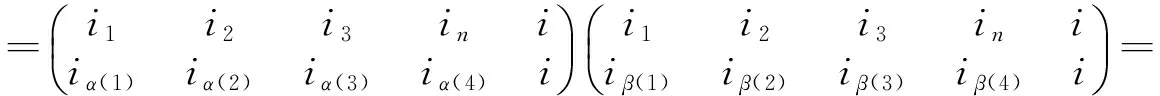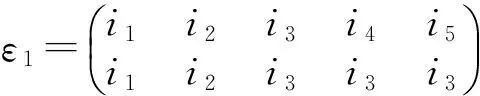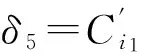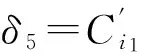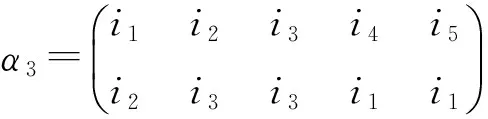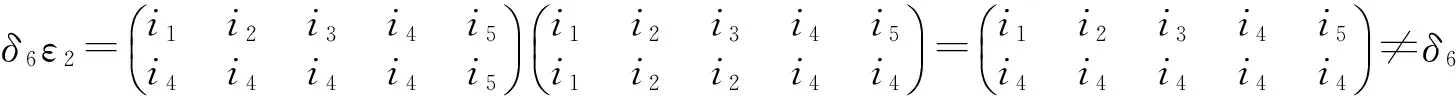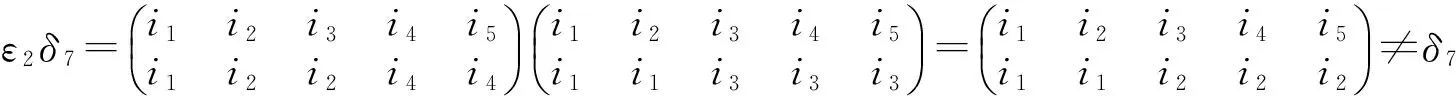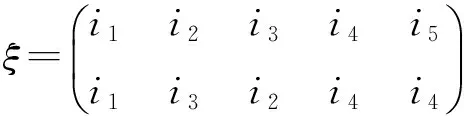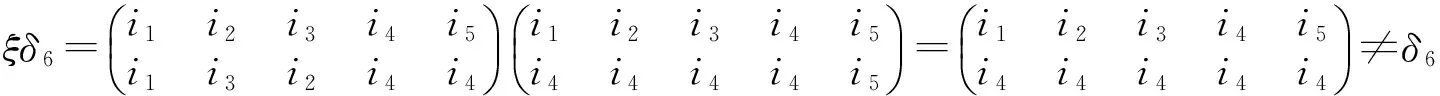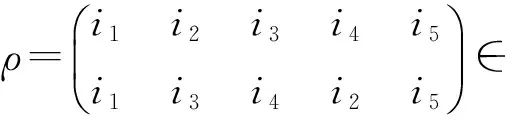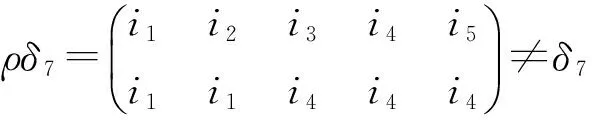全变换半群T4到T5的同态

唐　慧, 杨秀良

(杭州师范大学理学院,浙江 杭州 310036)



全变换半群T4到T5的同态

唐慧, 杨秀良

(杭州师范大学理学院,浙江 杭州 310036)

设n是一个大于等于1的正整数,Tn是Xn={1,2,…,n}上的全变换半群,Tn+1是Xn+1={1,2,…,n+1}上的全变换半群,本文刻画出当n=4时,T4到T5的所有同态.

全变换半群;同态;同余

1　引言和结论

设Tn是Xn上的全变换半群,在1998年Schein B M和Teclezghi B[1]刻画出Tn的所有自同态.接下来我们自然去研究两个全变换半群Tn和Tm之间的同态.当n>m时的同态已经研究出来[2],且在不考虑n=4的情况下Tn到Tn+1的所有同态也已经研究出来[3].在本文中将刻画出当n=4时,T4到T5的所有同态.

1) 令ε为T5中的一个幂等元.定义映射Φε:T4→T5为:对任意的α∈T4,Φε(α)=ε.

2) 令ε,δ为T5中两个不同的幂等元,且满足条件εδ=δε=δ.定义映射Ψε,δ:T4→T5如下:

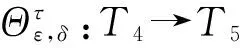
我们的主要结果如下

定理1(i)取定i∈X5,定义Φi为T4到T5的一个映射如下:首先规定

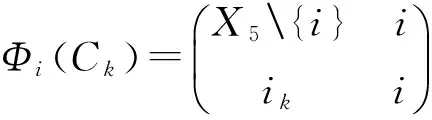
其中k∈X4,{i1,i2,i3,i4}=X5{i},然后任取α∈T4{C1,C2,C3,C4},规定

则Φi为T4到T5的一个单同态.

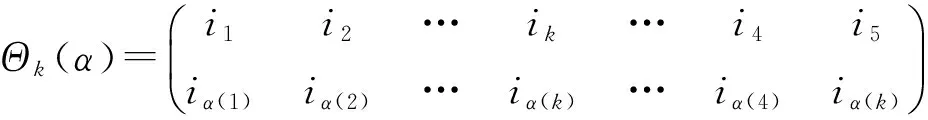
则Θk为T4到T5的一个单同态.

反之,T4到T5的任一个单同态φ都具有形式(i)或者(ii).

(iii)当φ为非单时,则φ是同态当且仅当φ为如下形式之一:

(1)Φε,其中ε为T5中的一个幂等元;

(2)Ψε,δ,其中ε,δ为T5中两个不同的幂等元,且满足条件εδ=δε=δ;

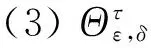
C

2　结论的证明

为叙述方便,令α∈Tn,记im(α)={α(x)|x∈Xn},rank(α)=|im(α)|,ker(α)={(x,y)∈Tn×Tn|α(x)=α(y)}.于是全变换半群Tn上的Green[4-5]关系如下:任取α,β∈Tn,有

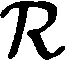
为证明我们的结论,需要引入如下两个引理.

令α,β∈Tn,且α,β有如下形式:

(1)

1)若rank(α)

2)若rank(α)>k,则α≡Rβ当且仅当α=β;

则rankδ≤2.

若rankδ=5,则由δ为T5中的幂等元知δ有如下形式

其中{i1,i2,…,i5}=X5,从而由αδ1=δ1α=δ1可知

α(i1)=i1,α(i2)=i2,α(i3)=i3,α(i4)=i4,α(i5)=i5,

进而{α∈T5|αδ=δα=δ}={δ}没有与S3同构的子群,矛盾.

若rankδ=4,则δ有如下形式

其中{i1,i2,…,i5}=X5,从而由αδ2=δ2α=δ2可得

α(i1)=i1,α(i2)=i3α(i3)=i3,α(i4)=i4,α(i5)∈{i4,i5},

若rankδ=3,则δ有如下两种形式

其中{i1,i2,…,i5}=X5.若δ=δ3,则由αδ3=δ3α=δ3可得

α(i1)=i1,α(i2)=i2,α(i4)=i4,

α(i3)∈{i2,i3},α(i4)∈{i4,i5},

定理1的证明易证定理1中(iii)的映射都为T4到T5的同态.下面验证Φi和Θk都是T4到T5的单同态.

任取α∈T4,β∈T4,且

从而

则由Φi的定义知

其中{i1,i2,i3,i4}=X5{i},从而

因此Φi(α)Φi(β)=Φi(αβ),所以Φi是T4到T5的一个同态,又令Φi(α)=Φi(β),从而α(x)=β(x),其中x∈X4,进而Φi是单的,故Φi是T4到T5的一个单同态.同理可证Θk是T4到T5的一个单同态.

现令φ为T4到T5的任一个同态,由于ker(φ)为T4上的一个同余,于是据引理1分两种情况如下.

情况1ker(φ)是泛同余,则φ把T4映到T5中的某个幂等元,令这个幂等元为ε,从而φ为常量同态,且φ为定理1中形式(iii)中的(1);

其中{i1,i2,…,i5}=X5.下面根据δ的形式先对ε1进行讨论.

若δ为δ6这种形式,则

矛盾.又

矛盾.故ε不能为ε1这种形式.

若δ=δ6,则

矛盾.又

矛盾.故ε也不能为ε2这种形式.

其中{i1,i2,…,i5}=X5.下面对δ的形式进行讨论.

则

故φ具有形式(4.1).

则

[1] SCHEIN B M, TECLEZGHI B. Endomorphisms of Finite Full Transformation Semigroups [J]. Proceedings of The American Mathematical Society,1998,126(9):2579-2587.

[2] 唐慧,杨秀良.两个全变换半群之间的同态I[J].杭州师范大学学报(自然科学版),2015,14(5):527-530.

[3] 唐慧,杨秀良.两个全变换半群之间的同态II[J].杭州师范大学学报(自然科学版),2016,15(2):67-72.

[4] GANYUSHKIN O, MAZORCHUK V. Classical Finite Transformation Semigroups [M]. London: Springer Verlag,2009.

[5] DOSS C. Certain equivalence relation in transformation semigroups [D]. Nashville: Univ of Tennessee,1955.

[6] Mal’tsev A I. Symmetric groupoids [J]. Mat Sbornik N S,1952,73(1):136-151.

The Homomorphisms of Full Transformation SemigroupT4toT5

TANG Hui, YANG Xiuliang

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

Letnbe a positive integer greater than or equal to 1,Tnbe the full transformation semigroup on a finite setXn= {1,2,…,n}. LetTn+1be the full transformation semigroup on a finite setXn+1={1,2,…,n+1}. This paper describes all homomorphisms fromT4toT5whenn=4.

full transformation semigroup; homomorphism; congruence

2015-11-22

杨秀良(1963—)，男，教授，主要从事半群代数研究.E-mail:yxl@hznu.edu.cn

10.3969/j.issn.1674-232X.2016.05.014

O152.7MSC2010:43A22

A

1674-232X(2016)05-0526-07