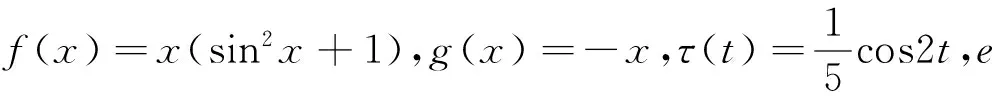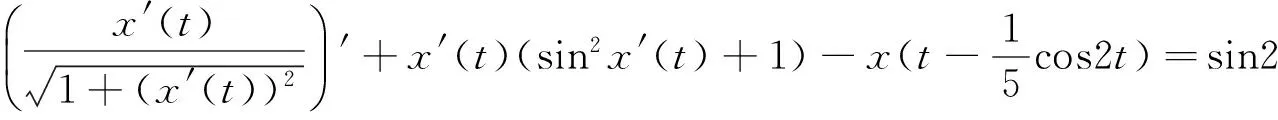一类Rayleigh型平均曲率方程周期解存在与唯一性
陈文斌, 张 猛
(武夷学院数学与计算机学院,福建 武夷山 354300)
一类Rayleigh型平均曲率方程周期解存在与唯一性
陈文斌, 张猛
(武夷学院数学与计算机学院,福建 武夷山 354300)
运用重合度理论和一些新的分析方法探讨了一类Rayleigh型平均曲率方程周期解存在性与唯一性问题,得到了一些相应的新结果并举例说明其结果的有效性.
周期解;平均曲率;重合度定理;Rayleigh
0 引 言
近年来,许多学者运用Mawhin重合度拓展定理对平均曲率方程周期解存在性问题的研究获得了很多结果[1-5].例如,在文献[1]中,Li研究了一类具时滞Rayleigh型平均曲率方程
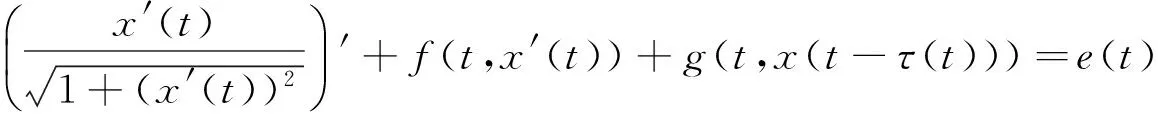
(1)
通过转化,将(1)转化等价方程组,
(2)
利用重合度理论,得到了方程组(2)至少存在一个T-周期解,从而解决了方程(1)的周期解问题.方程组(2)先验界估计的过程中,需满足条件|y|0<1.但文献[1]中并没有去验证这个条件.梁在文献[2]中研究了一类具有偏差变元的广义平均曲率方程周期解问题,方程如下:
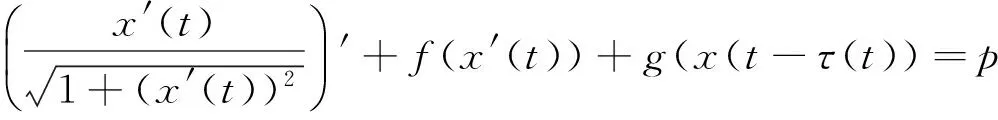
(3)
对于方程(3),如果下列条件成立:
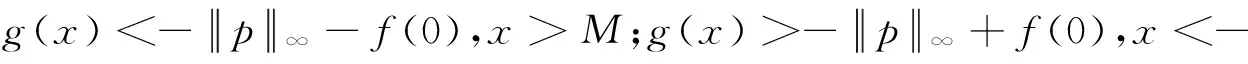
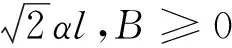
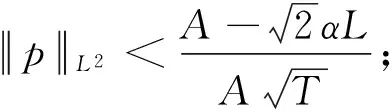
则问题(3)至少存在一个T-周期解.很明显,作者对于问题(3)的解决给了足够复杂和较多的条件,尤其是条件(A3)非常强,在该文章中,这个条件是用来验证先验界估计{Ω⊂{(x1,x2)T∈X:|x1|0 受到上述文献研究问题的启发,我们通过使用Mawhin重合度理论和运用一些技巧解决了下列一类具有时滞Rayleigh型平均曲率方程 (6) 周期解存在性问题,其中f,g,e∈C(R,R).此外,还证明了该方程周期解唯一性问题.最后,用一实例来说明所得结果的有效性. 1)对任意的λ∈(0,1),x∈∂Ω∩D(L),均有Lx≠λNx; 2)对任意的x∈KerL∩∂Ω,均有QNx≠0; 引理2[7]如果u:R→R是在R上是连续可微的且a>0,则有下列不等式成立: 为了应用引理1,研究下列方程组 (7) X=Y={x|x=(x1(t),x2(t))Τ∈C(R,R2),x(t)=x(t+T)}, 其中D(L)={x|x=(x1(t),x2(t))Τ∈C1(R,R2),x(t)=x(t+Τ)}. 又因为 令 其中 首先,为了方便,我们给出下列条件 证明为了使用引理1,考虑下列方程组 (8) 其中λ∈(0,1),将方程组(8)的第一个式子代入到第二式,得到 (9) (10) 即 (11) 从式(11),知道 (12) 在方程(9)两边同时乘以x1(t)且在[0,T]上积分得 (13) 由于 (14) (15) (16) 把式(14)(15)(16)代入式(13),有 (17) 式(17)这意味着必存在一个正常数d1使得 (18) 根据引理2,有下列等式 (19) 把式(12)(18)代入到式(19),很明显存在一个正常数D,使得 |x1|0 (20) 下面,我们来证明|x2|0<1. 由于|x1|0 |-g(x(t-τ(t)))+e(t)| 下面,用反证法证明 (21) f(x)≥cx, 若式(21)不成立,则总存在t2>t1这样的时刻,使得 (22) 且对于任意的t∈(t1,t2),都有 (23) 这与式(22)矛盾,所以式(21)成立.类似地,可以证明第二种情况,当x<0时 (24) (25) 即 (26) 在式(26)的第二个式子,两边同时乘以c1,得 因此 H(v,μ):(Ω∩KerL)×[0,1]→R:H(v,μ)=μ(x,y)T+(1-μ)JQN(v), deg{JQN,Ω∩KerL,0}=deg{H(v,0),Ω∩KerL,0}=deg{H(v,1),Ω∩KerL,0}≠0. 下面,我们来证明问题(6)周期解得唯一性. y3(t)=φ-1(x3(t)),y4(t)=φ-1(x4(t)), 且 u(t)=x3(t)-x4(t),v(t)=y3(t)-y4(t). 现在用反证法证明u(t)≤0,∀t∈[0,T]的情形,若不满足u(t)≤0,∀t∈[0,T],则存在一个t0∈[0,T]使得 所以u′(t0)=φ(y3(t0))-φ(y4(t0))=0,这表示y3(t0)=y4(t0)且u″(t0)≤0.但是 u″(t0)= φ′(y3(t0))-φ′(y4(t0))= (27) 知式(27)与假设相矛盾,所以u(t)≤0,∀t∈[0,T].类似地,同样可证明u(t)≥0,∀t∈[0,T],所以u(t)≡0,即x3(t)=x4(t), 这样唯一性证毕. (28) [1] LI J, LUO J L, CAI Y. Periodic solutions for prescribed mean curvature Rayleigh equation with a deviating argument[J]. Adv Differ Equ,2013,2013(1):1-11. [2] 梁载涛,鲁世平.具偏差变元的广义平均曲率方程周期解问题[J].四川大学学报(自然科学版),2014,51(2):240-247. [3] LI Z Y, AN T Q, GE W G. Existence of periodic solutions for a prescribed mean curvature Lienard p-Laplaceian equation with two delays[J]. Adv Differ Equ,2014,2014(1):1-10. [4] WANG D S. Existence and uniqueness of periodic solutions for prescribed mean curvature Rayleigh type p-Laplaceian equation[J]. J Appl Math Comput,2014,46(1-2):181-200. [5] FENG M Q. Periodic solutions for prescribed mean curvature Lienard equation with a deviating argument[J].Nonlinear Anal: Real Word Appl,2012,13(3):1216-1223. [6] GAINES R E, MAWHIN J L. Coincidence degree and Nonlinear Differential equation[M]. Berlin: Springer,1977. [7] TANG X H, XIAO L. Homoclinic solutions for ordinaryp-Laplacian systems with a coercive potential[J]. Nonlinear Anal: Theory, Methods and Applications,2009,71(3):1124-1132. Existence and Uniqueness of Periodic Solutions for Rayleigh Mean Curvature Equation CHEN Wenbin, ZHANG Meng (College of Mathematics and Computer Science, Wuyi University, Wuyishan 354300, China) In this paper, by using coincidence degree theory and some analysis methods, the existence and uniqueness of periodic solutions for Rayleigh mean curvature equation is studied. Some new results are obtained and demonstrated. periodic solution; mean curvature; coincidence degree theory; Rayleigh 2015-11-15 福建省中青年教师教育科研项目(JA15524);武夷学院青年教师科研项目(XQ201305). 陈文斌(1986—),男,助教,硕士,主要从事微分方程及其应用研究.E-mail:cwb210168@126.com. 10.3969/j.issn.1674-232X.2016.05.016 O175.1;O177.92MSC2010:34K13 A 1674-232X(2016)05-0542-071 主要引理
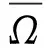
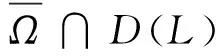
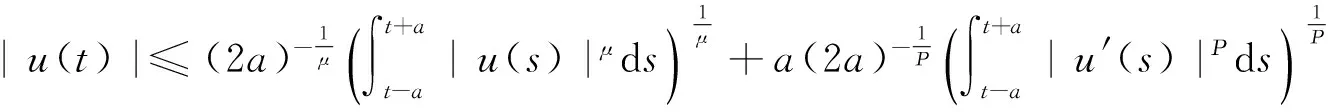

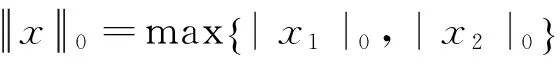
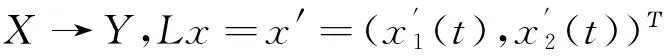
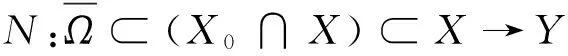

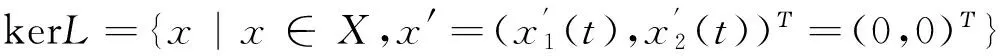

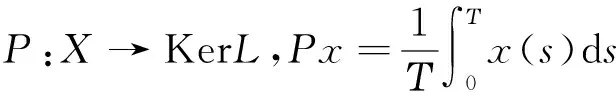
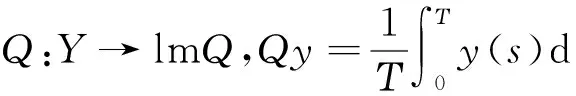
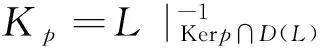
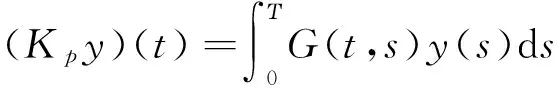
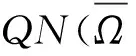
2 主要结果

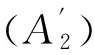
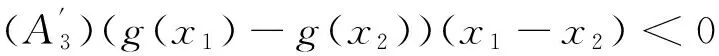
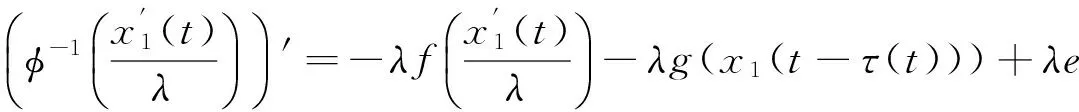
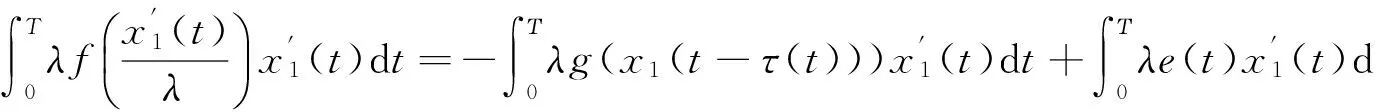
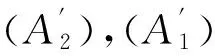

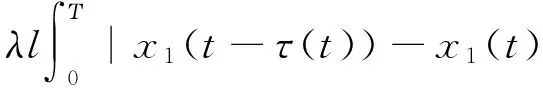



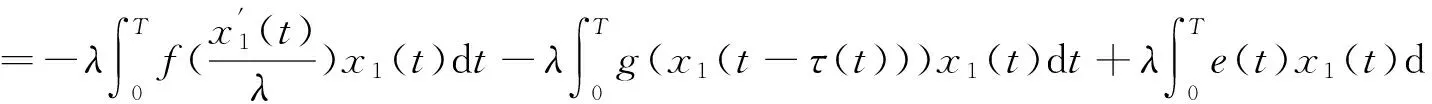

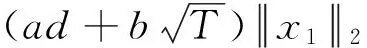
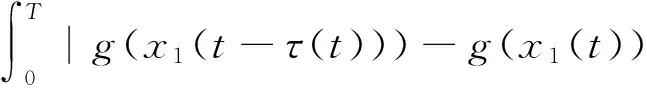

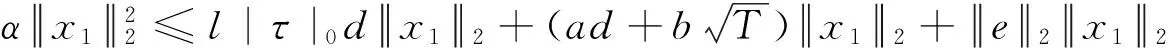
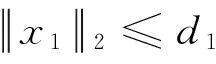




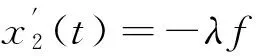
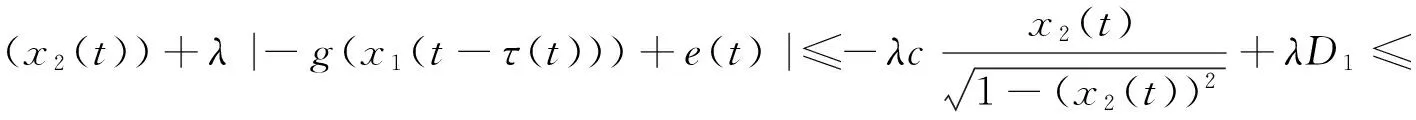
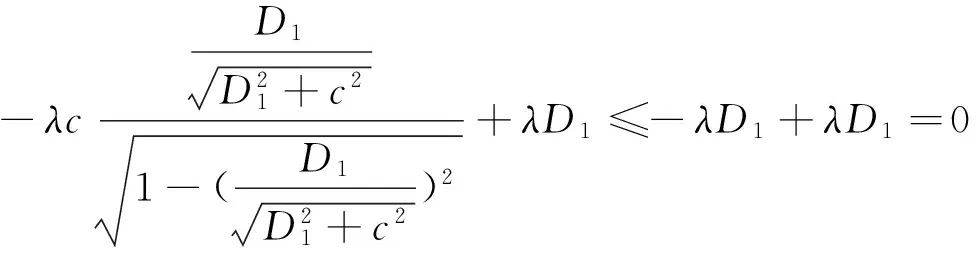
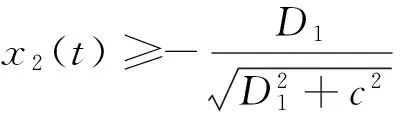

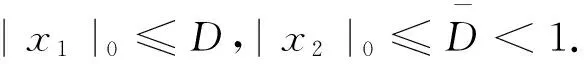
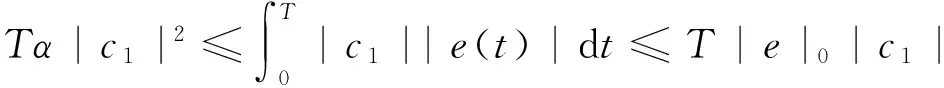
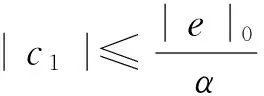
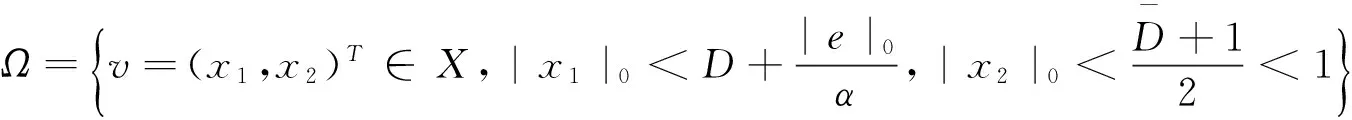

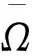

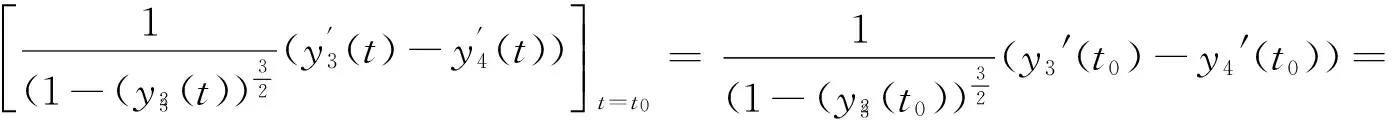
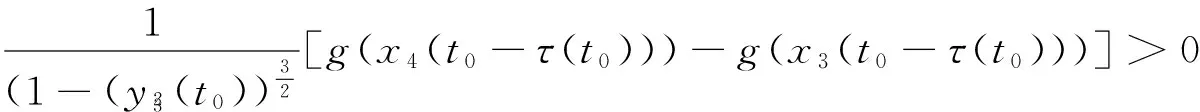
3 应用举例