海上蒸发波导预测模型选择方法

周　朋，刘光辉

(解放军91404部队，秦皇岛 066001)



海上蒸发波导预测模型选择方法

周朋，刘光辉

(解放军91404部队，秦皇岛 066001)

摘要：基于水文气象条件的蒸发波导预测方法是一种常用的蒸发波导预测方法。在对现有典型方法的敏感性、稳定性、适应性以及优缺点进行了详细的比较分析基础上，提出海上舰艇蒸发波导预测模型选择方法，从理论研究到实验数据的对比分析表明该方法具有明显的优势，对提高海上蒸发波导预测能力具有重要意义。

关键词：蒸发波导；预测模型；选择方法

0引言

关于用水文气象条件预测蒸发波导模型，国外许多专家在上世纪70年代初已经开始这方面的研究，比较有代表性的预测模型有美国的 Paulus-Jeske提出并不断修正的蒸发波导预测模型(P-J模式)[1-2]、法国学者Luc Musson-Genon，Sylvie Gauthier和Eric Bruth提出的MGB模式[3]以及美国霍谱金斯大学的S.M.Babin提出的Babin模式[4](也称A模式)。我国在蒸发波导预测上比较有代表性的研究成果有刘成国提出的伪折射率模式[5]和李云波提出的基于海气通量算法的蒸发波导诊断模型[6]，他们提出的各种模型都是在Monin-Obukhov相似理论的基础上得到的，只是应用不同。为弥补Monin-Obukhov相似理论在某些条件下不能使用的缺陷，戴福山提出了利用局地相似理论代替Monin-Obukhov相似理论确定蒸发波导的方法，称为局地相似蒸发波导模式[7]。此外，我国的很多学者还对几种传统模式在我国海域的适应性进行了研究[8]，对蒸发波导预测模型在我国海域的应用研究起到了促进作用。本文对传统的基于水文气象条件预测蒸发波导模型进行综合比较分析，提出了海上舰艇预测蒸发波导模型的选择方法。

1传统预测模型

1.1　 Monin-Obukhov相似理论

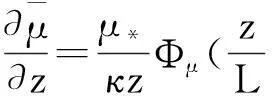
(1)

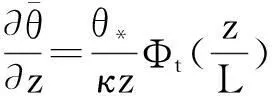
(2)

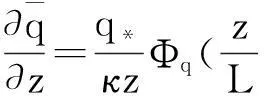
(3)

式中:μ*、θ*、q*分别为速度特征尺度、温度特征尺度、水汽特征尺度;κ为Karman常数，取κ=0.4;L为长度特征尺度，称为Monin-Obukhov长度;Ζ=z/L,为层结稳定度参数，当ζ>0时，为稳定层结；ζ<0时，为不稳定层结；ζ=0时，为中性层结;Φμ、Φt、Φq为稳定度参数ζ的函数，称为普适函数，不同研究人员根据观测资料给出的普适函数不同，在中性层结下均等于1[9]。

对式(3)进行积分，取风速为0，则有：

(4)

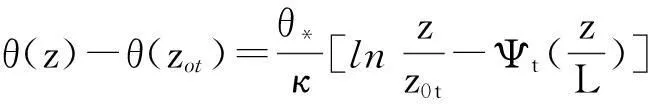
(5)

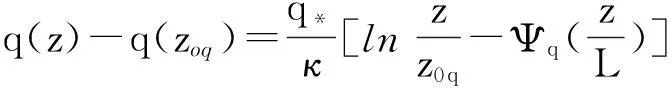
(6)

式(1)～(3)及式(4)～(6)称为Monin-Obukhov相似理论关系式。

1.2　传统模型

(1) P-J模式[7]

在利用P-J模式进行蒸发波导预测的过程中，引入了不随气压变化的位折射指数Np，其关系式如下[9]:

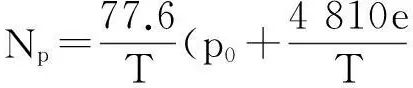
(7)

由Monin-Obukhov相似理论的推导可知，位折射指数垂直梯度dNp/dz满足：

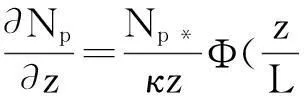
(8)

当位折射指数梯度等于临界位折射指数梯度b时，所对应的高度即为蒸发波导高度d。

因此，在稳定或者中性层结条件下：

(9)

对于不稳定层结条件下：

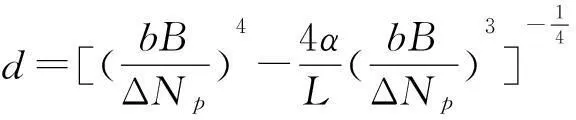
(10)

由于Monin-Obukhov相似理论不能适用于极端稳定和极端不稳定层结的海洋大气环境，因此，在极端稳定层结环境下建议d/L应不大于1，否则令其等于1；极端不稳定层结环境下令蒸发波导高度为零。

(2) MGB模式[3,7,10-13]

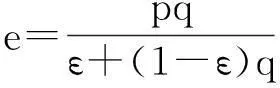
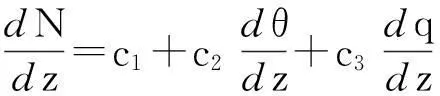
(11)

式中:dθ/dz、dq/dz利用Monin-Obukhov相似理论计算获得。

与P-J模式不同的地方在于MGB模式在确定L与Ri关系以及特征尺度参数θ*、q*时，引用了隐函数的方法，计算出特征尺度参数θ*、q*值。最后采用解析方法计算得到波导的高度为：

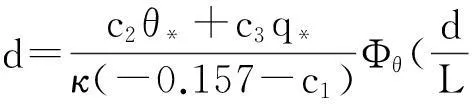
(12)

(3) Babin模式[4,7]

Babin模式最突出的贡献就是通过引入“阵风性”速度的概念，将Monin-Obukhov相似理论的适用性推广到了甚低风速条件下。

得到在稳定和中性大气层结条件下，预测的波导高度表达式为：

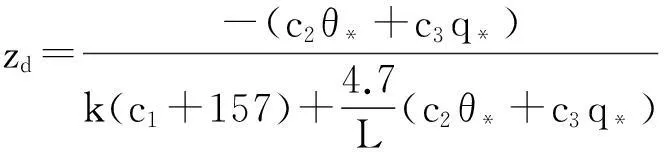
(13)

不稳定层结大气条件下的波导高度由下式确定：

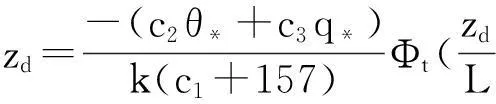
(14)

在极端不稳定层结环境下，Monin-Obukhov相似理论不再适用，该模式引入了“阵风性”速度ωg，海面平均风速为：

S=μ2+ω2

(15)

(4) 伪折射率模式[5]

伪折射率模式是由我国学者刘成国提出并验证其可行性的。伪折射率Np定义如下：

Np=4.495e-1.263T

(16)

该模式最终给出的蒸发波导环境下大气修正折射指数关系式如下：

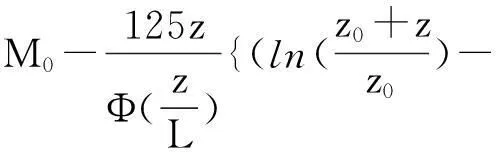
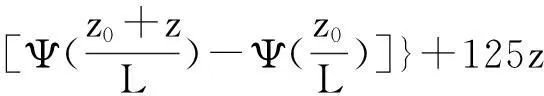
(17)

并采用测得环境参数，利用迭代法即可得到波导高度。

(5) Flux模型[3,6]

Flux模式是基于通量算法的蒸发波导模型的简称，模型将相似理论与通量算法相结合，首先求得各气象要素垂直廓线分布，进而得到修正折射率廓线，根据修正折射率最小值对应的高度，确定波导高度[12]。

根据测得的海洋环境试验数据，该模型通过利用阵性风速ωg来提高适用性：

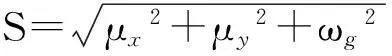
(18)

可以得到修正折射指数M的廓线，此时，最小值点所在高度即为蒸发波导高度。

(6) 局地相似模式和New模式[7]

局地相似蒸发波导模式和New模式是由我国专家戴福山在总结前人的基础之上提出的，既吸收了国内外最新模式的优点，同时又弥补了Monin-Obukhov相似理论在某些特殊条件下不能适用的不足。

New模式是对Babin模式和局地相似蒸发波导模式的综合，由于Babin模式没有考虑在强稳定层结条件下Monin-Obukhov相似理论不再适用时的修正，因此，New模式在具有稳定层结海洋大气环境时采用局地相似模式算法，具有不稳定层结海洋大气环境时采用Babin算法，这样即利用了Monin-Obukhov相似理论的优越性,又对极端条件下的波导预测进行了修正，因此，New模式是理论上较为优秀的模式。

1.3　敏感性分析

海上蒸发波导对大气环境的变化呈现出不同的变化特性，对不同大气环境特征的敏感性不同，对气象条件的敏感度从高到低依次是：大气湿度、气海温差、风速、气压[11]。蒸发波导敏感性最高的海洋大气环境因素是大气湿度，满足其他海洋环境因素相同的环境下，海洋气象环境中相对湿度越低时波导的绝对高度越大。蒸发波导敏感性次之的海洋大气环境因素是气海温差，随温差正值、负值不同而不同：气海温差大于零时，气海温差差值的大小对波导高度影响很大；当气海温差小于零时，气海温差差值的大小对波导高度影响较小。风速对蒸发波导影响的显著特点是风速越大，波导高度越低，尤其在低风速时影响效果更为明显。相对而言，蒸发波导敏感性最小的海洋大气环境因素是气压。

本文根据蒸发波导对不同海洋气象环境的敏感性分析，结合我国周边海域水文条件特点，对前人研究的不同蒸发波导预测模型在海洋大气环境中的敏感性、稳定性、适应性加以总结与分析，选择出较适合我国海域气象环境特征和舰载通信装备特点的蒸发波导预测模型。

2009年，左雷等人通过理论分析和实测实验数据对P-J模式的敏感性、适应性进行了研究，研究结果表明[4]：该模式计算得到的波导高度对海面风速、大气相对湿度的变化较为敏感，在其他海洋环境因素一定时波导高度湿度越大,波导高度越低，与实际蒸发波导敏感性特征相符，但在风速较大时模型计算结果的偏差较大；在不稳定层结海洋大气环境下，预测高度对气海温差变化较为敏感；相对湿度介于75%～85%之间的小风速海洋大气环境下,该模式计算结果与实际值偏差最小。

田斌等人对解析MGB预测模式在我国海区适应性也做了相关的研究，综合比较分析可以得出模型预测结果对气海温差的敏感性最大，其次是相对湿度和风速，气压敏感性最小；越接近中性层结，模型预测得到的波导高度值与实测真实值越接近。但国家海洋环境预报中心李诗明对MGB模式的研究可以看出，模型预测结果对输入变量噪声的敏感性很强，因此限制了该模式在业务上的使用[1]。

Babin模式最突出的特点是采用了盐度修正来计算饱和水汽压的值，并在一定程度上克服了Monin-Obukhov相似理论的局限性，将其适用性延伸至低风速的极端稳定层结海洋大气环境下。田斌等对该模式在我国海域的适应性及敏感性进行了分析和实验对比，结论为：该模式对气海温差、风速及大气相对湿度等海洋气象环境因素的变化都具备一定的敏感性，对水文气象观测系统的传感器具有最低精度要求[3]。

刘成国在提出伪折射率模型的同时对其敏感性和实验结果进行了分析[5]，计算机仿真结果表明:气海温差满足小于-1℃的海洋气象环境下，其对波导高度的影响不明显;而当气海温差在0～2℃时，影响变化显著，但变化规律不明显；南海海上实验利用测量仪器测得的蒸发波导在各种天气条件下的发生概率与利用伪折射率模型预测得到的波导发生概率相近,并且吻合度达到了52%以上。

Flux模式与Babin模式计算机理大致相同，都是通过海气通量算法计算Monin-Obukhov相似理论的相关参数，并且都引入了“阵风性”对在风速为零情况下Monin-Obukhov相似理论进行了修正，因此这2种模式的特点相似，在实际运用中根据大气环境条件和二者在其他方面的差异考虑即可。

在研究蒸发波导预测模型过程中，许多专家学者对各模型在海洋大气环境下的敏感性、稳定性等方面进行了比较分析，得出了许多的研究成果。戴福山分别于1999年和2000年先后5次进行海上试验，实际观测海洋水文气象数据，研究不同预测模型预测得到的波导高度，得出如下结论[7]：

对于较常见的不稳定层结、中性层结和弱稳定层结的海洋大气环境中，各模型预测得到的波导高度大致相同；对于晴好天气里经常发生强稳定层结海洋大气环境中，只有基于局地相似理论的local1模型和P-J模型预测结果比较准确，但在强稳定层结海洋大气环境中Monin-Obukhov相似理论是不适用的，P-J模式采用了人为修正。

评估电磁波传播损耗方面，当气海温差大于零时或者强稳定层结大气环境下，基于局地相似理论的local1模式可以较好地满足精确计算传输损耗的需要，P-J模式没有显示出超视距传输现象，其他模式结果也不够准确；在弱稳定层结条件、中性层结以及不稳定层结的海洋大气环境下,各模型之间预测得到的波导高度差异较小；而在风速较小时，Babin模式的预测结果较好。

王向敏结合我国海域实测数据对Babin模式与伪折射率模式进行了比较分析[1]，在风速较小时，Babin模式的稳定性明显优于伪折射率模式；两模式对湿度和温度的敏感性相同，但伪折射率模式对风速的敏感性较小。宋伟利用实验数据对P-J模式和Babin模式适应性进行了对比分析，分析结果表明[14]：按层结稳定性划分时，P-J模式的准确性要好于Babin模式；而当风速较小时，Babin模式计算的波导高度误差要小于P-J模式，进一步验证了低风速环境下Babin模式较其他方法预测结果的准确性更好。郭相明等人指出[15]：在具备稳定层结的海洋大气环境中，P-J模式预测精度最优；在不稳定层结的海洋大气环境中，MGB模式预测精度最低，其他模式相差不大，并提出在蒸发波导预测上优先考虑P-J模式。

2海上舰艇预测蒸发波导模型

2.1　预测模型选择方法

通过对基于水文气象环境传统预测模型的研究及前人对各个方法的比较分析可以看出，传统的预测模型在分析检测波导所处的近海面空间范围内的气象因素特征是基于Monin-Obukhov相似理论或局地相似理论来构建的；只是蒸发波导高度计算方法、普适函数选取依据、参量特征尺度等其他因素的选择上存在差异。本文在此基础上，根据海上舰艇装备实际情况，提出采取如下方式利用水文气象条件预测蒸发波导：

(1) 在强稳定层结海洋大气环境时，选取局地相似理论的蒸发波导预测模式;

(2) 在弱稳定层结、中性层结以及不稳定层结海洋大气环境时选取P-J模式;

(3) 在极端不稳定层结海洋大气环境时选取Babin模式。

Monin-Obukhov相似理论不满足强稳定层结海洋大气环境时的应用条件，P-J模式在此情况下需考虑人为修正，不适于舰艇装备及人员实际情况，而局地相似理论适用于整个近地层，可以弥补Monin-Obukhov相似理论的缺陷，因此本文在强稳定层结海洋大气环境时选取基于局地相似理论的蒸发波导预测模式。

极端不稳定层结多发生在晴好的海洋大气环境中，通过上述各个模式的研究与比较分析，Babin模式将Monin-Obukhov相似理论推广到甚低风速海洋大气环境下、风速较小的大气环境时，该模型预测效果最优。

其它大气层结的海洋大气环境下选用P-J模式。P-J模式是目前蒸发波导预测方面应用最成功的模型之一，美国研究人员将其集成到某微波传播预报系统中，作为业务化预报模式投入实际应用。可以看出，在P-J模式的应用上有着成熟的先例与经验，而且通过前面的比较分析，在弱稳定层结、中性层结以及不稳定层结的海洋大气环境时，该模式除在某些特定水文气象环境下具有优势外，其他环境条件下并无明显缺陷，因此，建议使用P-J模式。

2.2　对比分析

为进一步验证本文提出的蒸发波导预测模型选择方法的有效性，采用戴福山于2000年1月14日南海试验的海面水文气象数据及部分模型计算得到的蒸发波导(见参考文献[7]的238-239页)高度加以分析。实验数据如表1、表2所示。

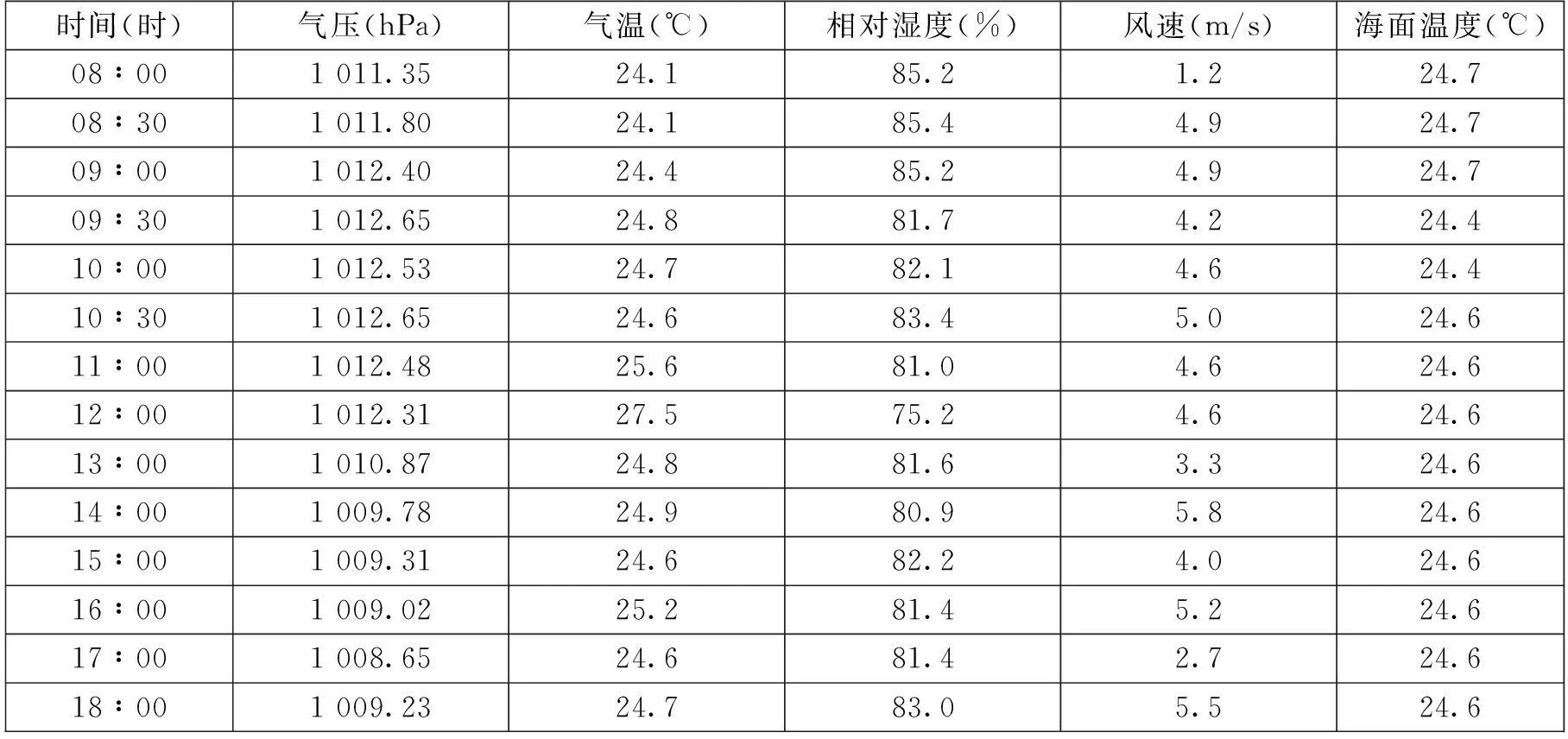
表1　2000年1月14日南海试验海面水文气象观测数据

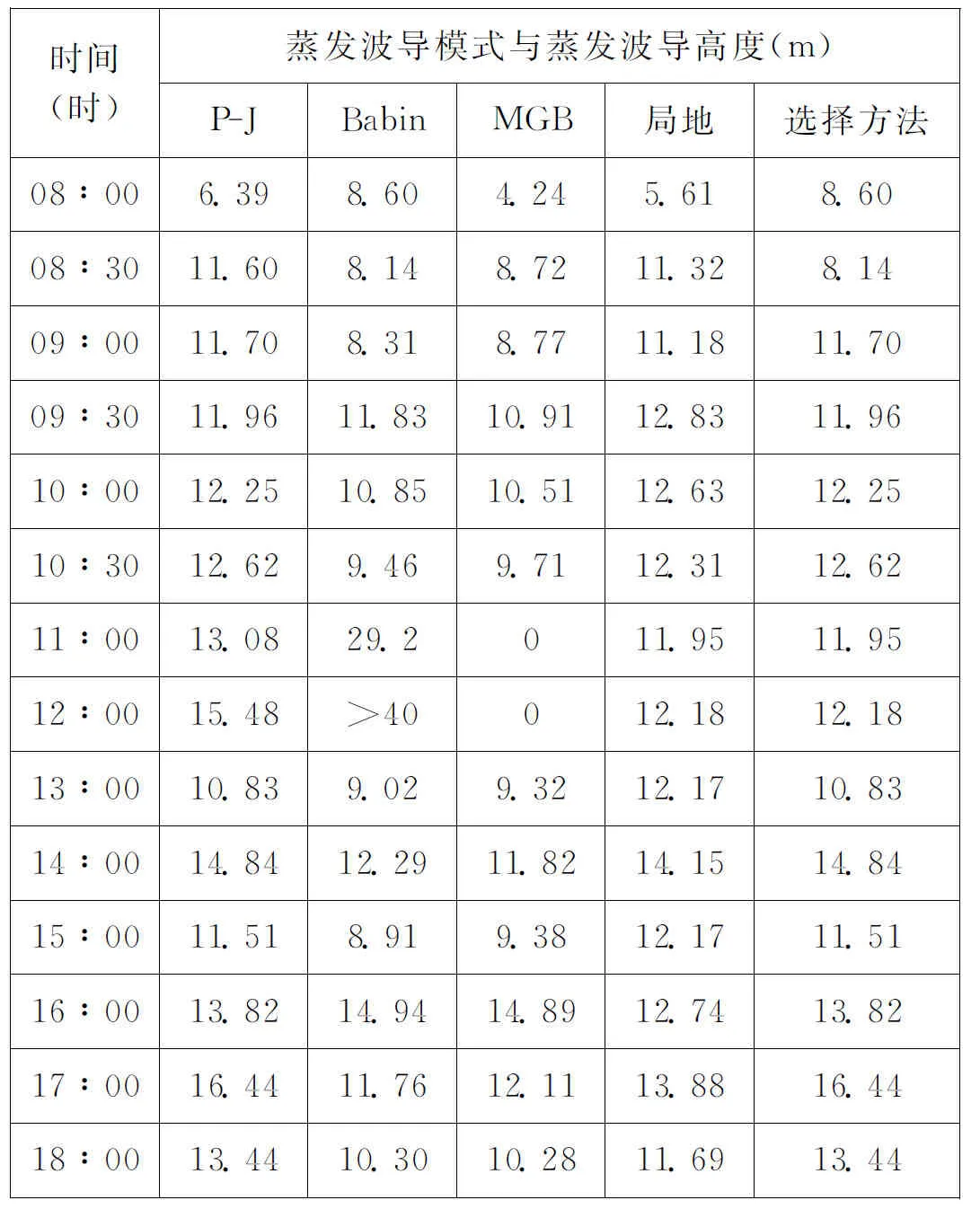
表2　各模型不同时刻预测蒸发波导高度值

利用各预测模式实际预测的波导高度如表2和图1所示。可以看出，在08∶00时刻，海面气海温差小于0，处于不稳定层结海洋大气环境下，且风速较小。除Babin模式外，其他模式给出的波导高度明显偏低，进一步验证了Babin模式在低风速气象环境下的优越性。此时，本文提出的选择方法与Babin模式相同。与其他时刻相比，在11∶00和12∶00时刻各模型给出的蒸发波导高度差异较大，Babin模式给出的高度明显偏高，而MGB模式明显偏低，本文方法与局地相似蒸发波导模式相同，且与P-J模式相接近。在这2个时刻，气温显著高于海面水温，处于强稳定层结海洋大气环境，验证了在强稳定层结海洋大气环境时Monin-Obukhov相似理论不再适用，以该理论为基础的预测模型无法准确预测出波导高度。

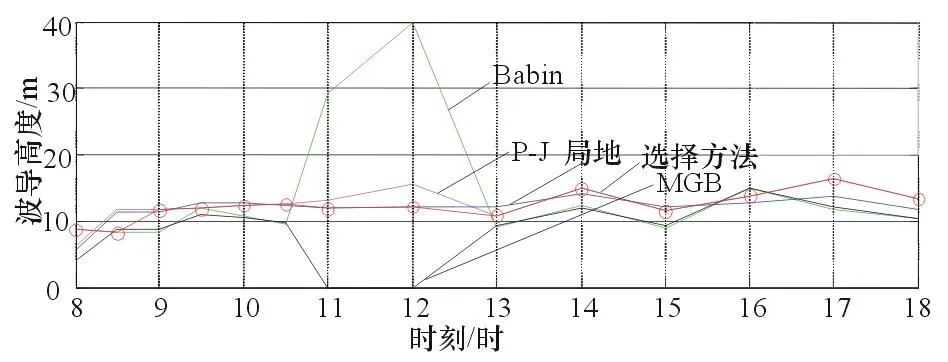
图1　蒸发波导高度

P-J模式预测结果较为接近，是由于该模式在强稳定层结条件下做了人为修正，而基于局地相似理论的蒸发波导模式没有任何修正，因此，认为在强稳定层结海洋大气环境时基于局地相似理论的蒸发波导模式可以更准确地预测得到波导高度。除上述时刻其他时间外，各模式预测得到的波导高度大致相同，且变化趋势相同。本文提出的选择方法与P-J模式相同，主要考虑P-J模式作为成功应用的先例，计算得到的蒸发波导高度较为平缓，稳定性较好。综上所述，本文提出的海上舰艇预测蒸发波导模型选择方法，从理论研究到实验数据的对比分析表明是一种较好的蒸发波导预测模型选取方法。

3结束语

在基于水文气象条件的方法中，本章对现有的典型方法进行了介绍，并对他们的敏感性、稳定性、适应性以及自身的优缺点进行了详细的比较分析，提出了海上舰艇预测蒸发波导模型选择方法，从理论研究到实验数据的对比分析表明该方法具有明显的优势。

参考文献

[1]Jeske H.The state of radar-range prediction over sea[A].Part Ⅱ,AGARD-CP-70[C],1971:1-10.

[2]Paulus Richard A.Specification for evaporation duct height calculations[J].Naval Ocean Systems Center,1989(4):139-148.

[3]Lue Musson-Genon,Sylvie Gauthier,Eric Bruth.A simple method to determine evaporation duet height in the sea surface boundary layer[J].Radio Science,1992,27(5):635-644.

[4]Babin Steven M,Young George S,Carton James A.A new model of the oceanic evaporation duct[J].Journal of Applied Meteorology,1997,36(3):193-204.

[5]刘成国,黄际英,江长荫,等.伪折射率和相似理论计算海上蒸发波导剖面[J].电子学报,2001,29(7):970- 972.

[6]李云波,张永刚,唐海川,等.基于海气通量算法的海上蒸发波导诊断模型[J].应用气象学报,2009,20(5):628-633.

[7]戴福山,李群,董双林,等.大气波导及其军事应用[M].北京:解放军出版社,2002.

[8]成印河,赵振维,何宜军,等.大气波导过程数值模拟研究[J].电波科学学报,2009,24(2):259-264.

[9]李梁, 张海勇,阚荣才.Monin-Obukhov理论在蒸发波导PJ模式中的应用[J].现代防御技术,2014(2):89- 94.

[10]漆随平,王东明,郭颜萍,等.海上蒸发波导的预测方法综述[J].海洋通报,2012,31(3):347-353.

[11]缪刚.海上宽带超视距蒸发波导微波通信系统的建模与分析[J].硅谷,2012(6):188-189.

[12]李诗明,陈陟,乔然,等.海上蒸发波导模式研究进展及面临的问题[J].海洋预报,2005,22(S0):128-138.

[13]王向敏.海上大气波导的预测方法[D].南京：南京信息工程大学,2007.

[14]宋伟,田斌,周沫,等.蒸发波导预测模型研究[J].华中科技大学学报(自然科学版),2013,41(5):52-56.

[15]郭相明,康士峰,张玉生,等.蒸发波导模型特征及其适用性研究[J].海洋预报,2013,30(5):75-83.

Prediction Model Selection Method of Maritime Evaporation Wave-guide

ZHOU Peng，LIU Guang-hui

(Unit 91404 of PLA,Qinhuangdao 066001,China)

Abstract:The prediction method of evaporation wave-guide based on hydrological meteorological condition is a common method.This paper presents the prediction model selection method of maritime ship evaporation wave-guide based on detailed comparison and analysis of existing typical methods from sensitivity,stability,adaptability and advantage/disadvantage.The comparison and analysis of theoretical study and experimental data show that the method has obvious advantages,which is of important meaning to raise the prediction ability of maritime evaporation wave-guide.

Key words:evaporation wave-guide;predication model;selection method

收稿日期:2015-04-08

DOI:10.16426/j.cnki.jcdzdk.2015.05.011

中图分类号：TN928

文献标识码：A

文章编号：CN32-1413(2015)05-0046-06