基于云理论的战术数据链效能评估

陈　槟，尹亚兰，万　福

(海军指挥学院,南京 211800)



基于云理论的战术数据链效能评估

陈槟，尹亚兰，万福

(海军指挥学院,南京 211800)

摘要：战术数据链的指标体系中不仅包含可进行实测的定量指标，还有一部分不可量化的定性指标。针对该特点，提出用云理论解决其效能评估的问题,建立评估的指标体系，并将各指标用云模型表示，研究云理论评估的方法，在云重心加权偏离度的计算中，可能有某些指标对偏离度的贡献与实际意义正好相反，因此对云重心归一化公式进行修正。最后通过实例计算证明了修正后的方法评估可信度更高。

关键词：战术数据链；效能评估；云理论；云重心；加权偏离度

0引言

战术数据链是将广域分布的数字化指挥中心、指挥所、参战部队和武器平台链接起来的信息处理、交换和分发系统。它就像“战争巨人”的神经系统，使得单独的、孤立的武器单元联结起来，形成巨大的战争网络[1]，最大限度发挥武器系统的火力优势。目前对战术数据链的效能评估也多为在数据链应用下的火力优势评估，即从作战效果上来评价战术数据链的优劣，而且大部分的效能评估往往只考虑战术数据链本身的性能，而忽略了其中人为因素的影响。实际上，在战术数据链作战运用过程中，其效能的充分发挥离不开作战指挥人员及战术数据链操作人员的优良表现。加入这些人为因素的影响，显然会使综合评价的结果更加准确可信。在指标体系中，人为因素的影响往往不可精确度量，被称为定性指标，常用“好”、“很好”等语言值对这些定性指标的优劣进行描述。

人为因素的加入使指标体系中定性指标的比重增加，给评估带来一定难度，传统的灰色理论法、模糊综合评判法、层次分析法(AHP)等都无法对定性定量指标共存的综合指标体系进行客观精准的评估。这时云理论就体现了其优势：可将模糊性和随机性有机结合在一起，充分实现精确数值和定性语言之间的转换[2-3]。 因此考虑采用云理论来解决战术数据链效能评估问题。

1战术数据链指标体系研究

1.1　指标体系建立

战场态势瞬息万变的信息化战争下，对通信系统的基本要求包括：有效、迅速、可靠[4]。战术数据链作为一种对作战进行全面保障的特殊通信系统，其基本要求也可归纳为有效、迅速、可靠3点。再根据指标体系建立的客观、完整、科学等原则，可建立如图1所示的指标体系。

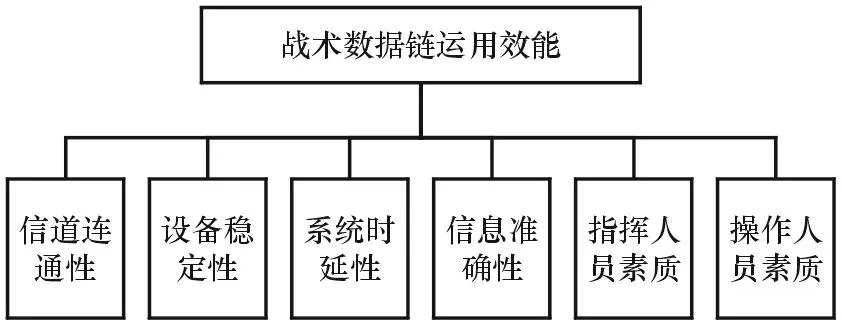
图1　战术数据链运用效能指标体系

1.2　指标分析

信道连通性是指战术数据链网络中各节点间信道正常连通的概率，该值与不同的信道选择以及通信距离有关。

设备稳定性指战术数据链装备正常工作时间在总作战时间中所占的比例。遂行作战任务时，数据链装备只有正常工作和故障2种状态，一旦发生故障，维修人员就对故障进行检修，维修人员素质高低直接影响故障时间的长短，从而影响指标值大小。

信息传输时延包括信源编码时间、发送等待时间、编码调整时间、数据发送时间、数据接收时间、数据处理时间等,主要由有数据链装备的硬件性能、传输数据的类型、数据量大小、传输距离等决定。

战术数据链的数据准确性常用误码率来衡量，即单位时间内数据链系统接收的错误码元数和总码元数的比值。该指标也反映了战术数据链系统的抗干扰能力。影响数据准确性的因素有原始数据误差、敌方蓄意干扰、噪声干扰、信息速率、装备纠错与融合能力等。

战术数据链指挥人员主要负责数据链网络的规划、战术任务的分配，并与各参战部队进行协调，确保战术任务的有效执行。

战术数据链操作人员素质包括能否承受强大的心理压力，能否在错综复杂的信息中分析处理各种不同类型的信息，能否坚持连续作业，能否集中精力，能否不误操作导致死机、中断等严重后果[5]等。

2基于云理论的战术数据链效能评估方法研究

2.1　云理论的基本概念

云理论是定性概念与其定量表示之间不确定性转化的理论[6-7]。设U是一个有精确范围的论域，论域中任意元素x，都对某一定性概念A有着一定的倾向，倾向值y=μA(x),表示x对概念A的确定程度，x在论域上的分布称为云模型，简称云。

云的数字特征可用期望Ex、熵En和超熵He来表示[8]，它们反应了定性概念A的定量特征。

期望值Ex是定性概念在论域中的中心值，也就是最能代表这个定性概念的量化值。

熵En是定性概念的不确定性反应，有3个方面的表现：一是反映了论域中可被定性概念A接受的云滴群的范围大小，即模糊度，是定性概念亦此亦彼性的度量；第二还反映了在论域中云滴群能够代表这个语言值的概率密度，表示代表定性概念的云滴出现的随机性；最后，熵还揭示了模糊性和随机性的内在关系，可以用来代表一个定性概念的粒度。

超熵He是熵的不确定性的度量，即熵的熵，反映了云滴的离散程度。超熵是由熵的随机性和模糊性决定的，超熵越大，云滴的离散度越大，云的“厚度”也越大。

云重心可以表示为T=a×b，a表示云重心的位置，b表示云重心的高度。期望值反映相应的模糊概念的信息中心值，即可作为云重心位置。当期望值发生变化时，它所代表的信息中心值发生变化,云重心的位置也相应地改变。期望值相同的云可通过比较云重心高度的不同区分它们的重要性，即云重心高度反映了云的重要程度。所以说，通过云重心的变化情况可反映出系统状态信息的变化情况。

2.2　基于云理论的战术数据链效能评估方法研究

要进行战术数据链的效能评估，首先肯定是建立其效能评估的指标体系，并研究各指标所占的权重。本文用AHP法确定权重。

在指标体系中，既有用精确数值表示的定量指标，又有用语言值描述的定性指标，提取n组实测的样品组成决策矩阵。每个精确数值型表示的指标可用一个云模型来表示，其中：

Ex=(Ex1+Ex2+…+Exn)/n

(1)

En=[max(Ex1,Ex2,…,Exn)-

min(Ex1,Ex2,…,Exn)]/6

(2)

同时每个语言值指标可用一个一维综合云模型表示：

Ex=(Ex1En1+Ex2En2+…+

ExnEnn)/(En1+En2+…+Enn)

(3)

En=En1+En2+…+Enn

(4)

这样，用p个云模型就可以表示p个系统指标，那么p个指标所反映的系统状态也就可以用一个p维综合云来表示[9]。当系统状态发生变化时，这个p维综合云的形状也将发生变化，相应的它的重心就会改变。p维综合云的重心用一个p维向量表示，即T=(T1,T2,…,Tp)，其中Ti=ai×bi,i=1,2,…,p。

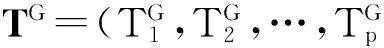
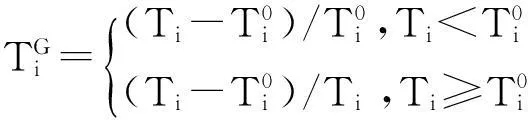
(5)

此时理想状态的云重心向量为(0， 0，…， 0)。因此加权偏离度θ可表示为：

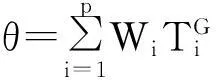
(6)

式中:θ值为负数，其绝对值表示系统状态偏离理想状态的程度，简称偏离程度。

然后构建评语云发生器。采用由11个评语所组成的评语集[10-14]：V=(v1,v2,…,v11)=(vt|t=1,2,…,11)=(无，非常差，很差，较差，差，一般，好，较好，很好，非常好，极好)。

理想状态下系统性能为极好，显然偏离程度越小越好。将11个评语置于连续的语言值标尺上，每个评语都用云模型来实现，比如评语“很好”可用数字特征为(0.8，0.033 3，0.000 1)的云模型来表示，超熵几乎为0，可使图像更清楚直观，也不影响评估精度。其他评语只有期望值的不同，构成一个定性评测语言的云发生器，如图2所示。

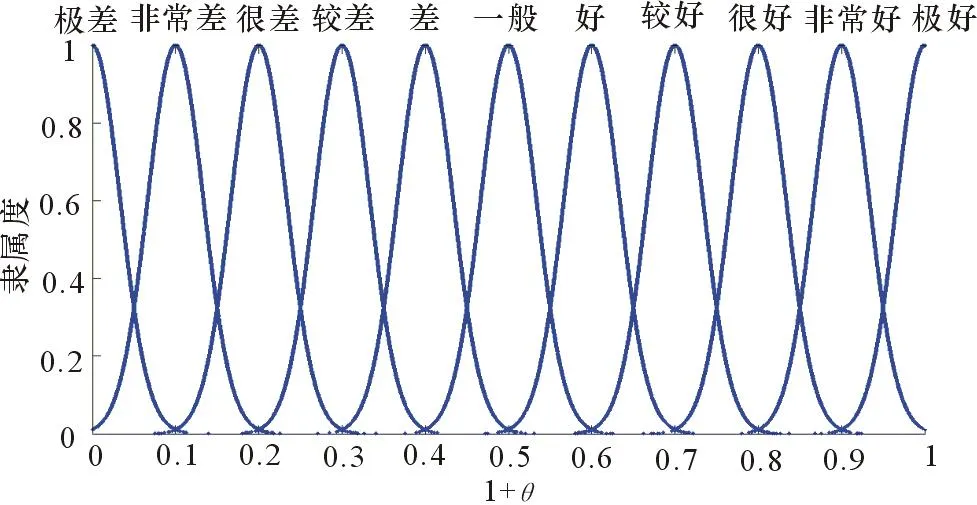
图2　评测云发生器

最后将θ输入评测云发生器中，它可能有以下2种激活情况：

(1) 激活某个评语云模型的程度远大于其它评语(当二者的激活程度的差值的绝对值大于某个给定的阈值)，这时该评语值即可作为对方案的评测结果输出;

(2) 激活了2个评语值的云对象，且激活程度相差很小(当二者的激活程度的差值的绝对值小于某个给定的阈值)，这时运用云理论中综合云的原理，生成一个新的云对象，它的期望值对应的定性表述可由专家或系统用户另外给出。

3对云重心加权偏离度计算的改进

研究第1节中建立的战术数据链效能评估的指标体系，发现一些指标是越大越好，可称为效益型指标，而另一些则是越小越好，为成本型指标。若用式(5)进行统一处理，则2类指标在均为欠理想状态时对偏离程度产生的作用是相反的(效益型指标增大偏离程度，成本型指标缩小偏离程度)，显然不合逻辑。比如信息传输时延是一个成本型指标，追求尽量小，而其他指标都是效益型指标，显然原式仅仅考虑对效益型指标进行归一化，不能直接用于该指标体系的评估。另外，若指挥员思路清晰、组网科学，操作人员技术娴熟、操作熟练，信道传播条件也异常良好，可能会导致实际时延比理想时延还要小。根据式(5)的计算，实际时延比理想时延小得越多。偏离程度越大，将激发评语云发生器中越不理想的评语。而实际上，时延越小评语值应该是越优。 因此，原式并不能客观真实地反应指标的云重心偏离程度，有必要分情况进行讨论：

(1) 对于效益型指标，式(5)可不作修改；

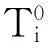
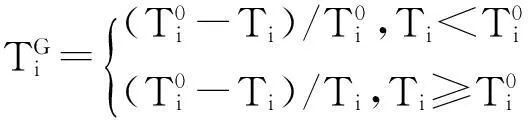
(7)

4战术数据链效能评估算例

图3　各指标权重分布图

首先，针对第1节已建立的指标体系，用AHP法研究各指标的权重。通过咨询专家意见，对信道连通性、设备稳定性、信息传输时延、数据准确性、指挥人员素质、操作人员素质这6个指标构造重要性判断矩阵如下：

将层次模型及判断矩阵输入yaahp软件，得到图3所示的权重分布。权重向量W=(0.302 5,0.081 6,0.240 1,0.091 6,0.166 5,0.117 7)，其中一致性值RC=0.020 8<0.1，表明该判断矩阵有效，权重计算结果可信。

然后，通过演习、计算机模拟等途径，结合专家打分，获取5组指标性能的样本数据，如表1所示。

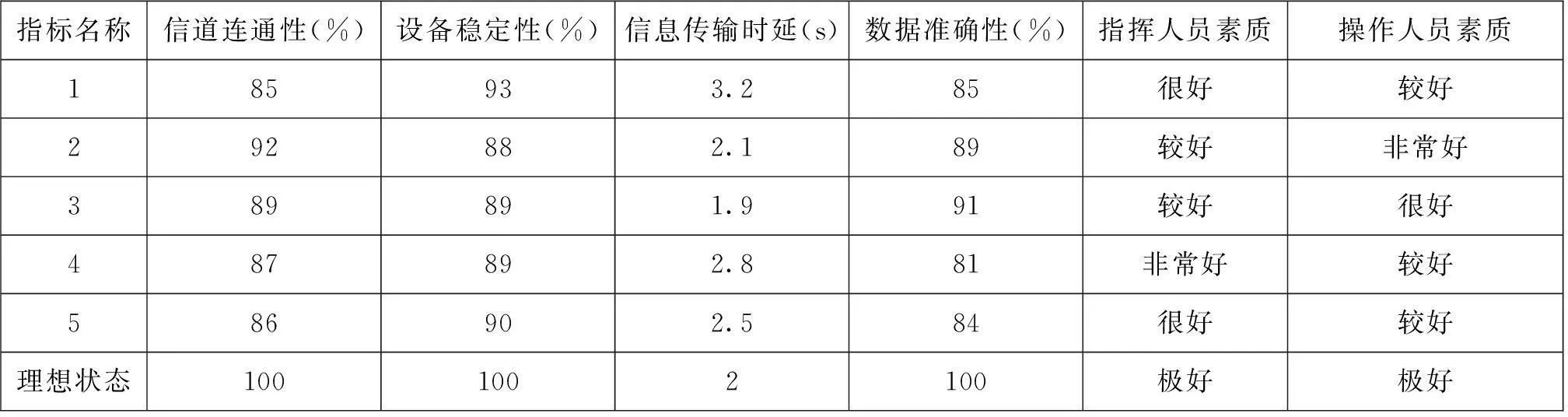
表1　指标性能样本数据

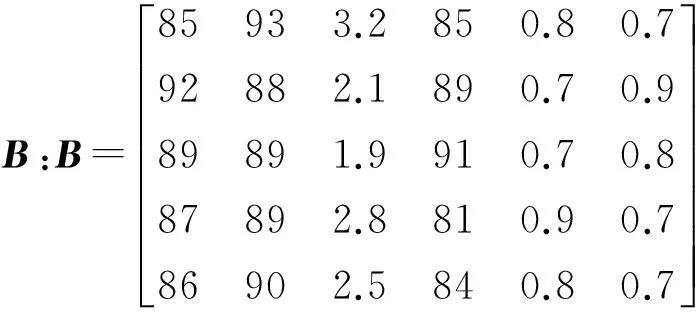
根据云理论，由T=a×b可求得各指标的云重心向量和理想状态的云重心向量：

T=(26.559 5, 7.327 7, 0.600 3, 7.877 6, 0.129 9, 0.089 5)

T0=(30.25, 8.16, 0.480 2, 9.16, 0.166 5, 0.117 7)

根据修正的归一化公式分不同类型指标进行计算，其中信息传输时延是成本型指标，可得到：

TG=(-0.122, -0.102, -0.2, -0.14, -0.22, - 0.24)

表2　各指标云模型的期望值和熵

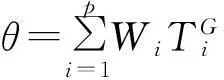
5结束语

战术数据链效能评估指标体系中定性定量指标共存，利用云理论将不同类型指标都用云模型表示，再根据云重心的变化来进行评估，可操作性强。在对综合云重心向量进行归一化时，考虑效益型指标和成本型指标的区别，对归一化公式进行修正，克服了传统方法的局限性，提高了评估的科学性、客观性。评估结果以语言值输出，具有一定的直观性。

参考文献

[1]施荣.国外网络化作战及其关键技术的进展[J].中国电子科学研究院学报，2007,16(2):206-210.

[2]李德毅，孟海军，史雪梅.隶属云和隶属云发生器[J].计算机研究与发展，1995,32(6):15-20.

[3]李德毅.从隶属函数到隶属云[J].计算机研究与发展，1996,9(7):13-18.

[4]SaatyTL.TheAnalyticHierarchyProcess[M].NewYork:McGrawHill,1980.

[5]李有才，郑春弟，黄强.数据链信息系统稳定性影响因素及效能分析[J].舰船电子对抗，2013,36(2):88- 91.

[6]李毅德，刘常昱.论正态云模型的普适性[J].中国工程科学，2004,6(8):28-32.

[7]刘常昱，李毅德，潘莉莉.基于云模型的不确定性知识表示[J].计算机工程与应用，2004,21(2):32-35.

[8]刘常昱，李毅德.正态云模型的统计分析[J].信息与控制，2005,34(2):236-239.

[9]李广强，张兵，王健.基于云重心评判法的雷达模拟训练系统效能评估[J].舰船电子对抗，2009,32(4):105- 108.

[10]焦利明，于伟.基于云重心评判法的指挥自动化系统效能评估[J].情报控制系统与仿真技术，2005,27(5): 71-74.

[11]焦利明，于伟.云重心评判法的防空兵C4ISR系统生存能力效能评估[J].火力与指挥控制，2000,32(5):102- 105.

[12]罗佳，薛青，张国辉，夏永春.基于云理论的C4ISR系统作战效能评估应用与研究[J].系统仿真学报，2012,24(1):212-215.

[13]张目，周宗放.云重心评判法在防空兵作战能力评估中的应用[J].计算机测量与控制，2010,18(8):1928- 1930.

[14]沈进昌，杜树新.基于云模型的模糊综合评价方法及应用[J].模糊系统与数学，2012,26(6):115-122.

Effectiveness Evaluation of Tactical Data Link Based on Cloud Theory

CHEN Bin，YIN Ya-lan，WAN Fu

(Navy Command College,Nanjing 21180,China)

Abstract:The index system of tactical data link includes not only the quantitative index which can be measured practically,but also some qualitative indexes which can't be quantified.For these characteristics,this paper puts forward the method to use the cloud theory to solve the problem of effectiveness evaluation,establish the index system of evaluation,and uses cloud model to represent each index,studies the method of cloud theory evaluation.In the course calculating the weighted deviation degree of cloud center of gravity,there may be some indexes contrary to the practical meanings in the contribution to deviation degree,so the normalization formula of cloud center of gravity need to be modified.Finally,the practical example calculation proves that the modified evaluation method has better credibility.

Key words:tactical data link;effectiveness evaluation;cloud theory;cloud center of gravity;weighted deviation degree

收稿日期:2015-05-27

DOI:10.16426/j.cnki.jcdzdk.2015.05.014

中图分类号：TN914

文献标识码：A

文章编号：CN32-1413(2015)05-0063-05