大悬臂展翅预应力混凝土宽箱梁桥极限承载力分析

余晓琳，贾布裕，杨铮，颜全胜

(华南理工大学 土木与交通学院，广东 广州 510640)



大悬臂展翅预应力混凝土宽箱梁桥极限承载力分析

余晓琳，贾布裕，杨铮，颜全胜

(华南理工大学 土木与交通学院，广东 广州 510640)

摘要:针对大悬臂展翅结构的极限承载能力问题，以某大悬臂展翅预应力混凝土宽箱梁桥为实际工程背景，建立精细的空间有限元模型进行数值分析。考虑结构几何非线性和材料非线性，研究偏心集中荷载、对称集中荷载、均布荷载3种工况作用下，结构的极限承载能力及裂缝的分布规律。结果表明，对称加载形式的极限承载能力大于非对称加载形式的极限承载能力；非对称荷载作用下，桥梁应力及裂缝分布也具有较大非对称性，且悬臂板根部更加容易出现裂缝, 均布荷载作用下，桥梁边跨应力状况劣于中跨。

关键词：极限承载力；大悬臂；展翅箱梁；非线性；裂缝

极限承载力的研究对于结构的设计、施工、运营均有重要意义，国内外学者均有较多研究，如严圣友[1]对30 m部分预应力混凝土箱梁的极限承载能力进行了试验研究，得到结构极限承载力及裂缝分布规律；余波等[2]对左家堡大桥进行了破坏试验，将测点应力和裂缝分布与有限元计算结果进行对比，吻合较好；叶见曙等[3]利用实体退化壳单元研究预应力混凝土多T梁桥的极限承载力；潘家英[4]结合分层有限单元法和UL列式法对大跨度桥梁几何与材料非线性进行耦合分析，并用跨度800 m铁路悬索桥方案极限承载力分析证明；Miller等[5]对挪威Smestua桥进行破坏性试验，最终桥梁受剪破坏，试验说明几何外形和边界条件对桥梁的受力性能有很大影响；Paul等[6]利用足尺模型对I-295公路桥梁进行破坏性试验，结果表明该桥的极限承载能力大于设计值；王凌波等[7]对预应力混凝土箱梁桥开裂后的残余承载力进行了研究，提出承载能力折减系数计算方法来体现开裂后结构的刚度变化[7]；刘会颖等[8]研究了主筋锈蚀对钢筋混凝土梁承载力的影响，得出随受力筋锈蚀率的增大，其极限承载力降低，延性下降。大悬臂展翅宽箱梁桥由于其桥下空间利用率高等优点，近来受到工程界的青睐，但由于其结构的空间效应突出，受力性能非常复杂[9-10]，应用时间较短，目前对其结构极限承载能力的研究较少，若采用模型试验研究则需要耗费巨大的人力物力，而且对于新建成的桥梁，采用实桥进行破坏试验更是不可能。鉴于目前数值算法已经比较成熟，利用大型有限元软件，合理设置材料的特性，能够取得合理的计算结果。本文以某大悬臂展翅预应力混凝土宽箱梁桥为工程背景，对大悬臂展翅结构开展了极限承载力的研究。

1工程背景

某桥(4×42 m)采用现浇大悬臂展翅预应力混凝土连续箱梁结构，全幅桥设置双向6车道，标准梁宽33.5 m，两侧悬臂为7.174 m，梁高2.5 m，梁顶宽3.35 m，箱梁顶板厚0.25 m，底板宽17.50 m，底板厚0.25 m，利用纵向小纵梁来增强箱梁翼缘的抗扭作用，小纵梁高45 cm，宽80 cm，挑梁间下缘弧形板采用椭圆曲线，全联弧形板曲线线形一致，板厚0.2 m，图1为该桥1/2标准箱梁断面图。

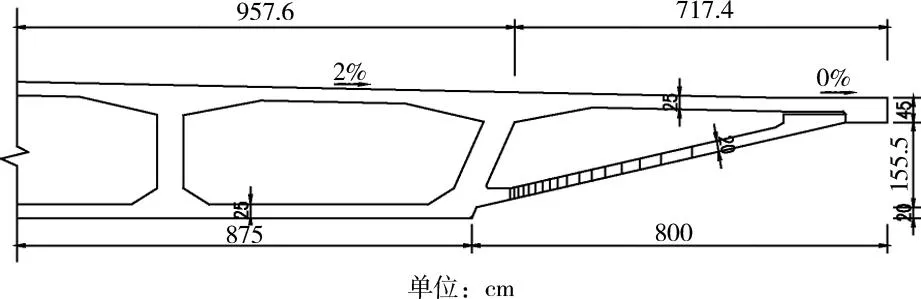
图1　1/2标准箱梁断面图Fig.1 Section of 1/2 standard box girder

2空间数值分析

2.1　模型建立

以4×42 m联为建模对象，利用有限元软件ANSYS建立该桥的空间有限元模型，见图2，SOLID65单元可以模拟混凝土中的加强钢筋以及材料的拉裂和压溃现象，故选用SOLID65单元模拟钢筋混凝土材料，混凝土弹性模量为E=35.5MPa，泊松比为0.2，密度为2 500 kg/m3，混凝土立方体抗压强度标准值为fcu,k=55MPa，单轴抗压强度为fc=25.3MPa，单轴抗拉强度为ft=1.96MPa，闭合裂缝的剪力传递系数为βc=0.95，张开裂缝的剪力传递系数为βt=0.5，拉应力释放系数为Tc=0.6，使用整体式模型考虑普通钢筋的作用，弹性模量为Es=195MPa，泊松比为0.3，密度为7 850 kg/m3，全桥实体模型节点总数为1 434 368个，单元数量为981 666个。

图2　实体模型图Fig.2 Space model of the bridge

由于预应力只是延缓裂缝的开展，并没有提高结构本身的极限承载力，故将预应力钢筋等同于普通钢筋来进行极限承载力分析，预应力的数量按照强度比换算为普通钢筋，然后把所有的普通钢筋以整体式模型进行处理。钢筋的屈服强度fy=300MPa，弹性模量为Es=1.95×105MPa。

2.2　荷载工况

采用以下3种工况加载计算分析其极限承载力，具体加载工况见表1所示，采用逐级加载，直到程序通过破坏准则认定结构已经破坏为止。

集中加载位置如图3所示。

表1　加载工况汇总表

图3　桥梁模型集中加载位置示意图Fig.3 Centralized load position of bridge model

2.3　非线性数值分析

2.3.1几何非线性

对于几何非线性，一般钢筋屈服应变不超过0.001，混凝土压碎应变不超过0.003，故2种材料变形为小应变模式[9]，可以采用T·L列式，即以最初始构形作为参考建立方程，且参考位形保持不变，适用于大位移、小应变几何非线性问题[11]。

2.3.2材料非线性

对于材料非线性问题，需要解决材料的本构关系、屈服准则、强化准则、破坏准则等问题，其中在塑性区范围内用塑性材料的本构关系矩阵De代替原来的弹性系数矩阵D，可得到弹塑性分析有限元平衡方程，混凝土单轴应力应变关系采用式(4)[12]，不考虑下降段使用。

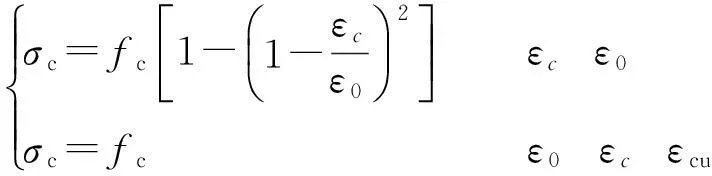
(4)

其中：fc为混凝土单轴抗压强度，取值25.3MPa；ε0为混凝土压应力达到fc时的混凝土压应变，取为0.002；εcu为混凝土极限压应变，取为0.003 3。

对于混凝土和钢筋结构，采用VonMise屈服条件更为合理[13], 对混凝土采用多线性等向强化模型MISO模型，把钢筋材料认为理想弹塑性模型，采用双线性等向强化模型BISO模拟, 破坏准则是SOLID65单元的多参数破坏准则[13]。

2.3.3非线性数值求解

结构非线性有限元分析可以归结为非线性代数方程的求解，ANSYS程序通过使用牛顿-莱布尼茨平衡迭代，迫使在每一个增量的末端解在某个容限范围内达到平衡收敛，最终得到非线性方程解。

3计算结果及分析

由于本桥具有对称性，故分析一半结构就可以得到全桥的规律，而结构边跨端部缺少了纵向弯矩的约束，受力比中跨更为不利 ，本文考虑结构不利状况，只对第四跨进行分析，程序根据设定的步数进行加载和迭代计算，得到图4为工况1第4跨跨中挠度与荷载关系曲线图，图5为工况2第4跨跨中挠度与荷载关系曲线图，图6 为工况3第4跨跨中挠度与荷载关系曲线图，跨中挠度与荷载呈线性关系的阶段为线性阶段，线性阶段末点到结构破坏前为开裂阶段，将即将破坏的一瞬间定义为破坏阶段，可得到结构各工况极限承载力汇总表，见表2。

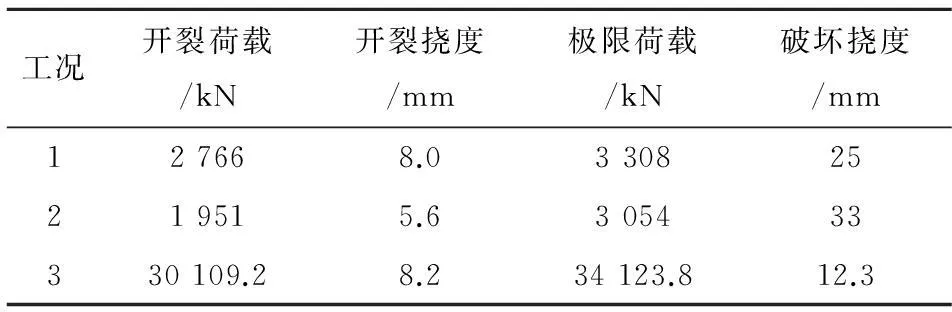
表2　结构各工况极限承载力汇总表

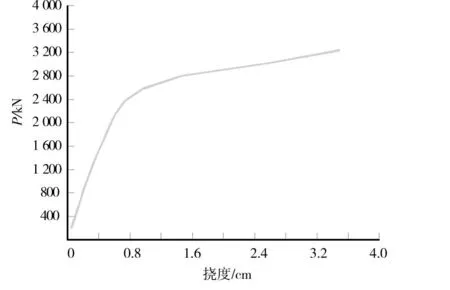
图4　工况1第4跨跨中挠度与荷载关系曲线图Fig.4 Deflection of middle-span and load relationship curve of the fourth span under load case one

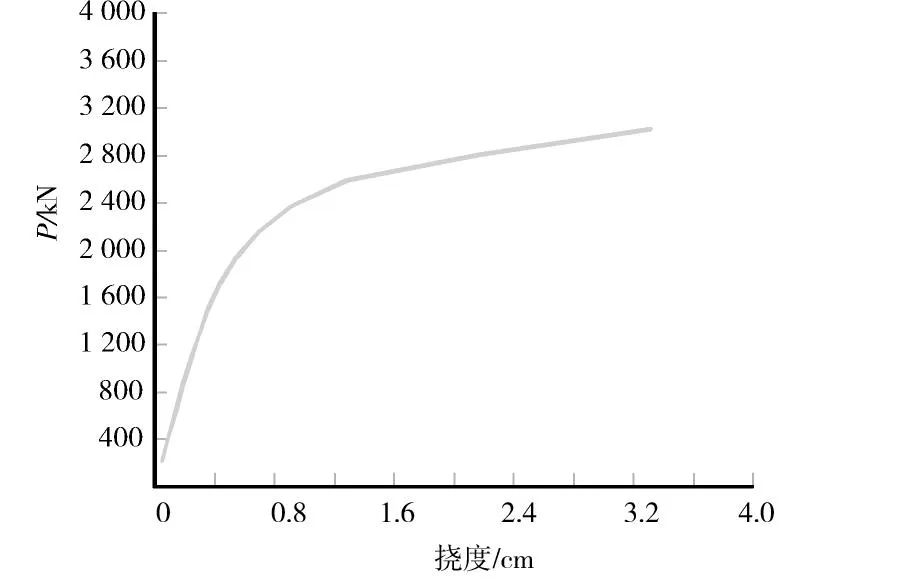
图5　工况2第4跨跨中挠度与荷载关系曲线图Fig.5 Deflection of middle-span and load relationship curve of the fourth span under load case two

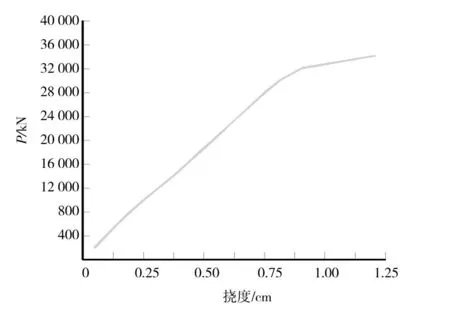
图6　工况3第4跨跨中挠度与荷载关系曲线图Fig.6 Deflection of middle-span and load relationship curve of the fourth span under load case three

3.1　线性阶段分析

在线性阶段，3种工况下均有类似特点，支点顶板纵向受拉，较大值沿横向集中在箱室顶部区域；支点顶板横向受压，在支座对应处有小范围受拉区域；支点底板纵向受压，横向分布均匀，并沿纵向向跨中扩展；支点底板横向受压，在支座支撑对应区域压应力较大；支点底板主应力为压应力，并沿纵向向跨中扩展；跨中顶板纵向受压，并沿横向扩展到翼缘两侧；跨中顶板横向受压，较大值集中在加载附近区域，但在内腹板顶处为拉应力，沿纵向呈狭长条形分布；跨中顶板主应力主要为压应力，但在内腹板顶处附近为拉应力，并沿纵向呈宽条形分布。跨中底板纵向受拉，横向分布不均匀，在加载附近区域出现较大纵向拉应力；跨中底板横向受压为主，在内腹板底区域有较大值，沿纵向呈长条形分布；跨中底板主应力为拉应力，在加载附近区域出现较大主拉应力，在线性阶段，已有小部分裂缝在支点截面处产生，集中在两侧外室底板支撑附近。

3.2　开裂阶段分析

图7为工况1开裂阶段第4跨主应力云图，支点顶板主应力为拉应力，相比线性阶段，拉应力值已有较大增长，尤其在内腹板顶部区域，支点底板纵向受压，在外室腹板底处压应力较大；支点底板横向受压，各室室中区域压应力较大；支点底板主应力为压应力，跨中附近区域：跨中顶板主应力主要为压应力，但在靠近内腹板顶附近处为拉应力，沿纵向呈狭长条形分布，部分较小局域已接近抗拉极限；跨中顶板纵向受压，较大值集中在加载附近区域，相比线性阶段，纵向压应力值已增长数倍，并向周围极限扩散，但并未达到抗压强度值；跨中顶板在加载附近区域有较大横向压应力，但内腹板顶附近有较大拉应力，沿纵向呈长条形分布。跨中底板在中心区域的局部主拉应力已超过最大抗拉强度，底板在该部位发生开裂，中心区域周围的主拉应力大部分已接近抗拉极限；附近区域的纵向应力也已基本接近最大抗拉强度，面临横向开裂；横向应力方面，分布不均匀，在内腹板底部区域有较大的压应力。

图8为工况1开裂阶段第4跨裂缝图，在支点截面处裂缝继续扩展，而在跨中附近底板处则已产生大量裂缝，外腹板底开始开裂，并沿着梁高向上扩展。

图9工况2开裂阶段第4跨主应力云图，支座附近受力与工况1类似，但具有较明显的不对称性，跨中顶板主应力主要为压应力，腹板顶附近出现拉应力，其中在荷载侧内腹板顶附近较大，沿纵向呈狭长条形分布，部分较小局域已接近抗拉极限；跨中顶板纵向受压，较大值集中在加载附近区域，相比线性阶段，纵向压应力值已增长数倍，并向周围极限扩散，但并未达到抗压强度值；跨中顶板横向应力方面，在加载区域以及加载侧外室室中存在较大横向压应力，而在加载侧内腹板附近存在条状横向拉应力，数值较大，部分区域已接近抗拉极限，面临纵向开裂。跨中底板在加载附近区域的局部主拉应力已超过最大抗拉强度，底板在该部位发生开裂，中心区域周围的主拉应力大部分已接近抗拉极限；附近区域的纵向应力也已基本接近最大抗拉强度，面临横向开裂；横向应力方面，开裂区域周围靠近加载侧内腹板底处有小块数值较大的横向压应力，而横向拉应力则呈不均匀的小块状分布。

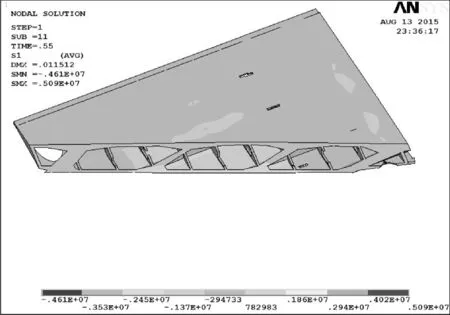
单位：Pa图7　工况1开裂阶段第4跨主应力云图Fig.7 Principal stress nephogram of the fourth span in cracking stage under load case one

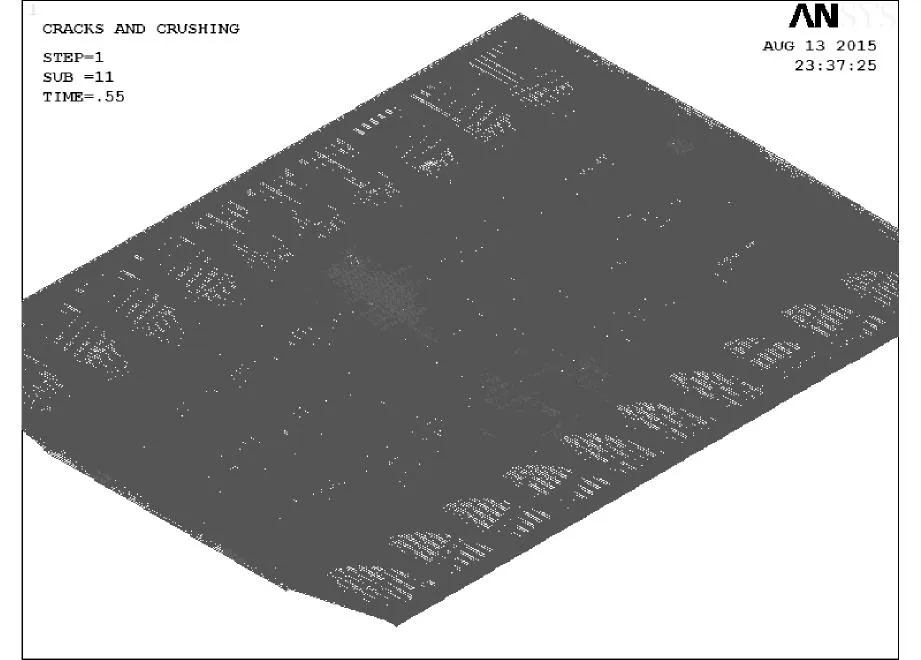
图8　工况1开裂阶段第4跨裂缝图Fig.8 Crack nephogram of the fourth span in cracking stage under load case one

图10工况2开裂阶段第4跨裂缝图，在支点截面处裂缝继续小幅扩展，而在跨中附近加载侧底板和外腹板处则已产生大量裂缝，呈现明显的空间不对称性。

单位：Pa图9　工况2开裂阶段第4跨主应力云图Fig.9 Principal stress nephogram of the fourth span in cracking stage under load case two

图11工况3开裂阶段第4跨主应力云图，支点附近顶板主应力为拉应力，在支座对应区域处值较大，其中边支点支座对应的部分区域主拉应力已超过抗拉极限发生开裂；支点顶板纵向拉应力继续增大，边支点支座对应区域的纵向拉应力已超过极限抗拉强度，周围呈椭圆形区域的纵向拉应力也已接近抗拉强度，中支点支座区域拉应力则比边支点处的小，但同样面临开裂；支点顶板中室区域横向受拉继续增强，各腹板顶处沿纵向的条形分布收窄，在支座对应区域已出现接近抗拉强度的拉应力。支点底板纵向受压继续增强，在边支点和中支点支座区域处值较大；支点底板横向受压，在支座区域处的压应力继续增强，并向周围扩展；支点底板的主压应力分布仍较为均匀；跨中顶板纵向压应力继续增强扩展，外边跨跨中区域的纵向压应力仍比内边跨跨中区域大；跨中顶板横向应力方面，各腹板顶处的拉应力值大幅减小；跨中顶板主压应力范围继续扩大。外边跨跨中底板部分区域的的主拉应力已超过抗拉强度发生开裂，而内边跨跨中底板区域的主拉应力也已大幅上升，接近混凝土抗拉强度。跨中底板纵向受拉继续增强，其中外边跨跨中区域的纵向拉应力已接近混凝土抗拉强度，且分布区域较大；跨中底板横向受压增大，分布仍较为均匀。

图10　工况2开裂阶段第4跨裂缝图Fig.10 Crack nephogram of the fourth span in cracking stage under load case two

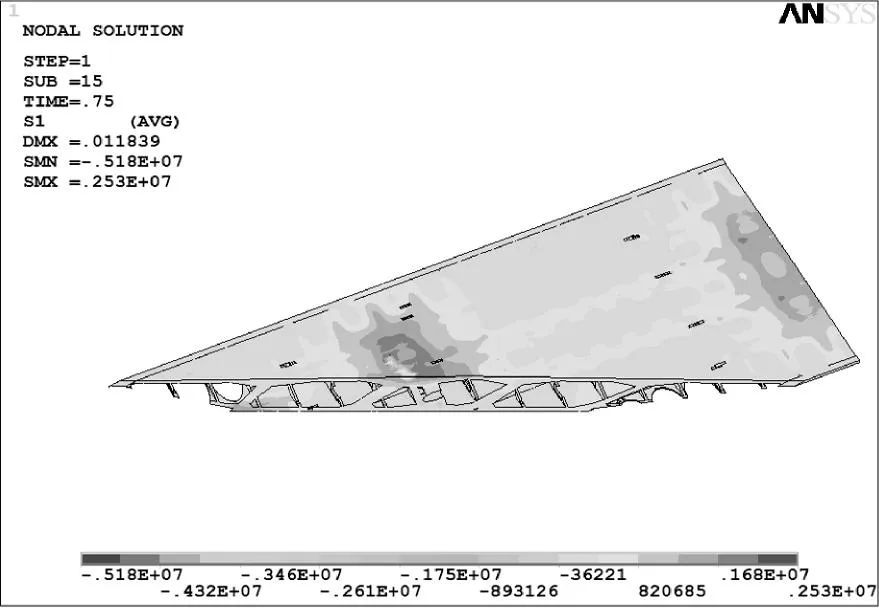
单位：Pa图11　工况3开裂阶段第4跨主应力云图Fig.11 Principal stress nephogram of the fourth span in cracking stage under load case three

图12工况3开裂阶段第4跨裂缝图，已有小部分裂缝在支点截面底板处产生，集中在两侧外室底板支撑附近，同时在外边跨跨中底板区域以及边支座对应的部分区域也有较多的裂缝产生。

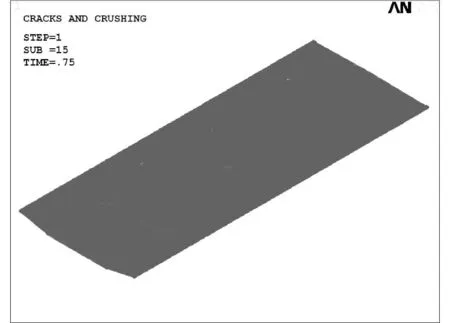
单位：Pa图12　工况3开裂阶段第4跨裂缝图Fig.12 Crack nephogram of the fourth span in cracking stage under load case three

3.3　破坏阶段分析

对于工况1破坏阶段，全跨的底板由于跨中大面积开裂，作用已忽略；跨中附近顶板受到腹板开裂影响，在腹板顶部处受较大主拉应力作用，尤其是内腹板顶部，并沿纵向呈条形分布，在支点顶板附近往跨中侧已有大面积的主拉应力超过抗拉强度发生开裂，周围附近区域的主拉应力也已接近抗拉强度，面临开裂。

图13为工况1第4跨裂缝分布图，在破坏前阶段，跨中附近底板处则已产生大面积密集的裂缝，底板已开裂，其中跨中中心沿横向部分区域经历2次开裂，其中在外室底板的2次裂缝比内室底板的多。在跨中附近区域的腹板已产生沿梁高分布的密集裂缝，并扩展到了顶板底部，值得注意的内腹板沿梁高的裂缝明显比荷载作用处的外腹板的裂缝多，且部分区域经历2次开裂。支点处附近顶板的裂缝集中在支点对应区域，分布面积不大。此时结构已达到破坏临界点，裂缝分布具有明显对称性。

对于工况2，在内支点顶板附近往跨中侧已有大面积的主拉应力超过抗拉强度发生开裂，并向周围区域扩散，周围附近区域的主拉应力也已接近抗拉强度，面临开裂；该区域对应的纵横向有很大的应力；全跨的底板由于跨中大面积开裂，作用已忽略，跨中附近顶板底受到腹板开裂影响，在腹板连接处受主拉应力作用，并已超过抗拉强度发生开裂，由于荷载的作用，荷载则的应力较大，裂缝也较多，值得注意的是在和荷载侧的跨中翼缘顶板底部也有较大的主拉应力而发生开裂，尤其是顶板翼缘侧和横撑支撑相连处，说明外侧横撑发挥着与箱室相似的作用。在荷载作用以及中室顶板顶区域继续承受较大的纵横向压应力，且从荷载侧向非荷载侧扩散。

(a)腹板；(b)顶板；(c)底板图13　工况1第4跨破坏阶段裂缝分布图Fig.13 Crack distribution nephogram of the fourth span in cracking stage under load case one

图14为工况2第4跨破坏阶段裂缝分布图，跨中附近底板处则已产生大面积密集的裂缝，底板已开裂，其中荷载侧对应的底板部分区域经历了两次开裂，值得注意的是在跨中非荷载侧的底板的裂缝比荷载侧的裂缝多，应和荷载侧开裂后的内力重分配有关。在跨中附近区域的腹板已产生沿梁高分布的密集裂缝，并扩展到了顶板底部，其中荷载侧腹板沿梁高部分区域经历二次开裂。内支点处附近顶板的裂缝并非集中在支点对应区域，而是在往跨中侧延伸长度约有L/4的区域，且分布面积大。此时结构已达到破坏临界点。

工况3在破坏前阶段，跨中附近腹板顶部处受较大主拉应力作用，尤其是内腹板顶部，并沿纵向呈条形分布，在边支点顶板附近已有大面积的主拉应力超过抗拉强度发生开裂，周围附近区域的主拉应力也已接近抗拉强度，面临开裂，同时中支点顶板附近区域的主拉应力也已接近抗拉强度面临开裂；在边支点和中支点顶板区域的纵横向方向均有很大的拉应力。外边跨跨中底板已大面积开裂，内边跨跨中底板应力未到临界值，也尚未有裂缝。

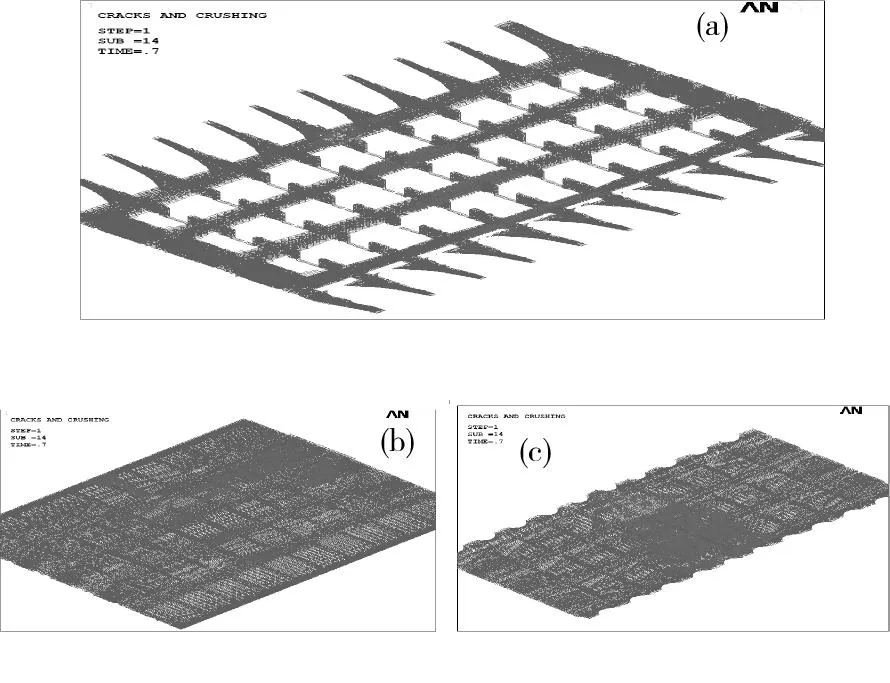
(a)腹板；(b)顶板；(c)底板图14　工况2第4跨破坏阶段裂缝分布图Fig.14 Crack distribution nephogram of the fourth span in cracking stage under load case two

图15为工况3第3和4跨裂缝分布图，在破坏阶段，外边跨跨中附近底板处则已产生大面积密集的裂缝，底板已开裂。在跨中附近区域的腹板已产生沿梁高分布的密集裂缝，但尚未扩展到顶板底部。边支点处附近顶板已有大面积裂缝产生，并扩展到了腹板顶部区域。此时内边跨尚未有裂缝产生，而外边跨已达到破坏临界点。

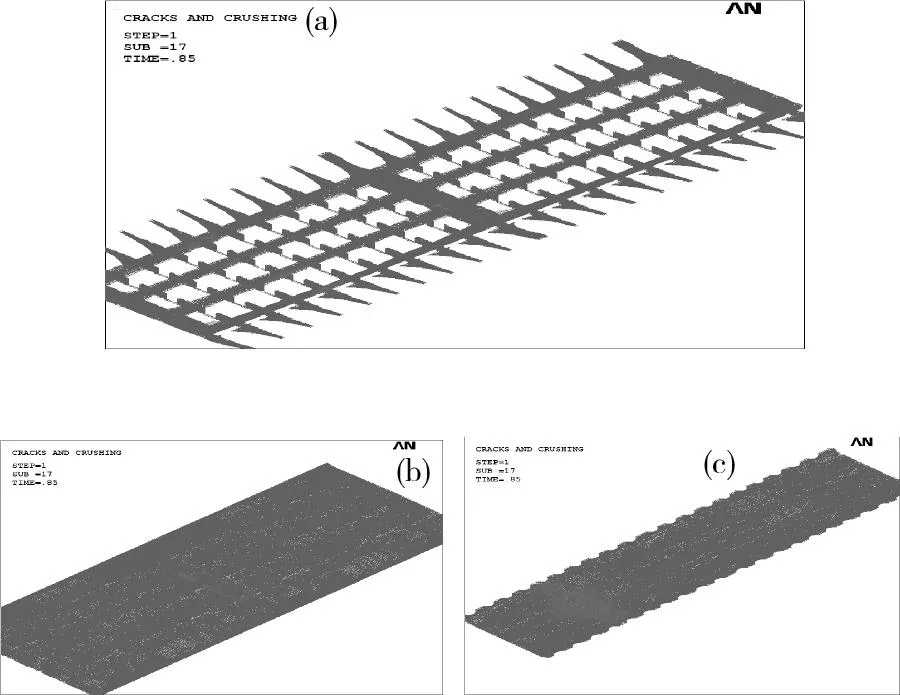
(a)腹板；(b)顶板；(c)底板图15　工况3第3和4跨破坏阶段裂缝分布图Fig.15 Crack distribution nephogram of the third and the fourth span in cracking stage under load case three

4结论

1)对称加载形式的极限承载能力大于非对称加载形式的极限承载能力，全桥均布荷载作用下，桥梁延性较差，破坏时跨中挠度仅仅比开裂时大4.1 mm。

2)非对称荷载作用下，桥梁应力及裂缝分布也具有较大非对称性，且悬臂板根部更加容易出现裂缝，在破坏阶段，由于应力重分布的影响，非荷载侧底板裂缝反而更多。

3)荷载作用下，桥梁的裂缝发展规律类似，先是线性阶段支座处出现裂缝，接着在开裂阶段，跨中底板出现较多裂缝，并往腹板蔓延，在支点截面处裂缝继续小幅扩展，最后在破坏阶段，跨中底腹板大范围开裂，基本可以忽略跨中底板的强度作用，受此影响，跨中顶板主应力由压应力变为拉应力，并开始开裂。

4)在全桥均布荷载作用下，外跨受力状况明显差于内跨，当外跨破坏时，内跨尚未有裂缝产生。

参考文献：

[1] 严圣友.30 m部分预应力混凝土箱梁极限承载能力试验研究[J].公路工程，2012，37(1):87-90.

YAN Shengyou.The test study of the ultimate bearing capacity for the 30 m ppc box girder[J].Highway Engineering, 2012,37(1):87-90.

[2] 余波,李勇,孙晓红,等.左家堡大桥实桥承载力破坏试验及分析[J].公路交通科技，2011，28(7):100-112.

YU Bo, LI Yong, SUN Xiaohong, et al.Destructive test and analysis of bearing capacity of Zuojiabao Bridge[J].Journal of Highway and Transportation Research and Development, 2011,28(7):100-112.

[3] 叶见曙, 张剑, 黄剑峰.预应力混凝土多T梁桥的极限承载力[J].东南大学学报(自然科学版)，2009，39(1):106-111.

YE Jianshu, ZHANG Jian, HUANG Jianfeng.Analysis of ultimate loads of prestressed concrete multi-T girder bridge[J].Journal of Southeast University(Natural Science Edition), 2009，39(1):106-111.

[4] 潘家英,张国政,程庆国.大跨度桥梁极限承载力的几何与材料非线性耦合分析[J].土木工程学报,2000,33(1):5-8.

PAN Jiaying, ZHANG Guozheng, CHENG Qingguo.Geometrical and material nonlinear analysis for determining ultimate load capacity of long-span bridge[J].China Civil Engineering Journal, 2000, 33(1): 5-8.

[5] Miller R A, Aktan A E, Shahrooz B-M.Destructive testing of decommissioned concrete slab bridge[J].Journal of Structural Engineering, 1994,120(7)：2176-2198.

[6] Roschke Paul N, Pruski Kevin R.Overload and ultimate load behavior of posttensioned.slab bridge[J].Journal of Bridge Engineering, 2000,5(2)：148-155.

[7] 王凌波，赵煜.预应力混凝土箱梁桥开裂后的残余承载力分析[J].铁道科学与工程学报，2015,12(1):127-131.

WANG Lingbo, ZHAO Yu.Analysis of residual bearing capacity of cracked prestressed concrete continuous box bridges[J].Journal of Railway Science and Engineering, 2015, 12(1): 127-131.

[8] 刘会颖,张家生,孟飞,等.主筋锈蚀对钢筋混凝土梁承载特性的影响[J].铁道科学与工程学报， 2014,11(4): 26-31.

LIU Huiying, ZHANG Jiasheng, MENG Fei, et al.Effects of main bars corrosion on the bearing behavior of reinforced concrete beams[J].Journal of Railway Science and Engineering, 2014,11(4): 26-31.

[9] 华波,朱朝阳,朱安静.大悬臂多腹板宽箱梁受力特性研究[J].交通科技,2012(2):1-3.

HUA Bo, ZHU Chaoyang, ZHU Anjing.Force analysis for broad box girder with long cantilever and multi web[J].Transportation Science & Technology, 2012(2):1-3.

[10] 徐岩.大悬臂展翅箱梁悬臂长度分析[J].三峡大学学报(自然科学版)，2012，34(4):55-58.

XU Yan.Cantilever length analysis of large cantilever wing-box girder[J].Journal of China Three Gorges University(Natural Science), 2012,34(4):55-58.

[11] 李海青，杨万里，高璇.预应力混凝土薄壁高墩刚构桥梁极限承载力分析[J].中国公路学报，2013,26(6)：128-134.

LI Haiqing, YANG Wanli, GAO Xuan.Analysis of ultimate bearing capacity of prestressed concrete frame bridge with high piers[J].China Journal of Highway and Transport, 2013,26(6)：128-134.

[12] JTG D62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

JTG D62—2004, Highway reinforced concrete and prestressed concrete bridges and culverts[S].

[13] 赵敏.大跨径连续刚构桥的极限承载力研究[D].西安:长安大学，2007.

ZHAO Min.The study on ultimate bearing capacity of long-span continuous rigid frame bridge[D].Xi’an: Chang'an University, 2007.

(编辑阳丽霞)

Analysis of ultimate bearing capacity of prestressedconcrete box-girder bridge with large-cantilever-wing

YU Xiaolin，JIA Buyu，YANG Zheng，YAN Quansheng

(School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640, China)

Abstract:To study the ultimate bearing capacity of the large cantilever structure, an accurate space finite element model was built for numerical analysis with the background of a prestressed concrete box-girder bridge with large-cantilevev-wing.Taking into account of the geometric nonlinearity and the material nonlinearity, the structure ultimate bearing capacity and the distribution regularity of cracks under three load cases(eccentric concentrated load, symmetrical concentrated load and uniform distributed load) were analyzed.It is concluded that the structure ultimate bearing capacity under the load case of symmetrical load is larger than that under the case of asymmetrical load; the distributions of the stress and cracks under the load case of asymmetrical load are also asymmetrical and cracks are more likely to appear in the root of the cantilever wing.The stress condition of side span is worse than mid-span under uniformly distributed load.

Key words:ultimate bearing capacity; large-cantilever-wing; box-girder; nonlinear; crack

通讯作者：贾布裕(1983-)，男，浙江义乌人，博士，从事大跨度桥梁结构研究；E-mail:ctjby@scut.edu.cn

基金项目：国家自然科学基金资助项目(51208208)；中央高校基本科研业务费专项资金资助项目(2014ZZ0019)；广东省交通运输厅科技项目(科技-2014-02-013)

收稿日期：2015-10-11

中图分类号：U448.21+5

文献标志码：A

文章编号：1672-7029(2015)06-1379-08