双角平分线双剑合璧

王冬升

波利亚指出：拿一个有意义但不复杂的题目去帮助学生发掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的领域. 在数学教学时，教师往往都为选题而烦恼，而浙教版《义务教育教科书·数学》教材编委精心编写的教材例题、习题一般都有典型性、示范性、迁移性、再生性等特点，它们或渗透了某些数学方法，或体现了某些数学思想，或提供了某些重要结论，意义非同一般. 因此，对它们不能简单地就题论题，而应进行开发、引申与挖掘，揭示其有价值的结论. 这样不仅能得到一批“源于教材，而又高于教材”的好题，疏通知识之间的联系，又能开阔学生的思路，培养学生的创造力，产生触类旁通、举一反三的学习效果. 现拟从教材中采撷一例，解析习题的创新再生.

一、原题重现

浙教版《义务教育教科书·数学》七年级上册第六章“图形的初步知识”第七节作业题B组第5题：

如图1，E是直线AC上一点，EF，EG分别是∠AEB，∠BEC的平分线. 求∠GEF的度数.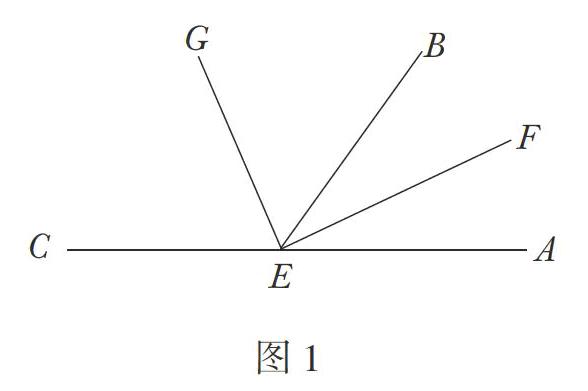

解析：由已知可知：∠GEF=∠CEB+∠AEB=∠AEC=90°.

通过题目的结论我们很容易发现，无论∠AEB和∠BEC如何变化，即当射线EB绕点E旋转时，∠GEF和∠AEC必有如下数量关系：∠GEF=∠AEC. 这样整齐的等式是非常值得我们对其进行更深层次的研究与探讨. 这是七年级平面几何中比较经典的一道习题，它不仅仅是“角的和差”“角的平分线”这些重要概念的应用，还蕴含着非常重要的数学思想——整体思想.笔者在教学过程中对本题进行了适当的拓展，收到了很好的效果.

二、变式延伸

变式1：改变∠AEC的大小，由180°变为90°.

解析：如图2，由已知可知

∠GEF=∠CEB+∠AEB=∠AEC=45°.

此时∠GEF和∠AEC依然有如下数量关系：∠GEF=∠AEC.

如果∠AEC为任意大小的角，我们发现依然有∠GEF=∠AEC这样的关系.通过上面的初步变换，我们得到了一个一般性结论：“如果∠AEC内部有三条射线EG，EB，EF，其中EG平分∠BEC，EF平分∠AEB，那么∠GEF=∠AEC. ”

变式2：将上述结论中“平分”的条件改为“∠GEB=∠BEC，∠BEF= ∠AEB ”

经过此次变换后得到的结论与变式1中的结论类似，故可以进一步得出：“如果∠AEC内部顺次有三条射线EG，EB，EF，其中∠GEB=∠BEC，∠BEF=∠AEB，那么∠GEF=∠AEC”.

变式3：将“EG平分∠BEC ”变为“EG 平分∠AEC”

解析：如图4，由已知可知∠GEF=∠AEC-∠AEB=∠BEC.

虽然角平分线的位置发生了变化，但是解决问题的思想没变，仍是应用整体思想将 ∠GEF转化为∠AEC和∠AEB的关系，与前两次变换异曲同工.

变式4：已知∠GEF=90°，顶点E在直线AC 上，使∠GEF绕点E旋转，当射线EF平分∠AEB时，射线GE所在的直线是否平分∠BEC？

解析：（1）如图5，当射线GE与射线EF在直线AC同侧时，易知射线GE平分∠BEC.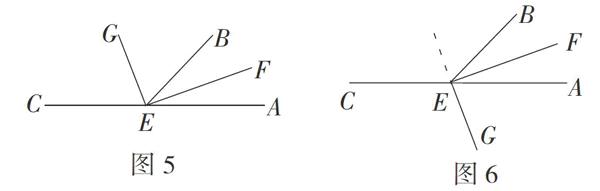

（2）如图6，当射线GE与射线EF在直线 AC异侧时，易知射线GE的反向延长线平分∠BEC .

综上，射线GE所在的直线平分∠BEC.

当一个问题的条件发生变化时，问题结论的形式未必发生变化.对于课后习题的处理不仅仅在于解答的思路与过程，更应该注重挖掘一道习题的典型代表性在什么地方，从而有目的地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，使知识点融会贯通，使思维在所学知识中如鱼得水.

通过对一道课本上的原题进行四种变化，这道教材上的解答题发挥了“以一当四”的作用. 波利亚在《怎样解题》中说过“没有任何一个题目是彻底完成了的”，故我们仍希望通过这道题目得到更多的东西.

回顾前面的变式1、变式2、变式3，我们从改变已知条件上进行变式，其实主要都是围绕射线OB的位置变化情况进行的，所以可以通过如下这样一个题目来对前面三个变式进行总结：∠AEC是小于平角的任意角，作射线EB，再作射线EG，EF， EG平分∠BEC， EF平分∠AEB.当射线EB绕点E旋转时，试探究∠GEF与∠AEC的关系.

通过分析，我们可以发现，这道题目不仅仅是对前面变式的一个总结，在解决问题过程中所应用的数学思想也发生了变化，不仅有整体思想，还增添了分类讨论思想.

在图7、图8中∠GEF与∠AEC的关系是∠GEF=∠AEC.

在图9中∠GEF与∠AEC的关系是 ∠GEF=180°-∠AEC.

对于变式4，可以给出更加丰富的题目背景：

如图10，点O为直线AB上一点，过点 O作射线OC，使∠BOC=120°. 将一直角三角板的直角顶点放在点O处，一边OM在射线 OB上，另一边ON在直线AB的下方.

（1）将图10中的三角板绕点O逆时针旋转至图11，使一边OM在∠BOC的内部，且恰好平分∠BOC. 此时直线ON是否平分∠AOC？请说明理由.

（2）将图10中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，求t的值.

（3）将图10中的三角板绕点O顺时针旋转至图12，使ON在∠AOC的内部，求∠AOM-∠NOC的度数.

例题讲解贵在小而精，以小见大. 教师用在设计例题上的时间与学生做练习的时间是成反比的. 例题设计是否精致，直接决定着学生的学习效果. 在教学中教师要提高对教材中习题的重视程度，对一些具有代表性的好题，不妨小题大做一番！

三、结语

迅速提高解题能力，是教师和学生共同关心的问题之一. 引导学生一题多变，将某些题目适当引申、拓广，不仅可以使学生对知识掌握得更加系统，而且可以激发学生的求知欲望，培养学生数学思维品质以及自觉探究的良好习惯. 通过对课本中典型习题的引申和挖掘，让学生在变化中发现规律，尽量做到能用典型习题这一把“钥匙”开一类“锁”，以达到“做一题，通一类，会一片”的效果.

新课程倡导教师要创造性地使用教材，纵观近几年各地中考试题，有很多题目都源于教材而又高于教材. 因此，在日常教学中教师不要盲目甩开教材，滥用其他资料，搞“题海战术”，而应精心解读教材，站在知识系统的高度用“活”教材. 总之，对于每一道课后习题，都不能“就题论题”，而应该开阔解题思路，通过一题多变、一题多用、多解归一、多题归一等形式，赋予课后习题更多的活力与意义，发掘更多更好的数学模型. 既要重视变化之形，也要重视不变之魂，向学生渗透数学思想和方法，进而获得一种更有力度、充满张力的数学思考，以及触及心灵的精神愉悦.