管窥初中压强表达式建立的教学逻辑

压强作为初中物理的重点章节，其表达式p=的建立方法历来饱受争议[1]. 一般而言，存在着两种主流的学科方法，即比值定义法和控制变量—比例系数法，那么究竟哪种方法更有助于学生对压强概念的掌握呢？鉴于此，我们从认知水平、思维方法、研究范式、教学模式等维度切入，辨析两种方法的适用范围及蕴含的教育功能，希冀为消除压强教学中存在的疑惑有所裨益.

一、表达式的归属：压强表达式建立的症结

中学物理涉及很多表达式，大体可将它们分为两类：一类是定义式，一类是决定式.其中定义式是指利用某几个物理量对一个新的物理量进行定量描述，从中表达出这个新量的物理意义，这个物理量与定义它的量之间一般无比例关系（如a=，C=）；而决定式是利用等式的形式来反映一个新的物理量所受到的制约因素与影响，从这个式子中可以了解新物理量与影响因素间的正、反比例关系（如a=，C=）.一般认为，定义式（尤指比值定义式）是通过比值定义法导出的，决定式则是借助控制变量—比例系数法得到的[2]50. 然而由于压强这一概念是从大学物理中抽取而来，在中学阶段其表达式p=并不算是一个完整的式子. 故而导致初中的压强表达式既带有决定式的性质又具备定义式的特点（如图1所示），这样就造成了压强教学路径的莫衷一是.

二、关于“压强表达式”建立的两种常见教学路径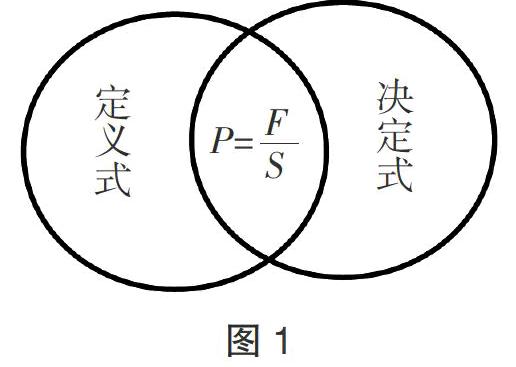

（一）比值定义法的教学逻辑

以力和力的作用效果为教学的逻辑起点，众所周知，力对物体的作用效果或使物体发生形变，或使物体的运动状态改变.于是教师可借此发问：如何比较压力的作用效果呢？回顾之前的知识可知：力对物体的作用有大小之分，由此引导学生提出假设——通过直接比较物体对接触面压力的大小，从而判断它们压力产生的作用效果强弱. 接下来，教师帮助学生设计相关验证实验，如选取两个大小不同的秤砣，将它们置于海绵之上. 结果却显示，重力大的秤砣使海绵形变的程度小，而重力小的秤砣使海绵形变的程度大（物体的重力提供了压力），这与学生平时的日常经验无法契合. 可见直接比较物体压力大小的做法是错误的！由此引发学生的认知冲突，为下一步的教学做出了铺垫. 随后，教师要及时把握教学契机，启发学生找寻谬误产生的根源，并尝试修改先前的假设. 谬误的产生是因为两个秤砣压力作用的面积不一样，即比较时未能选取相同的标准，因此解决问题的方法就是对秤砣的作用面积做标准上的统一.出于简单和方便考虑，我们将借助“除法”这一数学工具，用秤砣产生的压力F除以相应的接触面积S，将选择的标准化为“1平方米”，从而比较“单位面积下秤砣对海绵的作用力”，即以比值的形式进行比较.经计算发现，产生更大作用效果而重力小的秤砣，其比值要更大，正好符合学生的日常生活经验.但这种比较方式却与我们直接比较压力大小的初衷大相径庭，那么究竟这个比值的含义是什么呢？接下来，教师便要为学生解答比值引发的困惑，可从其外延入手，重新回到物理现象中，联系学生的实践经验进行诠释：反映了压力的作用效果，压力越大，受力面积越小，其作用效果就越强，由此我们称比值为“压强”，用字母p表示，有=p.

（二）控制变量—比例系数法的教学逻辑

教师首先以“压力产生的作用效果和哪些因素有关”破题，引发学生的思考，同时通过生活实例来增强学生的感性认识，助其猜想，将他们的注意力聚焦到“物体产生的压力”和“受力面积”两个因素上. 接下来，教师进一步发问，这些因素和压力的作用效果之间存在着怎样的函数关系，我们该如何探究呢？由此帮助学生设计实验，在实验探究过程中，学生会发现这样一个问题：当一个因变量（即压力的作用效果）与两个自变量（物体产生的压力、受力面积）都存在相应的函数关系时，那么该如何“屏蔽”多余的自变量，而仅研究某一个自变量与因变量间的关系呢？此刻，便引出了一种十分重要的方法——控制变量法，即先把几个物理量控制起来，使它们保持不变，从而把研究的问题转化为探究因变量（即压力的作用效果）与单个自变量之间的函数关系，进而总结期间的规律.如保持受力面积一定，让学生观察随物体压力的增减，压力作用效果的变化趋势，从而得出结论：当受力面积相同时，压力越大，压力作用效果越明显，即p∝F；然后再利用此方法得到“当压力相同时，受力面积越小，压力的作用效果越明显”的结论，即p∝；最后把这两条结论组合到一起，便得到“压力的作用效果与压力大小成正比，与接触面积成反比”，用式子表达即为p∝.为把这个比例关系式变为常规意义的等式，应引入一个与压力F，受力面积S均无关的常量k，于是有p=.当力的单位取“牛顿”，面积的单位取“平方米”时，常量k=1，式子被化简为p=.通过解读公式p=可知，压力的作用效果是通过“单位面积上受到压力的大小”来衡量的，这一比值我们称为“压强”，压强与受力面积S、压力F二者有关：受力面积S越大，压强越小；压力F越大，压强越大.

三、两种学科方法的内禀研究

（一）公式内涵解读

物理学是一门大量运用数学语言的科学，绝大部分物理规律都要借助公式和符号进行表达，每一个看似简单的公式抑或符号都蕴含着丰富的物理含义.因此物理教学的一大要务就是让学生学会理解物理符号、运用物理符号，以及识别物理符号背后所传递的信息.以等号“=”为例，其在数学中象征了“等值”的关系，而在其他理科（如：计算机C语言、物理等）还有“赋值”之意，即把“=”右边的值赋给左边.因此，经由两种学科方法得到的压强表达式=p和p=不仅仅是形式上的不同，二者的内涵也是截然不同的，这种不同体现在一种因果的逻辑顺序上.具体而言，=p译为“先得到，后将其赋值为p，即为命名p”；p=则译为“通过探究p的影响因素，得到p与F成正比，与S成反比的结论”.

（二）比较形式与研究范式

毋庸置疑，比值定义法和控制变量—比例系数法的实施都要以比较作为先决条件. 其实，对物体进行比较源自人类对经典物理世界最为朴素、本原的感知. 比较是一切理解和思维的基础. 可以说没有比较就没有认识，就没有研究. 根据时空上的区别，可以把比较分为纵向比较和横向比较. 纵向比较是比较同一对象在不同时期内的发展与变化；横向比较是对同类别的不同对象在相同标准下进行的比较.不难看出，控制变量—比例系数法涉及的比较属于一种比较，因变量和自己的过去做比，即改变自变量大小，观察因变量的变化趋势；而比值定义法涉及的比较则是横行比较，比较同一类事物中的两个对象在某一方面的能力强弱或变化快慢等. 此外，进一步来看，这两种学科方法的背后实际上影射着不同的实验研究范式：控制变量法与单组前后测对应，其实验处理为“使自变量发生变化”；而比值定义法与双组前后测对应，实验处理则是“利用除法统一标准”.两者在比较形式上的不同，最终转变成实验研究范式的迥异.

（三）认知路径与运算水平

认知路径，即人类获取知识的途径. 处于不同认知水平的人，其认知路径是有所差异的. 对此，心理学家西蒙在科学发现规范理论中把认知路径归结为两类：一类是数据驱动，先收集大量数据，然后进行分析，找出规律并予以解释；另一类是概念驱动，先提出假设，然后根据实验来检验并修改假设.有研究显示[2]51，这两种认知路径对应着学生不同的认知水平，数据驱动契合具体运算阶段的认知规律，而概念驱动则契合形式运算阶段的认知规律. 如果能厘清比值定义法和控制变量—比例系数法与这两种认知路径间的对应关系，无疑有助于我们在教学中贯彻因材施教的原则，即结合不同认知水平学生获取知识的特点，合理选择建立物理概念的方法. 那么究竟哪种学科方法属于概念驱动模式，哪种又属于数据驱动模式呢？分析两种学科方法的特点后，我们认为以分析数据，归纳规律入手的控制变量—比例系数法是数据驱动模式；而以提出假设、验证假设入手的比值定义法则是概念驱动模式. 可见，两种学科方法的不同，实际体现了人类认知路径的不同.

（四）教学模式层面

教学模式是指在一定教学思想的引领下，为完成特定教学目标而形成的稳定且简洁的教学结构及操作范式. 受教育重演论[3]启发，我们可以把学生的学习过程当作是对人类文化发展过程的一种认知意义上的重演.因此，我们的教学模式也就可以取自人类科学研究的形式. 回顾历史，我们发现科学研究主要存在两种形式：一种是由实验到方程、规律直至整个理论体系（如经典力学、电磁学、热力学等），即探究归纳法；另一种是先建立方程、理论框架，然后再回到实验，由实验来验证理论的真伪（如相对论、量子力学、粒子物理学等），即演绎验证法. 那么，我们在压强表达式的建立过程中，应当采用哪种教学模式呢？科学方法中心论指出，学科方法是教学模式的主体，是教学脉络的体现者，整个教学过程都要围绕学科方法进行[4]. 由此，我们有必要明晰两种学科方法与两种教学模式间存在的联系.采用对映的方法，我们可以将压强表达式建立的教学模式分为：以“控制变量—比例系数法”为主体的探究—归纳式教学和以“比值定义法”为主体的演绎—验证式教学.

（五）思维方法层面

思维方法是用于各种问题解决过程中的一般策略和方法，它属于特殊的心理体验，不能靠单纯的讲解来传授，往往需要使用、训练才能为学生体会、领悟[5]. 由于思维方法隐藏在学科方法的背后，对学科方法起支配与统摄的作用，所以思维方法的教育必须要借助学科方法来进行.因此，识别学科方法与思维方法之间的对应关系，无疑有利于我们通过学科方法对思维方法进行渗透式教学.结合两种学科方法的教学流程，如表1所示，可以发现，在使用“控制变量法”前，首先要利用生活实例让学生思考影响因变量的因素，这里便涉及了“猜想”这一非逻辑式的思维，接下来通过对实验数据的分析，得到因变量与自变量的比例关系，又需要用到“归纳”的思维，可见在使用控制变量—比例系数法建立物理概念时，调动了学生的“猜想”与“归纳”思维；反观比值定义法，先要结合学生已有认知结构，启发他们提出一种粗略描述物理概念的假设，然后设计实验验证假设，在否定先前假设的基础上找到不足并修改假设，由此通过一步一步的假设和演绎推理最终得出要定义的物理量.因此，无疑是“假设”“演绎”思维统摄着比值定义法.

综上所述，比值定义法与控制变量—比例系数法为学生重演了别样的研究范式，串联了迥异的认知路径，统摄了不同形式的教学模式，锻炼了学生思维的不同侧面.可见，两者均有其可取之处，它们适合于不同认知水平的学生.

维果茨基的“可接受性原则”指出，教学必须符合学生的年龄特征，以学生的成熟或准备为基础.这就要求我们在教学设计中必须考虑学生的已有认知水平，鉴于知识本身的难度是无法改变的.因此，我们须潜心研究主导知识建立的学科方法，对每一种学科方法的内涵与外延均应有清醒的认识，从而为不同认知水平的学生铺设出适合其思维发展的逻辑通道，最终实现教学流程与学生认知路径的合理对接，完成从“教学有法，教无定法”到“贵在得法”的三级跳跃.

参考文献：

[1] 郑渊方.压强概念的辨析与教学设计[J].物理教师，2014，35（12）：32-34.

[2] 石尧.对高中物理比值定义法和控制变量法的再思考[J].北京教育学院学报（自然科学版），2015，10（1）.

[3] 王全，母小勇.“科学史—探索”教学模式与“重演 ”论基础[J].课程·教材·教法，2008，28（7）：62-66.

[4] 邢红军.从知识中心到方法中心——科学教育理论的重要转变[J].首都师范大学学报（自然科学版），2011，32（6）：20-26.

[5] 陈清梅，邢红军，李正福.论物理课程改革背景下的科学方法教育[J].课程·教材·教法，2009（8）：52-56.