排列组合的简单应用
魏伟

【摘要】排列组合是一种基本的计数方法,在近代科学研究中有重要地位,从中小学现行的课程来看,是学生学习概率统计知识的基础,而且在安排调配等日常生活和工作中有大量应用。
【关键词】组合问题 组合模型 排列问题 排列模型 元素
【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089(2015)11-0136-02
一、排列组合的基本理论和公式
排列与元素的顺序有关,组合与顺序无关.如231与213是两个排列,而2+3+1的和与2+1+3的和是一个组合。 1.两个基本原理是排列和组合的基础
加法原理:做一件事,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+m3+…+mn种不同方法。
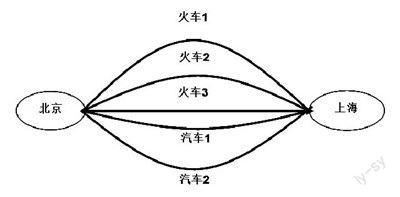
问题:从北京到上海,可以乘火车,也可以乘汽车。一天中火车有3班,汽车有2班.那么一天中,乘坐这些交通工具从北京到上海共有多少种不同的走法?
对于这个问题,首先要弄清楚这道题是要完成从北京到上海这件事,只要从北京到上海,就算完成了这件事.其次,从北京到上海有几类走法?
乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法。
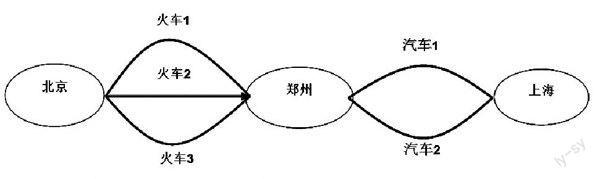
问题:从北京到上海,要从北京先乘火车到郑州,再于第二天从郑州乘汽车到上海,一天中从北京到郑州的火车有3班,从郑州到上海的汽车有2班,那么两天中,从北京到上海共有多少种不同的走法?
无论单独乘火车或汽车都不能从北京直接到达上海,要从北京到上海必须分两步,第一步要先到郑州,然后才能从郑州到达上海,只有这两步都完成了,才能从北京到达上海.从北京到郑州乘火车有3种走法,再从郑州到上海乘汽车有2种走法,并且两步依次完成后,才能到达上海,所以共有3×2 = 6种不同的走法。
这里要注意区分两个原理,要做一件事,完成它若是有n类办法,是分类问题,第一类中的方法都是独立的,因此用加法原理;做一件事,需要分n个步骤,步与步之间是连续的,只有将分成的若干个互相联系的步骤,依次相继完成,这件事才算完成,因此用乘法原理.这样完成一件事的分“类”和“步”是有本质区别的,因此也将两个原理区分开来。
2.排列
排列:从n个不同元素中,任取m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。从排列的意义可知,如果两个排列相同,不仅这两个排列的元素必须完全相同,而且排列的顺序必须完全相同,这就告诉了我们如何判断两个排列是否相同的方法。
3.组合
组合:从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从 n个不同元素中取出m个元素的一个组合。
从组合的定义知,如果两个组合中的元素完全相同,不管元素的顺序如何,都是相同的组合;只有当两个组合中的元素不完全相同时,才是不同的组合。
这里要注意排列和组合的区别和联系,从n个不同元素中,任取m(m≤n)个元素,“按照一定的顺序排成一列”与“不管怎样的顺序并成一组”这是有本质区别的。
二、用排列组合知识解决问题
最重要的是在计算式分析是分类还是分步,是排列还是组合问题,在分析中总结计算方法,进而归纳为排列组合问题,即利用排列组合公式计算。
1. 排列问题
例1:组数
用1、2两个数可以组成多少个不同的两位数?
可以组成12,21,2个两位数。
2×1=2(个)。
用1、2、3三个数可以组成多少个不同的两位数?
可以组成12,13,21,23,31,32,6个两位数。
3×2=6(个)。
用1、2、3、4四个数可以组成多少个不同的两位数?
猜想:4×3=12(个)?
可以组成12,13,14,21,23,24,31,32,34,41,42,43,12个两位数。
4×3=12(个)。
用1、2、3、4、5五个数可以组成多少个不同的两位数?
计算:5×4=20(个)。
用1、2、3、4、5......n个数可以组成多少个不同的两位数?
n×(n-1)(个)。
猜想:用1、2、3、4、5......n个数可以组成多少个不同的三位数?
n×(n-1)×(n-2)(个)。
猜想:用1、2、3、4、5......n个数可以组成多少个不同的n位数?
n×(n-1)×(n-2)…3×2×1=n!(个)。
上述猜想可以用数学归纳法验证验证,此类组数问题为排列问题,我们用排列数计算公式来计算。
2. 综合应用
例2:0,1,4,7和小數点可以组成多少个小于1的三位小数?
解析:整数部分只能是0,其余三个数字全排列P(3,3)=3×2×1=6(个)。
例3:由数字0、1、2、3、4按要求组数。
①可以组成多少个不同的五位数 ?
②小于20000的自然数。
①不同的五位数,分析最高位不能为0,所以最高位有4种选法,其余4个数字全排列(P4,4)=4×3×2×1=24,24×4=96(个)。
②小于20000的自然数 ,分析万位可以选择2,3,4,其余的四个数字全排列P(4,4)=4×3×2×1=24,24×3=72(个)。
例4 图中各有多少个三角形?
解析:图(1)中任意两条从A点引出线段都可以和线段BC上的一段组成一个三角形,是组合问题C(6,2)=6×5÷2=15(个)。
图(2)中第三条边可以是线段BC或线段DE的一部分,第三条边有两种选法,C(6,2)×C(2,1)=30(个)。
例5:用0、1、2、3、4、5、6、7、8、9这十个数字能够组成______个没有重复数字的三位数。
解析:用这十个数字排列成一个不重复数字的三位数时,百位上不能为0,故共有9种不同的取法.因为百位上已取走一个数字,所以十位上只剩下9个数字了,故十位上有9种取法。同理,百位上和个位上各取走一个数字,所以还剩下8个数字,供个位上取。
所以,组成没有重复数字的三位数共有9×9×8=648(个)。
例6:一个口袋中有4个球,另一个口袋中有6个球,这些球颜色各不相同,从两个口袋中各取1个球,共有多少种不同结果?
解析:从两个袋子里各选一个C(4,1)×C(6,1)=4×6=24(种)。
例7:有9名乒乓球运动员参加比赛,每两个运动员都要比赛一场,一共有多少场比赛?
解析:组合问题C(9,2)=9×8÷2=36(场).
例8:甲、乙、丙、丁四个同学排成一排,从左到右数,如果甲不排在第一个位置上,乙不排在第二个位置上,丙不排在第三个位置上,丁不排在第四个位置上,那么不同的排法共有______种。
解析:因每个人都不排在原来的位置上,所以,當乙排在第一位时,其他几人的排法共有3种;同理,当丙、丁排在第一位时,其他几人的排法也各有3种。因此,一共有9种排法。
例9:用1克、3克、9克三个砝码(砝码只能放在一个秤盘中),可以秤出几种不同重量的物体?
解析:是组合问题,分三类用1个砝码、2个砝码、3个砝码,C(3,1)+C(3,2)+C(3,3)=3+3+1=7(种)。
由于排列组合问题在生活中经常见到,在小学阶段很多问题要用到这方面的知识,所以在小学阶段掌握一些排列组合的知识对我们方便解决一些数学问题大有帮助,而在分析解决的过程中培养了学生的推理能力和有顺序地、全面地思考问题的能力。
参考文献:
[1]课程教材研究所,小学数学课程教材研究中心.数学 [M],北京:人民教育出版社出版,2004.6,第一版 .
[2]人民教育出版社中学数学室.数学 [M].北京:人民教育出版社出版,2003.6,第一版.第二册.
[3]张定强,吕世虎.高中新课程内容解析[M].北京:首都师范大学出版社,2004.9,第一版.
[4]傅龙骧.数学奥林匹克[M].兰州:兰州大学出版社,2005.2,第一版.
[5]魏有德.数学奥林匹克初级读本[M].成都:四川大学出版社,2000.6,第三版.

