采用横向铁磁交互作用的随机场伊辛模型的量子退火算法
张洪涛, 代永涛, 凃玲英
(1. 湖北工业大学 纳米电子技术与微系统实验室, 湖北 武汉 430068;
2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068)
采用横向铁磁交互作用的随机场伊辛模型的量子退火算法
张洪涛1,2, 代永涛1,2, 凃玲英1,2
(1. 湖北工业大学 纳米电子技术与微系统实验室, 湖北 武汉 430068;
2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068)
摘要:通过数值对角化分析瞬时基态和第一激发态,提出基于横向铁磁交互的量子退火的优势.采用贝特近似作为实际执行的算法,给出相应的模拟结果,并对传统量子退火、基于横向铁磁交互作用的量子退火和模拟退火算法的剩余误差进行比较.结果表明:所提算法能有效提高传统量子退火在随机场伊辛模型中的收敛速度;利用量子波动的选择空间可以有效实现量子退火的最佳性能.
关键词:横向铁磁交互作用; 随机场伊辛模型; 量子退火; 模拟退火
模拟退火算法(SA)[1]是基于Monte carlo迭代求解策略的一种随机寻优算法,已在生产调度、图像处理、控制工程等领域得到广泛应用[2-4].然而,经典模拟退火算法要跳出局部最小点A,到达全局最优点B,只能采用翻越势垒的方式实现.量子退火算法(QA)在其基础上,通过引入一个假的温度变量,实现在状态空间中搜索目标函数的最小值问题.它利用量子隧穿效应,直接从点A穿透势垒到达点B.因此,量子波动的性质被引入以伊辛(Ising)模型[5]为代表的经典优化问题中.与模拟退火算法相比,量子退火算法在退火收敛速度和避免陷入局部极小等方面具有一定优势,且适用于其他领域非线性最优化问题的求解.目前,实施量子退火有多种方式,如薛定谔方程的精确数值分析、量子蒙特卡罗模拟[6-7]和格林函数蒙特卡罗方法[8]等.然而,在一些研究中,常规量子态的量子退火在某些情况下已被证明不能有效地执行[9].本文研究一种基于横向铁磁交互作用的随机场伊辛模型的量子退火算法.
1横向铁磁交互作用
1.1 常规量子退火
量子退火[10-12]利用量子波动构建优化算法,使量子具有穿透比它自身能量高的势垒的能力,即量子隧穿效应.量子退火通过模拟这一过程实现对目标系统的优化.量子系统的演化公式为


式(1),(2)中:H(t)为含时哈密顿量; |Ψ(t)〉为量子系统状态;为方便起见,取ћ=1;Hlc对应势能项;Hkin(t)为适合系统的含时量子动能项,其初值比较大,对应较大的量子波动,并按照某一进度表逐渐减小为零.
1.1.1横向随机场Ising模型横向随机场Ising模型[13-14]常被作为量子退火算法的测试模型, 其哈密尔顿量为
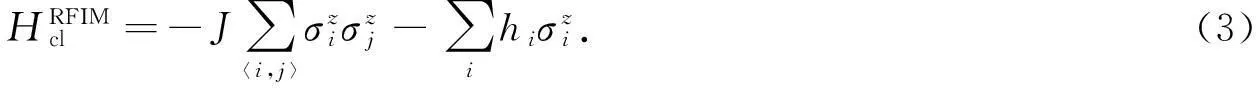


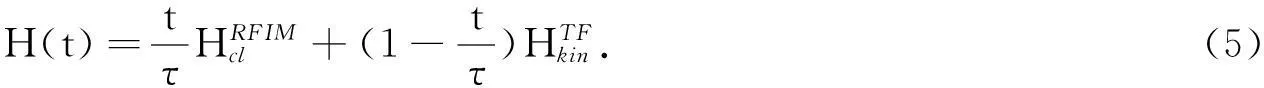
式(5)中:τ为退火时间.
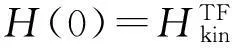
1.1.2绝热演化绝热演化[12-17]的定量准则为
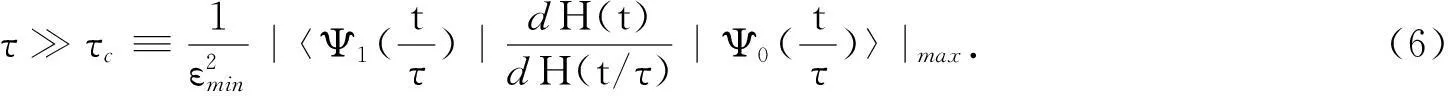
式(6)中:τc为特征时间;t/τ为时间参数;Ψ0和Ψ1分别为瞬时基态和第一激发态,其对应的能量分别记为E0(t),E1(t);εmin为瞬时基态与第一激发态间能量间隔的最小值,即εmin=[E1(t)-E0(t)]max.
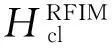

式(7)中:I为N维单位矩阵;量子系统的初态|Φ0〉为所有可能状态的等幅叠加态,即

式(8)中:N=2n对应于量子系统的Hilbert空间的维数,n为量子数.
1.2 横向铁磁交互作用
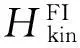

此时,时变哈密顿量为

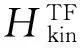
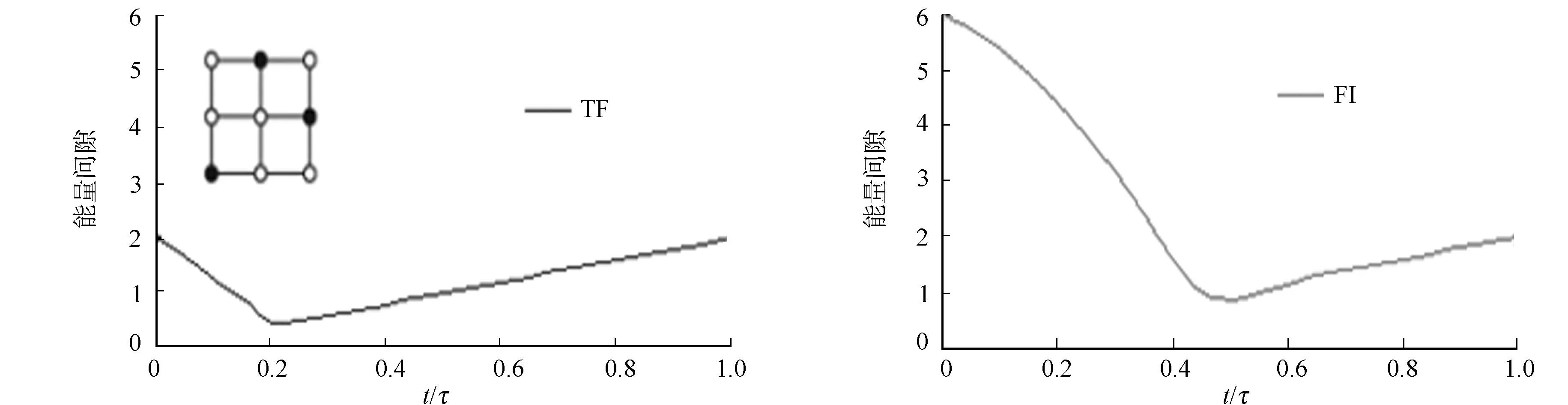
(a) 横向铁磁交互作用 (b) 常规横向场作用图1 基态与第一激发态之间的瞬时能量间隙Fig.1 Instantaneous energy gaps between the ground state and first excited state
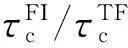
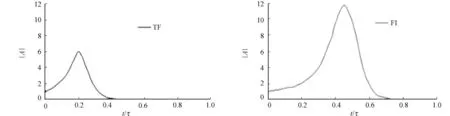
(a) 横向铁磁交互作用 (b) 常规横向场作用图2 矩阵元素的绝对值Fig.2 Absolute values of the matrix elements
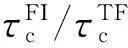
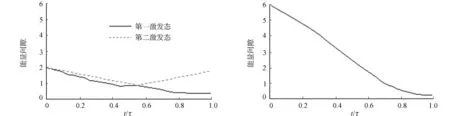
(a) 横向铁磁交互作用 (b) 常规横向场作用图3 基态与第一、二激发态之间的瞬时能量间隙Fig.3 Instantaneous energy gap between the ground state and the first and second excited states
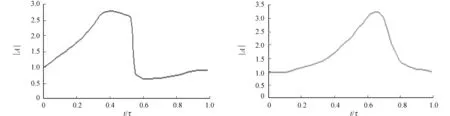
(a) 横向铁磁交互作用 (b) 常规横向场作用图4 矩阵元素的绝对值Fig.4 Absolute values of the matrix elements
2贝特近似的平均场退火
为了用平均场类型的方法实现最佳结果,采用贝特近似[18-19]代替简单的单体平均场理论.此时,其含时哈密顿量、势能项和量子动能项分别为
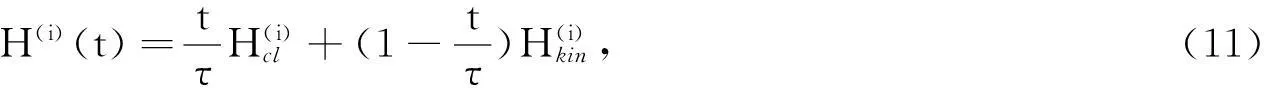
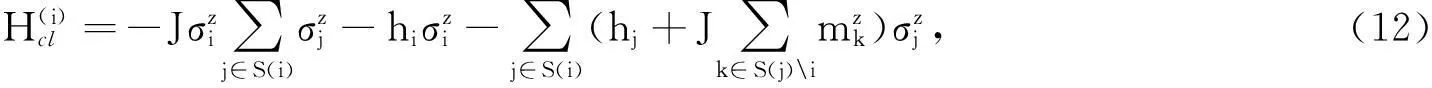
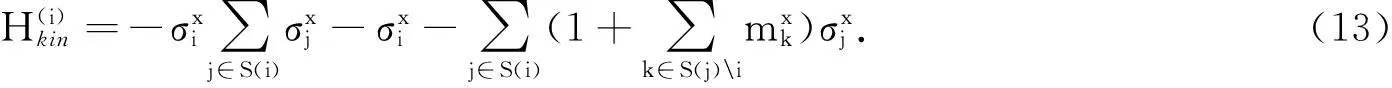
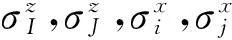
线性退火表T=T0·(1-t/τ).其中,T0是一个足够高的初始温度.将上述方法应用到100×100的二维随机场伊辛模型中,通过近似能量与一个完善算法而估计的真正的基态能量之间的差异计算剩余能量[20].基于横向铁磁交互作用的量子退火算法(TF)、模拟退火算法(Thermal)和常规横向场量子退火算法(FI)等3种退火算法在横向场随机Ising模型下的剩余能量,如图5所示.由图5(a)可知:基于横向铁磁交互作用的量子退火算法远远优于模拟退火算法和常规横向场量子退火算法;模拟退火算法与常规横向场量子退火的执行效果几乎相似,但前者略优于后者,可能是由于热近似和量子退火影响的差异造成的.由图5(b)可知:3种退火算法执行效果的差异性明显减少.
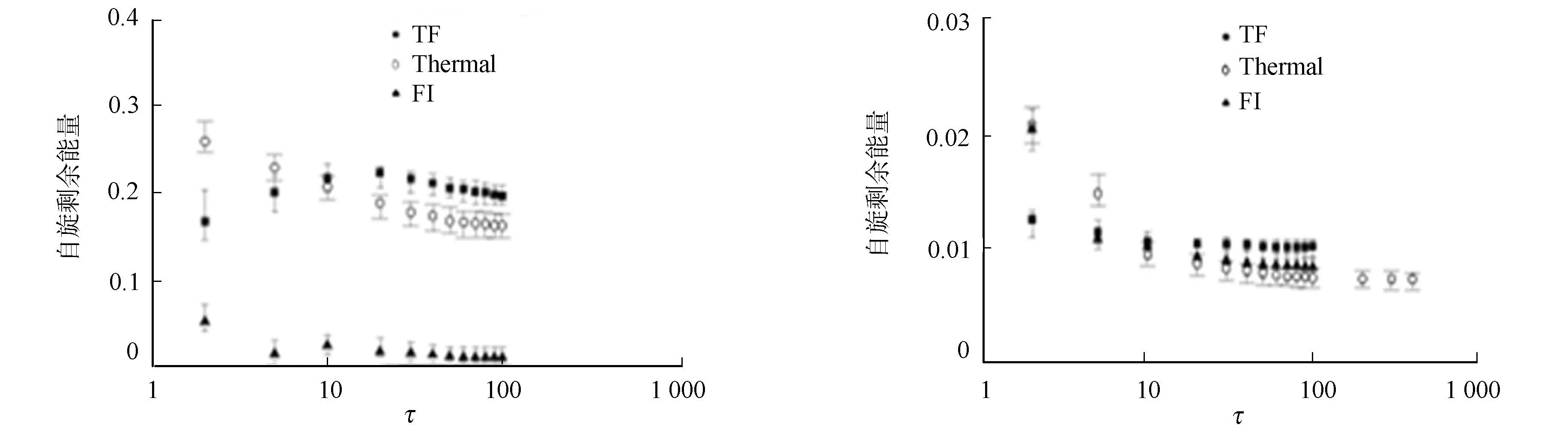
(a) J=2.0 (b) J=0.6图5 3种退火算法在横向场随机Ising模型下的剩余能量Fig.5 Residual energy of 3 kinds of annealing algorithm in the random transverse field Ising model
综上所述,当耦合常数J较大时,基于横向铁磁交互作用的量子退火算法更加有效,其中,真正的基态是完全或接近的铁磁性状态.横向铁磁交互作用的引入不一定改善了无序基态的结果.
3结束语
对横向铁磁交互作用的随机场伊辛模型的量子退火算法进行研究.结果表明:当J值较大时,基于横向铁磁交互作用的量子退火的效率高于其他两种方案.这意味着先前报道的铁磁基态的常规量子退火效率降低不是量子退火的一个内在特征,利用适当的量子效应可以得到比模拟退火更高的效率.利用量子波动的选择空间提取量子退火中的最佳性能非常重要,这种灵活性是量子退火的一个突出特性.
参考文献:
[1]杜卫林,李斌,田宇.量子退火算法研究进展[J].计算机研究与发展,2008,45(9):1501-1508.
[2]王凌.智能优化算法及其应用[M].北京:清华大学出版社,2004:17-35.
[3]张德富,彭煜,朱文兴,等.求解三维装箱问题的混合模拟退火算法[J].计算机学报,2009,32(11):2147-2156.
[4]KIRKPATRICK S C,GELATT C D,VECCHI M P,et al.Optimizationby simulated annealing[J].Science,1983,220(4598):671- 680.
[5]HOPFIELD J J,TANK D W.Computation of decisions: A model[J].Science,1986,233(4764):625-633.
[6]KADOWAKI T.Study of optimization problems by quantum annealing[D].Tokyo:Tokyo Institute of Technology,2002:15-40.
[7]MARTONAK R,SANTORO G E,TOSATTI E.Quantum annealing by the path-integral Monte carlo method: The two-dimensional random Ising model[J].Physical Review B,2002,66(9):351-363.
[8]LORENZO S,SANTORO G E.Quantum annealing of an Ising spin-glass by Green′s function Monte carlo[J].Physical Review E,2007,75(3):036703.
[9]SARJALA M,PETAJA V,ALAVA M.Optimization in random field Ising models by quantum annealing[J].Journal of Statistical Mechanics:Theory and Experiment,2006,16(1):79-107.
[10]KADOWAKI T,NISHIMORI H.Quantum annealing in the transverse Ising model[J].Physical Review E,1998,58(5):5355.
[11]BOIXO S,ALBASH T,SPEDALIERI F M,et al.Experimental signature of programmable quantum annealing[J].Nature Communications,2012,4(3):131-140.
[12]BOIXO S,RONNOW T F,ISAKO S V,et al.Evidence for quantum annealing with more than one hundred qubits[J].Nature Physics,2014,10(3):218-224.
[13]FYTAS N G,MARTIN-MAYOR V.Universality in the three-dimensional random-field Ising model[J].Phys Rev Lett,2013,110(1):019903.
[14]黄纯青,邓绍军.三维Ising模型的蒙特卡罗模拟[J].计算物理,2009,26(6):937-941.
[15]张映玉,付樟华.绝热量子优化算法研究进展[J].计算机工程与科学,2015,37(3):429-433.
[16]曹怀信,王素媛.量子绝热定理研究[J].纺织高校基础科学学报,2015,28(2):131-138.
[17]CAO Huaixin,GUO Zhihua,CHEN Zhengli.CPT-frames for non-Hermitian Hamiltonians[J].Commun TheorPhys,2013,60(9):328-334.
[18]SEMKIN S V,SMAGIN V P.Bethe approximation in the Ising model with mobile impurities[J].Physics of the Solid State,2015,57(5):943-948.
[19]MEILIKHOV E Z,FARZETDINOVA R M.Effective field theory for disordered magnetic alloys[J].Physics of the Solid State,2014,56(4):707-714.
[20]ALAVAl M,DUXBURY P,MOUKARAEL C,et al.Exact combinatorial algorithms: Ground states of disordered systems[M].New York:Phase Transitions and Critial Phenomena,2001:143-317.
(责任编辑: 钱筠英文审校: 吴逢铁)

Quantum Annealing of the Random-Field Ising Model
Based on Transverse Ferromagnetic Interactions
ZHANG Hongtao1,2, DAI Yongtao1,2, TU Lingying1,2
(1. Nanoelectron Technology and Micro-system Laboratory, Hubei University of Technology, Wuhan 430068, China;
2. School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China)
Abstract:Through the numerical analysis of the instantaneous ground state and the first excited state, the advantages of quantum annealing based on the transverse ferromagnetic interactions are presented. Using the Bethe approximation as an algorithm for practical implementation, the simulation results are given accordingly. Then the residual errors of conventional quantum annealing, quantum annealing by transverse ferromagnetic interactions, and simulated annealing are compared. The results show that the proposed algorithm can effectively improve the convergence speed of traditional quantum annealing in the random-field Ising model. And the best performance of quantum annealing can be achieved by using the choice space of the quantum fluctuation.
Keywords:transverse ferromagnetic interactions; random-field Ising model; quantum annealing; simulated annealing
基金项目:湖北省武汉市科技局“十城千辆新动力汽车计划”基金资助项目(2013011801010600)
通信作者:张洪涛(1963-),男,教授,博士,主要从事量子通信及计算技术、嵌入式视频监控系统和数字信号处理的研究.E-mail:zhanght@mail.hbut.edu.cn.
收稿日期:2015-09-18
中图分类号:TP 301
文献标志码:A
doi:10.11830/ISSN.1000-5013.2016.01.0007
文章编号:1000-5013(2016)01-0007-05

