采用非线性尺度空间滤波和SIFT的遥感影像配准方法

施文灶， 毛政元

(1. 福州大学 空间数据挖掘与信息共享教育部重点实验室， 福建 福州 350002；

2. 福建师范大学 光电与信息工程学院， 福建 福州 350108；

3. 福州大学 地理空间信息技术国家地方联合工程研究中心， 福建 福州 350002；

4. 福州大学 福建省空间信息工程研究中心， 福建 福州 350002)



采用非线性尺度空间滤波和SIFT的遥感影像配准方法

施文灶1,2,3,4， 毛政元1,3,4

(1. 福州大学 空间数据挖掘与信息共享教育部重点实验室， 福建 福州 350002；

2. 福建师范大学 光电与信息工程学院， 福建 福州 350108；

3. 福州大学 地理空间信息技术国家地方联合工程研究中心， 福建 福州 350002；

4. 福州大学 福建省空间信息工程研究中心， 福建 福州 350002)

摘要：针对传统点特征匹配算法存在运算时间长和配准精度低的问题，提出一种基于非线性尺度空间滤波和尺度不变特征转换(SIFT)点特征配准算法.首先，通过非线性尺度空间滤波对基准影像和待配准影像分别进行预处理，保留其边缘信息并去除噪声.其次，采用SIFT算法对预处理后的两幅影像进行特征点提取，通过最近邻和次近邻的欧式距离比值法进行双向匹配，得到匹配特征点.最后，对待配准影像进行仿射变换.结果表明：该方法的总体运行时间比传统SIFT点特征配准算法降低63.2%，且配准精度大幅提高.

关键词：遥感影像； 非线性尺度空间滤波； 尺度不变特征转换； 配准； 仿射变换

遥感影像配准是遥感影像变化检测、多源数据融合、运动检测和目标识别等一系列应用研究涉及的核心内容[1-4].提高配准的质量与自动化程度对于充分挖掘和有效利用海量遥感影像数据的地理信息具有极其重要的意义.平均平方差、统计相关、归一化互相关、不变矩、快速傅里叶变换相关等基于灰度的传统配准方法，虽然在一些中低分辨率遥感影像的配准中得到广泛的应用，但这类方法存在灰度变化敏感、抗噪性能差和计算复杂度高等缺点，应用范围受到严重制约.针对这些问题，一些学者提出基于点特征的遥感影像配准算法[5-15].然而，当待配准影像存在较大的几何变形时，基于点特征的配准算法的正确匹配率明显下降.此外，该类方法应用于高空间分辨率遥感影像配准时，存在大量的错误匹配点.本文提出一种基于非线性尺度空间滤波和尺度不变特征转换(SIFT)的影像配准方法.

1基本原理

基于非线性尺度空间滤波和SIFT影像配准方法的算法流程，如图1所示,包括基于非线性尺度空间滤波的预处理、SIFT特征点提取和特征点双向匹配等3个部分.

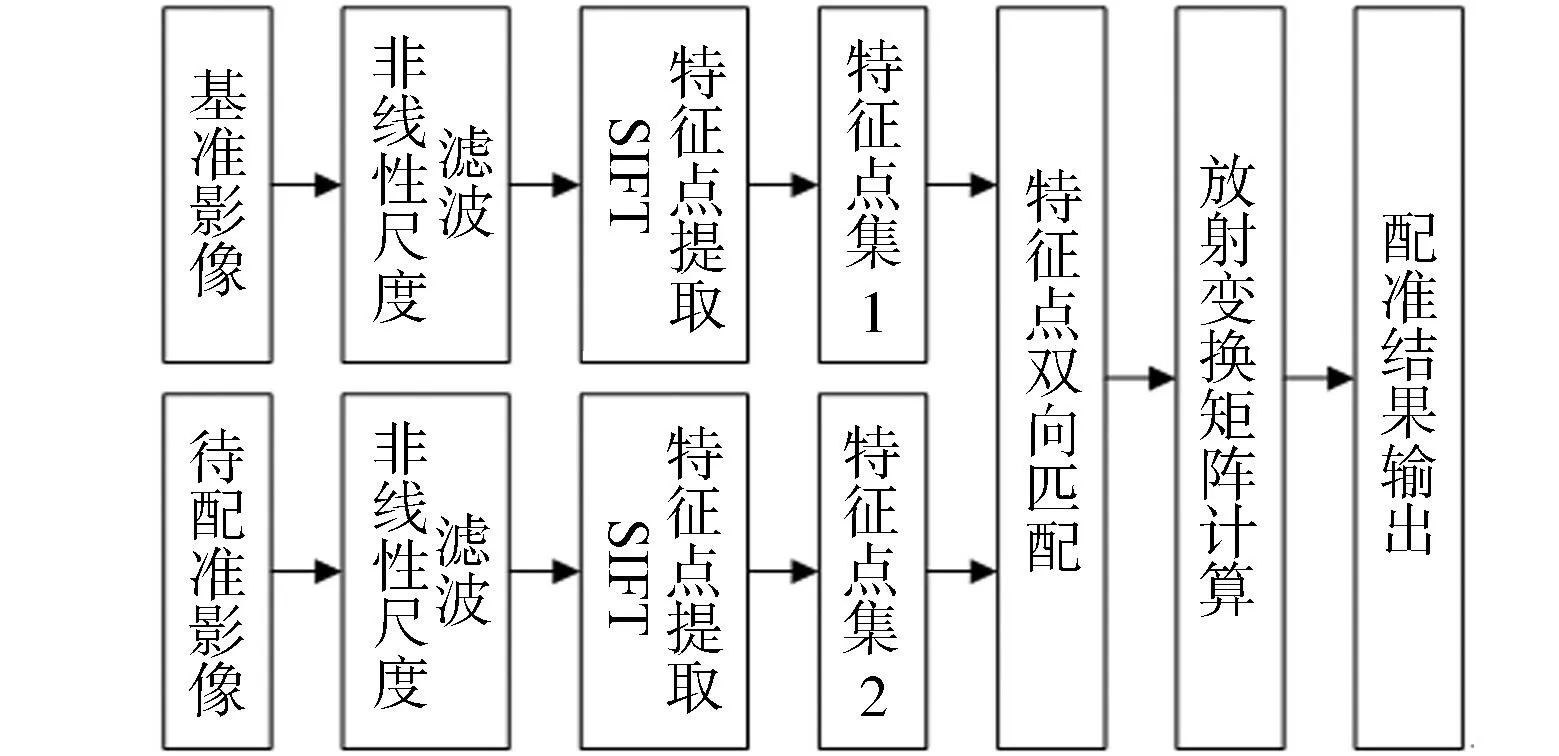
图1　算法流程图Fig.1　Flow chart of the algorithm

1.1　算法原理

非线性尺度空间滤波采用基于各向异性热扩散方程构造遥感影像的非线性尺度空间，其迭代方程为

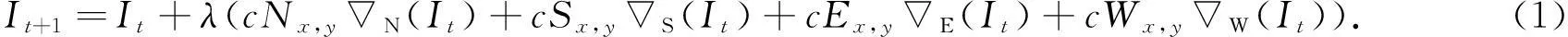
式(1)中:I为待处理的影像；N(It)，S(It)，E(It)，W(It)分别表示4个方向上的偏导，计算式为N(Ix,y)=Ix,y-1-Ix,y，S(Ix,y)=Ix,y-1+Ix,y，E(Ix,y)=Ix-1,y-Ix,y，W(Ix,y)=Ix+1,y-Ix,y，其取值越大，代表边界的可能性越大；cNx,y，cSx,y，cEx,y,cWx,y分别表示4个方向上的导热系数，计算式为cNx,y=exp(-(‖N(I)‖2/k2)，cSx,y=exp(-(‖S(I)‖2/k2)，cEx,y=exp(-(‖E(I)‖2/k2)，cWx,y=exp(-(‖W(I)‖2/k2)，当方向变化越大时，其取值越小，从而达到保留边缘的目的，k为方向平滑系数；λ为平滑控制系数，取值越大，影像越平滑，越不易保留边缘.

对遥感影像进行非线性尺度空间滤波，随着迭代次数增加，影像越平滑，像素之间的灰度差异越小，整幅影像的所有波段像素灰度标准差将减小.根据这一特点，验证标准差(δ)在不同λ和k的取值下，随迭代次数(n)的变化情况，如图2所示.

由图2(b)，(c)可知：λ，k的取值越小，整幅影像达到同一标准差(即相同的平滑程度)所需的迭代次数越多，运算量越大；随着λ，k的取值增大，部分边缘信息被滤除，综合信息量和计算量对算法效果的影响，通过对大量遥感影像进行实验，确定使算法平均效果达到最佳的λ，k的取值分别为0.15和15.00.

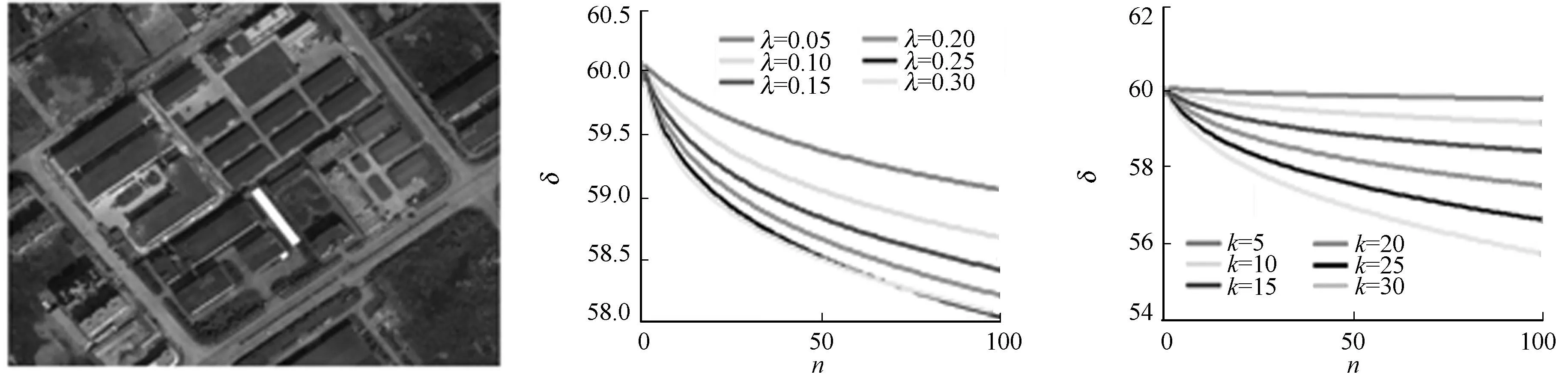
(a) 原图 (b) λ的不同取值 (c) k 的不同取值图2　标准差在不同λ和k的取值下随迭代次数的变化曲线Fig.2　Variation curve of standard deviation with diverse λ and k response to iterations

利用式(1)对图2(a)进行5 000次迭代，得到影像的标准差曲线，如图3所示.图3中：当迭代次数为782时，标注差曲线达到最小值33.6.为了实现迭代的自动停止，将标准差曲线出现第1个谷点作为迭代的停止判断条件.

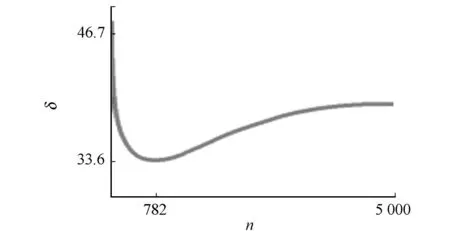
图3　标准差随迭代次数的变化曲线　Fig.3　Variation curve of standard deviation response to iterations

1.2　SIFT算法

SIFT算法[16-17]是一种提取局部特征的算法，在尺度空间寻找极值点，提取位置稳定、尺度不变性、旋转不变性和较少亮度依赖的SIFT描述子,其算法流程，如图4所示.

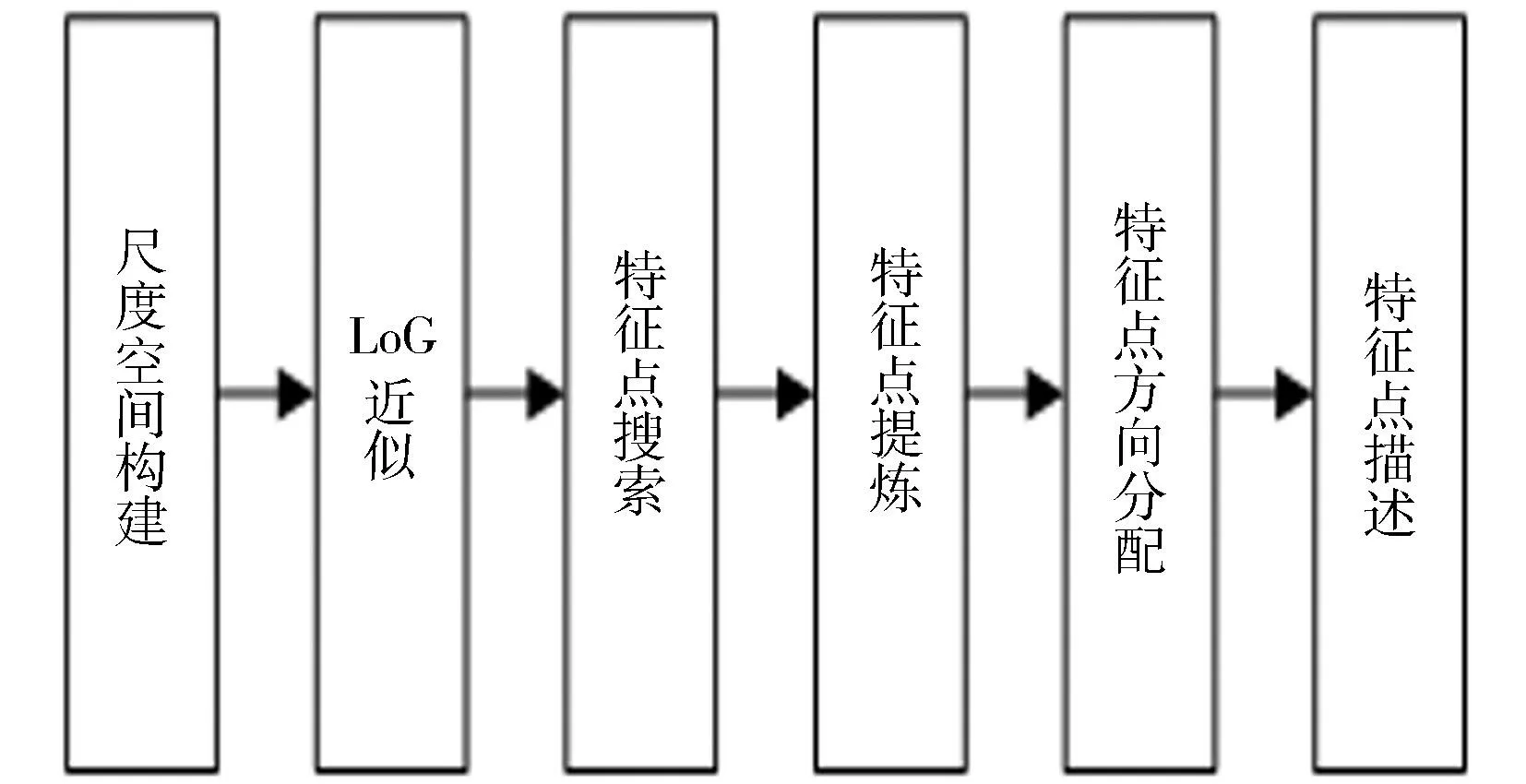
图4　SIFT算法流程图Fig.4　Flow chart of SIFT

图4中：尺度空间构建是一个初始化操作，通过生成尺度空间创建原始影像的多层表示,以保证尺度不变性；为了减少搜索特征点的计算量，通过高斯拉普拉斯(LoG)进行近似，可快速地检测到高斯差分(DoG)影像(尺度空间的每两幅相邻影像做减法操作)的极大极小值，即特征点.由于低亮度的区域是性能不好的特征点，所以使用Harris Corner检测器进行提炼，提高算法的鲁棒性；接着，为每个特征点分配一个方向，并做进一步计算，取消方向的影响，使算法具有旋转不变性；最后，利用位置上的尺度和旋转不变性，生成能够唯一地识别特征点的向量，即描述子.为得到这样的SIFT描述子，算法将特征点周围16 px×16 px的窗口分解为16个4 px×4 px的子窗口.在每个4 px×4 px的子窗口中，计算出梯度的大小和方向，并用一个8个柱体的直方图统计子窗口的平均方向，得到一个128维的向量，并对其进行归一化.

1.3　特征点双向匹配

搜索图1的特征点集1到特征点集2中的所有满足条件的特征点，记为S1；反之，搜索图1的特征点集2到特征点集1中所有满足条件的特征点，记为S2.其计算方法为

式(2)中:lnearest为特征点的最近邻欧式距离;lS-nearest为特征点的次近邻欧式距离；distRatio为阈值，取值越小，则满足条件的特征点向量描述越接近，产生误匹配点的可能性越大，反之，取值越大，可以提高匹配点的正确性，文中将其设定为0.7.通过计算，将S=S1∩S2作为特征匹配点.

2试验与分析

试验采用的计算机CPU为AMD Athlon(tm) Ⅱ X2 245，2 GB内存，操作系统为Windows XP.采用Matlab R2012a进行算法的编程和调试.试验数据为2012年11月6日和2012年8月1日深圳市的两期PLEIADES影像，包含红、绿、蓝3个波段，分辨率为0.5 m·px-1，各选取600 px×600 px的试验区域，分别记为1#影像和2#影像，该区域内包含了绿色植被、永久性建筑物和临时性建筑物等类型.

比较SIFT-BM(SIFT+双向匹配)和NSF-SIFT-BM(非线性尺度空间滤波+SIFT+双向匹配)两种配准方法的性能，其效果对比图，如图5所示.图5中：x,y为坐标轴.以1#影像为基准影像，2#影像为待配准影像，利用算法提取的匹配点对2#影像进行仿射变换.为了比较配准前后的效果，利用canny算子分别提取1#影像、2#影像和仿射变换后的2#影像的边缘，并进行叠加，如图5(e)所示.由图5(e)可知：配准前的1#影像(深色)和2#影像(浅色)中同一地物的边缘在空间位置上偏离较大，说明两幅影像之间的配准程度低.

应用SIFT-BM进行影像配准，影像之间存在较多的误配准对，如图5(a)所示，得到的2#影像仿射变换结果及其边缘与2#影像的边缘叠加,如图5(c)，(f)所示.显然，SIFT-BM配准算法完全失败.

应用NSF-SIFT-BM进行影像配准，如图5(b)所示.由图5(b)可知：两幅影像之间共有7对匹配点，且均是正确的同名点(方块).仿射变换后的2#影像与1#影像的配准程度非常好，如图5(d)所示.由于两期影像中拍摄角度和气候条件等方面存在差异，因此，用canny边缘检测算法提取的边缘相差较大.但对于图5(g)中两幅影像保留较为完整的边缘部分(椭圆包含的区域)，其边缘接近完全重合，说明NSF-SIFT-BM处理后的影像配准精度较高.

(a) SIFT-BM (b) NSF-SIFT-BM (c) SIFT-BM仿射变换

(d) NSF-SIFT-BM仿射变换 (e) 配准前两幅影像的边缘叠加 (f) SIFT-BM配准后 (g) NSF-SIFT-BM配准后图5　SIFT-BM和NSF-SIFT-BM配准算法效果对比Fig.5　Registration algorithm effect comparison of SIFT-BM and NSF-SIFT-BM

为了更合理地对比两种配准算法的配准精度，提出一种基于算法仿射变换矩阵均方误差(AT-MSE)的方法对其进行评价.AT-MSE可以衡量待配准影像的配准结果相对于基准影像的变化程度，其值越小，说明算法仿射变换矩阵对应的配准模型具有更好的精确度.两幅相同影像之间的的期望仿射变换矩阵为

定义

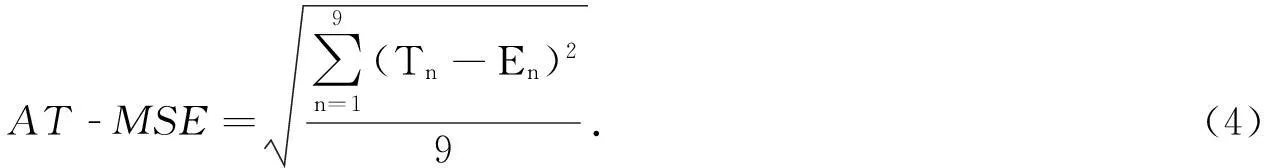
式(4)中:Tn，En分别为算法仿射变换矩阵和期望仿射变换矩阵的元素取值.SIFT-BM和NSF-SIFT-BM的算法性能参数对比，如表1所示.表1中：n1为SIFT特征点数；n2为双向匹配后的特征点数；t为运行时间.

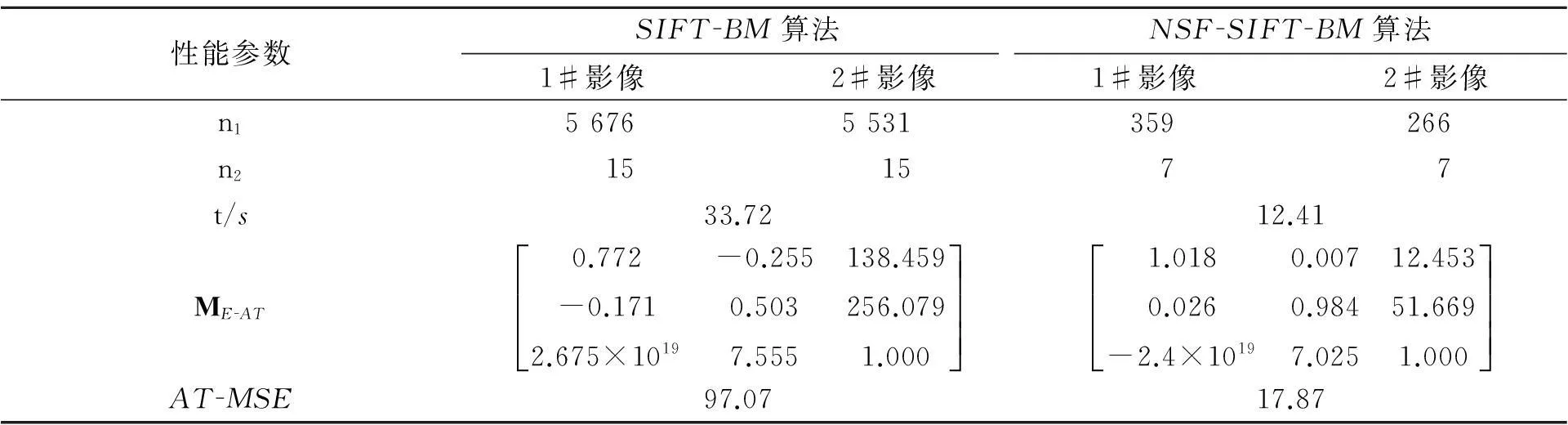
表1　SIFT-BM和NSF-SIFT-BM的性能对比

由于高分辨率遥感影像普遍存在“同物异谱”和“异物同谱”现象，直接采用SIFT算法提取不变特征，会得到大量的错误匹配点，严重影响配准精度.因此，通过非线性尺度空间滤波预处理去除噪声的同时，可保留边缘信息，使提取的SIFT特征点具有数量少、抗仿射变换强等优点，减少了匹配的运算量.由表1可知：通过非线性尺度空间滤波进行预处理，两幅影像的特征点数分别从5 676和5 531减少为359和266；NSF-SIFT-BM算法总体的运行时间比SIFT-BM降低了63.2%；AT-MSE从97.07下降到17.87，表明配准精度有了显著的提升.由于能够保证用NSF-SIFT-BM提取的SIFT特征点数远少于用SIFT-BM提取的SIFT特征点数，因此，如果增大图像尺寸，算法缩短配准时间的优势依然存在.

3结束语

针对高分辨率遥感影像提出一种基于非线性尺度空间滤波和SIFT的配准方法，并通过双向匹配筛选特征点提高准确性，为基于点特征的遥感影像配准提供新的思路与实现途径.试验结果表明：文中方法具有特征点搜索空间小、参数易确定、算法时间复杂度低等优势，在克服现有基于点特征的遥感影像配准方法普遍存在的自动化程度低、计算量大、抗干扰能力弱等局限性的同时，提高了配准精度.后续研究将考虑把算法扩展至大幅面高分辨率遥感影像之间的配准.

参考文献：

[1]BROWNLG.Asurveyofimageregistrationtechniques[J].AcmComputingSurveys,1992,24(4):325-376.

[2]ZITOVAB,FLUSSERJ.Imageregistrationmethods:Asurveyimageviscomput[J].ImageandVisionComputing,2003,21(11):977-1000.

[3]POHLC,VanGENDERENJL.Reviewarticlemultisensorimagefusioninremotesensing:Concepts,methodsandapplications[J].InternationalJournalofRemoteSensing,1998,19(5):823-854.

[4]HOLDENM.Areviewofgeometrictransformationsfornonrigidbodyregistration[J].IEEETransactionsonMedicalImaging,2008,27(1):111-128.

[5]张迁,刘政凯,庞彦伟,等.基于SUSAN算法的航空影像的自动配准[J].测绘学报,2003,32(3):245-250.

[6]罗楠,孙权森,耿蕾蕾,等.一种扩展SURF描述符及其在遥感图像配准中的应用[J].测绘学报,2013,42(3):383-388.

[7]YANWeidong,SHEHongwei,YUANZhanbin.RobustregistrationofremotesensingimagebasedonSURFandKCCA[J].JournaloftheIndianSocietyofRemoteSensing,2014,42(2):291-299.

[8]TEKEM,TEMIZELA.Multi-spectralsatelliteimageregistrationusingscale-restrictedSURF[C]∥20thInternationalConferenceonPatternRecognition.Istanbul:IEEEPress,2010:2310-2313.

[9]SONGZhili,ZHANGJunping.RemotesensingimageregistrationbasedonretrofittedSURFalgorithmandtrajectoriesgeneratedfromLissajousfigures[J].GeoscienceandRemoteSensingLetters,2010,7(3):491-495.

[10]KIMAL,SONGJH,KANGSL,etal.Matchingandgeometriccorrectionofmulti-resolutionsatelliteSARimagesusingSURFtechnique[J].KoreanJournalofRemoteSensing,2014,30(4)：431-440.

[11]岳春宇,江万寿.几何约束和改进SIFT的SAR影像和光学影像自动配准方法[J].测绘学报,2012,41(4):570-576.

[12]YULe,ZHANGDengrong,HOLDENEJ.Afastandfullyautomaticregistrationapproachbasedonpointfeaturesformulti-sourceremote-sensingimages[J].ComputersandGeosciences,2008,34(7):838-848.

[13]ZHENGYi,CAOZhiguo,XIAOYang.Multi-spectralremoteimageregistrationbasedonSIFT[J].ElectronicsLetters,2008,44(2):107-108.

[14]GONCALVESH,CORTE-REALL,GONCALVESJA.AutomaticimageregistrationthroughimagesegmentationandSIFT[J].IEEETransactionsonGeoscienceandRemoteSensing,2011,49(7):2589-2600.

[15]HASANM,JIAX,ROBLES-KELLYA,etal.Multi-spectralremotesensingimageregistrationviaspatialrelationshipanalysisonsiftkeypoints[C]∥GeoscienceandRemoteSensingSymposium.Honolulu:IEEEPress, 2010:1011-1014.

[16]LOWEDG.Objectrecognitionfromlocalscale-invariantfeatures[C]∥TheProceedingsoftheSeventhIEEEInternationalConferenceonComputerVision.Kerkyra:IEEEPress,1999:1150-1157.

[17]LOWEDG.Distinctiveimagefeaturefromscaleinvariantkeypoints[J].InternationalJournalofComputerVision,2004,60(2):91-110.

(责任编辑： 钱筠英文审校： 吴逢铁)

RemotelySensedImageryRegistrationBasedon

NonlinearScale-SpaceFilteringandSIFT

SHIWenzao1,2,3,4，MAOZhengyuan1,3,4

(1.KeyLabofSpatialDataMiningandInformationSharingofMinistryofEducation,FuzhouUniversity,Fuzhou350002,China;

2.CollegeofPhotonicandElectronicEngineering,FujianNormalUniversity,Fuzhou350108,China;

3.NationalEngineeringResearchCentreofGeospatialInformationTechnology,FuzhouUniversity,Fuzhou350002,China;

4.SpatialInformationEngineeringResearchCentreofFujianProvince,FuzhouUniversity,Fuzhou350002,China)

Abstract：To solve the problems of long executing time and low registration accuracy of the traditional point feature matching algorithm, this article proposed an improved scale-invariant feature transform (SIFT) point feature matching approach based on the nonlinear scale-space filtering. Firstly, the reference image and the to-be-registered one were respectively preprocessed with the nonlinear scale-space filter filtering. Secondly, feature points were extracted from the two images by means of the SIFT algorithm. Then, matched feature points were obtained through a bilateral matching by the ratio of Euclidean distances of the nearest neighbor to that of the next nearest one. Finally, an affine transformation was carried out to the to-be-registered image. Experimental results show that the executing time of the proposed method reduces 63.2% compared with the traditional SIFT point feature matching algorithm, and the registration accuracy is significantly improved.

Keywords：remotely sensed imagery； nonlinear scale-space filtering； scale-invariant feature transform； registration； affine transformation

基金项目：国家自然科学基金资助项目(61275006， 41201427)； “十二五”国家科技支撑计划项目(2013BAC08B02-01)； 国家重点基础研究发展计划项目(2006CB708306)； 福建省教育厅科研基金资助项目(JB14038)

通信作者：施文灶(1982-)，男，讲师，博士研究生,主要从事高空间分辨率遥感影像信息提取的研究.E-mail:swz@fjnu.edu.cn.

收稿日期：2015-09-10

中图分类号：P 237

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0038

文章编号：1000-5013(2016)01-0038-05