福建省全社会固定资产投资预测研究——基于ARIMA模型与二次指数平滑法的应用

林雅娜,黄显钧

(福建农林大学经济学院，福建 福州 350002)

福建省全社会固定资产投资预测研究——基于ARIMA模型与二次指数平滑法的应用

林雅娜,黄显钧

(福建农林大学经济学院，福建 福州 350002)

[摘要]运用ARIMA模型与二次指数平滑法对福建省固定资产投资进行试预测,结果表明,受政策变动影响,两种方法的预测结果均比实际值低,二次指数平滑法预测的误差过大,两种方法都存在中长期预测误差变大的问题。在政策环境稳定的前提下,运用ARIMA(4,2,4)模型与二次指数平滑法对福建省2015-2017年固定资产投资进行预测,并对两种方法的预测值取平均值,得出预测结果。

[关键词]ARIMA模型;二次指数平滑法;固定资产投资;

收稿日期：*2015-07-03

黄显钧(1989—)，男，福建罗源，硕士研究生。研究方向：区域经济。

作者简介：林雅娜(1989—)，女，福建漳州，博士研究生。研究方向：农村金融。

[中图分类号]F830.59

[文献标识码]A

[文章编号]1008-4940(2015)05-0012-05

Abstract:This paper uses the methods of ARIMA model and second exponential smoothing method to make a trial prediction on fixed asset investment in Fujian. The result indicates that the forecast values of these two methods are lower than the actual values due to the influence of policy fluctuation, and there is a large deviation when using these two methods to do the medium and long-term forecast. On the assumption that the policy is relatively stable, the paper uses ARIMA(4,2,4) model and second exponential smoothing method to forecast the fixed asset investment of 2015-2017 in Fujian, then gets average value of two forecast values and reaches the forecast results.

一、文献回顾

固定资产投资作为我国经济增长的“三驾马车”之一，一直以来备受关注。近几年，在内需不振、出口受阻的大环境下，固定资产投资对经济增长的推动作用更加突出。福建省固定资产投资从2003年的1507.87亿元增加到2014年的18449.48亿元，平均增速26.2%，总体翻了12倍。虽然从2010年开始，福建省全社会固定资产投资增长速度放缓，但每年新增加的固定资产投资数额都在2000亿以上。2014年，福建省固定资产投资额占GDP的比值达到了75%，经济增长结构明显失衡①。通过合理的预测，可以把握未来固定资产投资的发展趋势，有利于控制福建省全社会固定资产投资的规模。

固定资产投资的预测方法较为丰富，目前国内学者使用的预测方法主要有ARIMA模[1-5]、Logistic模型[6]、灰色预测法[7-8]、人工神经网络预测法[9]、指数平滑模型[10]等等。石美娟(2005)认为传统的时间序列方法和ARIMA法在分析的前提条件、适用环境和建模的基本思想方面存在不同，认为使用ARIMA法来预测未来固定资产投资的效果更好[1]。陈悦华、廖造壮(2012)基于灰色预测理论，在拟合过程中引入新陈代谢思想，依次加入新数据的同时剔除较陈旧数据，构造新的原始数据序列，以提高拟合精度[8]。徐志勇、秦伟良、李奇松(2007)使用灰色预测法、Holter-Winter非季节指数平滑模型和分段线性回归模型，对江苏省“十一五”期间的全社会固定资产投资进行预测，结果表明分段线性回归模型具有较好的拟合效果[7]。现有研究的主要目的是提高预测精度，但较少从历史的角度对已预测结果进行检验，本文采取事后预测的方法对ARIMA模型和二次指数平滑模型的预测结果进行比较分析，并对福建省2015-2017年固定资产投资额进行短期预测。

二、对固定资产投资额的预测(事后预测)

1.模型介绍与数据来源

(1)ARIMA模型

ARIMA模型(Autoregressive Integrated Moving Average Model)，由Box和Jenkins于1978年提出，属于时间序列预测方法。一般来讲，如果数据不平稳，建立ARMA模型进行预测会出现偏差，通过对非平稳序列进行一次或多次差分，将其转化为平稳序列后再建立相应的模型，可以提高模型的精确度，这个过程表示为ARIMA(p,d,q)，其中，p为自回归项，d是差分次数，q为移动平均项数，AR指自回归，MA为移动平均。其一般表达式为：

yt=α0+α1yt-1+α2yt-2+…+αpyt-p+β0ut+β1μt-1+β2μt-2+…+βqμt-q

(1)

建立ARIMA模型首先得判断时间序列的平稳性，可以通过单位根检验、折线图、自相关函数图等来判断，一般来讲，经济运行的时间序列都不是平稳序列。如果数据不平稳，就需要对数据进行平稳化，通常做法是对数据先求对数再进行差分。时间序列平稳后，根据自相关函数和偏相关函数的特征建立相应的模型，如果偏相关函数是截尾的，自相关函数是拖尾的，则建立AR模型，相反则建立MA模型，若自相关函数和偏相关函数均是拖尾的，则建立ARMA模型，最后再进行参数估计和假设检验，确定最后的模型形式。

(2)二次指数平滑法

指数平滑法是一种时间序列分析预测法，主要通过计算指数平滑值，配合一定的时间序列预测模型对未来进行预测。一次指数平滑的预测值是实际值序列的加权平均，而且主要倚重近期样本数据，适用于比较平稳的序列。二次指数平滑是在一次指数平滑的基础上作进一步的平滑，当数据存在线性趋势时，用二次指数平滑预测较为理想[11]。二次指数平滑的计算公式为：

(2)

其中，St是一次指数平滑序列，Dt是二次指数平滑系列，α是平滑系数(0≤α≤1),yt是实际值序列。

指数平滑预测结果的好坏很大程度上取决于平滑系数α的取值。一般来讲，如果序列变化较为平缓，平滑系数宜取得小些，如果序列变化较为剧烈，平滑系数可取大些(如0.3~0.5)，如果序列有很强的趋势，平滑系数必须大于0.5才能跟上序列变化，可取0.6~0.8。

2.预测的有效性检验

本文首先运用ARIMA模型和二次指数平滑法对历史数据进行事后预测。采用1980-2009年的数据，分段预测2010-2012年和2010-2014年的固定资产投资额，前者代表短期预测，后者代表中长期预测，通过对比预测结果与真实值来看两种方法预测的有效性。

(1)ARIMA模型试预测

由图1可以看出福建省1980-2009年固定资产投资存在缓慢增长、平稳增长和迅速增长三个阶段。令福建省1980-2009年固定资产投资数额为时间系列{Zt}，运用Eviews8.0对{Zt}进行单位根检验，结果显示数列非平稳，需运用ARIMA模型进行预测。

首先要通过差分使非平稳系列{Zt}变成平稳系列。对{Zt}取对数，并进行单位根检验，结果显示，取对数后的{Zt}系列经过二阶差分后平稳。令二阶差分系列为{IIZ}，通过自相关和偏相关分析图(图2)可以看出自相关函数与偏相关函数均表现为拖尾，对{IIZ}进行均值是否为0的检验，结果不能拒绝均值为0的假设，即{IIZ}满足均值为0的假设，可以运用ARMA模型进行预测。通过运用AIC和SC原则进行p和q的选取，经过反复筛选，取p=4,q=4。模型参数与相关检验列于表1。

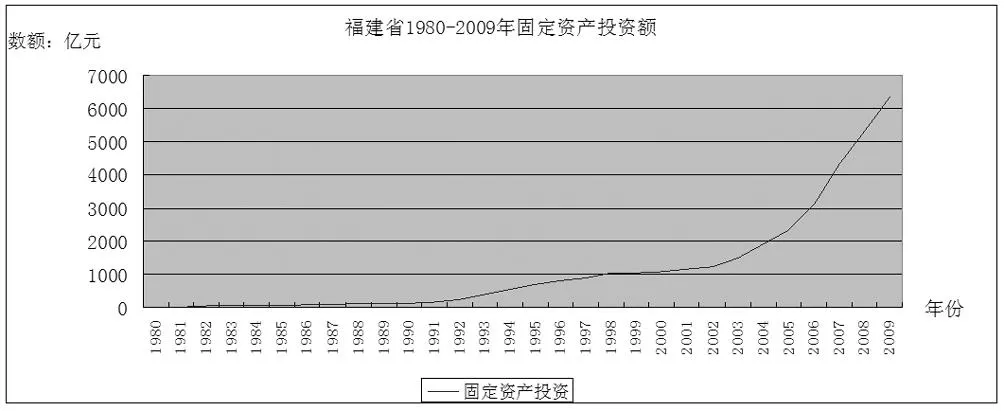
图1　福建省1980-2009年固定资产投产变化趋势

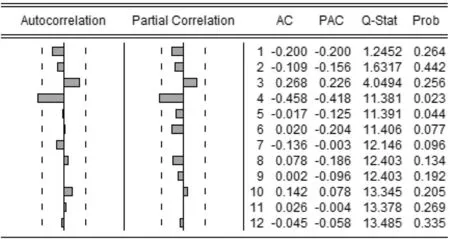
图2　自相关和偏相关分析图

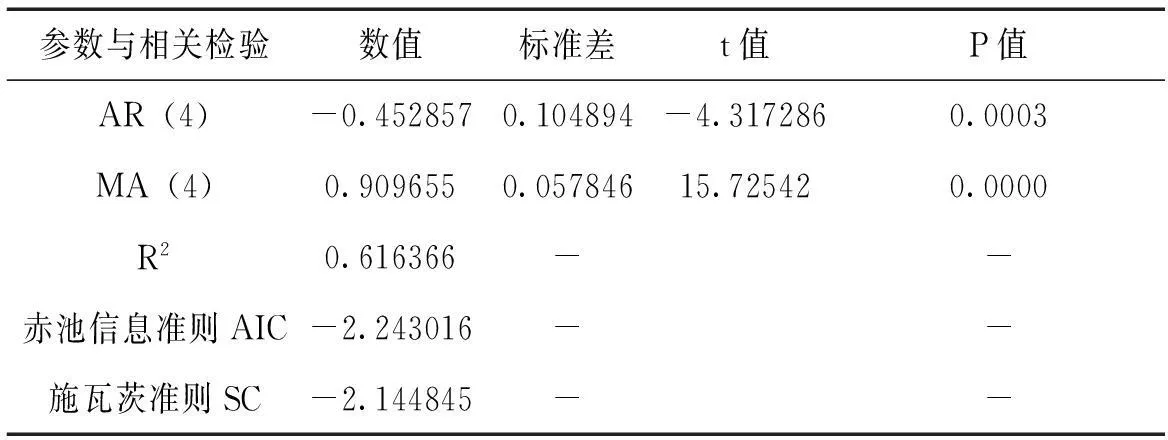
表1　模型参数估计与相关检验

利用ARIMA(4,2,4)模型对{Zt}做出2010-2012年和2010-2014年的静态预测值，与实际值进行比较，见表2和表3。

(2)二次指数平滑法试预测

从图1可以看到，福建省1980-2009年全社会固定投资短期内的上升趋势十分明显，此时采用二次指数平滑法可以较好地捕捉这种线性趋势，且平滑系数必须大于0.5以上才能跟上序列变化，本文取0.6~0.8之间的平滑系数进行预测，并结合平均绝对百分误差(MAPE)进行最后预测结果的选择。平均绝对百分误差(MAPE)是用百分数表示的预测误差指标，在实际运用中，MAPE越小，预测精度越高，如果MAPE超过10，则预测值的可信度大大降低。

(3)

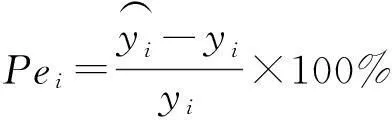
运用EViews 8.0对福建省1980-2009年全社会固定投资序列进行二次指数平滑，平滑系数设为0.8，预测2010-2012和2010-2014年的固定资产投资额，预测结果见表2和表3。

(3)试预测结果分析

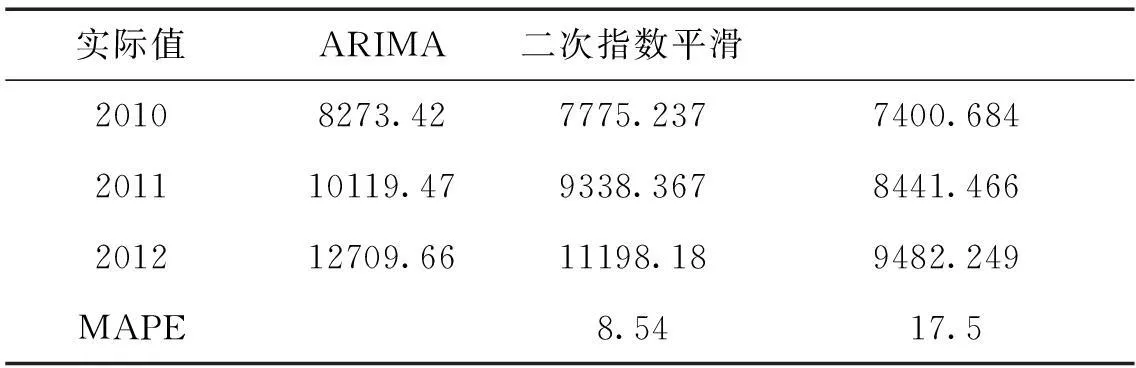
表2　福建省2010-2012年固定资产投资的预测值与实际值比较 (亿元)

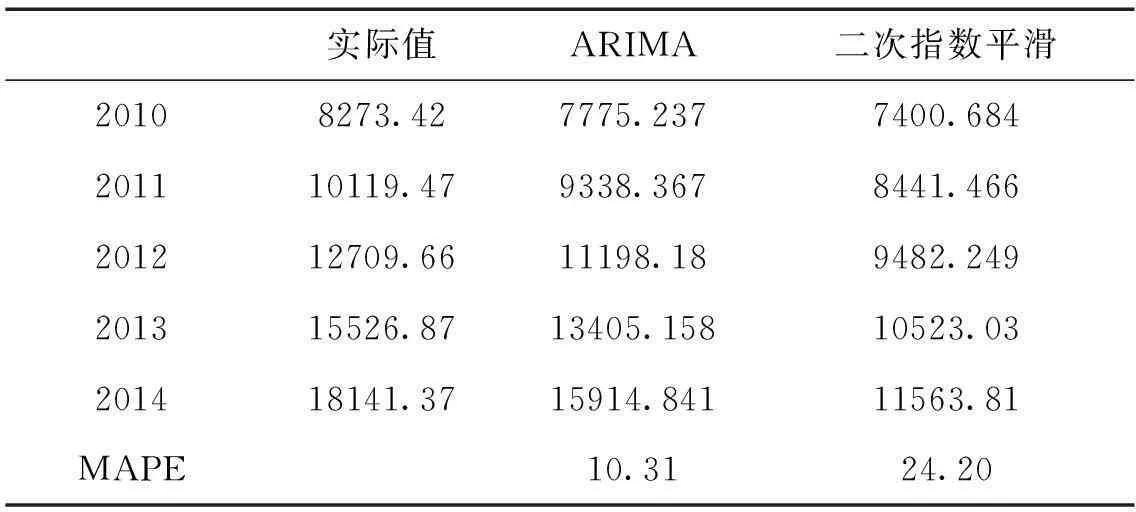
表3　福建省2010-2014年固定资产投资预测值与实际值比较 (亿元)

一般来讲，在运用ARIMA和二次指数平滑模型之前，大部分学者会进行试预测，但使用的预测期间包括了全部样本时间，所以试预测出来的预测值的MAPE值会相对较小，则认为样本的预测精度较高，可以进行预测。本文的不同之处是，站在2009年预测未来三年和未来五年的固定资产投资，但实际值已经了然于胸。从表2和表3可以看出，如果2009年有学者运用二次指数平滑法预测福建省2010-2012年或者2010-2014年的固定资产投资，则从已经发生的角度来看，这些值的MAPE值远远超过10，预测误差过大。而ARIMA在短期预测的精度则远远高过二次指数平滑法，但当预测期达到五年，其后期预测值的精度则明显下降。

究其原因，二次指数平滑法捕捉的是短期最新的趋势，所以如果按照历史的发展趋势，则固定资产投资实际值不会与预测值出现过大的偏差，但事前预测无法捕捉到预测期内的其他重要变动。2008年次贷危机之后，政府的经济刺激计划不断出台，增加固定资产投资成为拯救经济的快速通道，福建省固定资产投资增速始终保持在20%以上，2009年之后，福建省每年的固定资产投资净增加平均在2000亿左右，而在2009年以前的年份，固定资产投资每年的净增加基本上在1000亿以下，二次指数平滑并未捕捉到2009年及之后的这些变动，从现在来看，站在2009年运用二次指数平滑模型所做的固定资产投资的预测基本与现实不符，而ARIMA模型短期预测精度仍相对较高，预测结果与实际值的差距较小。

三、福建省2015-2017年固定资产投资预测

福建省固定资产投资近五年平均增速为23.3%，2014年固定资产投资额占GDP的比值达75%，经济增长结构明显失衡。随着自贸区、21世纪海上丝绸之路核心区等重大政策落地，未来福建省经济增长将有望逐步转向消费拉动与投资拉动并重的局面，固定资产投资增速与固定资产投资对经济增长的贡献将会面临调整。

鉴于固定资产投资长期预测的精度会下降，在未来政策与宏观经济环境相对稳定的前提假设下，本文运用ARIMA(4，2，4)模型与二次指数平滑法(平滑系数为0.8)对福建省2015-2017年固定资产投资额进行预测，所用的样本为福建省1980-2014年固定资产投资额，该时间序列为非平稳序列，经过二阶差分后平稳。预测结果如表4所示。

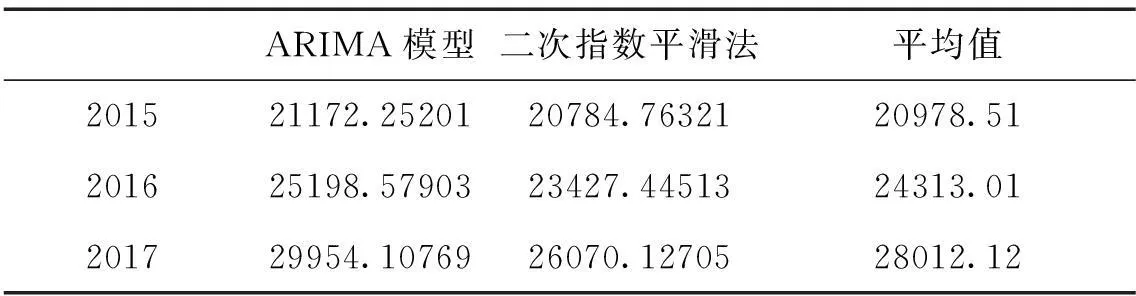
表4　福建省2015-2017年固定资产投资预测值(亿元)

综合表2、表3、表4来看，ARIMA模型的预测值普遍大于二次指数平滑法的预测值，在未来经济增长结构调整的趋势下，固定资产投资的增速预计会出现下降，本文最终取两种方法预测值的平均值，作为福建省2015-2017年固定资产投资预测的结果，即2015年固定资产投资额20978.51亿元，2016年为24313.01亿元，2017年为28012.12亿元。

四、结论

本文通过利用福建省1980-2009年的历史数据对2010-2012年和2010-2014年的固定资产投资进行事后预测，前者代表短期预测，后期代表中长期预测，并将预测值与实际值进行对比，结果表明，两种方法预测出来的结果均比实际值低，而且二次指数平滑法预测的误差过大，预测精度过低，ARIMA模型的预测精度相对较高，但两种方法都出现中长期预测的误差变大的问题。这个检验结果也表明了，在政策有较大变动或者政策频繁变动时期，固定资产投资的预测精度会下降，随着预测期的加长，预测值的质量更是明显下滑。利用福建省1980-2014年固定资产投资额，运用ARIMA(4,2,4)模型与二次指数平滑法(平滑系数为0.8)对福建省2015-2017年固定资产投资进行预测，结果仍然是ARIMA模型的预测值大于二次指数平滑法的预测值，结合未来福建省固定资产投资增速放缓的估计，对两种方法的预测值取平均值，得出预测结果为2015年固定资产投资额20978.51亿元，2016年为24313.01亿元，2017年为28012.12亿元。

注释：

① 本文所用数据来自1980-2013年的福建省统计年鉴和2014年福建省统计公报。

参考文献：

[1]石美娟．ARIMA模型在上海市全社会固定资产投资预测中的应用[J].数理统计与管理，2005，(1)：69～74.

[2]蒋燕．ARIMA模型在广西全社会固定资产投资预测中的应用[J].数理统计与管理，2006，(5)：588～592.

[3]王新华．ARIMA模型在武汉市全社会固定资产投资预测中的应用[J].统计与决策，2006，(8)：84～85.

[4]刘爱萍，郜文明．ARIMA模型在省级全社会固定资产投资预测中的应用[J].河南金融管理干部学院学报，2008，(4)：105～107.

[5]艾洪德．基于“保增长”目标的辽宁固定资产投资预测研究[J].财经问题研究，2009，(7)：64～71.

[6]黄宝如，李斌．固定资产投资预测的Logistic模型及实证分析[J].同济大学学报：自然科学版，2005，(2)：251～254.

[7]徐志勇，秦伟良，李奇送．江苏省全社会固定资产投资预测[J].安徽农业科学 ，2007，(5)：1551～1553.

[8]陈悦华，廖造壮．基于灰色理论的武汉市全社会固定资产投资预测[J].科学技术与工程，2012，(5)：36～38.

[9]王晓辉，范德成．基于人工神经网络的我国固定资产投资预测研究[J].现代管理科学，2009，(1)：74～75.

[10]詹英．组合预测方法在我国人均GDP预测中的应用[D].武汉：华中师范大学，2014.

[11]易丹辉．数据分析与EViews运用(第二版)[M].北京：中国人民大学出版社，2014.

Study on the Investment Forecast of Social Fixed Assets

in Fujian Province: Based on the Application of ARIMA

Model and Second Exponential Smoothing Method

LIN Ya-na，HUANG Xian-jun

(College of Economics, Fujian Agriculture and Forestry University, Fuzhou 350002,China)

Key words: ARIMA model; second exponential smoothing method; fixed asset investment

(责任编辑：杨成平)