基于CVaR的典型交易成本的投资组合模型

房成德，韦增欣，张梦颖

(广西大学数学与信息科学学院， 广西南宁530004)



基于CVaR的典型交易成本的投资组合模型

房成德，韦增欣，张梦颖

(广西大学数学与信息科学学院， 广西南宁530004)

摘要：投资者利用有限的资本在预期收益的条件下来控制风险是投资目的之一，因此假设投资者是风险厌恶型，用CVaR作为测量投资组合风险的方法。在成本约束条件下，以CVaR为目标函数，建立了带有典型交易成本函数的投资组合模型,给出了求解该模型的算法步骤。选取我国股票市场上的历史数据进行了实证分析，验证该模型的有效性。

关键词：投资组合；交易成本函数；CVaR；最优化模型

0引言

进入20世纪末以来，一些大的金融机构，如巴林银行、MGRM都因为对金融资产的风险管理和监控处理不当遭受巨额损失甚至破产，特别是2008年美国发生次贷危机以来。因此，如何处理市场上出现的风险，较准确地计算风险并且规避风险，建立完整的风险体系，一直是金融机构及其监管当局研究的重点之一。

自从1952年Markowitz[1]提出了均值—方差资产组合模型以来,越来越多的学者对投资组合理论展开了深入的研究，早期的投资组合理论的研究大多集中在离散时间条件下的各种单期和多期投资组合问题，自从Merton[2]首次提出连续时间条件下的投资组合问题以来，随着理论和计算机技术的飞速发展，连续时间条件下的投资组合问题成为了研究热点。投资组合理论大致发展为：流动性的投资组合理论[3]、基于VaR的投资组合理论[4]、行为投资组合理论[5]和基于非效用的投资组合理论[6]。虽然现代投资组合理论近年来得到了很大的发展，但是如何度量投资组合风险是本文研究的重点之一。在Markowitz的均值—方差模型中，方差作为度量风险的方法存在一些缺陷：模型的计算量大；方差不仅刻画了上半方差也反映了下半方差，而投资者最关心的风险是负收益率的波动，并且方差只是刻画了收益的波动而没有反映出投资金额的损失多少。为此，1996年Morgan[7]提出了VaR(Value-at-Risk) ,它表示在一定的置信水平下，投资组合在未来特定一段时间内的最大可能损失。VaR是一个被广泛认可并有着重要应用的风险度量指标，虽然具有很多优点，但是VaR不能度量超过本身的损失，且不满足次可加性。针对VaR的不足，Rockefellar等[8]在2000年提出了CVaR(Conditional value-at-risk),它表示在固定的投资期限和置信水平下，某一资产组合面临的损失超过VaR的平均值,而且Pflug[9]证明了CVaR满足次可加性，是一致风险度量。因此，CVaR成为一种有效的风险度量，已经被应用于解决金融市场风险管理问题。

国内外学者对成本影响投资组合模型的影响进行了大量研究，Perold等[10]将线性交易成本函数引入到投资组合模型。Dantgiz等[11]首次在投资组合模型中引入了非线性交易成本函数，国内学者王春峰等[12]首次将典型交易成本函数引入投资组合管理模型,后来，阿春香等[13]又探究了典型交易成本下的相关机会模型。

笔者在文献[12]的基础上改进了典型交易成本函数，建立了基于CVaR的含有改进的典型交易成本函数的投资组合模型[12-14]，由于建立的模型是非线性模型，传统的算法很难求解。为了更好地求解此模型，笔者考虑用杂草算法来求解新建的模型。选取我国股票市场上历史数据来进行一组数值实验，通过对数值试验结果的讨论分析，验证新模型的可行性。

1CVaR方法基本原理

设f(X, Y):Rm×Rn→R表示一个投资组合的损失函数，其中X为投资决策向量，Y为收益率随机向量。那么当X固定时，f(X, Y)是关于Y的函数，假设Y为连续型随机变量，Y的概率密度函数为P(Y)而且连续，则当Y的分布已知时，损失函数f(X, Y)为依赖X的随机变量，则它不超过某一持有水平α的概率为:

φ(X,α)=∫f(X,Y)≤αP(Y)dY。

(1)

显然φ(X,α)是关于α的非增且右连续函数，假设用β表示置信水平(0≤β≤1)，则以β为置信水平的关于X的VaR和CVaR可表示为:

VaRβ(X)=min{α∈R:φ(X,α)≥β}。

(2)

根据CVaR的定义：CVaR是指在给定期限和置信水平下，某一资产组合面临的损失超过VaR的平均损失，则投资组合的CVaR可以表示为：

CVaRβ(X)=E{f(X,Y)≥VaRβ(X)}=(1-β)-1∫f(X,Y)≥VaRβ(X)f(X,Y)P(Y)dY。

(3)

从CVaR的计算可以看到，CVaR的计算里面包含VaR的函数，很难通过定义来直接计算和优化CVaR。因此，Rockafellar构造了辅助函数Fβ(X,α)将CVaR和VaR联系起来[8],辅助函数表示为：

Fβ(X,α)=α+(1-β)-1∫Y∈Rn[f(X,Y)-α]+P(Y)dY,

(4)

其中：[f(x,y)-α]+=max{f(x,y)-α,0} 此时CVaRβ(X)=minFβ(X,α)。

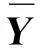
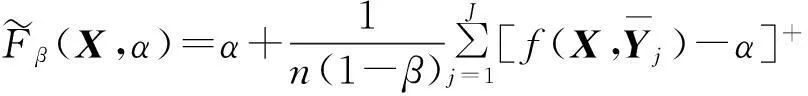
(5)

2基于CVaR的含有改进的典型交易成本函数的投资组合模型

假设投资者投资市场上n种风险资产，且投资者对这n种投资是自由的，其投资的目的是追求收益的最大，设X=(x1,x2,…,xn)为投资者对这n种风险资产的决策头寸，风险资产的期望收益率为R=(r1,r2,…,rn)，此时这里风险资产的组合收益率可以表示为：

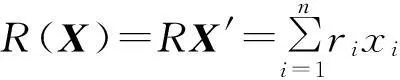
(6)

在投资组合管理中，为了实现既定的投资目标，管理者需要根据市场的变化不断调整现有的投资组合，即要进行资产交易，假设每次交易时，都需要付出相应的交易成本。通常对实际交易成本的描述具有复杂的数学形式，因此经典Markowitz投资组合管理模型忽略了交易成本，而实际上付出成本对获得的收益会产生很大的影响的，所以忽略交易成本往往会导致无效的投资组合。国内外学者对于含有交易费用的投资组合模型[10-11]进行了细致的研究，但是现实市场上的交易费用是复杂变化的，很难用上述研究中假定的交易成本来表示实际交易成本。国内学者王春峰等首次将典型交易成本函数引入投资组合管理模型[12,14]中。下面先对典型交易成本函数进行描述。

图1　典型单位交易成本函数Fig.1　Typical unit transaction cost function

通常实际交易成本函数表现为资产交易量具有两个拐点的非凸非凹的函数(如图1所示)，称之为“典型交易成本函数”。当资产交易额较小时，由于交易效率低下，所以单位交易成本很大；随着资产交易额的上升，单位交易成本将逐渐减小。故在达到A点之前，交易成本函数C(X)是凹型的。然而当越过A点后单位交易成本已经最优，于是单位交易成本将保持不变，或者说交易成本函数C(X)将随着资产交易量的增加呈线性增加，直到到达B点，即交易函数AB段是线性的。如果资产交易额继续增加，越过B点后，由于股票资产供给不足等因素使得对应的单位交易成本逐渐变大，所以交易成本函数C(X)在越过B点之后将变成凸的。则给出此时典型交易成本函数的表达式如下，记每次交易时的交易成本函数为C(X)，则有：

C(X)=(c1(x1),c2(x2),…,cn(xn)),

(7)

(8)

然而在实际的金融市场上，交易成本函数很难会出现线性增加的情况。因为随着资产交易量的增加，随之而来的宣传费，安全维护费，大型服务器建设费会相应的增加，这些因素都对AB段的单位交易成本函数产生很大的影响，所以也应将AB段视为凸的，但是又要考虑到单位成本增加的速度要弱于超过B点以后的部分(如图2所示)。因此本文给出如下改进后的典型交易成本函数的表达式如下，记每次交易时的交易成本函数为C(X)，则有：

C(X)=(c1(x1),c2(x2),…,cn(xn)),

(9)

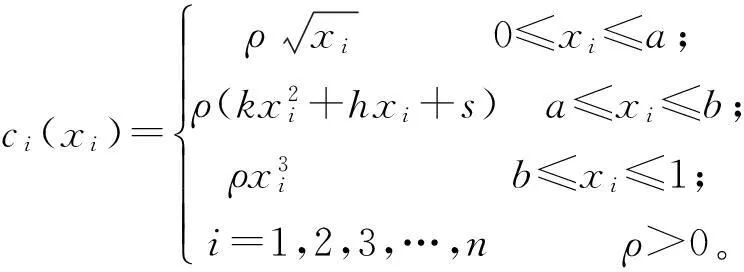
(10)

图2　改进的典型单位交易成本函数Fig.2　Improved typical unit transaction cost function

其中，k表示二次项系数，h表示一次项系数，s表示截距，ρ为大于0的参数。

综上，得到基于CVaR的含有改进的典型交易成本函数的投资组合模型如下：

(11)

其中，M表示预期的最低收益率，xi≥0表示不允许卖空，ci(xi)即为式(10)中的交易成本函数。

3求解模型的算法设计

由于新建模型中引入了改进的典型交易成本函数，考虑到模型的非线性，一般的算法很难求解该模型。为了更好的求解此模型，本文引入了杂草算法来求解。

杂草算法(invasive weed optimization，IWO)是Mehrabian等[15]在2006年最早提出的。 杂草算法是一种受杂草启发而提出的，基于种群的数值优化计算方法。IWO算法具有算法结构简单、参数少、鲁棒性强、收敛快等特点，已经被应用于许多领域,IWO算法是一种受杂草启发而提出的新型智能优化算法，其执行过程是模拟杂草入侵的过程。IWO算法的基本流程包含以下步骤：

Step 1: 种群初始化。IWO算法是一种基于种群的数值优化计算方法，在优化迭代之前，需要确定初始杂草种群规模N和最大杂草种群规模Nmax,问题维数D,最大迭代次数Kmax,然后随机产生N个杂草个体作为初始解。

Step 2: 生长繁殖。每个杂草根据适应性(繁殖能力)产生种子，适应度好的个体具有较强的繁殖能力，适应度差的个体繁殖能力也较差。杂草个体q产生的种子个数公式为:

(12)

其中，f为当前杂草个体q的适应度值，fmax为当前杂草个体q的最大适应度值，fmin为当前杂草个体q的最小适应度值，smax,smin分别为一个杂草能产生的最大和最小种子个数，为可调参数。

Step 3: 子代分布。以父代为均值，子代杂草个体以正态分布方式扩散于父代周围。迭代过程中，每一代的标准差σ按下式进行变化：

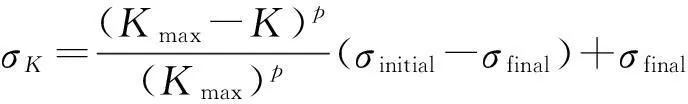
(13)

其中，σK为当前的标准差值，K为当前的进化代数，σinitial,σfinal分别为起始和最终的标准差值，p为非线性调和指数，一般情况下取p=3。

Step 4: 生存竞争。在杂草进化过程中，当杂草个体达到最大杂草种群规模时，则对所有杂草个体按照适应度值大小进行排序，取适应度值最优的Nmax个杂草个体，淘汰其余的个体，并将选取的Nmax个杂草个体返回step 2进行新一轮进化。

4数值算例

本文建立了一种基于CVaR的含有改进的典型交易成本函数的投资组合模型，并且给出了求解该模型的算法即杂草算法。为了验证新模型和算法的可行性和有效性，现选取市场上10只股票作为风险资产，即n=10，这10只股票分别为：白云机场(600004)、皖通高速(600012)、丹化科技(600844)、天津松江(600225)、日照港(600017)、传化股份(002010)、赛象科技(002337)、惠而浦(600983)、航民股份(600987)、麦迪电气(300341)。利用Matlab软件对数据进行处理，通过设置不同的预期收益率M,得到10只股票的投资权重和风险值,如表1。

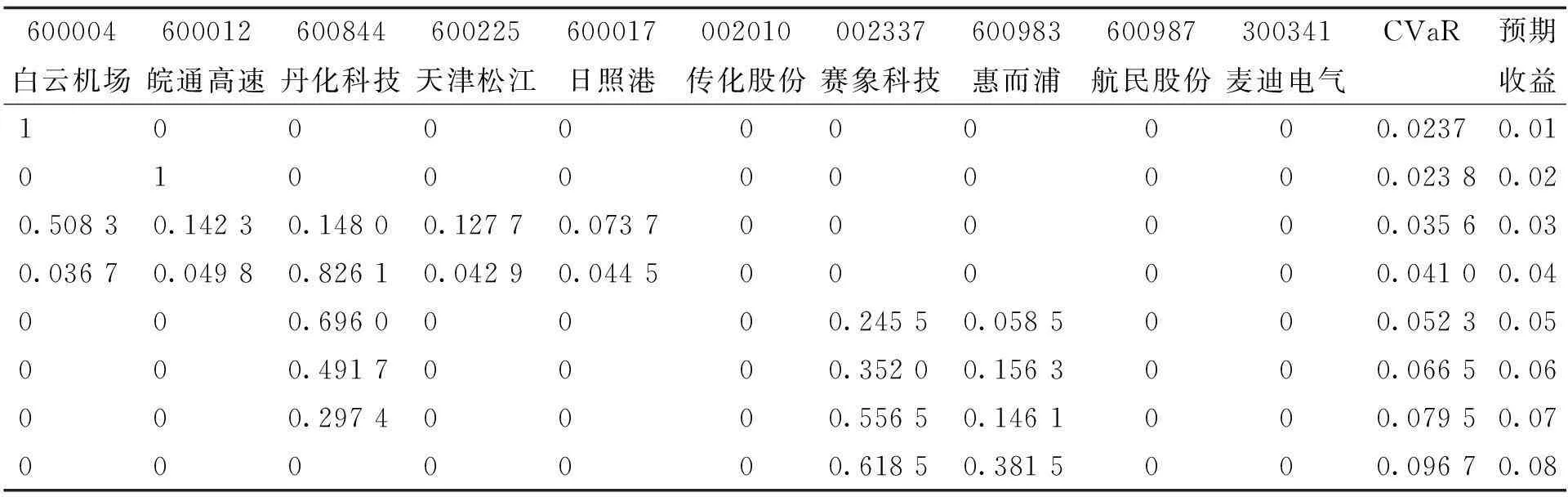
表1　10只股票的预期收益、风险与投资比例

从表1可知：

①投资组合的风险CVaR与投资组合预期收益成正相关，即投资组合的风险值CVaR随预期收益的增大而增大。当预期收益从0.07增加到0.08时，投资组合风险值CVaR从0.079 5增加到0.096 7；

②若投资者想要获得更高的预期收益，则需要增加对赛象科技(002337)和惠而浦(600983)的投资比重，由此也将导致资产组合的高风险。因此，投资者应该综合考虑自身的收益和风险承受的能力，设定符合自己的预期收益值。

③在一定的预期收益内，随着预期收益的变化，投资组合的风险几乎不发生变化，所以投资者需要设定一个最低的收益水平，在保证最低收益的基础上，优化资产配置来获得更大的收益。

5结语

本文是在典型交易成本函数的投资组合模型的基础上，改进了典型交易成本函数，建立了基于CVaR的含有改进的典型交易成本函数的投资组合模型，并给出了求解此非线性模型的杂草算法步骤，最后进行了实证研究.通过研究发现新建的模型可以说明投资组合收益与风险之间的关系，为投资者决策提供了重要依据。

参考文献:

[1]MARKOWITZ H.Portfolio selection[J]. The journal of finance, 1952, 7(1): 77-91.

[2]MERTON R C.Optimum consumption and portfolio rules in a continuous-time model[J]. Journal of Economic Theory, 1971, 3(4): 373-413.

[3]LONGSTAFF F A.Optimal portfolio choice and the valuation of illiquid securities[J]. Review of financial studies, 2001, 14(2): 407-431.

[4]EMBRECHTS P, MCNEIL A, STRAUMANN D.Correlation and dependence in risk management: properties and pitfalls[J]. Risk management: value at risk and beyond, 2002,29(3): 176-223.

[5]SHEFRIN H, STATMAN M.Behavioral portfolio theory[J]. Journal of financial and quantitative analysis, 2000, 35(2): 127-151.

[6]KORN R.Value preserving portfolio strategies in continuous-time models[J]. Mathematical methods of operations research, 1997, 45(1): 1-43.

[7]JORION P. Value at Risk: the benchmark for controlling market risk.[S.l.][J]. Chicago: Irwin Professional, 2000,14(2):47-56.

[8]ROCKAFELLAR R T, URYASEV S.Optimization of conditional value-at-risk[J]. Journal of risk, 2000(2): 21-42.

[9]PFLUG G C.Some remarks on the value-at-risk and the conditional value-at-risk [M]. USA: Probabilistic Constrained Optimization, 2000: 272-281.

[10]MULVEY J M, VLADIMIROU H.Stochastic network programming for financial planning problems[J]. Management Science, 1992, 38(11): 1642-1664.

[11]DANTZIG G B, INFANGER G.Multi-stage stochastic linear programs for portfolio optimization[J]. Annals of Operations Research, 1993, 45(1): 59-76.

[12]王春峰,杨建林,赵欣.具有典型交易成本的投资组合管理模型及其求解[J]. 系统工程理论与实践, 2002,22(10): 134-138.

[13]阿春香, 刘三阳.具有典型交易成本的组合投资问题的相关机会模型[J]. 应用数学, 2007 (S1): 105-110.

[14]李晓清, 宋江泽, 韦增欣.带有改进的典型交易成本函数的 MCvar 模型及其例证分析[J]. 数学的实践与认识, 2014, 13: 014.

[15]MEHRABIAN A R, LUCAS C.A novel numerical optimization algorithm inspired from weed colonization[J]. Ecological informatics, 2006, 1(4): 355-366.

(责任编辑梁碧芬)

The portfolio model with typical transaction cost based on CVaR

FANG Cheng-de， WEI Zhen-xin, ZHANG Meng-ying

(College of Mathematics and Information Science, Guangxi University, Nanning 530004,China)

Abstract:The use of limited capital to control risk under the expected return condition is one of the purpose of investment, assuming that investors are risk averse. CVaR was used as a method to measure a portfolio risk.A portfolio model with typical transaction cost was constructed under the cost constraint condition and the CVaR as an objective function, and the algorithm steps of solving the model are provided.The empirical analysis of the historical data of China’s stock market is carried out to verify the validity of the model.

Key words:investment portfolio ; transaction cost function; CVaR; optimization model

中图分类号：F837.12;F835;F224

文献标识码：A

文章编号：1001-7445(2015)06-1611-06

doi:10.13624/j.cnki.issn.1001-7445.2015.1611

通讯作者：韦增欣(1962—)，男，广西武鸣人，广西大学教授，博士生导师；E-mail:zxwei@gxu.edu.cn。

基金项目：国家自然科学基金资助项目(11161003)

收稿日期：2015-09-02；

修订日期：2015-10-03