求解非线性对称方程组的范数下降算法

王晓亮,袁功林,段侠彬,崔曾如,盛　洲

(广西大学数学与信息科学学院, 广西南宁530004)



求解非线性对称方程组的范数下降算法

王晓亮,袁功林,段侠彬,崔曾如,盛洲

(广西大学数学与信息科学学院, 广西南宁530004)

摘要：针对非线性对称方程组求解问题，提出了一种具有回溯线搜索技术的修正方法，该方法不仅具有下降性质而且在适当的条件下具有全局收敛性。数值结果表明该算法对非线性方程组问题是有效的。

关键词：回溯线搜索技术;非线性方程组;下降性;全局收敛性

0引言

考虑下面的非线性方程组：

F(x)=0,x∈Rn,

(1)

其中F: Rn→Rn是连续可微的，且它的雅克比矩阵F(x)在x∈Rn是对称的。令‖F(x)‖2为一范数函数，则非线性方程组问题(1)等价于下面的优化问题:

minθ(x),x∈Rn。

(2)

求解非线性方程组问题的方法有多种，一种常见的方法是迭代法，在本文，笔者利用迭代线搜索技术来求解问题(1)，其一般迭代公式为：

xk+1=xk+αkdk,

(3)

其中dk是线搜索方向，αk是沿着dk的步长。求解步长αk和方向dk的方法有很多种(见文献[1]~文献[14]),在给出新算法之前，笔者先介绍一种常见的求步长αk和方向dk的方法。

鲁习文等[4]提出了一种修正的单调下降线搜索技术：

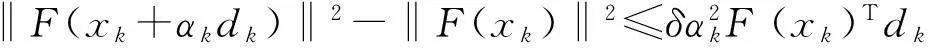
(4)

其中δ∈(0，1),αk=max{1,r,r2,…}且使式(4)成立。该方法在适当的条件下具有全局收敛性和超线性收敛等性质，数值结果也表明该方法比其他的一般线搜索技术更具有竞争力。

袁功林[14]提出了一种新的搜索方向：

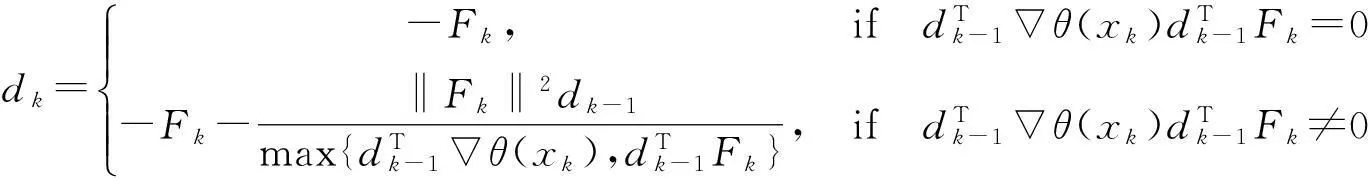
(5)

其对范数函数θ(x)具有独立于线搜索的下降性；在适当的条件下，该方法比BFGS方法有更好的数据表现。

笔者基于文献[14]的思想，提出了一个改进的搜索方向技术，并且在适当的条件下证明了其全局收敛性等性质。贯穿本文，‖‖表示欧式范数，Fk和Fk+1分别是F(xk)和F(xk+1)的简写，序列{xk}是由算法产生的迭代点列。

1算法

在计算步长αk时，雅可比矩阵F(x)的计算会明显的增加计算量和消耗更多的时间。为了避免该缺陷，在本文，笔者将利用线搜索式(4)来求解步长αk。

文献[14]提出了一个新的搜索方向如式(5)，它对范数函数θ(x)具有独立于线搜索的下降性。受此启发，笔者给出一个修改的线搜索方向：

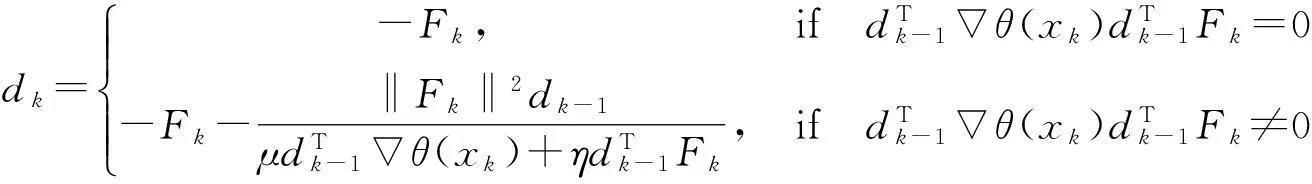
(6)

其中μ，η≥1。

算法MYL步骤如下：

Step 0： 给定x0∈Rn，常数η，μ；r,δ∈(0,1)，τ,ε∈(0,1)。令k:=1。

Step 1： 如果‖Fk‖<ε，则停止；否则进行step 2。

Step 2： 通过式(6)计算搜索方向dk。

Step 3： 若 ‖F(xk+dk)‖≤τ‖F(xk)‖，则αk=1，转入step5；否则转入step4。

Step 4： 令ik是使式(4)成立的最小的非负整数，则αk=rik；

Step 5： 利用迭代公式xk+1=xk+αkdk，计算新的迭代点xk+1。

Step 6： 如果‖Fk+1‖<ε，则停止，否则令k=k+1，返回step2。

2全局收敛性

令Ω为一水平集，它的定义为：

Ω={x|‖F(x)‖≤‖F(x0)‖}，

为了得到算法MYL的全局收敛性，本文做如下假设：

假设1：F在包含于Ω的一个开凸集Ω1上是连续可微的。

假设2：F的雅可比矩阵在集合Ω1上是对称的、有界的、正定的，即存在正的常数M≥m>0使的对任意的x∈Ω1，d∈Rn都有:

‖F(x)‖≤M和m‖d‖2≤dTF(x)d≤M‖d‖2,

(7)

成立。

②由假设1和假设2对任意的d∈Rn，x,y∈Ω1，有如下结论：

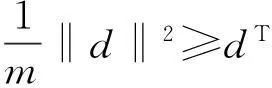
(8)

M‖d‖≥‖F(x)d‖≥m‖d‖和M‖x-y‖≥‖F(x)-F(y)‖≥m‖x-y‖。

(9)

下面的引理表明了由式(6)定义新的搜索方向对范数函数θ(x)具有独立于线搜索的下降性。

引理1若假设1和假设2满足， 则存在正常数n1,n2使得对任意k≥0，都有：

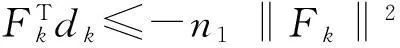
和

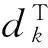
成立。

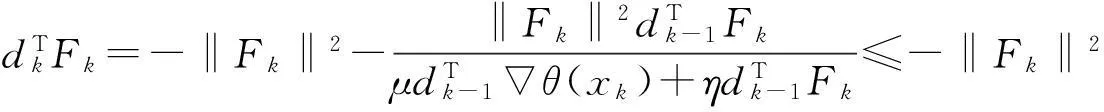
其中不等式可以从注①中得到。

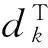
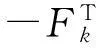
(10)

其中最后一个不等式由式(8)得到。综上所述，取n1∈(0,1)和n2∈(0,1/M)，则引理得证。

通过上面的引理，可以得出范数函数θ(x)沿着搜索方向dk是下降的，这意味着对所有k≥0，都有‖Fk+1‖≤‖Fk‖成立。与文献[4]中引理3.2相似，可以得到下面的引理，这里省略其证明。

引理2 若假设1和假设2成立，{αk,dk,xk,Fk}由算法MYL产生，则序列{xk}⊂Ω，并且序列{‖Fk‖}收敛。

引理3若假设1和假设2成立，{αk,dk,xk,Fk}由算法MYL产生，则有：

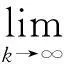
(11)

证明：由式(4)， 则：

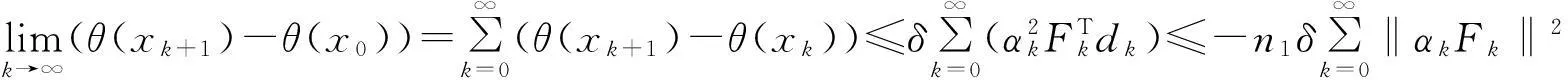
由序列{θ(xk)}是严格下降的，故引理得证。

下面将证明在满足假设1和假设2的情况下，算法MYL的全局收敛性，即存在序列{xk}的一个聚点，其是方程公式(2)的一个稳定点，即满足：

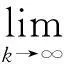
(12)

定理1若假设1和假设2满足，{αk,dk,xk,Fk}由算法MYL产生，则式(12)成立。

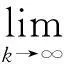
(13)

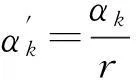
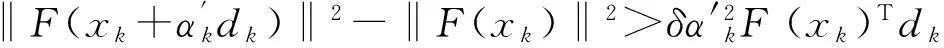
(14)

。

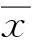
(15)

另一方面，在不等式(10)两边同时对k取极限，则得到：

。

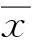
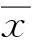
3数值结果

将对算法MYL和BFGS算法的数值表现进行测试、比较。为了避免计算范数函数θ(x)的雅可比矩阵θ(x)，在数值试验中用‖Fk+1‖-‖Fk‖来代替θ(xk+1)。具有固定初始点的测试函数(见文献[11],文献[14]~文献[16])如表1，其中：

F(x)=(f1(x),f2(x),…,fn(x))T。

表1　测试函数

试验时，所有的代码都在MatlabR2010b 上进行编写，程序在CPU为Intel Pentium(R)Dual-Core E5800 3.20 GHz， SDRAM为2.00G bytes的Windows 7操作系统下运行。在试验中，算法中的参数的选择为μ=1，η=1，r=δ=0.1，τ=0.5，ε=10-5。试验终止的条件为‖F(x)‖≤10-5或者NI≥1 000。试验结果见表2，其中的元素有下列的定义：

Dim：问题的维数； NI: 试验中迭代次数；NF：试验中函数值计算次数；GN：当试验终止时，F(x)的范数‖F(x)‖；Cputime：试验所需时间,s；fail：试验失败。

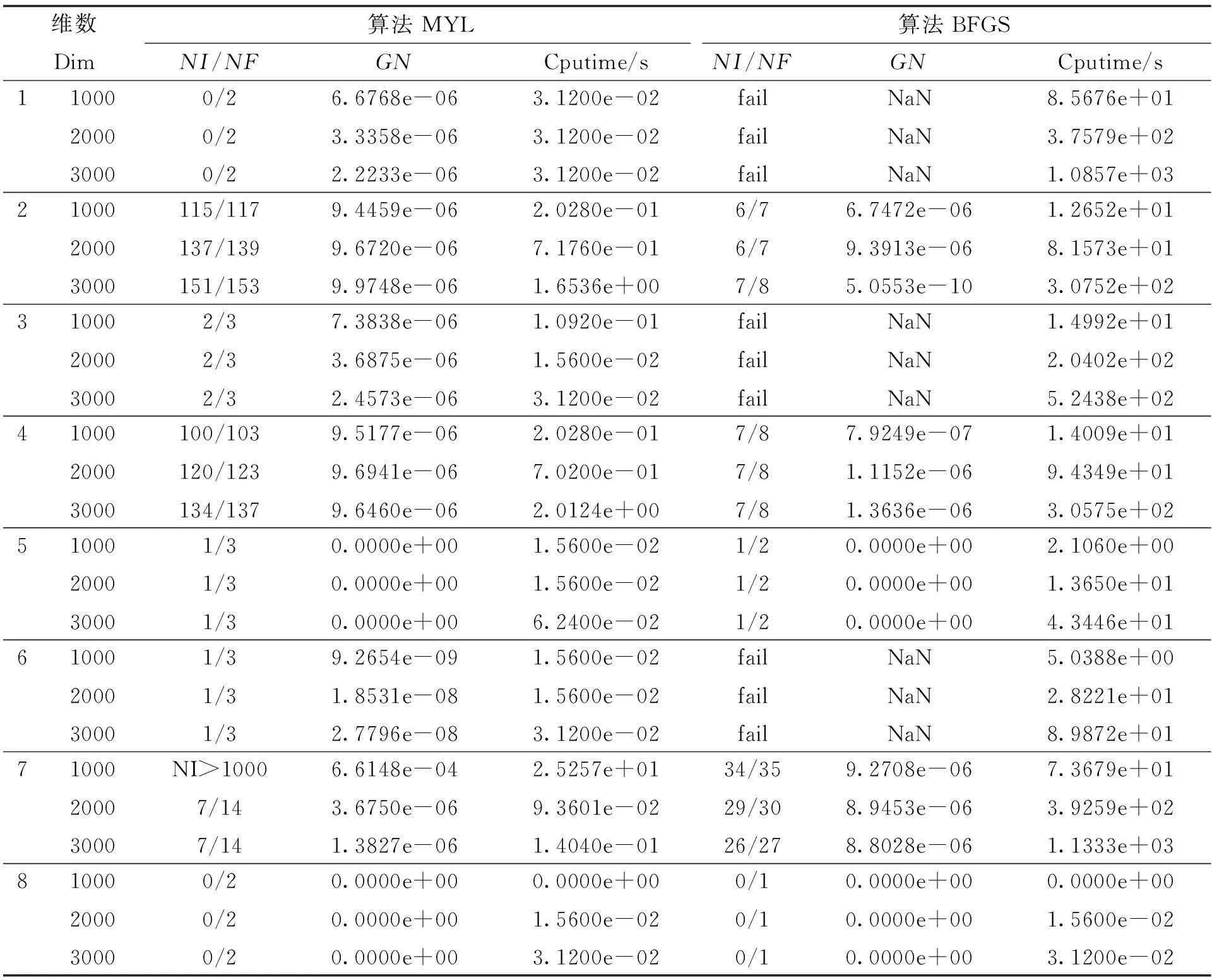
表2　数值结果

从表2不难发现算法MYL在解决非线性方程组问题方面比一般的BFGS方法更有效:对于问题1，3，6，一般的BFGS方法不能求解，而的算法MYL可以十分有效的快速解决。对于问题7在Dim=1 000时，算法MYL 因迭代次数超过1 000而失效；同时还可以看到，一般的BFGS方法对上述8个问题进行求解时，其消耗的时间都不少于算法MYL求解时所需时间。因此，算法MYL是合适的。

4结语

对于求解非线性对称方程组问题，本文基于文献[14]的思想，提出了一个改进的搜索方向技术。在适当的条件下，建立了算法MYL的下降性、全局收敛性和局部收敛性等性质。在数值试验中，可以发现算法MYL比一般的BFGS方法在求解非线性对称方程组问题中耗费的时间更短，而且可以求解的问题更多。因此，算法MYL是有效的。

参考文献:

[1]ZHU D.Nonmonotone backtracking inexact quasi-Newton algorithms for solving smooth nonlinear equations[J]. Applied Mathematics and Computation, 2005, 161(3): 875-895.

[2]LI D, FUKUSHIMA M.A global and superlinear convergent Gauss-Newton-based BFGS method for symmetric nonlinear equations[J]. SIAM J.Numer.Anal.1999,37:152-172.

[3]GU G Z, LI D H, QI L, et al.Descent directions of quasi-Newton methods for symmetric nonlinear equations[J]. SIAM Journal on Numerical Analysis, 2002, 40(5): 1763-1774.

[4]YUAN G, LU X.A new backtracking inexact BFGS method for symmetric nonlinear equations[J]. Computers & Mathematics with Applications, 2008, 55(1): 116-129.

[5]NASH S G.A survey of truncated-Newton methods[J]. Journal of Computational and Applied Mathematics, 2000,124(1): 45-59.

[6]BROWN P N, SAAD Y.Convergence theory of nonlinear Newton-Krylov algorithms[J]. SIAM Journal on Optimization, 1994, 4(2): 297-330.

[7]吴锋,李秀梅,朱旭辉,等.最速下降法的若干重要改进[J]. 广西大学学报: 自然科学版, 2010,35(4):596-600.

[8]韦增欣, 谢品杰.修改 Broyden 族在一类非精确线搜索下的全局收敛性[J]. 广西科学, 2006, 13(1): 12-16.

[9]LI Q, LI D H.A class of derivative-free methods for large-scale nonlinear monotone equations[J]. IMA journal of numerical analysis, 2011, 31(4): 1625-1635.

[10]YU Z, LIN J, SUN J, et al.Spectral gradient projection method for monotone nonlinear equations with convex constraints[J]. Applied numerical mathematics, 2009, 59(10): 2416-2423.

[11]LI X, WANG X, DUAN X.A Limited memory bfgs method for solving large-scale symmetric nonlinear equations[C]//Abstract and Applied Analysis. London: Hindawi Publishing Corporation, 2014.

[12]YUAN G. A new method with descent property for symmetric nonlinear equations[J]. Numerical functional analysis and optimization, 2010, 31(8): 974-987.

[13]SHI Z J.Convergence of line search methods for unconstrained optimization[J]. Applied Mathematics and Computation, 2004, 157(2): 393-405.

[14]RAYDAN M.The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem[J]. SIAM Journal on Optimization, 1997, 7(1): 26-33.

[15]BING Y, LIN G.An efficient implementation of Merrill’s method for sparse or partially separable systems of nonlinear equations[J]. SIAM Journal on Optimization, 1991, 1(2): 206-221.

[16]ROBERTS S M, SHIPMAN J S.On the closed form solution of Troesch’s problem[J]. Journal of Computational Physics, 1976, 21(3): 291-304.

(责任编辑梁碧芬)

A norm descent method for symmetric nonlinear equations

WANG Xiao-liang, YUAN Gong-lin, DUAN Xia-bin, CUI Zeng-ru, SHENG Zhou

(College of Mathematics and Information Science, Guangxi University, Nanning 530004, China)

Abstract:In this paper, a modified search direction with backtracking line search method for symmetric nonlinear equations is presented .Furthermore, the proposed method not only possesses descent property but also owns global convergence in mild conditions.The numerical results indicate that the presented method is effective for the given problems.

Key words:backtracking line search; nonlinear equations; descent property; global convergence

中图分类号:O224

文献标识码:A

文章编号：1001-7445(2015)06-1597-06

doi:10.13624/j.cnki.issn.1001-7445.2015.1597

通讯作者：袁功林(1976—)，河南商丘人，广西大学教授，博士生导师; E-mail：yuangl0417@126.com。

基金项目：国家自然科学基金资助项目(11261006)；广西杰出青年科学基金资助项目(2015GXNSFGA139001)

收稿日期：2015-09-20；

修订日期：2015-10-11