基于RBF神经网络的FSC赛车转向梯形断开点优化
吴 平,唐 岚,乔旭强
(西华大学汽车与交通学院, 四川成都610039)
基于RBF神经网络的FSC赛车转向梯形断开点优化
吴平,唐岚,乔旭强
(西华大学汽车与交通学院, 四川成都610039)
摘要:为了增强FSC(Formula Student China)赛车过弯时的响应和操纵稳定性,提出一种由RBF(radius basis function)神经网络进行转向梯形断开点优化的方法。首先在Adams/car虚拟样机模型中用insight模块获取64组转向梯形断开点的原始数据,然后应用原始数据对RBF神经网络进行训练,用训练好的网络优化断开点。将优化断开点代入Adams/car模型中与CarSim赛车模型进行不足转向梯度试验和方向盘角阶跃试验对比仿真。仿真结果显示,优化后的横摆角速度峰值、稳态横摆角速度和调整时间分别降低2.13%,2.07%,16.44%,不足转向梯度值最大减少0.1 deg/g。与此同时对实车前轮反向跳动工况进行K&C台架试验,对前束角变化值进行测定。在相同轮心垂直位移为±15 mm工况下,实车试验、优化后、优化前前束角变化值分别为0.02°,0.017°,0.114°,优化后前束角变化量降低85.1%。仿真和试验结果均表明,该方法有较高的可信度,提升了赛车过弯时的响应和操纵稳定性,为断开点量化设计提供一种方法。
关键词:FSC赛车;转向梯形断开点;前束角;RBF神经网络;K&C试验
0前言
中国大学生方程式汽车大赛(FSC)旨在由各大学车队的本科生和研究生构想、设计、制造、开发完成一辆小型方程式赛车并参加比赛[1]。为了提升FSC方程式赛车过弯时的响应和操纵稳定性,特对转向系统的转向梯形断开点进行设计并优化,断开点的优化方向为轮胎反向跳动时前束角的变化。前轮前束角通过改变车辆在过弯时内外轮之间的转角关系而改变车辆的转向特性,进而改变车辆的操稳性,因此前束角的变化对操稳性有着显著的影响[2]。近年来断开点优化设计主要采用遗传算法、响应面法、模拟退火算法、Adams insight优化法、空间运动学算法、R-W分析法、MATLAB 优化工具箱等优化算法,优化目标为100%阿克曼转向曲线或轮胎跳动时前束角变化值。SIMIONESCU P A等[3]国外研究者以转向阿克曼误差为目标,运用机械空间运动学函数对转向梯形进行建模分析。国内研究者中有以平面梯形为基础联合MATLAB、作图法、考虑轮胎特性等进行断开点优化[4-6],这类方法忽略了断开点Z坐标影响将会使得车轮跳动时前束角变化较大。在使用Adams进行空间梯形断开点设计中,有使用insight模块直接进行优化[7-9],有联合MATLAB设立优化目标函数对全局或局部进行优化再得到最优解[10-13],优化目标为前束角变化和阿克曼误差,其目的在于获取理想转向特性从而减缓轮胎磨损,缺少对车辆动态特性进行仿真分析。对于不同形式的转向梯形布置没有普遍意义,而且在insight中要得到理想结果将会耗费大量的时间和计算机资源。本文使用RBF神经网络对断开点进行优化。将优化断开点代入Adams/car模型中与CarSim赛车模型进行不足转向梯度试验和方向盘角阶跃试验对比仿真。同时为了验证仿真可信度,使用K&C试验台进行对比试验。
1转向梯形断开点原始数据获取
Adams模型为我校某届FSC方程式赛车原型。在该模型中,采用Adams insight模块进行原始数据生成。对于静态转向系统的分析选择求解Opposite Wheel Travel(转向轮反向跳动),轮胎跳动量设置为15 mm。在insight中以Tierod_inner(断开点内点)xi,yi,zi和Tierod_outer(断开点外点)x0,y0,z0为变量。变量个数总共为6个,每个变量设置其边界区间为2个值,总共计算结果为26=64组。这64组数据中包括断开点内外点6个坐标和对应于每一组断开点在进行轮胎跳动时前束角的最大值和最小值。使用这64组原始数据对RBF神经网络进行训练。
2神经网络算法优化转向梯形断开点
RBF神经网络径向基神经元模型如图1所示。
图1中,X为输入训练数据,Φ(x)为神经网络中径向基函数,W为权重值,Σ为求和以后的值,b为神经网络输出层权函数,y为输出函数。RBF神经网络中Basis函数和W权重计算表达式为式(1-4)[14]。
(1)
y=wTφ,
(2)
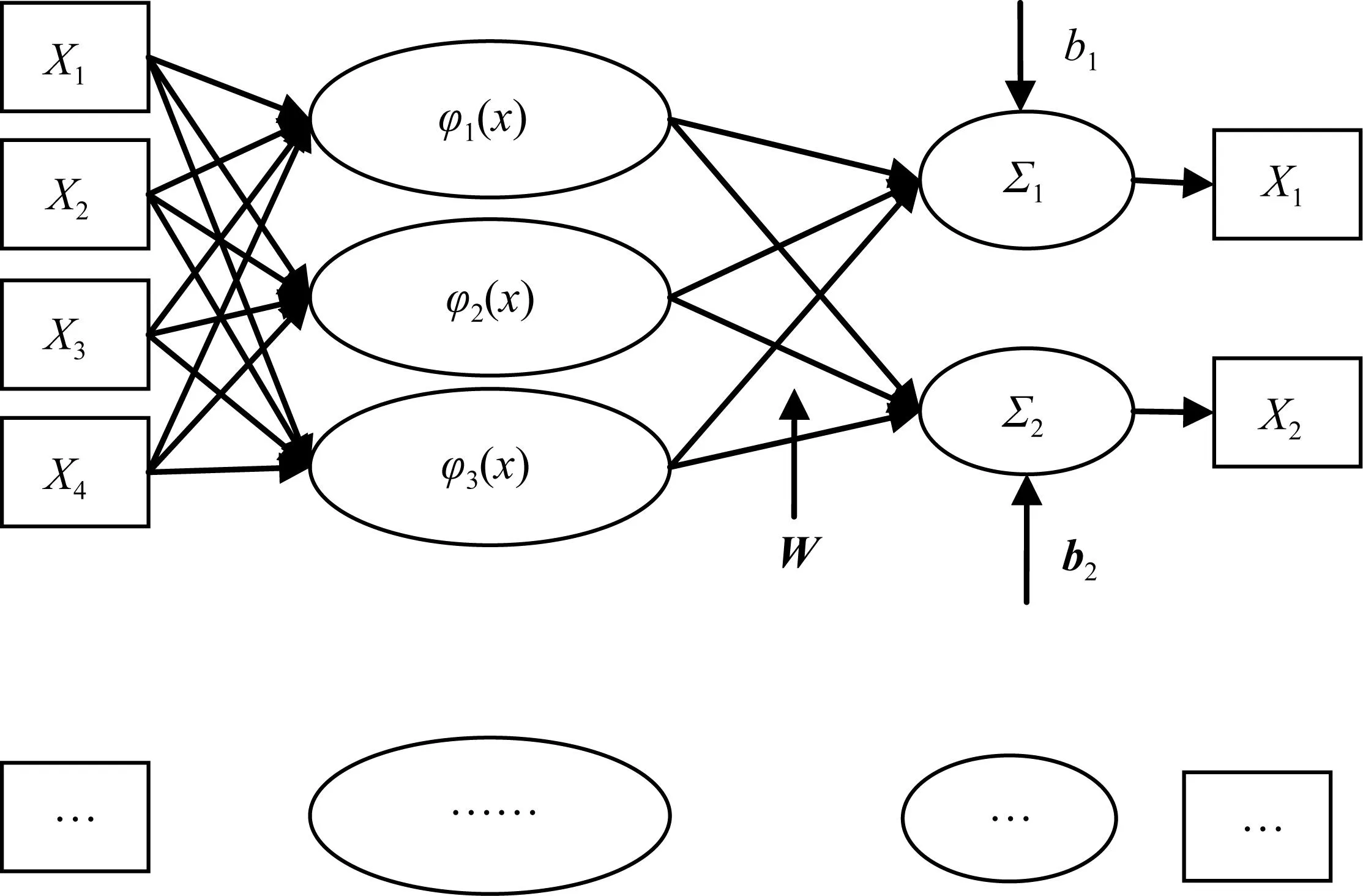
图1 径向基神经元模型
(3)
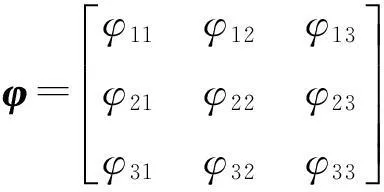
(4)
RBF神经网络Basis函数为高斯函数,其表达式为式(5-7)。
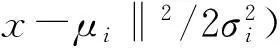
(5)

(6)
σi=1,
(7)
式中:L为输入量个数。
RBF神经网络编程使用MatlabM文件进行编写。RBF神经网络训练和优化时均以Toe_angle为输入向量,断开点坐标为输出向量。在优化输入向量Toe_angle设定为[0 0]T,其目的在于使得轮胎跳动时前束角变化量的最大值和最小值均能为0°(仿真时静态前束角设定为0°),此时RBF神经网络输出的优化值即为断开点的最优值。在对神经网络进行设置中,隐含层中神经元的初始数目通过函数式(8)进行计算。
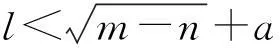
(8)

表1 神经网络设置
式中,n为输入层变量数;l为隐含层神经元数目;m为输出层变量数;a为0~10之间的常数。神经网络中所涉及参数值和RBF神经网络训练函数、误差方程、迭代步数等按照表1给定数据设置。
RBF神经网络中数据的非配情况为训练数据、验证数据、考核数据分别占总数据70%,15%,15%。为了得到优异的训练效果,需对获取的原始数据进行扩充。扩充方式为先将原数据进行复制,再将复制的数据进行顺序打乱重新排序。
RBF神经网络训练过程相关参数随迭代步数的变化情况如图2所示。从图2(a)中可以看出,在迭代步数为1 000步时搜索梯度值接近1,mu值为0.001,迭代结束时已达到最大迭代步数1 000,此时RBF神经网络训练情况比较好。从图2(b)中可以看出,训练数据、验证数据、考核数据在迭代过程中呈现下降趋势,在迭代步数为1 000时迭代结束,最优误差值接近1。
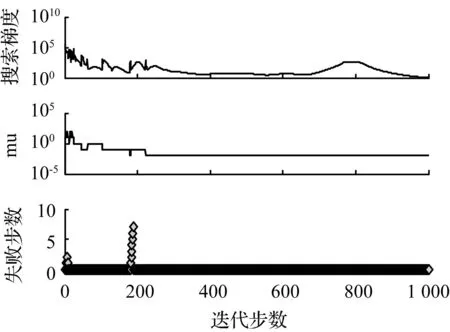
(a) 训练状态
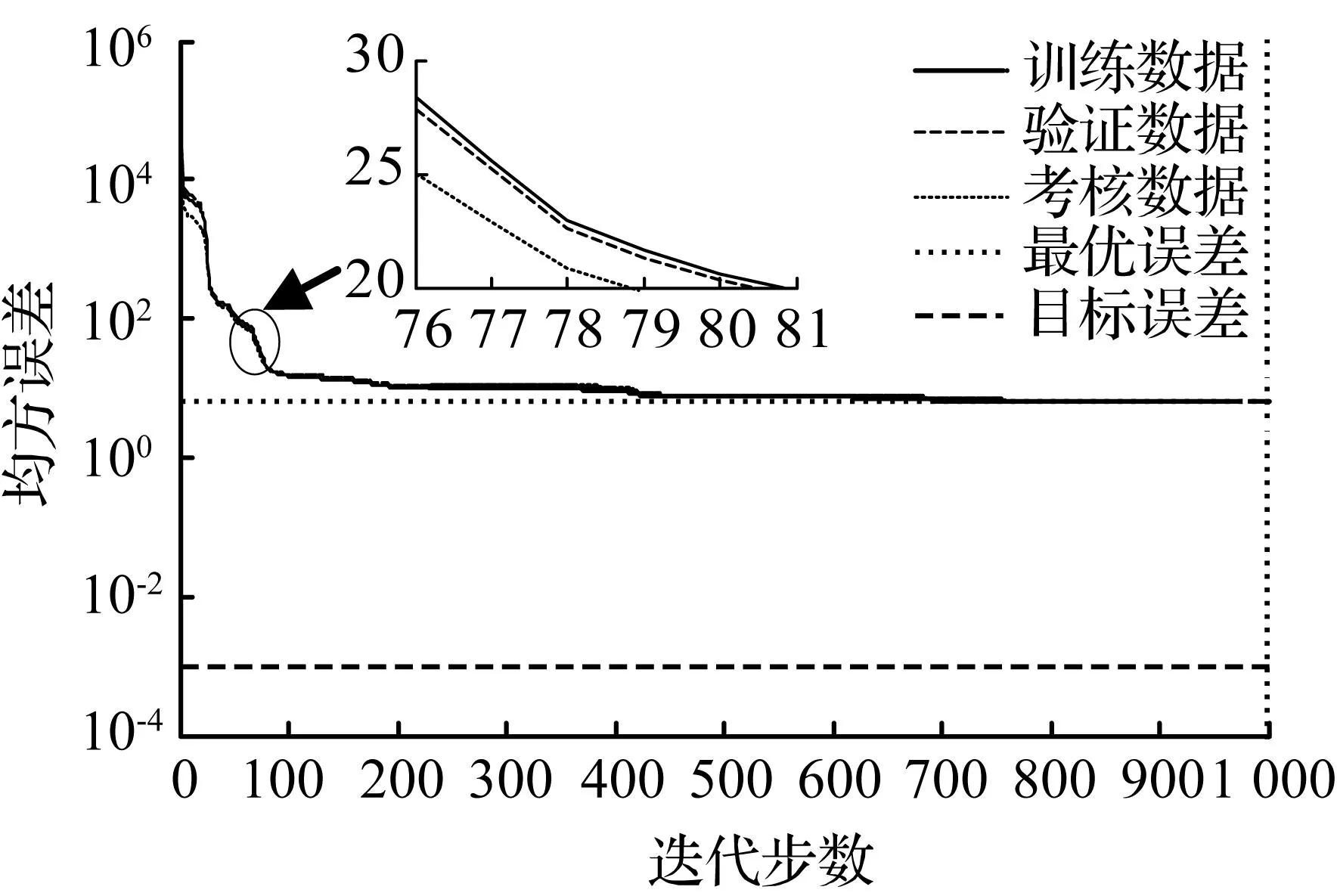
图3为均方根值误差分布直方图。从图3中可以看出,绝大部分训练数据、验证数据和考核数据的误差均集中在0误差线附近,少部分数据对称分布在0误差线两侧。说明神经网络训练情况和优化情况较好,优化点位精度较高。RBF网络在经过训练以后,将输入向量Toe_angle设定为[00]T。优化前后断开点值在表2中给出。

表2 断开点优化前后值
为了验证优化后断开点性能,将优化后的结果代入Adams模型中进行前轮反向跳动仿真,仿真结果曲线如图4。从图4中可以看出,优化前轮胎跳动±15 mm时,前束角变化值为0.114°,而相同工况下优化后变化值为0.017°,较优化前的前束角变化量降低85.1%。
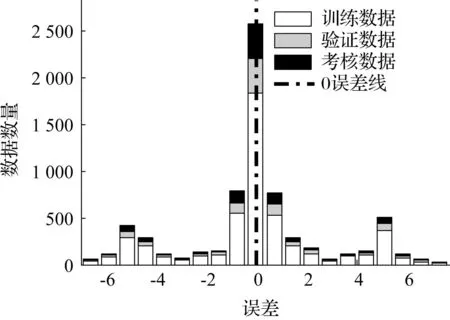
图3均方根值误差分布
Fig.3Root-mean-square value error distribution
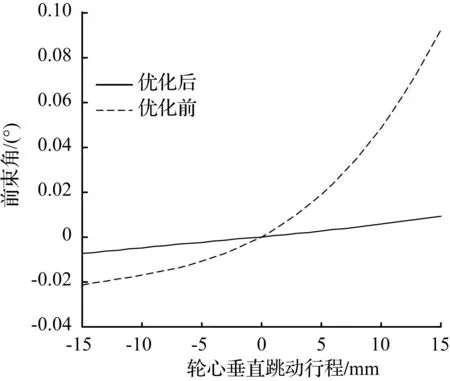
图4优化前后前束角对比
Fig.4Contrast the toe angle before
and after optimization
3Adams与CarSim对比仿真
3.1 CarSim中整车模型设置
CarSim和Adams同为车辆动力学仿真软件。CarSim是面向特性的仿真软件基于汽车动力学理论并结合多体理论。Adams是面向结构的仿真软件,基于多体动力学理论对整车拓扑结构进行抽象建模[15]。 CarSim中参数设置与Adams car中一致。
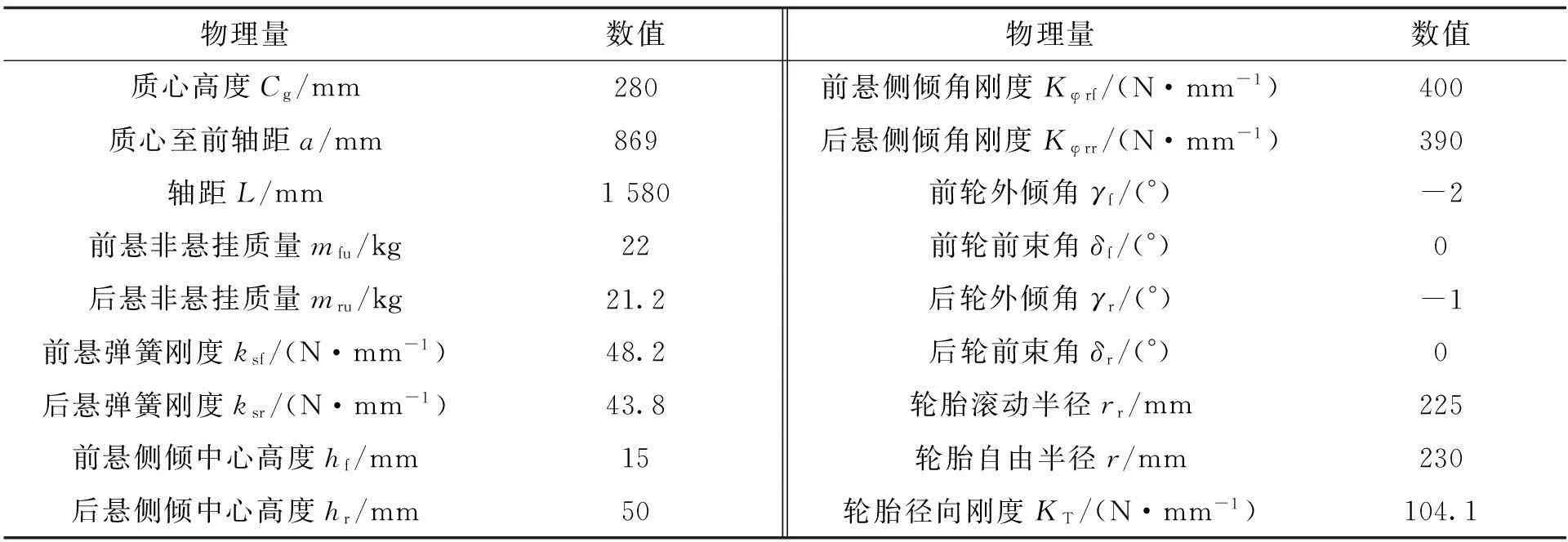
表3 CarSim中模型参数
3.2 对比仿真试验
仿真工况设定为不足转向梯度试验仿真和方向盘角阶跃试验仿真。
3.2.1不足转向梯度仿真试验
不足转向梯度表征的是不同侧向加速度与车辆转角之间的关系。试验中车辆侧向加速度值从0.1~1.6 g,半径为R=10.5 m[16-17]。试验模型为CarSim模型、Adams断开点优化后模型和Adams断开点未优化模型。不足转向梯度计算公式为公式(9)[18-20]。
K=(δ-57.3L/R)/ay,
(9)
式中:K为不足转向梯度(deg/g);ay为侧向加速度(g);L为轴距(m);R为转弯半径(m)。
3.2.2方向盘角阶跃试验
方向盘角阶跃试验目的是为获取峰值横摆角速度、稳态横摆角速度及横摆角速度响应时间。仿真车速恒定为45 km/h。测试过程中0~1 s内方向盘无转角输入,在1~1.002 s是瞬间转动方向盘30°。1.002 s以后保持该角度直到试验结束。试验模型为CarSim模型、Adams断开点优化后模型和Adams断开点未优化模型。横摆角速度计算公式为公式(10)。
γ=57.3V/R,
(10)
式中:γ为横摆角速度(deg/s);V为赛车行驶速度(m/s);R为过弯半径(m)。
3.3 仿真结果及分析
3.3.1不足转向梯度仿真试验
从不足转向梯度值仿真试验结果图5中可以看出,赛车转向特性为不足转向,在侧向加速度为0.2~0.5 g之间随着侧向加速度的增大,不足转向量在减小。大于0.5 g后不足转向梯度值基本趋于稳定。从曲线走势看,Adams与CarSim曲线走势一致,但CarSim中在较低加速度下便获得了稳定的不足转向梯度。从图6中可以看出,断开点优化后的车辆在0.1~0.6 g侧向加速度下优化后的仿真结果不足转向梯度值比未进行优化的低,更接近于中性转向。
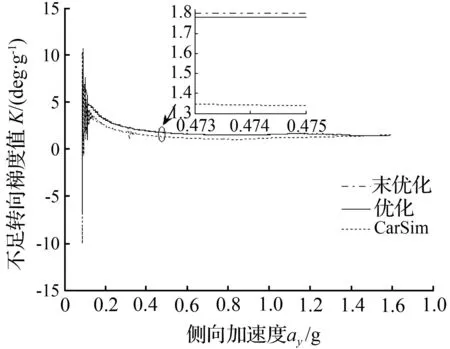
图5转向梯形断开点优化前后不足转向梯度值
Fig.5Splitting points of ackerman steering before
and after optimization understeer gradient
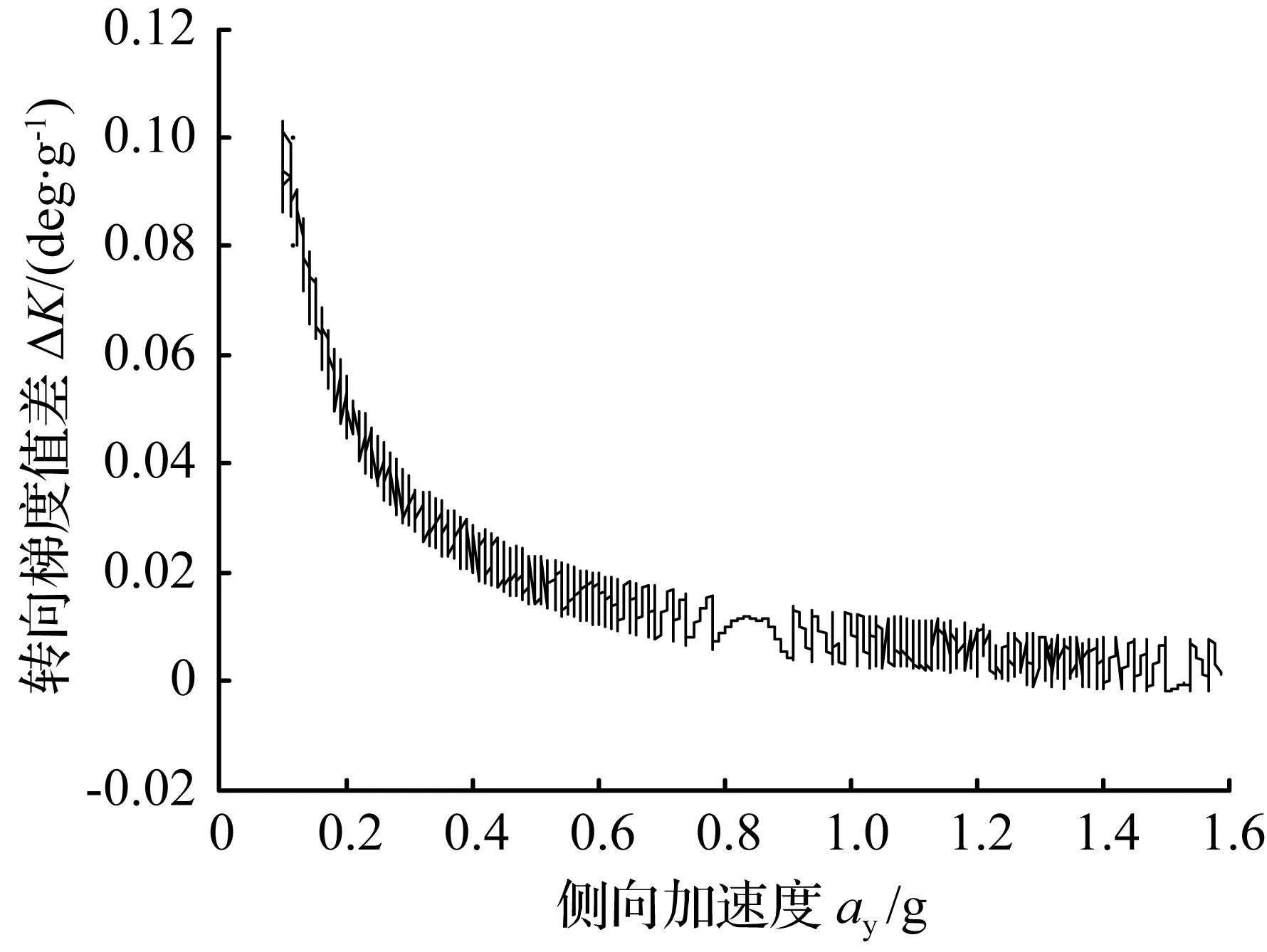
图6Adams中转向梯形断开点优化前后不足转向梯度差值
Fig.6Contrast splitting points of ackerman steering before
and after optimization understeer gradient in Adams
3.3.2方向盘角阶跃试验结果对比
图7为方向盘角阶跃试验结果。为了更好进行数据对比,提取出图7中峰值横摆角速度、稳态横摆角速度和调整时间构成表4。
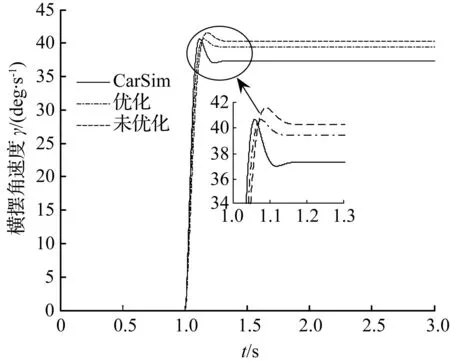
图7 优化前、优化后和CarSim横摆角速度对比

试验模型峰值横摆角速度/(deg·s-1)稳态横摆角速度/(deg·s-1)调整时间/sCarSim40.788037.35210.180Adams优化40.756639.47090.188Adams未优化41.644240.30330.225
由表4可以得出,优化后的模型横摆角速度峰值、稳态横摆角速度和调整时间相较于未优化的模型分别降低2.13%,2.07%,16.44%。Adams优化后的结果更加接近于CarSim,表明Adams仿真精度较高且可信度高。
4转向性能试验与模型验证
转向性能试验能够验证车辆模型的可信度和优化方法的可靠程度。本试验使用悬架K&C试验台架进行,主要目的是测量前束角的变化量,并将其与优化设计仿真数据进行对比从而验证模型和优化方法的可信度。K&C试验台主要由五大部分组成:车身固定系统、车轮悬架加载系统、车轮定位参数测试系统、数据采集系统和控制系统[21]。将车架与试验台通过机械连接固定在一起,测试车辆在试验台上安装完成以后实车试验测试如图8所示。

图8 实车在K&C试验台上Fig.8 Racing car on the K&C test platform
K&C试验台架前束角测量原理如图9所示。XYZ定义为车辆测试平面,△ABC为等腰三角形,且边长为a。三角形三个顶点为传感器探头,探头只能沿着Y方向移动。任意时刻车轮测试平面△A′B′C′和初始位置两平面形成空间角度,该角度绕Z轴转动的角度分量就是前束角的变化量,其表达式为式(11)。
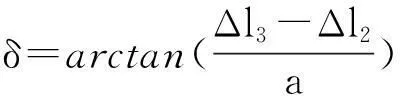
(11)
实车试验与Adams中虚拟仿真过程类似。给定轮心垂直方向位移,然后根据传感器数据解算出前束角的变化量。图10是测试根据数据绘制出的图形。
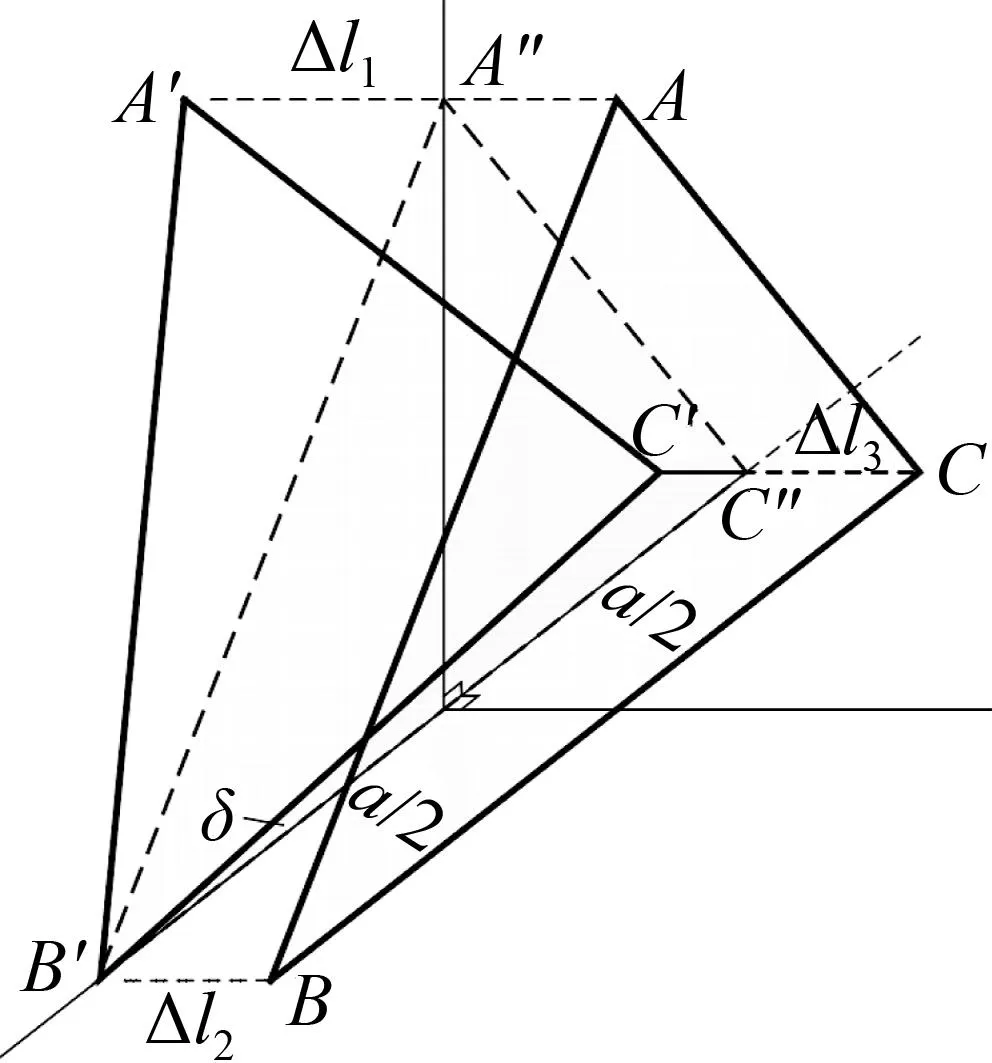
图9车轮前束角变化量的三点法测量原理
Fig.9Three points method measuring
principle of toe angle variation

图10前轮前束角与轮心垂直位移关系
Fig.10Front wheel toe angle vs wheel
center vertical displacement
将仿真结果图4与实车试验结果图10对比可以看出,优化曲线与实际测量曲线走势基本一致。前束角变化量实车试验、优化后、优化前前束角变化值分别为0.02°,0.017°,0.114°,实测前束角变化值与优化后相似度为85%。表明优化后前束角变化值明显优于优化前,且优化后相较于优化前前束角降低85.1%。
5讨论
从以上仿真试验可以看出:不足转向梯度试验和方向盘角阶跃试验表明峰值横摆角速度、稳态横摆角速度和调整时间动态响应特性随着前束角的变化而变化,前束变化值降低85.1%使得峰值横摆角速度、稳态横摆角速度和调整时间分别降低2.13%,2.07%,16.44%,不足转向梯度值最大降低0.1 deg/g。对于实车试验表明:实测前束角变化值与优化后相似度为85%,且经RBF神经网络优化后的点位相较于未优化的点位能够获得更优动态响应特性。本文使用RBF神经网络进行优化不需考虑前束角变化与断开点之间的具体关系,作为优化方法普适性更强,可以扩展到不同布置形式的转向梯形断开点优化设计中。在进行K&C实车试验对算法和模型进行验证在同类研究中也比较少见。
6结论
①建立RBF神经网络对转向梯形断开点在轮胎反向跳动工况下进行优化。
②使用优化后的断开点在Adams模型中与CarSim模型进行不足转向梯度试验和方向盘角阶跃试验,得出优化后的模型横摆角速度峰值、稳态横摆角速度和调整时间相较于未优化的模型分别降低2.13%,2.07%,16.44%。
③对实车进行K&C试验,得到前束角变化量实车试验、优化后、优化前前束角变化值分别为0.02°,0.017°,0.114°。优化后前束角变化值明显优于优化前,且优化后相较于优化前降低85.1%。
④实车试验验证了RBF神经网络优化算法精度和建立的模型有一定可信度,满足设计目标需求。
参考文献:
[1]中国大学生方程式汽车大赛规则委员会.中国大学生方程式汽车大赛规则(2014版)[S]. 北京:中国汽车工程学会,2014.
[2]高晋,杨秀建.车轮定位角对操纵稳定性指标影响的定量研究[J]. 工程设计学报,2014,21(3):251-258.
[3]SIMIONESCU P A, BEALE D.Optimum synthesis of the four-bar function generator in its symmetric embodiment: the Ackermann steering linkage[J]. Mechanism and Machine Theory,2002,37:1487-1504.
[4]朱发旺,尉庆国.转向梯形机构的设计及优化[J]. 内燃机与配件,2015(3):6-10.
[5]赵聪.FSAE赛车转向系统设计及性能分析[D]. 合肥:合肥工业大学机械与汽车工程学院,2015.
[6]向铁明,任恒山,朱益铭.赛车转向梯形优化设计方法厦门理工学院28号FSAE赛车转向梯形设计[J]. 厦门理工学院学报,2009,17(4):48-50.
[7]李君,邓正俊,郑维炜,等.FSAE方程式赛车转向梯形优化[J]. 农业装备与车辆工程,2014,52(12):10-13.
[8]韦超毅,蒋国平,周从钜,等.基于ADAMS软件的转向梯形计算机辅助设计[J]. 广西大学学报:自然科学版,2003,28(3):246-248.
[9]向铁明,周水庭,沈理真.FSC赛车转向梯形机构断开点仿真与优化设计[J]. 宁夏大学学报:自然科学版,2013,34(3):238-241.
[10]张凯,陈盼.FSAE方程式赛车转向梯形的联合优化设计[J]. 汽车实用技术,2015(4):72-74.
[11]卢永陵,熊璐.基于模拟退火算法的小型方程式赛车转向系统的设计与优化[J]. 装备制造技术,2015(5):141-143.
[12]姚汉波,唐应时,王焕美,等.FSAE赛车转向系统的仿真与优化[J]. 计算机仿真,2011,28(4):349-352.
[13]唐应时,朱彪,朱位宇,等.基于响应面方法的转向梯形优化设计[J]. 中南大学学报:自然科学版,2012,43(7):2601-2606.
[14]柴杰,江青茵,曹志凯.RBF神经网络的函数逼近能力及其算法[J]. 模式识别与人工智能,2002,15(3):310-316.
[15]李志魁.基于CarSim的整车动力学建模与操纵稳定性仿真分析[D]. 长春:吉林大学汽车工程学院,2007.
[16]王行.方程式赛车操纵稳定性研究[D]. 广东:广东工业大学机电工程学院,2013.
[17]陈思忠,倪俊,吴志成.基于特定赛道的方程式赛车转向梯形优化与虚拟试验[J]. 机械传动,2012,36(9):67-70.
[18]SMITH C.Tune to win[M]. Fallbrook, California, United States:Aero Publishers,1978:60-63.
[19]MILLIKEN W F, MILLIKEN D L.Racing Car Vehicle Dynamics[M]. Warrendale, Pennsylvania, United States of America: Society of Automotive Engineers,1995:709-728.
[20](美)GILLESPIE T D.车辆动力学基础[M]. 赵六奇,金达锋,译.北京:清华大学出版社,2006:135-161,188-207.
[21]杨建森.悬架K&C特性对汽车操纵的敏感性分析[D]. 长春:吉林大学汽车工程学院,2008.
(责任编辑梁健)
Steering trapezium splitting points optimization of FSC racing car based on RBF neural network
WU Ping, TANG Lan, QIAO Xu-qiang
(School of Automotive and Transportation, Xihua University, Chengdu 610039, China)
Abstract:In order to increase FSC(Formula Student China) car cornering response and handling stability, a steering trapezium splitting points RBF (radius basis function) neural network (NN) optimization algorithm is established. Firstly, 64 groups of raw data of steering trapezium splitting points are generated by insight module in Adams/car virtual model. Raw data are used for training RBF NN. Splitting points are optimized by trained RBF NN. Understeer gradient simulation and steer wheel step response simulation are contrasted between Adams/car model with optimized splitting points and CarSim model. The simulation results showed that optimized peak yaw rate, steady yaw rate and setting time decreased respectively 2.13%, 2.07%, 16.44%, and the maximum of under-steer gradient was reduced to 0.1 deg/g. Furthermore, wheel travel condition was tested on a real car to measure toe angle. Under condition that wheel center travel distance is ±15 mm at vertical direction, toe angle in real car test, with optimized model and un-optimized model changed to 0.02°, 0.017° and 0.114° respectively, and the toe angle of optimized model decreased alteration is 85.1%. Results of simulation and test showed that RBF NN algorithm has high reliability, provides an excellent cornering response and handling stability, and is a optimization method for quantization splitting points.
Key words:FSC car; splitting points of ackerman steering; toe angle; RBF neural network;K&C test
中图分类号:U461.6
文献标识码:A
文章编号:1001-7445(2015)06-1381-08
doi:10.13624/j.cnki.issn.1001-7445.2015.1381
通讯作者:唐岚(1963—),女,四川成都人,西华大学教授;E-mail:cs5765@163.com 。
基金项目:教育部“春晖计划”项目(13203642);四川省科技支撑计划项目(2013GZ0147-2);西华大学研究生创新基金(ycjj2015037)资助;汽车工程四川省高校重点实验室项目(szjj2014-073)
收稿日期:2015-08-24;
修订日期:2015-10-09

