基于改进布谷鸟算法的微网储能系统控制策略研究

曾　鸣，段金辉，刘英新，李　蓓

(1.华北电力大学新能源电力系统国家重点实验室， 北京102206；2.华北电力大学经济与管理学院， 北京102206； 3.中国电力科学研究院， 北京102206)



基于改进布谷鸟算法的微网储能系统控制策略研究

曾鸣1,2，段金辉1,2，刘英新2，李蓓3

(1.华北电力大学新能源电力系统国家重点实验室， 北京102206；2.华北电力大学经济与管理学院， 北京102206； 3.中国电力科学研究院， 北京102206)

摘要：为优化微网运行，以保障电力供需平衡并促进可再生能源消纳，对含储能的并网型微网的电池储能系统控制策略进行研究。首先，构建基于滚动时域控制的微网储能系统控制策略混合整数线性规划(mixed integer linear programming，MILP)模型；其次，采用改进的布谷鸟(modified cuckoo search，MCS)算法对模型进行计算；最后，进行算例分析，研究最优控制策略下微网信号与电池信号的特征，并对算法的收敛性与其他算法进行比较，以验证模型和算法的有效性。研究结果表明，不同的微网运行目标会影响储能系统控制策略，进而影响微网的信号特征；MCS算法在收敛速度、计算时间和经济性上较传统的布谷鸟(cuckoo search，CS)算法和差分进化(differential evolution，DE)算法有显著提高。

关键词：微网；电池储能系统；MILP；MCS；控制策略

近年来，微网作为多能互补的智慧型能源综合利用局域网得到了快速发展。其中，并网型微网与外部大电网相连接，可以实现并网和孤网两种运行模式的灵活切换。当分布式电源发电量满足微网用电时，微网控制系统会把多余的电送入主网；当分布式电源发电量不足时则由主网供电，形成双向调节平衡，充分满足用户对电能质量、供电可靠性和安全性的要求。我国已建成鹿西岛并网型微网等众多并网型微网。微网包含多种可再生能源发电，而可再生能源的出力时段与用户用电时段并不吻合，因此难以满足供需平衡[1-2]。而储能能够有效消除昼夜间峰谷差，平滑负荷，促进可再生能源的消纳[3]。基于此，本文对含储能的并网型微网的电池储能系统运行策略进行研究。

目前，国内外学者已经对电池储能系统控制策略进行了相关研究[4-11]，但前人研究存在两方面的问题，一是研究多为静态建模；二是采取的计算方法较为传统，在收敛时间和计算结果上都有待完善。因此，本文在模型构建中运用了滚动时域动态控制策略，在计算时采用改进的布谷鸟(Modified Cuckoo Search，MCS)算法，并将其与传统的布谷鸟(Cuckoo Search，CS)算法与差分进化(Differential Evolution，DE)算法进行比较，以验证模型和方法的有效性。

1微网储能系统控制策略模型

在实际的运行当中，微网储能系统的优化控制策略必须考虑交易电量、交易价格以及运行成本等各因素，各因素随着运行状态的不同也在时刻变化，因此需要引入动态预测的优化方法和概念。本研究基于滚动时域控制原理构建微网储能系统控制策略的MILP优化模型。

1.1　滚动时域优化

滚动时域优化是一种动态预测的优化方法。在具有不确定性的动态环境下进行预测时，很难达到理想中的全局优化，这时就需要反复进行局部优化以使预测结果更加接近全局优化。为了达到上述目的，在动态预测中引入滚动优化的思想。作为一种可以跟踪系统变化的优化控制策略，滚动时域优化方法能够通过不断推动优化集在时间轴上滚动并运用优化算法来求解子问题，进而通过求解子问题达到局部优化并通过不断滚动实现最终的全局优化。通过滚动时域优化，对微网储能系统的运行时段进行划分，并以步长的形式对系统的运行策略进行滚动模拟和优化。

滚动窗口技术是滚动时域优化的核心[12]，如图1所示。其中，PREk为第k个预测窗口，DOk为完工窗口，WAITk为等待窗口，滚动窗口时间步长为ΔT，预测窗口时间步长为ΔTPRE。系统在ΔT时间内进行滚动的局部优化，假设系统在经过时间步长ΔT后达到局部优化，则将已完工任务从预测窗口移入完工窗口，然后选取若干等待窗口中的任务移入预测窗口，选取新的滚动窗口时段开始新一轮的滚动优化。

图1　滚动时域方法的窗口滚动示意图

1.2　模型构建

未来微网储能系统的控制模块是基于AEMS(Advanced Energy Management System)实现的，结合滚动时域控制原理，本文研究的微网储能系统控制模块如图2所示。假设对于每一个时间步长，算法预测生成一个预估净需求功率向量DnetPRE以及不确定误差△DnetPRE。其中，DnetPRE表示预测的功率需求与可再生能源发电出力之间差额(kW)，此处以向量的形式表示。DnetPRE=Dnet表示算法预测的净需求功率向量等同于实际功率需求向量，即净需求被完美预测的情况，其中，净需求功率向量Dnet表示需求功率与风电场发电功率之间的实际差额(kW)。为了模拟储能设备最优的充放电策略，在每一个时间步长内都将形成一个MILP问题。因此，本文尝试采用滚动时域优化的方法对该问题进行求解。图2描述了含储能的微网系统的滚动时域优化方法。其中，C为成本(元)；Dbase为时域内需求功率基线(kW)；BEfinal为时域终点预测电池能量(kWh)；BE0为时域起点实际电池能量(kWh)；BPc为电池储能系统充电功率(kW)；BPd为电池储能系统放电功率(kW)。

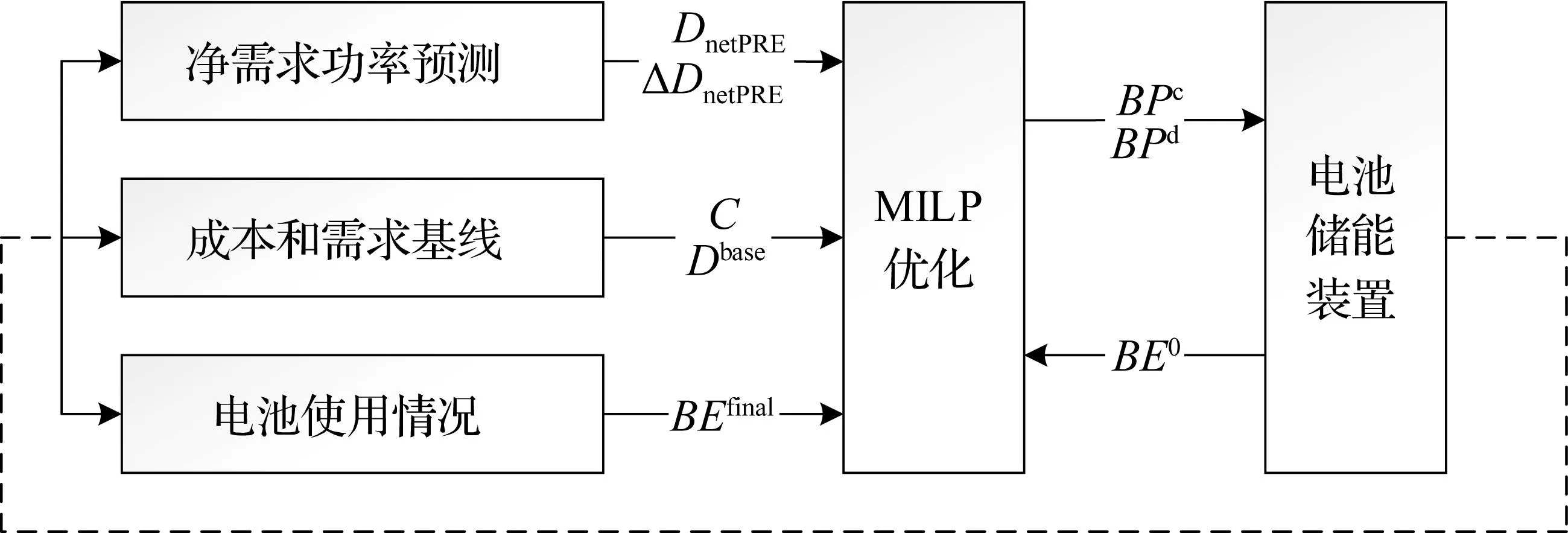
图2　滚动时域控制模块图解

1.2.1目标函数

设定模型的最优目标为微网储能系统运行成本的最小化，则本文所建立的基于滚动时域优化的微网储能系统充/放电控制策略模型的目标函数为：

(1)

式(1)中，优化变量的时间长度为T，即总的预测的时间区域，N为整个模型优化过程中所有的滚动时域窗口的数量，ΔT为滚动时域窗口的步长，即预测的步长，整个优化过程的总时长为NΔT。在每一步长范围内达到区域最优时即进行下一时域步长的优化。可以看到，式(1)中共有3个因式，其含义如下。

因式1表示系统的净用电成本。电力交易不同于系统充放电的行为，在储能系统进行充放电时，其所处的微网仍可以进行购入或售出的电力交易(微网同其他电网进行的电力交易)。其中，BPcb表示在电池储能充电时购自于电网部分的功率(kW)；VbT为微网从电网中购电的价格(元/kW)；BPcs表示在电池储能充电时售予电网部分的功率(kW，该情形下，储能设备无法将所有多余出力储存，系统边充电边向电网售电)；VsT为储能系统向电网售电的价格(元/kW)；BPdb为电池放电时储能系统购自于电网的功率(kW，该情形下，储能系统放电功率无法满足负荷需求与出力之间的差额，系统必须从其他电网购电)；BPds表示在电池放电时储能系统售予电网部分的功率(kW)。需要注意的是，当Dnet>0时，BPcs=0，也即需求过量时充电功率不再包含向电网售电的部分；当Dnet<0时，BPdb=0，也即当需求不足时放电功率不再包含从电网购电的部分。对于整个储能系统而言，其实时功率即为BP=BPcs+BPcb-BPdb-BPds，BP为正则表示总充电功率大于放电功率，系统电量不断增加，反之则放电功率大于充电功率，系统电量不断减少。

因式2表示电池的使用成本和信号平滑成本。BPc=BPcs+BPcb；BC为电池运行的成本(元/kWh)。BR为连续时域步长内电池储能系统功率比的改变量级(用来衡量电池平滑程度)(%)；CBR为平滑电池功率分布信号的成本(元)。

因式3给出了微网信号形成成本。GR为连续时域步长内微网功率的改变量级，CGR为平滑微网信号的成本(元)；D=BP+Dnet为整个系统的功率水平，也即系统的总电力需求功率(kW)。Dhigh为超过基准需求功率的最大功率值(kW)，Chigh为削减这一功率的成本(元)。Dmax为微网最大需求功率(kW)，Dmin为微网最小需求功率(kW)，Cflat为整平微网需求功率的成本(元)。

1.2.2约束条件

本节建立微网与电池储能装置运行控制的约束条件。文中所建立的模型主要考虑微网储能系统的电池储能装置充/放电状态决策约束、电池储能系统的能量与功率变化约束以及微网系统的信号约束3个部分。

①电池储能装置充/放电状态决策约束

电池充放电功率的变化范围约束如下：

0≤BPc≤BPc,max·α≤BPc,max，

(2)

0≤BPd≤BPd,max·(1-α)≤BPd,max，

(3)

式中，α∈[0,1]为二进制变量，对于第i个元件，αi=1表示充电，αi=0表示放电。BPc,max、BPd,max分别为储能系统额定的充/放电功率的最大值(kW)；BPc,max、BPd,max为当前电池剩余可充/放容量的限制。

微网从电网买/卖电的状态决策约束如下：

BPdb,max·(1-θb)≤BPdb≤BPdb,max，

(4)

BPds,max·(1-θs)≤BPds≤BPds,max，

(5)

BPcs,max·(1-θs)≤BPcs≤BPcs,max，

(6)

BPcb,max·(1-θb)≤BPcb≤BPcb,max·θb，0≤θs，θb≤1，

(7)

BPkdb,max=min(max(0,Pdk),BPd,max)，

(8)

BPkcs,max=min(max(0,-Pdk),BPc,max)，

(9)

对于k∈[1,NΔT]，k表示系统优化的特定时间区域，变量θb和θs表征微网储能系统的买/卖决策，为二进制变量，当其值为1时表示买卖决策发生，形成交易；当其值为0时则表示未进行买卖。式(8)、(9)表示所优化的时间区域内微网储能系统的BPdb和BPcs的最大值取决于负荷对储能系统的净功率需求Pdk。

②电池储能系统的能量与功率变化约束

电池能量水平约束如下：

(10)

式中，BE0为时域初始时的电池储能系统能量水平，BEmin和BEmax分别为最低和最高界限，εc和εd是充电/放电效率。

时域内最终电池能量水平约束如下：

εc·ΔTT·BPc-εd-1·ΔTT·BPd-BPloss·ΔTT1=BEfinal-BE0，

(11)

式中，BEfinal是期望的时域结束时电池能量水平，其值水平应确保电池储能量不被耗尽。

电池信号平滑和功率变化约束如下：

-ΔBPΔT≤BPkc+BPkd-BPk-1c-BPk-1d≤BRk≤ΔBPΔT，

(12)

由于k∈[1,NΔT]和BR≥0，因式ΔBP表示电池储能系统功率转换率的最大值(kW/h)。平滑电池功率曲线的目的在于减少微网内(电压)瞬变对储能系统的影响，否则将影响电池寿命。

③微网系统信号约束

A-EMS控制器可以调节微网与电网公共联合点处的功率分布曲线。为了调节与削弱超过需求基线的峰值功率，使用下述不等式约束：

|Dnet|≤|Dhigh-Dbase|，

(13)

式中，Dbase为系统内的基准需求功率，Dbase，Dhigh≥0，即系统净需求功率的绝对值在超过基准需求功率的最大功率值与系统基准需求功率之间的差值的绝对值范围内。

微网信号整平约束如下：

Dmin≤(BPcs+BPcb)-(BPdb+BPds)+Dnet≤Dmax，

(14)

式中，Dmin，Dmax分别为微网系统运行功率水平的最小值和最大值，该约束表示微网系统内储能电池的充放电功率以及系统的净功率需求之和必须在系统所能承载的最小功率和最大功率之间。

微网功率信号平滑约束如下：

-GRk≤(BPkcs+BPkcb)-(BPkdb+BPkds)+(Dnet,k-Dnet,k-1)-(BPk-1cs+BPk-1cb)+(BPk-1db+BPk-1ds)≤GRk，

(15)

式中，k∈[1,NΔT]，GR≥0，该约束表示在连续的两个时域内微网系统的运行功率的大小必须在该时域范围内微网功率的改变量级约束以内。

2MCS算法

通过滚动时域优化方式构建的微网储能系统控制策略模型能够实现对系统运行状态的滚动模拟和预测，为了对模型进行求解以得出系统最优运行策略，本模型引入MCS算法。CS算法由Yang等[13]于2009年提出，该算法通过模拟某些种属布谷鸟的寄生育雏来有效地求解优化问题。CS算法基于Lévy飞行进行搜索，具有高度的方向与距离随机性，可以轻易地跳出当前搜索区域并跳入另一区域进行搜索，其全局寻优能力十分强大，但也存在一些问题。因此，本节提出MCS算法来解决微网储能系统控制策略问题。

2.1　CS算法概述

CS算法启发于自然界中布谷鸟的寄巢产卵的行为。与一般鸟类不同，布谷鸟繁衍下一代的方式为寄生产卵，它们将产下的蛋放入其他鸟类的巢中，让其他鸟类为其孵化。当这些鸟类发现巢中有外来的蛋时会采取两种措施，一是丢弃外来的蛋，二是放弃自己的巢，然后另选地点搭建新巢。CS算法的主要思想就是通过Lévy飞行路径产生候选鸟巢以及采用精英保留策略更新当前鸟巢位置，以使鸟巢位置实现或接近全局最优。CS算法在处理单目标优化问题时具备高度的寻优性能。这一算法包含3个理想假设：①一只布谷鸟一次只产一个蛋，且随机选择放置该蛋的巢;②在一组随机选择的巢中，适应性最好的鸟蛋将在巢中被保留到下一代;③可用的鸟巢数量n是固定的，外来鸟蛋被巢主人发现的概率P∈[0,1]。

基于上述3个假设，CS算法中布谷鸟寻找最优鸟巢的步骤及更新公式如下。

首先，通过Lévy飞行更新。在智能算法中，采用Lévy飞行搜索机制能扩大搜索范围，增加种群多样性，更容易跳出局部最优解[14]。建立更新公式如下：

xig+1=xig+α⊕L(λ)，

(16)

L(λ)~u=g-λ,1<λ≤3，

(17)

式中，xig+1为第g+1代中的个体i；α为控制随机搜索范围的步长控制向量；⊕为点对点乘法；L(λ)为Lévy随机搜索步长，服从Lévy分布。

其次，通过固定发现概率P进行更新。每次迭代产生新巢后，比较布谷鸟蛋被寄主发现的概率P与随机数φ∈[0,1]，若P<φ，则对xig+1进行随机改变以生成新个体，反之则不进行改变。新个体生成方式如下：

xig+1=xig+φ·(xjg-xkg),i=1,2,…,n，

(18)

式中，xjg与xkg为第g代的两个随机解，鸟巢更新后的位置仍记为xig+1。在CS算法中，P与α为两个重要参数，通常设为固定值，在迭代过程中保持不变。在迭代寻优过程中，若P较大，α较小，则算法收敛速度将会提升但全局最优解的精度将会下降；若α较大，P较小，则将导致迭代次数大幅增加。

可见，一方面,CS算法生成初始解的方式随机性较大，因此,为获得高质量初始种群就需提高种群规模。另一方面，CS算法依赖于Lévy飞行更新种群中宿主鸟巢的位置，群体间信息沟通不足，个体间无法分享各自的知识与经验，充分发挥群体协作优势，因此需要对算法进行改进以提高其性能。

2.2　改进的CS算法

基于上述问题，本文对CS算法进行两个方面的改进：一是参照遗传算法引入变异机制，以增加进化过程中种群的多样性；二是参照DE算法嵌入变异、交叉、选择操作，以提升群体间的竞争与合作程度，从而增加优化结果的精度。

2.2.1增加种群多样性

CS算法中初始个体生成方式如下：

xi=xmin+ω·(xmzx-xmin),i∈[1,SIZE]，

(19)

式中，xi为第i个初始种群个体；xmax和xmin分别为所生成的种群个体的上、下限；ω为分布在[0,1]之间的均匀随机数；SIZE为种群规模。随着种群规模的不断扩大，优化计算的范围也不断扩大，会对算法寻优造成不利影响。因此，本文对算法产生的每一代最佳个体都进行变异，以提升种群个体的质量。变异机制如下：当CS算法迭代至第g代时，选择当前的最佳鸟巢xbestg，避免其直接遗传到下一代，而是继续进行变异操作，且随着进化代数的增加变异步长逐渐减小。变异机制如下：

xbest′g=xbestg+{α1·cos[π·(Giter-1)/2(GMAX-1)}⊕τ，

(20)

式中，xbest′g为变异后鸟巢的位置；τ∈[0,1]为1×D向量，服从标准正态分布；D为优化问题的维数。GMAX为算法的最大进化代数；Giter为当前的进化代数。

为确保变异朝着有利的方向进行，将xbest′g与xbestg的适应度值进行比较，保留适应度值较优的个体xBESTg并遗传到下一代，以实现有效的变异操作：

(21)

式中，FIT为个体的适应度值。在本文中，微网储能系统控制运行优化属于极小值优化问题，而CS算法的优化同样朝最小值的方向进行。因此，此处直接将目标函数(1)的值作为CS算法的适应度值FIT。

2.2.2差分进化算子

作为一种基于种群差异的进化算法，DE算法通过变异、交叉、选择操作提升群体间的竞争与合作程度，以形成有效的信息共享机制，是一种有效的全局优化算法。参考差分算法的信息共享机制，本文按照如下方式构造差分算子嵌入多目标CS算法中。

①变异操作。将所有鸟巢视为一个种群，xig为需要变异的个体，在当前种群中随机选择两个个体xrand1g，xrand2g，并通过如下差分策略产生变异个体yig：

yig=xig+M·(xrand1g-xrand2g)，

(22)

式中，M为缩放因子。变异后的个体遗传了父体xig的部分信息，同时借鉴了个体xrand1g，xrand2g的信息，实现了个体间的信息传递。

②交叉操作。交叉操作是通过重组父体xig与变异个体yig以产生候选个体zig。个体zig第σ维分量取值按如下规则：

(23)

式中，r为[0, 1]的均匀随机数；CR为交叉概率；d为随机选定的某一维度，用来确保至少有一维分量值由变异个体贡献。

③选择操作。将候选个体zig与父体xig的支配关系进行比较，并将优势个体遗传到下一代，即选择操作。这一操作用于实现精英个体的保留。选择操作规则如下：

(24)

式中，random(zig，xig)表示等概率随机选择zig和xig某一个体。

MCS算法流程图如图3所示。

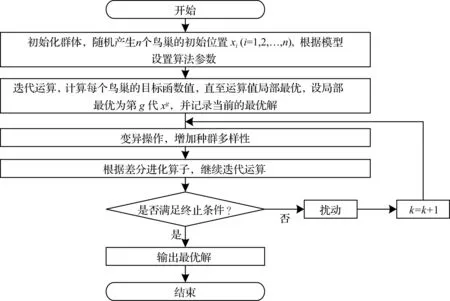
图3　MCS算法流程图

3仿真结果

本节选取某微网储能系统进行算例分析,研究系统在最优控制策略下各种目标下的微网信号与电池信号特征，并对算法的收敛性与其他算法进行比较，以验证模型和算法的有效性。

算例在一个包含商用与居民的环境中进行，系统的发电来自风力机组发电,典型日系统负荷需求情况如图4所示,典型日系统风力发电情况如图5所示,微网系统采用分时电价如图6所示。

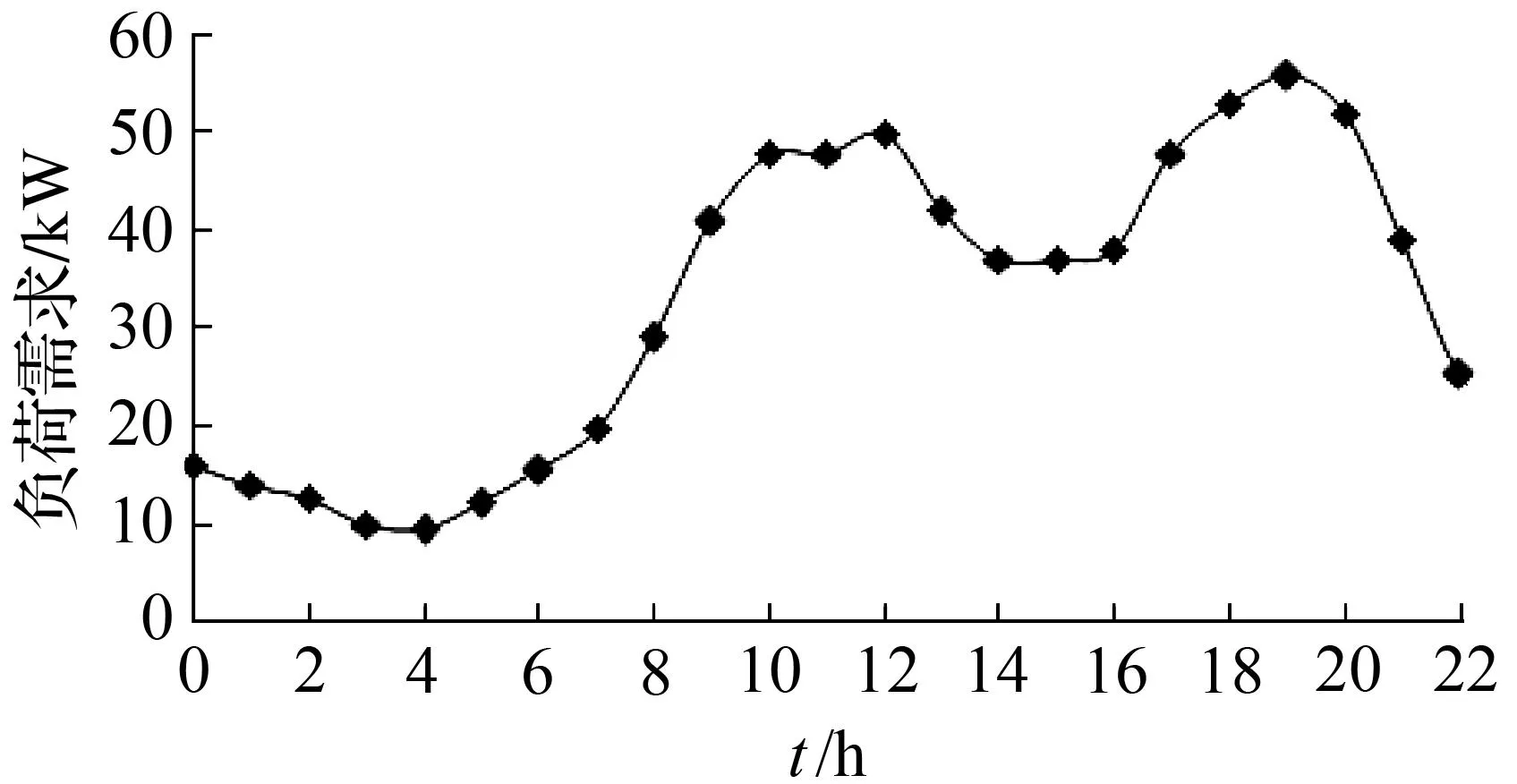
图4微网系统负荷需求情况

Fig.4Load demand of the micro grid

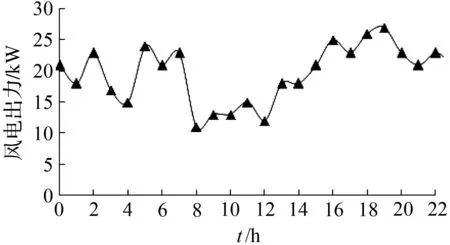
图5微网系统风电出力情况

Fig.5Wind power output of the micro grid

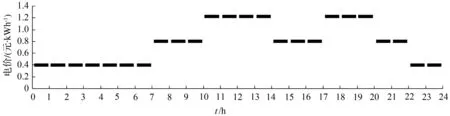
图6　微网分时电价

变量BEmin/kWhBEmax/kWhεcεdBPc,max/kWBPd,max/kWBPloss/kWVb=Vs数值015113300

基于上述数据，研究不同目标下微网和电池储能系统功率信号特征，此处设定3个目标：①微网系统削峰目标，即在可削减的前提下通过储能系统削减微网需求的峰值，使其维持在10 kW及以下水平，此时削峰成本Chigh=1，其他成本为0；②微网系统信号整平目标，即在对微网削峰的基础上利用储能系统提升微网需求的下限，使其维持在2 kW及以上水平，并根据预测的系统净需求的上限和下限进行调整，此时微网信号整平成本Cflat=1，其他为0；③微网系统信号平滑目标，即在微网系统信号整平目标的基础上对微网信号进行平滑处理，此时，微网信号平滑成本CGR=ΔT，其他成本为0。时域范围为24 h，时域区间大小可随机设定，此处为计算方便将其设置为ΔT=[0.50.50.50.50.50.51.01.01.02.02.02.03.03.03.03.0]T。

为对所建立的微网储能系统的最优控制模型进行验证，本文采用MCS算法进行求解，并与CS算法及DE算法的优化结果作对比。运用MCS算法对微网储能系统的优化控制策略进行求解时，设置种群规模SIZE=50，最大迭代次数GMAX=200，发现概率P=0.25，交叉概率CR=0.85，缩放因子M=0.4，得到不同目标下的微网信号特征如图7~图10所示。其中，细虚线表示整个运行时间区域内微网系统运行功率的上限和下限约束，粗实线表示系统的实际运行功率。图7体现了初始微网净需求功率分布情况；图8体现了峰值削减目标下的微网信号特征；图9体现了微网信号整平目标下的微网信号特征，对系统净需求分布的整平效应；图10体现了微网信号平滑目标下的微网信号特征，实现了功率波动的最小化。

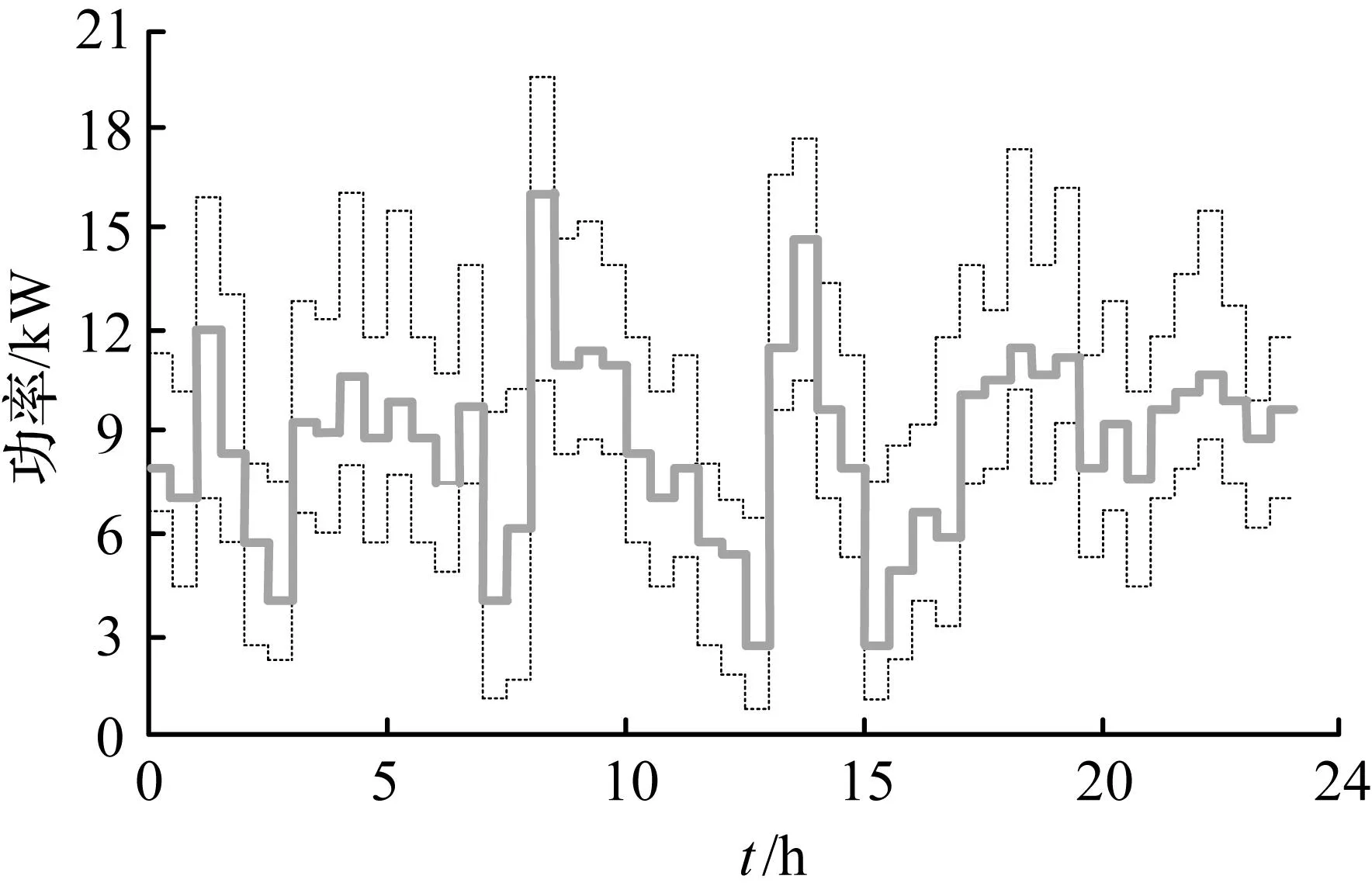
图7初始微网净需求功率分布情况

Fig.7Power distribution of the

initial net demand of micro grid

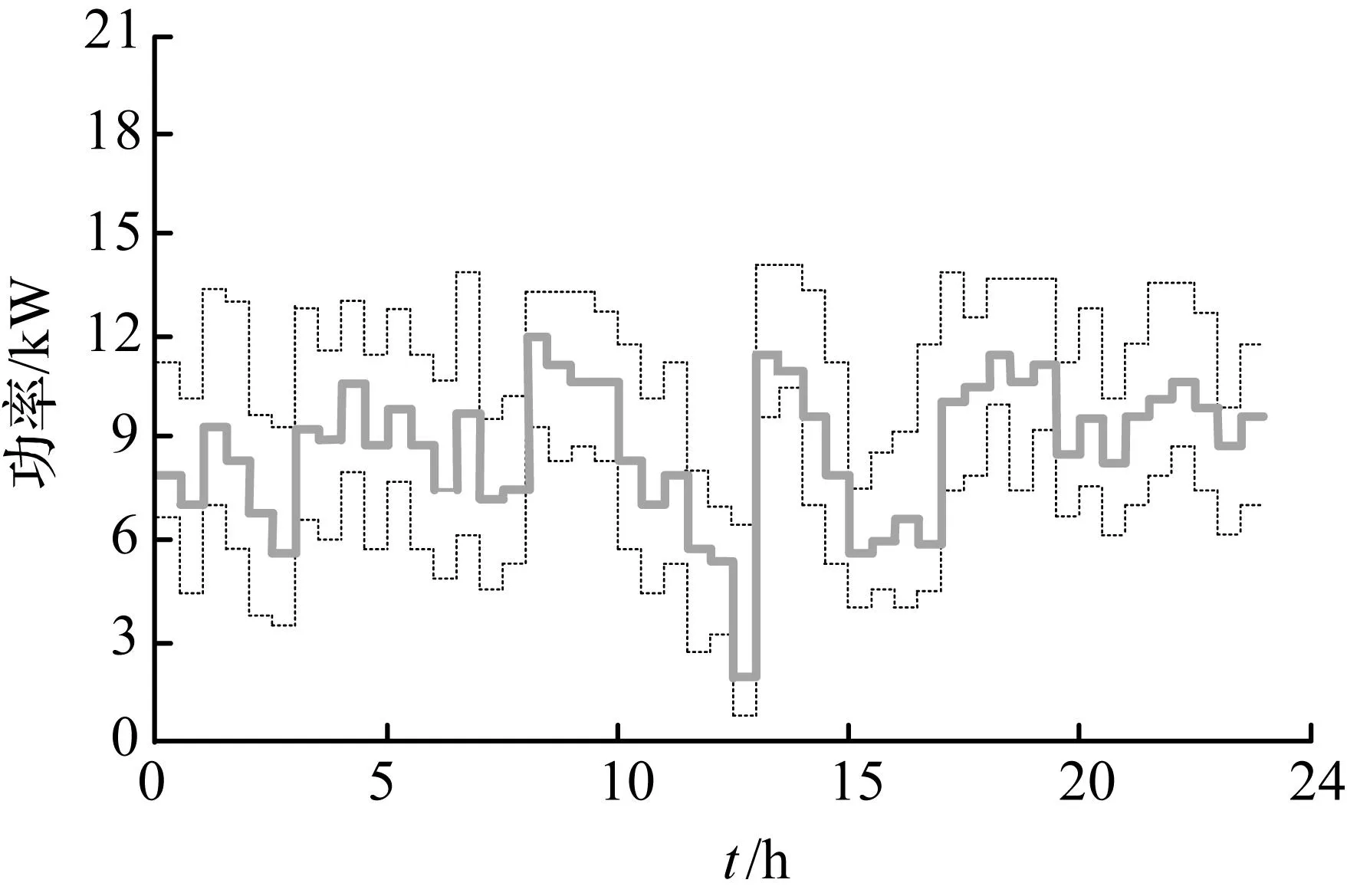
图8峰值削减目标下的微网信号特征

Fig.8Signal characteristic of the micro

grid under the object ofpeak-shaving

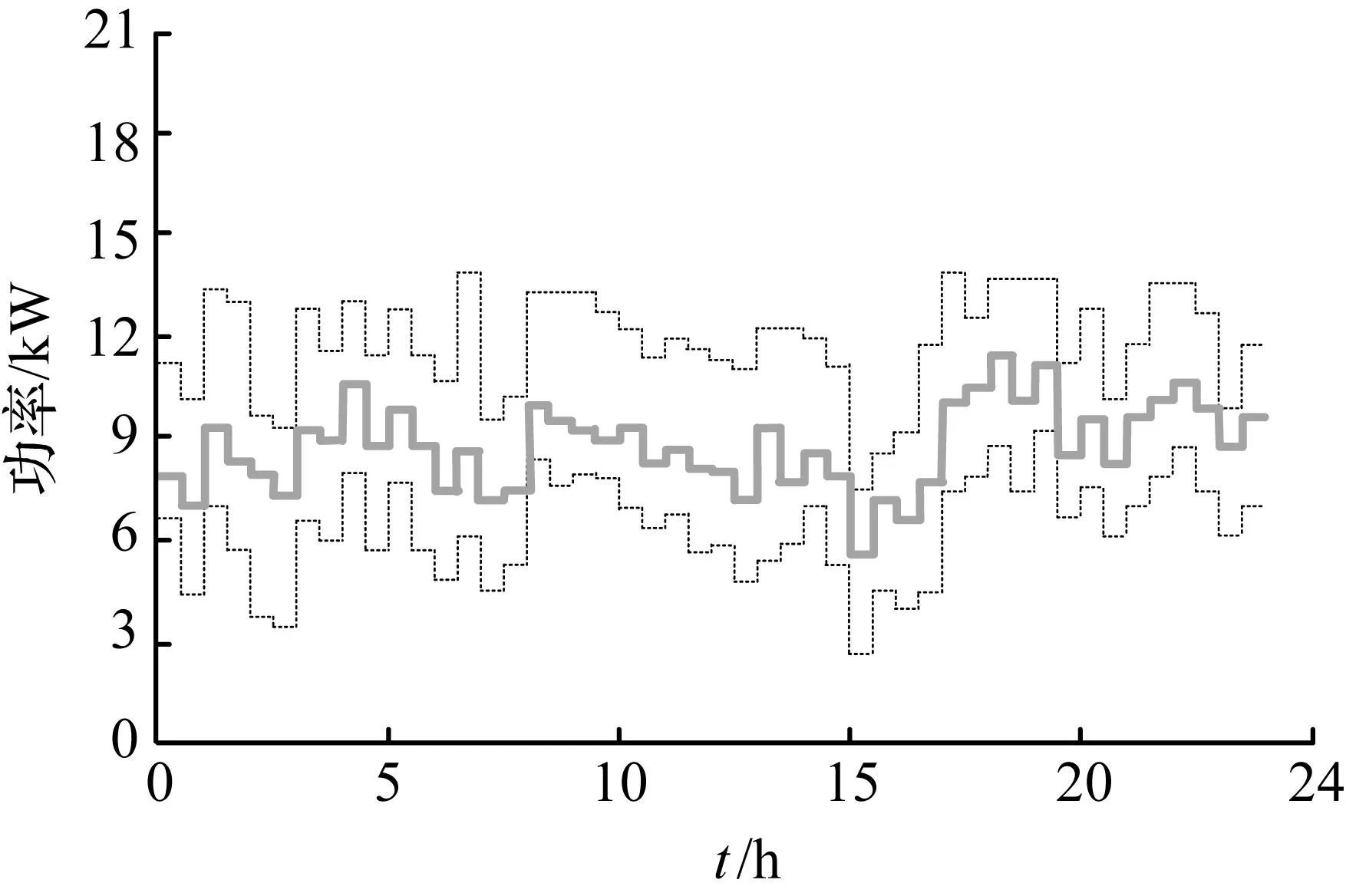
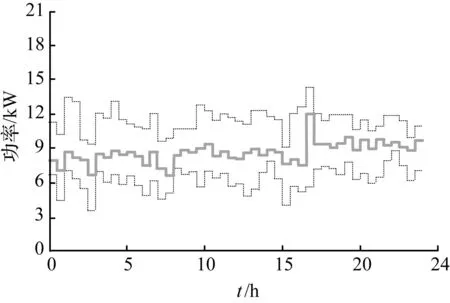
图10微网信号平滑目标下的微网信号特征

Fig.10Signal characteristic of the micro

grid under the object of smoothing

在对微网系统信号整平、平滑处理的基础上，同时运用CS算法与DE算法，以研究MCS算法在收敛性和计算时间方面的改进。计算的微网系统运行成本结果如图11所示。

可以看到，与CS算法、DE算法相比，MCS算法收敛速度更快，并且在维持系统正常运行水平的情况下达到运行目标的成本最低，有效实现了效率提升和成本节省，从而验证了本文所建立的基于MCS算法的微网储能系统控制策略优化模型的科学性及有效性。

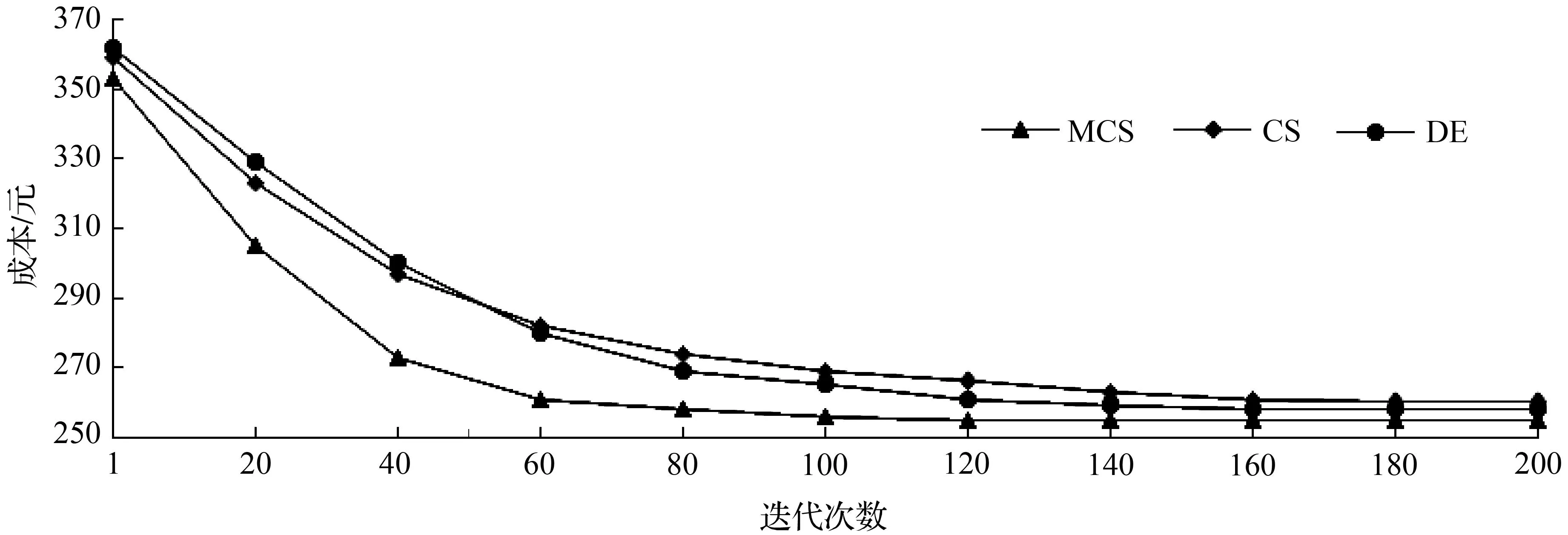
图11　MCS算法与CS算法、DE算法的迭代过程对比

4结论

本文构建了基于滚动时域预测的并网型微网储能系统动态控制策略模型，并提出了MCS算法对算例进行计算。结果表明，不同的微网运行目标会影响储能系统控制策略，进而影响微网的信号特征。同时，MCS算法在收敛速度、计算时间和经济性上较传统的CS算法和DE算法有显著提高。但本文未对可再生能源出力进行建模，也未包含对电动汽车充放电等的研究，未来可以进一步完善。

参考文献：

[1]ZENG Ming，DUAN Jin-hui，WANG Liang，et al.Orderly grid connection of renewable energy generation in china: management mode, existing problems and solutions[J]. Renewable and Sustainable Energy Reviews，2015，41(1)：14-28.

[2]LU Yong-xiang.Review and prospect of clean, renewable energy utilization[J]. Science & Technology Review，2014，32：15-26.

[3]王松岑，来小康，程时杰，等.大规模储能技术在电力系统中的应用前景分析[J]. 电力系统自动化，2013：37(1)：3-9.

[4]张步涵，陈奕，代晓康，等.微网中分布式储能系统的控制参数优化方法[J]. 华中科技大学学报：自然科学版，2014，42(12)：1-5.

[5]苗风东，陈永超，许忠敏.光伏微网系统中储能单元的控制研究[J]. 电源技术，2014，38(7)：1295-1297.

[6]毕锐，吴建锋，丁明，等.孤立微网多元储能与柴油发电机协调控制策略[J]. 电力系统自动化，2014，38(17)：73-79，97.

[7]KUMARS R，KUMARS M，CANDELA J，et al.Intelligent voltage control in a DC micro-grid containing PV generation and energy storage[C]//Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference. Chicago, IL, USA: IEEE, 2014:1-5.

[8]VASILJEVSKA J，PECAS LOPES J A，MATOS M A.Integrated micro-generation, load and energy storage control functionality under the multi micro-grid concept[J]. Electric Power Systems Research，2013，95：292-301.

[9]NAVID E,EBRAHIM F.Distributed charge/discharge control of energy storages in a renewable-energy-based DC micro-grid[J]. IET Renewable Power Generation，2014，8(1)：45-57.

[10]唐文强，吕智林，胡立坤，等.直流微电网孤立运行控制策略研究[J]. 广西大学学报：自然科学版，2014，39(5)：1027-1033.

[11]马晓娟，吕智林，卢子广，等.独立运行的风/光/蓄微电网系统能量动态优化研究[J].广西大学学报：自然科学版，2013，38(2)：431-438.

[12]刘国宝，张洁.基于改进滚动时域优化策略的动态调度方法[J]. 机械工程学报，2013，49(14)：182-190.

[13]YANG X，SUASH D.Cuckoo search via Lévy Flights[C]//Proceedings of World Congress on Nature &Bio-logically Inspired Computing.Piscataway，IEEE Publications，2009：210-214.

[14]RANI K N A，WEE F H，MALEK M F A.Modified cuckoo search algorithm in weighted sum optimization for linear antenna array synthesis[C]//2012 IEEE Symposium on Wireless Technology and Applications (ISWTA). Bandung，Indonesia: IEEE, 2012：210-215.

(责任编辑裴润梅)

Study on the control strategy of micro grid energy storage system based on modified cuckoo search algorithm

ZENG Ming1,2, DUAN Jin-hui1,2, LIU Ying-xin2，LI Bei3

(1. State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources,

North China Electric Power University, Beijing 102206, China;

2. School of Economics and Management, North China Electric Power University, Beijing 102206, China；

3.China Electric Power Research Institute, Beijing 102206, China)

Abstract:To optimize the running of micro grid to guarantee the supply and demand balance of electricity, and to promote the utilization of renewable energy. The control strategy of micro grid energy storage system is studied. Firstly, the mixed integer linear programming model is established based on the receding horizon control. Secondly, the modified cuckoo search algorithm is proposed to calculate the model. Finally, a case study is carried out to study the signal characteristic of micro grid and batteries under the optimal control strategy, and the convergence of the modified cuckoo search algorithm is compared with others to verify the validity of the proposed model and method. The results show that, different micro grid running targets can affect the control strategy of energy storage system, which further affect the signal characteristics of the micro grid. Meanwhile, the convergent speed, computing time and the economy of the modified cuckoo search algorithm are improved compared with the traditional cuckoo search algorithm and differential evolution algorithm.

Key words:micro grid; battery energy storage system; mixed integer linear programming; modified cuckoo search algorithm; control strategy

中图分类号：TM727; TK02

文献标识码：A

文章编号：1001-7445(2015)06-1414-10

doi:10.13624/j.cnki.issn.1001-7445.2015.1414

通讯作者：曾鸣(1957—)，男，山西太原人，华北电力大学教授，博士生导师；E-mail： zengmingbj@vip.sina.com。

基金项目：国家自然科学基金资助项目(71271082)；中央高校基本科研业务费专项资金(2014XS53)

收稿日期：2015-09-21；

修订日期：2015-09-25