基于小生境粒子群算法的SPWM逆变器准PR控制优化研究
基于小生境粒子群算法的SPWM逆变器准PR控制优化研究
王永林1, 艾明2, 瞿博阳1
(1.中原工学院, 郑州 450007; 2.郑州升达经贸管理学院, 郑州 451191)
摘要:研究了一种采用小生境粒子群算法优化设计SPWM逆变器准比例谐振(PR)控制器参数的方法。逆变器采用输出电压瞬时值反馈和电感电流反馈双闭环控制。PR控制可以克服常规PI控制难以消除交流输入系统稳态误差的缺陷,但在控制器参数设计上没有成熟技术。为此,给出采用LCL滤波器双环控制SPWM逆变器的数学模型和结构框图;用小生境粒子群算法构造灾变算子、迁徙算子和隔离算子,增强种群的多样性和算法的优化性能。介绍了采用小生境粒子群算法优化准PR控制器的步骤。对开环控制、PI控制和准PR控制的控制效果进行比较,验证了小生境粒子群算法的性能。
关键词:SPWM;逆变器;小生境技术;粒子群算法;准比例谐振(PR)控制;LCL滤波器
中图分类号:TM464;TP181
文献标志码:A
DOI:10.3969/j.issn.1671-6906.2015.03.003
Abstract:A parameter design method of the quasi proportional-resonant (PR) controller of a single-phase voltage SPWM inverter using an improved niching particle swarm optimization (PSO) algorithm is studied in this paper. The inverter adapts the double closed-loop control strategy with the instantaneous output voltage and inductor-current feedback. PR control strategy can overcome the disadvantages of the traditional PI control strategy which can not eliminate the steady-state error of AC input. However, there are some questions in designing for PR controller. The mathematical model and system structure of the SPWM inverter with LCL output filter are given. A niching PSO algorithm is presented which uses cataclysm operator, emigration operator and isolation operator to maintain the diversity of the population and improve the global optimizing ability. The steps of optimizing the parameters of PR controller using niching PSO algorithm are demonstrated. In comparison with open-loop control method and PI control method, the test results verify the performance of the proposed method.
收稿日期:2014-10-22
作者简介:张五一(1955—),男,河南洛阳人,教授,主要研究方向为智能检测技术。
文章编号:1671-6906(2015)03-0019-05
逆变电路可实现直流电能到交流电能的变换,是UPS、微电网、智能电网的关键装置[1],被广泛应用于电力系统、交流传动、工业电源、家用电器和航空航天等领域[2]。为了提高逆变器输出性能,人们引入了PI控制、滞环控制、无差拍控制、重复控制、比例谐振(PR)控制等控制策略[3]。PI控制不能消除交流输入信号的稳态误差;滞环控制不能实现无静差控制且开关频率不固定[3-4];无差拍控制依赖精确数学模型,鲁棒性不强,重复控制动态性能较差;PR控制能够实现交流信号的无静差控制,且动态性能较好,但在抑制高次谐波和控制器参数设计方面存在不足。
本文研究一种双环控制的单相电压型SPWM逆变器。逆变器外环采用瞬时电压反馈,控制器采用准PR控制,并采用小生境粒子群算法优化设计控制器参数;内环采用电感电流反馈,控制器采用比例控制;采用非对称T型输出滤波器来抑制高频谐波并减少环流。PWM控制波采用单极倍频[5]方式产生。本文将准PR控制与外环采用工程设计法设计的PI-P双环系统和开环控制做了比较分析。
1电压电流双环控制系统
双环控制电压型逆变器原理如图1所示。开关管T1、T2、T3、T4构成了H型桥式电路,电感L1、L2和电容C构成了非对称T型(LCL)输出滤波器,Z为负载,Ud为直流侧电压。电压控制器的输出作为电流控制器的输入,电流控制器的输出作为调制波,采用单极倍频方式生成SPWM驱动信号来控制开关管导通和关断。uc和io为前馈补偿控制,用于抵消结构负反馈的影响。

图1 电压电流双环控制逆变器原理框图
1.1单相逆变器数学模型
桥式电路的输出ui(LCL滤波器的输入)和LCL滤波器的输出uo之间的关系可通过机理建模法得到(见图1)。其电路方程(以阻感性负载为例,纯阻性负载,令L=0即可)如式(1):
(1)
式中:i1为电感L1上的电流(LCL滤波器输入电流);
uc为滤波电容电压;uo为滤波器输出电压。
式(1)经过拉普拉斯变换可得双环系统的动态结构(见图2)。
图2中:AVR是电压控制器;ACR为电流控制器;SPWM为逆变桥;Ki为电流反馈系数;Ku为瞬时电压反馈系数;Kc为电容电压正反馈系数,取逆变桥增益的倒数,以抵消电容电压结构负反馈;Ko为负载电流正反馈系数,通过合理设计,抵消负载电流结构的负反馈,以便抑制负载变化对系统的影响。逆变桥输出和输入之间的传递函数为比例纯滞后环节,为了方便,传统设计中一般按纯比例环节处理,本文设计PR控制器时按惯性环节处理(数学模型不再单独列出)。

图2 双环控制逆变器动态结构图
电流环以滤波电感L1的电流作反馈,不仅能达到以滤波电容电流为内环的控制效果,还可以对逆变器的输出进行限流保护,以防止电流突变造成设备损坏[3]。
1.2控制器数学模型
电流环采用比例控制器,其数学模型为:
GACR(s)=Gi
(2)
式中,Gi为该比例控制器的比例系数。
电压环采用准比例谐振控制器,其表达式为:
(3)
式中:Kv为比例增益,影响系统稳态性能和抗干扰能力;Kr为谐振增益,影响控制器的增益;ωc为截止频率,影响控制器的增益和带宽;ωo为基波角频率或谐振频率。谐振控制器消除的是对应频率信号的稳态误差。ωc的引入,能抑制谐振频率附近交流信号的扰动,也就是抑制电网频率波动的扰动[4-6]。
准PR控制器中Kv和Kr的值一般需要根据经验、系统的限制和要求折中考虑[4],有时候需要反复观察和试凑,给应用带来了不便。因此,本文采用小生境粒子群算法来优化确定Kv和Kr的值。
电压环若采用常规PI控制器,则其数学模型为:
(4)

2小生境粒子群算法
与其他进化算法相比,粒子群算法具有存储量少、计算简单、鲁棒性好等优点,但传统粒子群算法存在早熟收敛、无法调节搜索进程等问题。标准粒子群算法的速度和位置更新公式为[7]:
(5)
(6)

生物学中处于分离的孤立地理小生境中的物种在不进行竞争或交配等信息交流的情况下即能独立进化。将生物学中的小生境概念引入进化算法,可提高种群的多样性和算法的全局搜索能力,避免早熟收敛。目前的小生境技术主要有适应度共享策略[9]、排挤策略[10]、序列小生境[11](Sequential Niching)、聚类策略[12]、隔离策略[13]等等。这些小生境技术多采用欧氏距离进行种群划分,计算量较大,小生境半径之类的参数也没有通用的确定方法。本文提出的基于适应度划分的小生境粒子群算法对专家经验依赖不强,附加计算量也较小。
本文的小生境算法包括灾变算子、迁徙算子和隔离算子。当有大灾害诸如大地震、战争,可能导致小生境群体灭绝,群体中不再有更优秀的个体时,群体进化也多呈随机性,故本文对连续多代不进化的子群,采用随机初始化的策略,称为灾变算子。生物群体虽然按群落生存进化,但迁徙现象难以避免,某些灾难诸如饥荒也会导致部分个体出走;间隔一定代数将部分或全部粒子重新归类,称为迁徙算子。生物进化会产生某些大融合,如两个部落变为一个部落、两个鸟群飞到同一个食源,这样会导致进化单一化,所以当两个子群最优值接近时,将差的子群重新初始化,以避免实际的小生境减少,称为隔离算子。
本文提出的小生境粒子群算法可归纳如下:
Step1:初始化粒子种群,生成N个小生境子群。
Step2:计算适应度。
Step3:实施灾变算子,但保存最优个体且不参与后续进化。
Step4:实施迁徙算子,粒子按随机方式重新划分小生境,小生境数目和规模不变。
Step5:实施隔离算子。首先计算各子群之间最优适应度之差△fij以及最优与最差适应度之差△f。如果|△fij|<|△f|/N0,则适应度差的子群重新初始化,N0为大于N的整数。
Step6:每个小生境子群按式(5)和(6)独立进化。
Step7:如果满足结束条件,则停止迭代并输出优化解,否则转Step2。
3控制器参数设计
双环控制有两个控制器:电压控制器和电流控制器。本文的电流控制器采用比例控制,电压控制器采用准比例谐振控制。为了和常规PI控制器控制效果对比,便于验证与重现,本文给出了采用工程设计法设计电压环PI控制器的方法。
逆变器主电路参数为:母线电压350 V,输出电压220 V,L1=1.15 mH,L2=0.1 mH,C=90 μF,逆变器增益KSPWM=350/1。并且,额定负载电阻R=8 Ω,电容电压反馈系数Kc=1/350,电感电流反馈系数Ki=0.02,负载电流反馈系数Ko=0.02,瞬时电压反馈系数Ku=0.004,开关频率fk=10 kHz。
3.1电流环控制器参数设计
采用电容电压正反馈抵消其结构负反馈后,电流环开环传递函数为(此处忽略逆变器滞后):
(7)
确定电流环剪切角频率ωci后,根据式(8)可求得Gi。

(8)
对电源产品来说,剪切频率通常为开关频率的1/4或者1/5[14],甚至更小。这里取ωci=2π×100 00/4=500 0π,则:

3.2电压环控制器参数设计
3.2.1PR控制器参数设计
由于准PR控制器的Kv和Kr两个参数需要确定,故本文算法中每个粒子的位置包含两个优化参数,对应一个控制器。适应度函数可采用下述形式:
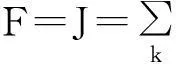
(9)
式中:e(k)为误差;J为控制指标;F为适应度函数(最小最优)。控制器参数优化设计一般采用计算机仿真技术,可以多次重复操作而不损坏设备,也能大大节省时间。这里采用MATLAB6.5作为仿真软件,通过SIMULINK建立系统仿真模型。模型采用传递函数形式,以减少仿真计算时间。参数设计出来后,再采用SimPowerSystems电力系统工具箱进行仿真系统检验。由于它是理论模型,与实际系统存在差异,因此优化的结果也不必苛求最优,求出满意解即可。
在具体优化时,将初始参数赋给SIMULINK仿真模型,通过采样取得系统输出序列,根据式(9)计算适应度来评价该组参数对应的性能,然后采用优化算法调整参数值,再传给SIMULINK仿真模型进行仿真评价。这样反复操作,进化寻优。
小生境粒子群算法优化准PR控制器的步骤如下:
(1) 初始化:初始化群体规模、参数初始值、小生境数目、惯性权重、最大迭代次数、各粒子的初始位置和初始速度等。
(2) 计算适应度:将粒子位置转化为两个控制器参数Kv和Kr,传递给SIMULINK仿真模型进行仿真,采用式(9)计算控制指标,得到每个粒子的适应度,进行适应度评价。
(3) 采用本文提出的小生境粒子群算法迭代更新参数。
(4) 检查是否满足停止条件,若满足,则搜索停止,输出结果;否则,返回(2)继续搜索。
采用优化算法设计控制器参数,不苛求对模型做进一步的简化,所以更能接近实际。在参数优化时,将逆变器视为惯性环节,时间常数取开关周期的一半,即TSPWM=1/(2fk)= 50 μs。取ωc=6 rad/s,步长为1 μs。
经优化,本文取Kv=4.5,Kr =1 508.8。
3.2.2PI控制器参数设计
这里采用工程设计法,基于闭环幅频特性峰值Mr最小准则,按典型II系统设计[15]。
采用负载电流正反馈抵消结构负反馈后,可以不考虑负载电流的影响,但采用工程设计法校正成典型系统,对被控对象的传递函数是有要求的,做必要的近似处理是难免的。由图2可知,uc到uo的传递函数为:
(10)
通过适当设计,使L2远小于负载阻抗,可忽略L2。由式(10)可知,此时uo≈uc。由式(7)可得到电流环的闭环传递函数,然后串上电容环节1/Cs(见图2),可得电压环被控对象:
(11)
文献[1]研究表明,在一定条件下,以式(11)作为被控对象,对阻性负载、阻感负载和阻容负载都有很好的适应性。考虑到电压反馈系数Ku和PI控制器环节[见式(4)],电压环开环传递函数可表示为:
(12)
由工程设计法可得:
(13)

(14)

4性能分析
图3为开环控制测试结果。由图3可以看出,测试结果存在死区效应,在过零附近有畸变,THD=3.31%。如果存在扰动,则开环控制难以保证精度。

a为期望电压;b为实际输出电压; c为负载电流;调制比为0.9。 图3 开环控制测试结果
图4与图5分别为PI-P双环控制的输出波形和误差。双环控制下死区效应有改善,在THD=0.13%左右,基波峰值为312.2,过渡过程的最大误差为11.4,稳态误差在-1.6~1.6之间波动,正负峰值附近和电压过零前后误差较大。
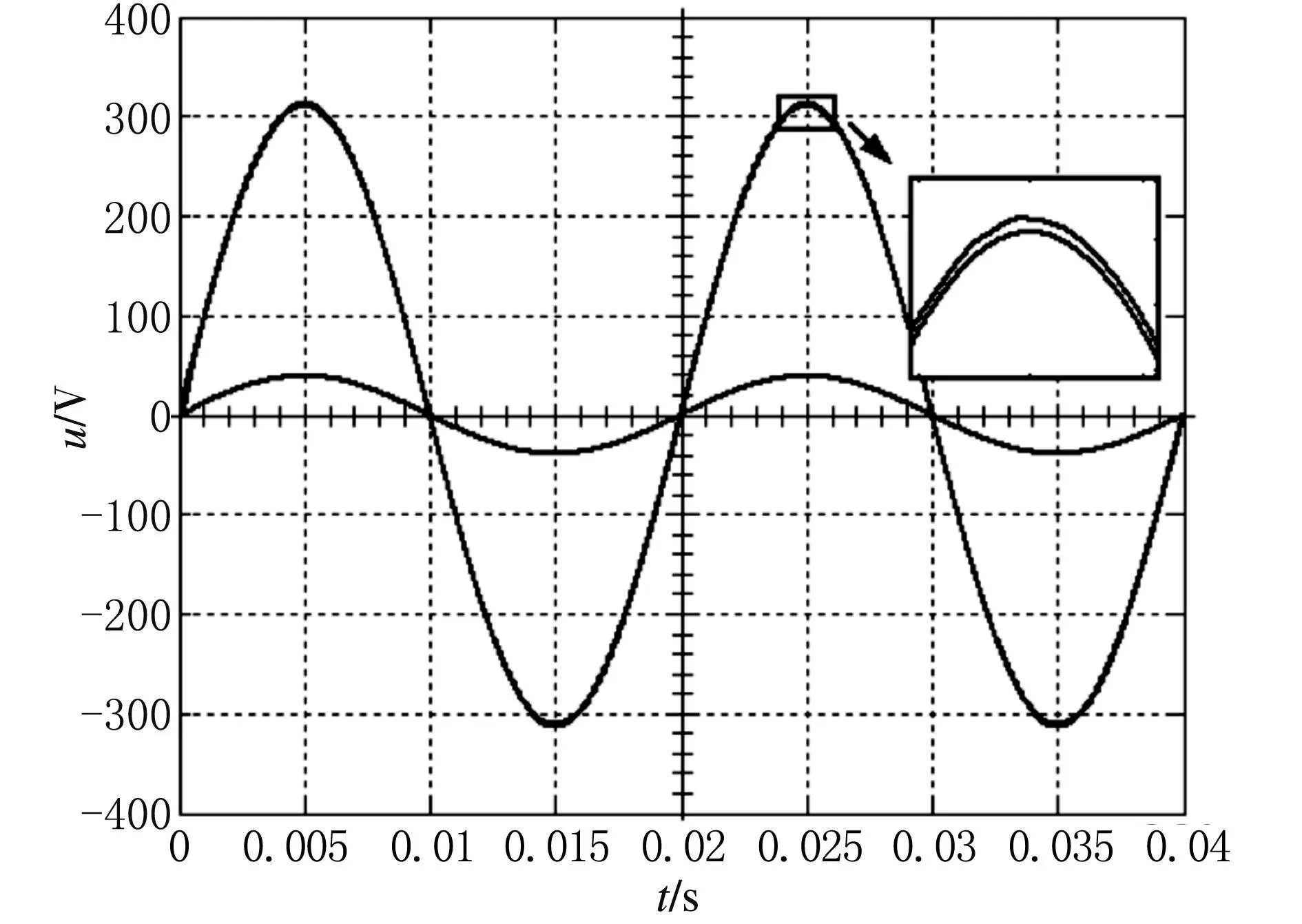
图4 PI-P双环控制输出波形
图6与图7分别为准PR-P双环控制的输出波形与误差。显然,死区效应有所改善,在THD=0.13%左右,基波峰值为311,过渡过程的最大误差为10.8,过零前后误差稍大,基本克服了稳态误差,输出波形比较稳定。

图5 PI-P双环控制输出误差

图6 准PR-P双环控制输出波形

图7 准PR-P双环控制输出误差
图8是准PR-P双环控制下75%负载变为100%负载的电压电流波形。由图8可以看出, 无论是75%负载还是100%负载,逆变器都有良好的稳态性能,负载切换瞬间电压有峰刺,但很快恢复,电流转换很平稳。
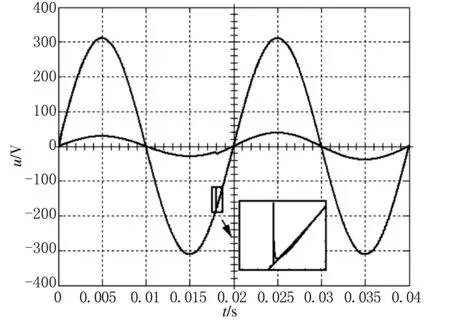
图8 准PR-P双环控制下75%负载变为 100%负载的输出波形
5结语
(1) 闭环控制在减小畸变、克服死区影响和提高精度等方面有优势。
(2) 电容电压和负载电流前馈补偿控制既有利于控制器设计,又能改善系统性能。
(3) 常规PI控制器对于交流输入不能做到稳态无静差控制,但在精度容许的情况下具有设计和实现简单的优势。有时候采用电压有效值反馈控制可以提高幅值精度,但纯幅值控制难以保证波形质量;瞬时值反馈可兼顾幅值、频率和相位。
(4) PR控制在理论上能够实现对交流输入的无静差控制,但实际应用时无论是用模拟器件还是用数字方法实现,均不易达到应有的精度要求[4]。准PR控制在稳态误差可控情况下,提高了对电网频率波动的鲁棒性。本文研究显示,准PR控制在精度上稍优于常规PI控制,但直流分量稍大,两者THD相当;PI控制输出误差稍大是相对于期望值而言的,波形很好。
(5) 采用优化算法设计控制器参数,可减少对系统模型的近似和简化,使结果更接近于实际,也可减少对专家经验的依赖。
(6) 由于优化设计通常是通过计算机仿真技术实现的,因此优化结果不必刻意追求最优解,次优解、满意解即可,而智能优化算法正好适用。实际应用中,可选取几个较好的优化解对比测试后选用。
参考文献:
[1]伍家驹.逆变器理论及其优化设计的可视化算法[M].北京:科学出版社, 2012: 171-195.
[2]杨会敏,宋建成.基于双环控制的单相电压型PWM逆变器建模与仿真[J].电气传动自动化, 2009, 31(1): 15-18.
[3]周樑.PWM逆变电源瞬时值反馈控制技术研究[D].武汉:华中科技大学, 2006.
[4]赵清林,郭小强,邬伟扬.单相逆变器并网控制技术研究[J].中国电机工程学报, 2007, 27(16): 60-64.
[5]朱军卫,龚春英.逆变器单极性电流SPWM控制与滞环控制比较[J].电力电子技术, 2004, 38(1): 26-29.
[6]Zmood D N, Holmes D G. Stationary Frame Current Regulation of PWM Inverters with Zero Steady-state Error [J].IEEE Transactions on Power Electronics, 2003, 18(3): 814-822.
[7]Shi Y, Eberhart R. A Modified Particle Swarm Optimizer[C]//Proceedings of IEEE International Conference on Evolutionary Computation. Anchorage, 1998: 69-73.
[8]Carlisle A, Dozier G. An Off-The-Shelf PSO[C]// The 2001 Workshop on Particle Swarm Optimization. Indianapolis, 2001: 1-6.
[9]张绪杰,李绍军,钱锋.基于共享机制的小生境粒子群优化算法[C]//沈阳:2005中国控制与决策学术年会论文集. 2005: 958-961.
[10]裴胜玉,周永权.基于Pareto最优解集的多目标粒子群优化算法[J].计算机工程与科学, 2010, 32(11): 85-88.
[11]Zhang J, Zhang J R, Li K.A Sequential Niching Technique for Particle Swarm Optimization[C]// 2005 International Conference on Intelligent Computing (ICIC 2005). Hefei, 2005:390-399.
[12]张航,王伟,郑玲,等.一种基于密度聚类的小生境差分进化算法[J].计算机工程与应用, 2008, 44(23): 42-45.
[13]林焰,郝聚民,纪卓尚,等.隔离小生境遗传算法研究[J].系统工程学报, 2000, 15(1): 86-91.
[14]谢华林,杨金明.基于SABER仿真器的双管正激参数及控制环路的设计[J].电源技术应用, 2009, 12(10): 8-11, 25.
[15]陈伯时.电力拖动自动控制系统:运动控制系统(第3版)[M].北京:机械工业出版社, 2003: 68-71.
(责任编辑:王长通)
Study on Parameters Optimization of Quasi-PR Controller for
SPWM Inverter Using Niching PSO Algorithm
WANG Yong-lin1, AI Ming2, QU Bo-yang1
(1. Zhongyuan University of Technology, Zhengzhou 450007;
2. Shengda Trade Economics and Management College of Zhengzhou, Zhengzhou 451191, China)
Key words:SPWM; inverter; niching algorithm; particle swarm optimization; quasi-PR control; LCL filter


