移动最小二乘法在高阶连续问题数值模拟中的应用

移动最小二乘法在高阶连续问题数值模拟中的应用

陈根生， 杨子胜， 孙玉周

(中原工学院, 郑州 450007)

摘要：以弯曲梁为例，应用移动最小二乘法构造具有高阶连续特征的形函数，建立无网格数值计算框架。研究移动最小二乘法在传统弯曲梁和高阶连续弯曲梁数值模拟中的应用，并对施加边界条件等相关关键问题进行讨论。

关键词：弯曲梁；高阶连续；移动最小二乘法；无网格法；罚数法

中图分类号：TU53

文献标志码：A

DOI:10.3969/j.issn.1671-6906.2015.03.019

Abstract:The shape function with the high-order continuum is constructed with the moving least-square method, and a mesh-free computational scheme is then established for the bending beams. The proposed method is used to investigate the application of the moving least-square approximation in the numerical simulation of the classical bending beam and high-order continuum bending beam. Some key issues such as the imposition of the boundary conditions are studied and discussed.

收稿日期：2014-03-10

基金项目：河南省科技攻关计划项目(122102210492)

作者简介：朱付保(1974-)，男，河南柘城人，副教授，博士，主要研究方向为智能信息处理，空间数据库、地理信息系统、数据挖掘。

文章编号：1671-6906(2015)03-0085-05

对于传统的连续梁来说，曲率是一个基本变量，它被近似为横向位移的二阶导数。在应变梯度连续理论[1-2]、偶应力理论[3]等高阶连续理论中，需要考虑位移的二阶导数。在微/纳机电系统中，经常把元器件处理为高阶连续梁[4-6]，这时需要考虑挠度的三阶甚至更高阶的导数。高阶连续问题给数值模拟带来新的挑战，利用有限元法构造高阶连续形函数需要做大量工作[7]。通过应用适当的基函数和权函数，利用移动最小二乘法可以很容易地构造出具有高阶连续特征的形函数[8-9]，位移的高阶导数可以直接用节点位移来近似，给数值离散带来很大的方便。但是，它也带来一些新的问题，比如，在数值计算中，高阶应变不再是显式的变量。如何基于位移高阶导数施加转角约束，如何施加高阶面力边界条件，都是人们面临的新的问题。本文以弯曲梁为例，研究移动最小二乘法在高阶连续问题数值模拟中的应用，并讨论如何施加边界条件等。

1移动最小二乘法

(1)

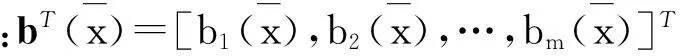
对于本文研究的弯曲梁问题，选用的一维三次基函数为：

(2)

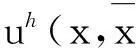
(3)

式中：wI(x-xI)是权函数，当x在xI影响域内部时，wI(x)>0；当x在xI影响域的边界和外部时，wI(x)=0。

对(3)式求导：

=0,j=1,2，…,m

(4)

令

B(x)=[w1(x)b(x1)w2(x)b(x2)…wN(x)b(xN)]

(5)

移动最小二乘法的形函数[8-9]可以计算为：

(6)

令

(7)

形函数φ(x)的1～3阶导数可计算为：

(8)

权函数w(x)在移动最小二乘近似中具有很重要的作用，它在节点xI处的值最大，并且具有紧支撑性，即当r=‖x-xI‖/dmI>1时,w(r)=0,dmI为每个节点控制的支撑域直径。本文采用三次样条权函数[8-9]，即

(9)

图1为移动最小二乘法形函数和它的1、2阶导数的图像。

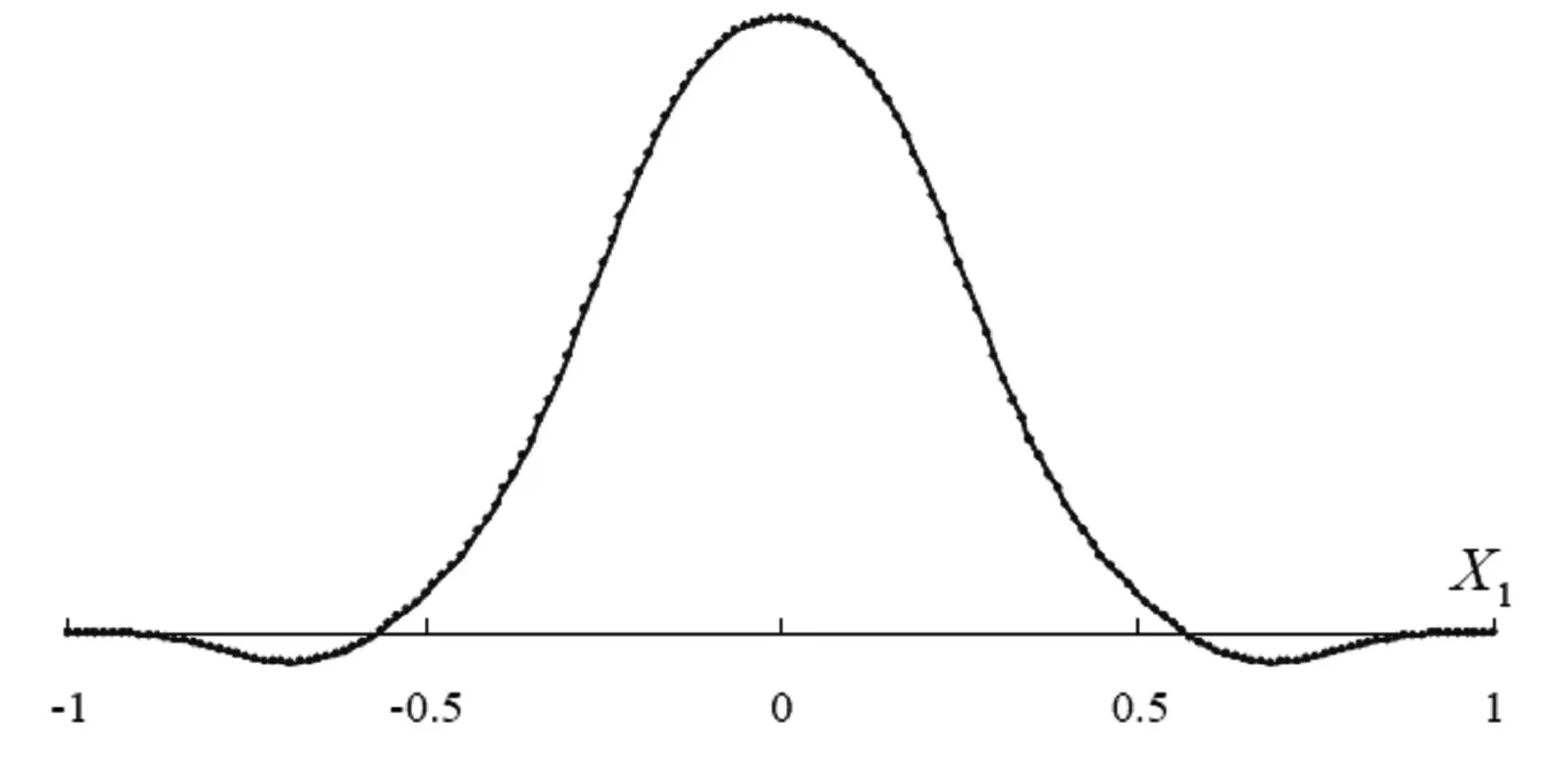
(a)形函数φ

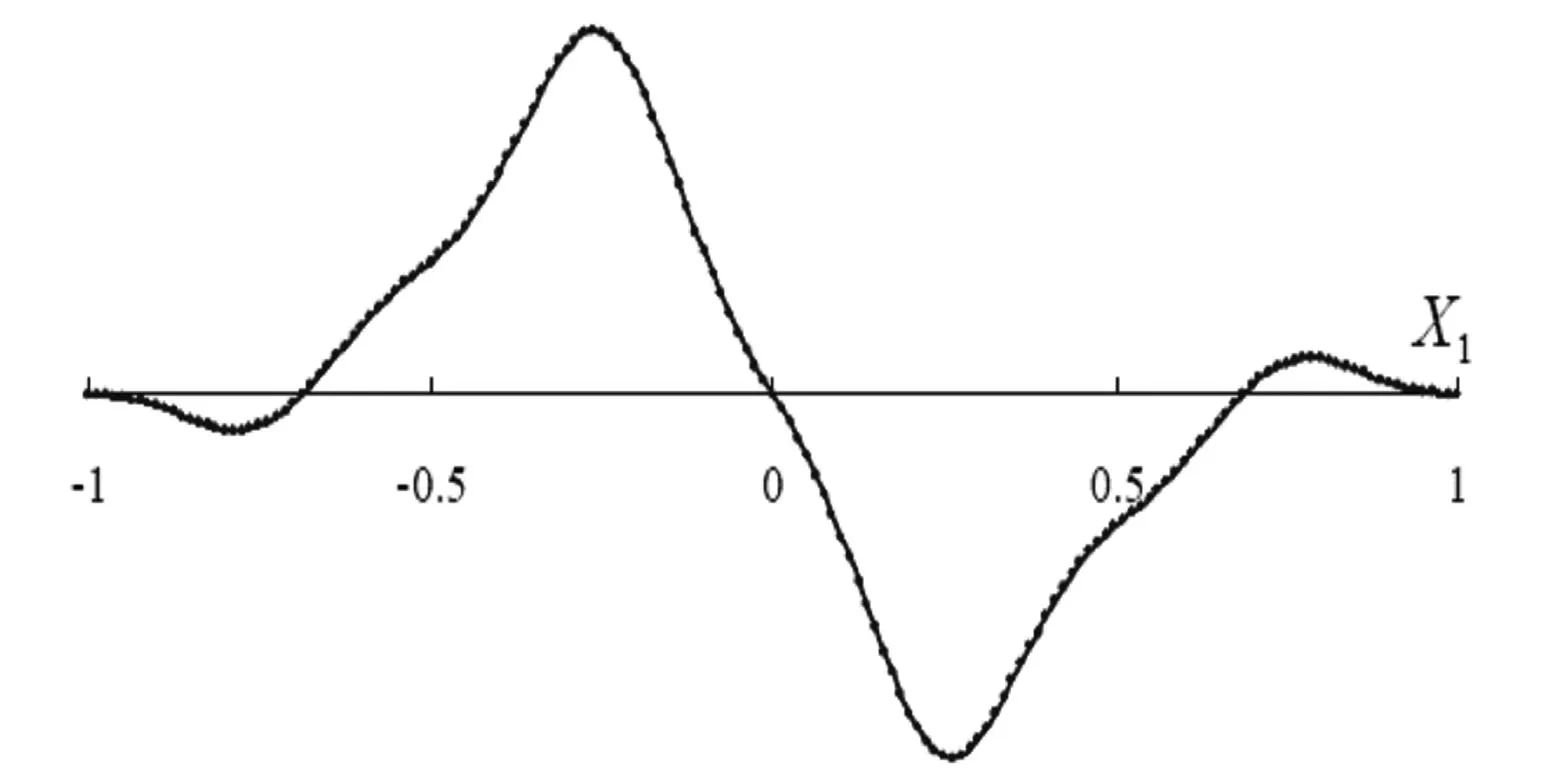
(b)一阶导数φ ,x

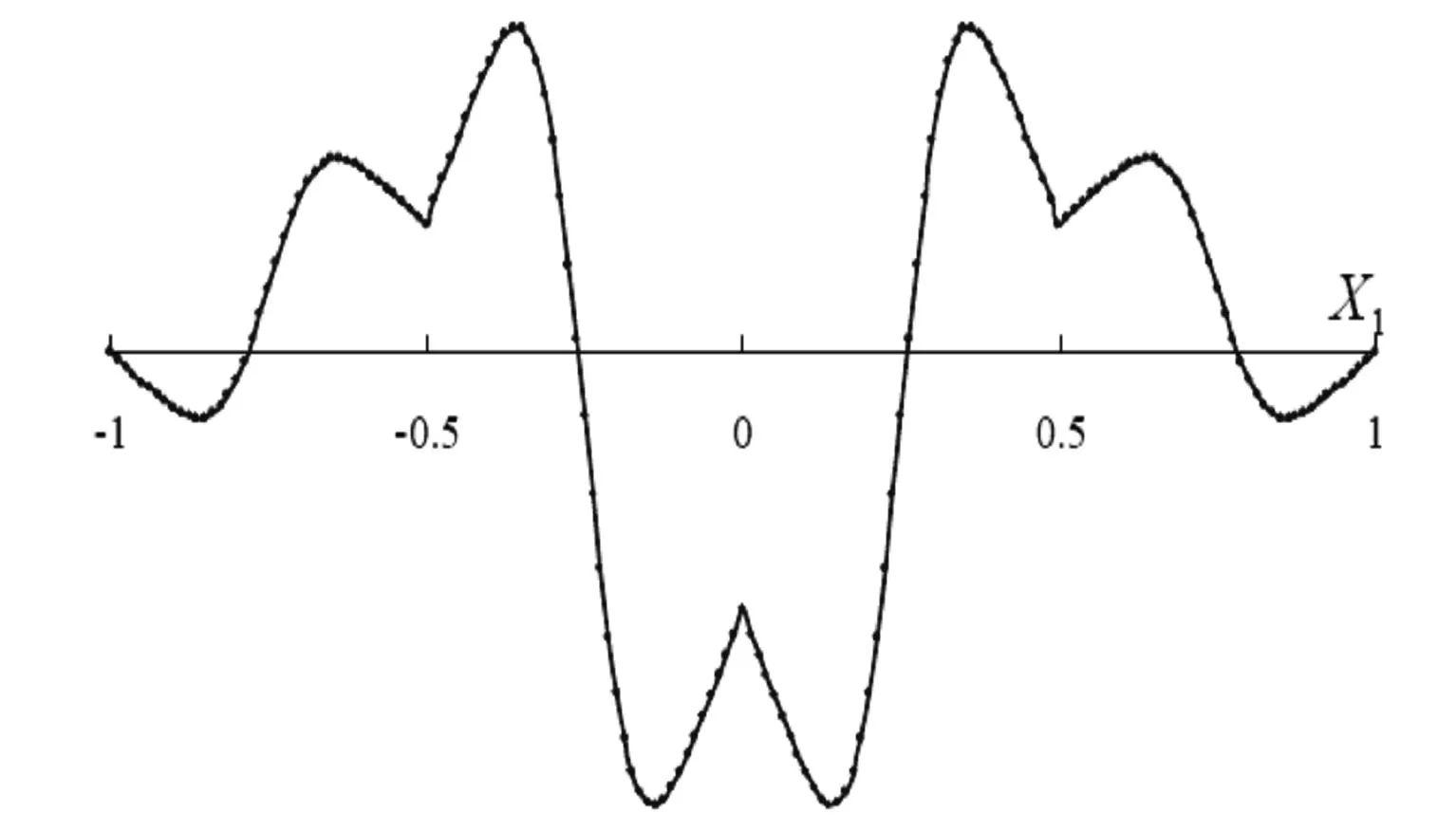
(c)二阶导数 φ ,xx 图1　移动最小二乘法形函数及其导数

2传统弯曲梁的无网格法

图2为一个简支梁模型，在有限元方法中，经常把转角θ处理为节点变量，曲率由节点的挠度和转角插值得出[7]。

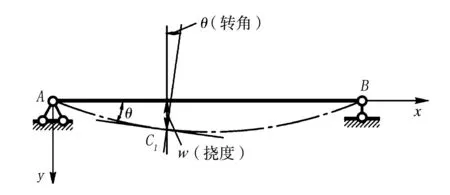
图2　简支梁模型

考虑到移动最小二乘法形函数具有高阶连续性，本文把梁的应变能表示为：

(10)

挠度的二阶导数直接用节点的挠度插值，即

(11)

其中：w,xx为挠度的二阶导数；φI,xx为移动最小二乘法形函数的二阶导数；wI(x)为节点挠度；n为计算点影响域内的节点数。

由于转动惯量I=∫Ay2dA，式(10)可以变为：

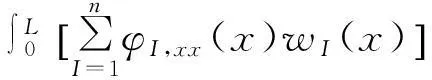
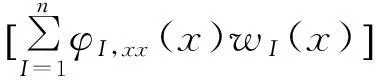
(12)

弯曲梁刚度矩阵可计算为：

(13)

在计算刚度矩阵时，积分区间的布置与节点的布置分别独立进行，为了方便计算，本文中积分区间的布置与节点的布置一致(相邻两节点确定一个积分区间)，然后应用高斯积分法对每个积分区间进行积分。通过求解下列方程组可以得到节点的挠度:

KU=F

(14)

其中:U为节点挠度向量(不包含节点转角)；F为节点力矢量。

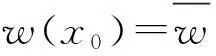
(K+Kp)U=F+Fp

(15)

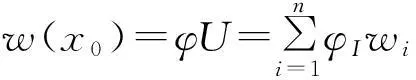
(16)

罚数α可被取为比刚度矩阵元素大5～6个量级的正数。

对于转角边界条件，将转角用节点挠度和形函数的一阶导数插值后，可由罚数法来施加。

用一个简支梁的例子验证方法的收敛性和精度。假设图2中简支梁的跨中受集中力F作用，梁截面高度h=1m，厚度b=0.01m，梁中点挠度δ可以采用经典力学方法计算为FL3/48EI。为了验证节点数量对结果的影响，每个积分单元布置3个高斯点，节点的影响域半径定为3.0。表1所示为不同节点数时梁中点挠度值。

表1　不同节点数时梁中点挠度值　10 -4 m

由表1可以看出，所得结果收敛性很好。为了分析影响域大小对计算结果的影响，固定梁上节点数为61，节点的影响域半径(R=Dmax(xj+1-xj))从2.0(xj+1-xj)变化到5.0(xj+1-xj)。

梁中点挠度值如表2所示。

表2　不同D max数值时的梁中点挠度值　10 -4 m

由表2可以看出,Dmax取3.0时可以得到最好的结果。

对图3所示的两个悬臂梁进行计算。

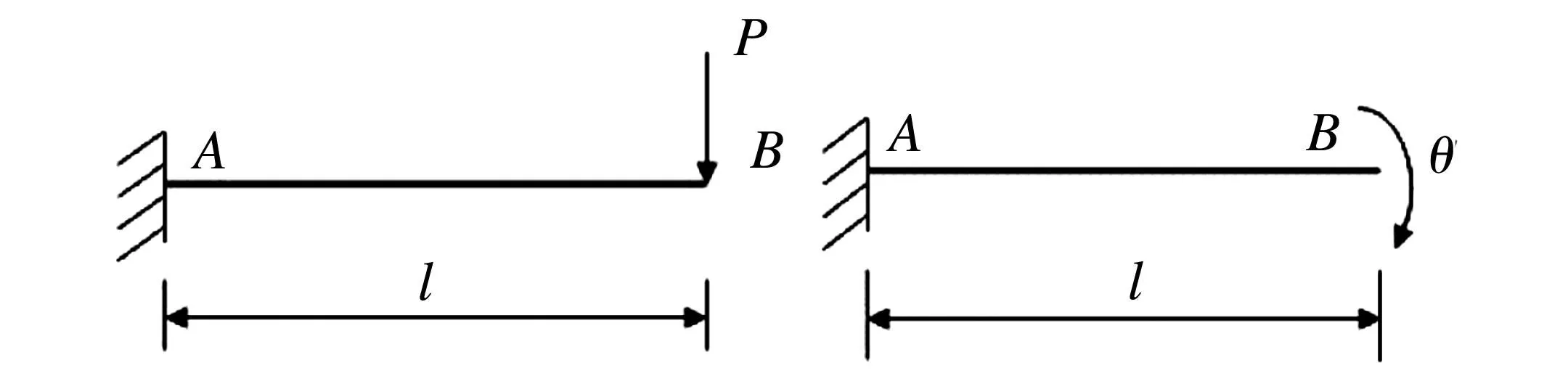
(a)受集中力的悬臂梁 　　(b) 受角位移的悬臂梁 图3　悬臂梁计算简图

梁在自由端分别受集中力和角位移作用，角位移用罚数法施加，梁的横截面尺寸均为0.6m×0.6m，集中力P=100kN，角位移θ=0.1rad，梁的长度l=5m，弹性模量E=2.06×1011Pa，梁上布置的节点数固定为101。图4为梁的挠度和转角随横截面位置的变化曲线。

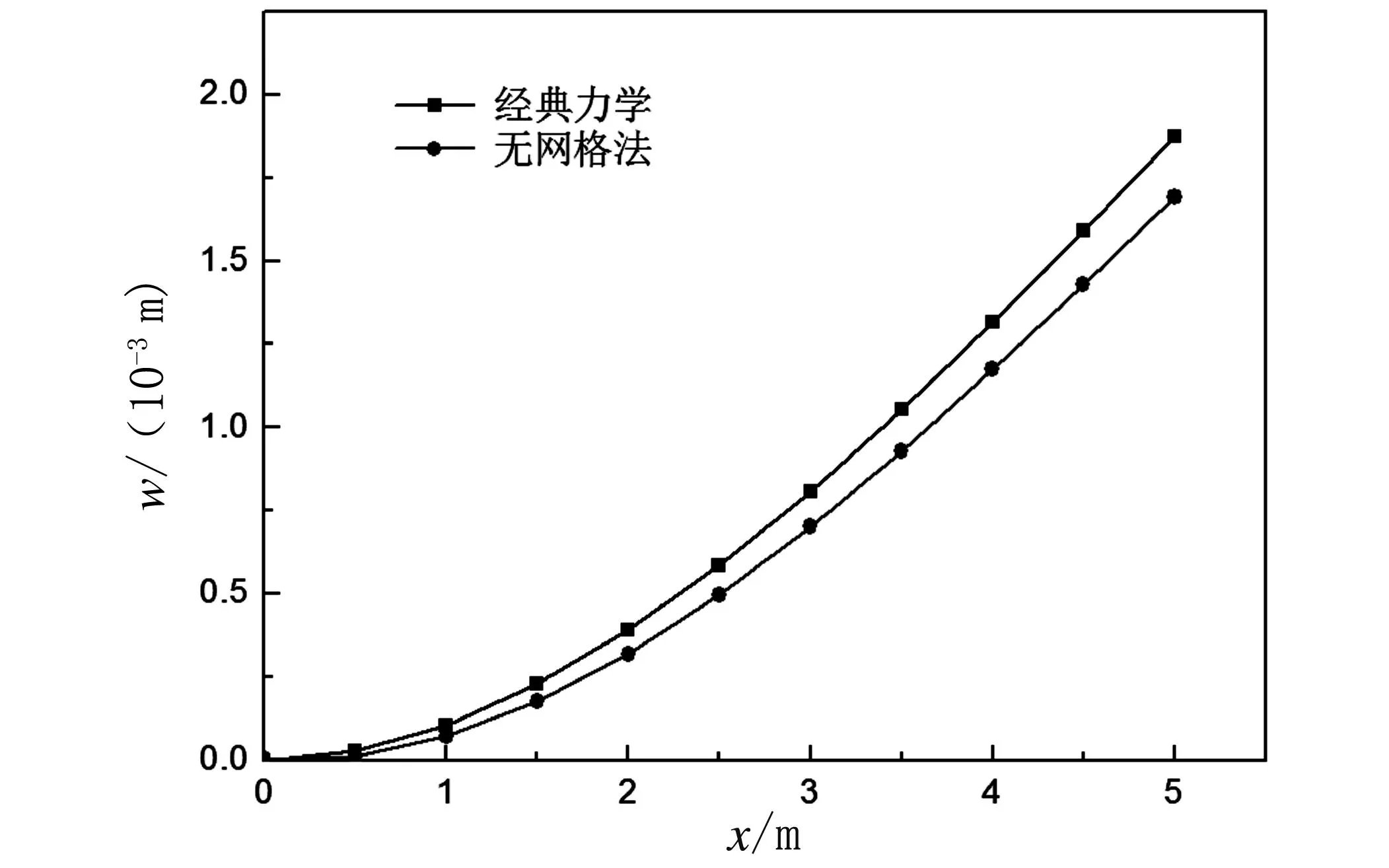
(a)受集中力作用的悬臂梁挠度曲线

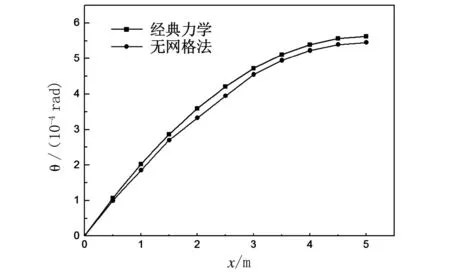
(b) 受集中力作用的悬臂梁转角曲线

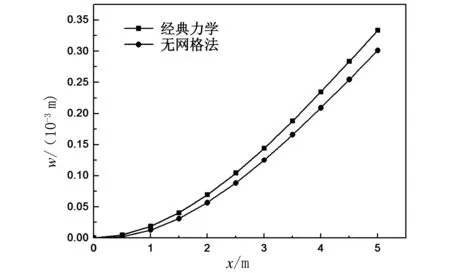
(c)受角位移作用的悬臂梁挠度曲线

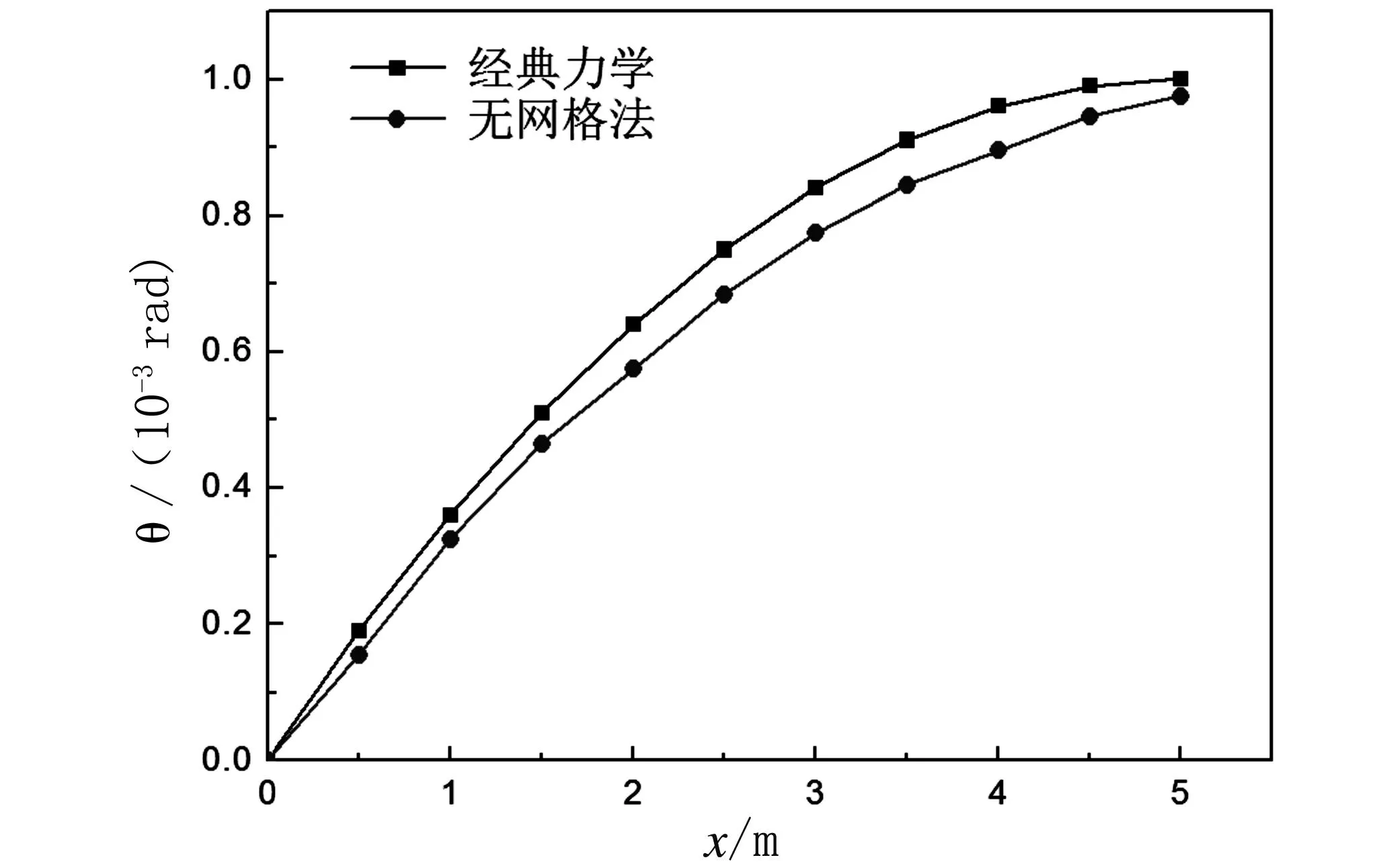
(d)受角位移作用的悬臂梁转角曲线 图4　弯曲梁的挠度曲线和转角曲线

由图4可以看出，本文得到的挠度和转角与经典力学的计算得到的结果相符较好，说明用罚数法施加位移边界条件和转角边界条件均可取得很好的效果。

3高阶连续梁的无网格法

在高阶连续梁模型中，梁的应变和高阶应变[4-5]分别定义为：

(17)

应力和高阶应力定义为：

σxx=Eεxx+lxεxxx,τxxx=g2Eεxxx+lxEεxx,

τyxx=g2Eεyxx

(18)

式中:E为弹性模量;g和lx分别为高阶连续梁的体本征尺寸影响因子和面本征尺寸影响因子。

应变能可以表示为：

(19)

式中，A表示梁的横截面。

对于高阶连续梁，出现了挠度的三阶导数，本文直接将其近似为：

(20)

高阶连续梁的刚度矩阵计算为：

(21)

可以采用类似于本文上述方法建立无网格计算框架，数值计算直接给出节点的挠度值。

下面通过数值计算分析尺寸因子产生的影响。构建一个简支梁，其高度等于厚度(h=b)，梁上布置的节点总数固定为61，决定节点的影响域半径固定为3.0，边界条件的施加与本文上述方法相同。分析尺寸因子g的影响时，固定尺寸因子lx为0.001 25b，令g从0变化到5.0。从图5可以看出，随着g值的不断增大。其对计算结果的影响不断增大。图5中纵坐标为梁中点挠度相对于传统力学结果(两个尺寸因子均为0)的相对变化量。分析尺寸因子lx的影响时，将尺寸因子g固定为0.187 5b，令lx从0变化到0.8。从图6可以看出，当lx值在某一范围内时，对计算结果有较大的影响。图6中纵坐标同样为梁中点挠度相对于传统力学计算结果的相对变化量。

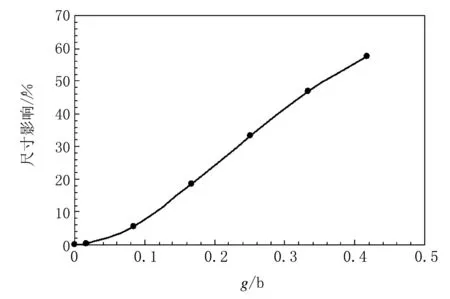
图5　尺度影响因子g对结果的影响

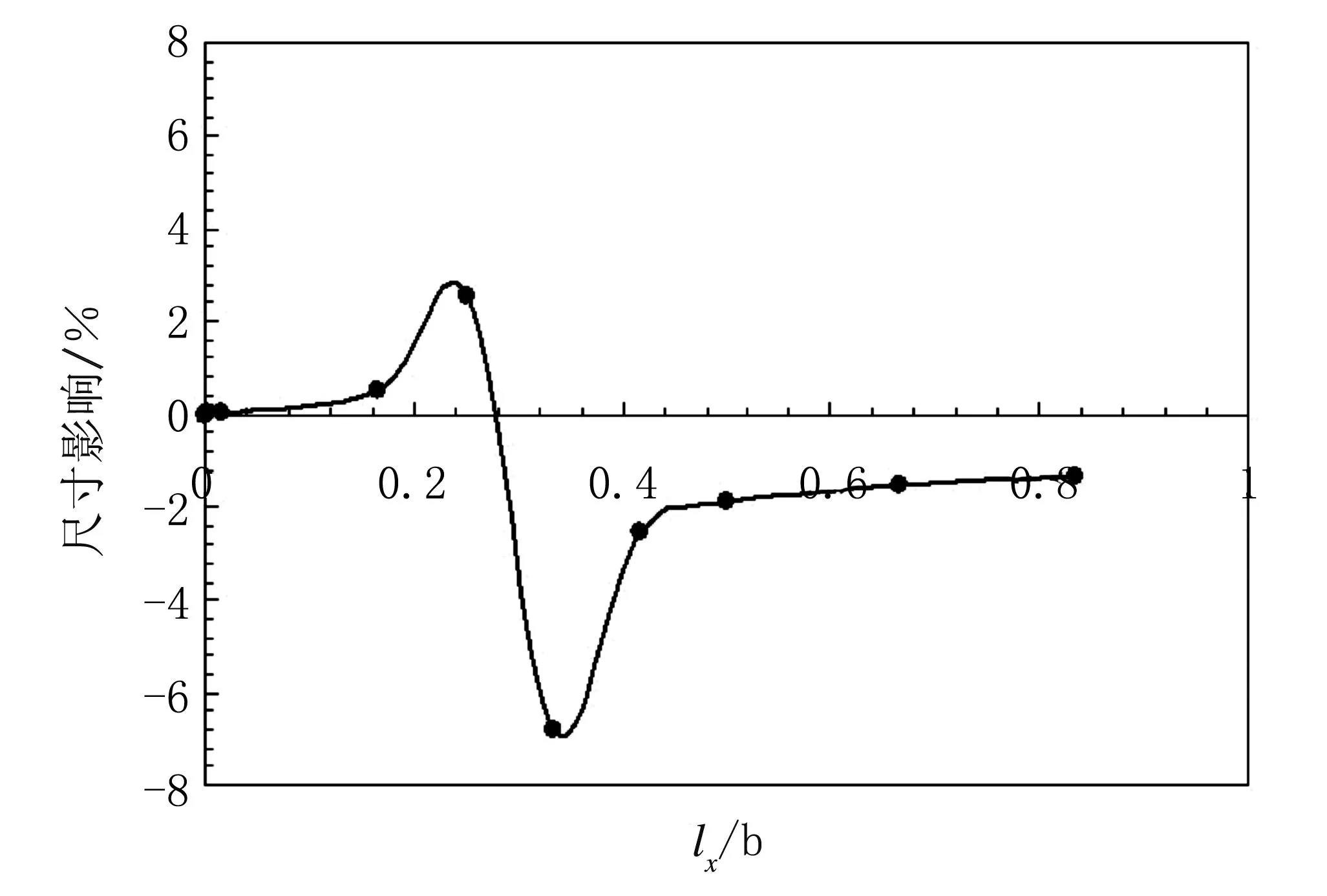
图6　尺度影响因子lx对结果的影响

4结语

高阶连续问题中出现了位移的高阶导数，给有限元法等传统数值方法带来了很大麻烦。本文应用移动最小二乘法构造具有高阶连续特征的形函数，位移的高阶导数直接由节点位移插值得到，可以方便地建立无网格计算框架，数值计算结果说明本文的方法有效。

在数值执行中，节点位移直接通过求解方程组得到，任一位置的转角可基于节点位移插值得到。由于转角为位移的一阶导数，转角边界条件可以较方便地通过罚数法来施加。对于高阶连续问题中的高阶面力等复杂边界条件，由于可以表示为位移导数的函数，所以也可以用罚数法来施加，这将在后续的工作中进行研究。

参考文献:

[1]XiaZC,HutchinsonJW.CrackTipFieldsinStrainGradientPlasticity[J].JournalofMechanicsPhysicsofSolids, 1996(44): 1621-1648.

[2]FleckRD,HutchinsonJW.StrainGradientPlasticity[J].AdvancedAppliedMechanics, 1997(33): 295-361.

[3]ToupinRA.ElasticMaterialswithCoupleStresses[J].Arch.Ration.Mech.Anal., 1962(11): 385-414.

[4]CivalekO,DemirC.StrainGradientElasticityandModifiedCoupleStressModelsforBucklingAnalysisofAxiallyLoadedMicro-scaledBeams[J].InternationalJournalofEngineeringScience, 2011(49): 1268-1280.

[5]CivalekO,DemirC.BucklingandBendingAnalysesofCantileverCarbonNanotubesUsingtheEuler-BernoulliBeamTheorybasedonNon-localContinuumModel[J].AsianJournalofCivilEngineering, 2011(12): 651-661.

[6]李志宏. 微纳机电系统 (MEMS/NEMS) 前沿[J].中国科学, 2012, 42(12): 1599-1615.

[7]梁醒培, 王辉. 应用有限元分析[M]. 北京：清华大学出版社，2003.

[8]BelytschkoT,KrongauzY.MeshlessMethod:anOverviewandRecentDevelopments[J].Comput.MethodsAppl.Mech.Engrg., 1996(139): 3-47.

[9]BelytschkoT,LuYY,GuL.Element-freeGalerkinMethods[J].InternationalJournalforNumericalMethodsinEngineering, 1994(37):229-256.

[10]SunYZ,LiewKM.BendingBucklingofSingle-walledCarbonNaotubes:HigherOrderGradientContinuumandMesh-freeMethod[J].ComputerMethodinAppliedMechanicsandEngineering, 2008(197): 3001-3013.

[11]SunYZ,LiewKM.ApplicationoftheHigh-orderCauchy-BornRuleinMesh-freeContinuumandMultiscaleSimulationofCarbonNanotubes[J].InternationalJournalforNumercalMethodsinEngineering, 2008, 75(10): 1238-1258.

(责任编辑：姜海芹)

The Application of the Moving Least-square Approximation in the

Numerical Simulation of the Higher-order Continuum Problems

CHEN Gen-sheng， YANG Zi-sheng, SUN Yu-zhou

(Zhongyuan University of Technology，Zhengzhou 450007, China)

Key words:bending beam; higher-order continuum; moving least-square approximation; mesh-free method; penalty method