基于剪切波变换与直觉模糊PCNN模型的图像融合方法

E-mail:trusen@qq.com

基于剪切波变换与直觉模糊PCNN模型的图像融合方法

张耀军，栗磊，吴桂玲

(信阳农林学院计算机系，河南信阳464000)

摘要：针对传统图像融合方法计算复杂度高、运行机制过于机械的问题，提出了一种基于剪切波变换(ST)与直觉模糊-脉冲耦合神经网络(IF-PCNN)模型的新型图像融合方法.利用ST优越的图像信息捕捉性能对源图像进行多尺度多方向分解，对经典PCNN模型进行改进，赋予IF性能形成IF-PCNN新型模型，并对低频子带图像和一系列高频子带图像进行融合，最后采取ST反变换获得最终融合结果图像.仿真结果表明，同现有的几种经典融合方法相比，文中提出的方法在主客观评价过程中均具有显著的优势.

关键词：剪切波变换；脉冲耦合神经网络；直觉模糊；图像融合

收稿日期：2014-12-20;修改稿收到日期:2015-02-13

基金项目:河南省基础与前沿技术研究计划资助项目(132300410452)

作者简介：张耀军(1979—)，男，河南信阳人，讲师，硕士.主要研究方向为网络信息安全与图像智能信息处理.

中图分类号：TP 391.41文献标志码：A

Technique for image fusion based on shearlet transform and

intuitionistic fuzzy pulse coupled neural networks

ZHANG Yao-jun，LI Lei，WU Gui-ling

(Department of Computer Science,Xinyang College of Agriculture and Foresty,Xinyang 464000,Henan,China)

Abstract:In order to settle the drawbacks including high computational complexities and the unreasonable mechanism of traditional image fusion methods,a novel technique for image fusion based on shearlet transform(ST) and intuitionistic fuzzy pulse coupled neural networks(IF-PCNN) is proposed in this paper.Due to the better competence of image information capturing,ST is utilized to conduct the multi-scale and multi-directional decompositions of source images.In addition,by combining the IF characteristic,the classic PCNN model is improved to be IF-PCNN,which is responsible for the fusion of low-frequency sub-images and a series of high-frequency ones,respectively.Finally,the final fused image can be obtained by using inverse ST.Compared with current typical techniques,the results demonstrate that the proposed one has remarked superiorities in terms of both subjective and objective evaluations.

Key words:shearlet transform;pulse coupled neural network;intuitionistic fuzzy;image fusion

由多传感器获取的关于同一场景的不同图像，通常拥有大量的互补信息和冗余信息[1-2].对条件不佳场景下的可见光图像和红外图像来说，可见光图像擅长对场景中的环境和背景信息加以描述，画面纹理清晰；而红外图像则侧重于对场景中的热源信息进行描述，着重把握和捕捉红外辐射信息突出的目标.因此，对不同类型图像传感器获取的关于同一场景的不同图像进行融合是非常有必要的.

与小波变换[3]、脊波变换[4]和轮廓波变换[5-6]等几种经典的变换域方法相比，剪切波变换(Shearlet transform, ST)[7-9]无论在图像信息捕捉能力，还是算法计算复杂度方面均具有显著的优势，并逐渐成为图像融合领域的主流方法和研究热点，并且ST也已被广泛应用于图像融合、图像特征提取等领域.而作为第三代人工神经网络模型中的典型代表，脉冲耦合神经网络(Pulse coupled neural networks,PCNN)[10]因具有优越的同步脉冲发放特性，也被广泛应用于图像处理领域.

目前，PCNN模型已大量应用于图像去噪、图像分割和图像融合等领域中，PCNN模型中大量待定参数的存在和异常复杂的运行机制成为其性能提升的瓶颈.针对此问题，国内外大量学者对经典PCNN模型进行了结构上的改进，产生了一系列新型图像处理方法[11-15].然而，PCNN模型中的非0即1的机械式脉冲输出方式的改进却鲜有报道.针对此问题，文中将直觉模糊(Intuitionistic fuzzy, IF)[16]机制引入PCNN模型，构建IF-PCNN模型.另外，将ST引入文中提出的图像融合方法，利用其完成源图像的多尺度和多方向分解，各生成一幅低频微观子带图像和一系列高频微观子带图像.然后，由IF-PCNN完成对应微观子带图像的融合过程.最后，采用ST反变换生成最终融合结果图像.

1ST基本模型

Guo等构造了合成膨胀下的仿射系统模型，并提出在维数n=2条件下的系统表达公式[17]299：

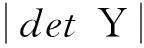
令φ∈L2(R2)满足下列条件[17]300：

其中，φ*为函数φ的傅氏变换;ξ,ξ1,ξ2为自变量;φ1和φ2分别满足[17]300：

每一个剪切波位于近似大小为22j×2j、线方向斜率为2-jl的梯形对上(图1(a)).根据小波理论，由一维小波张成的二维小波基具有正方形的支撑区间，在尺度j，其近似边长为2j(图1(b)).当尺度j变大时，小波支撑基的面积随之变大，但是由于其无方向性，非零的小波系数以指数形式增长，导致大量不可忽略的系数出现.小波逼近奇异曲线最终表现为“点”逼近过程，而非原曲线最优的稀疏表示.剪切波以近似长条形即梯形对去逼近曲线，当尺度j变大时，其支撑基的线方向斜率2-jl也随之变化，使得这种近似长条形的支撑基具有各向异性，能够有效捕获方向信息，它是图像中边缘等特征的真正的稀疏表示.图2给出了剪切波变换中的频率分割示意.

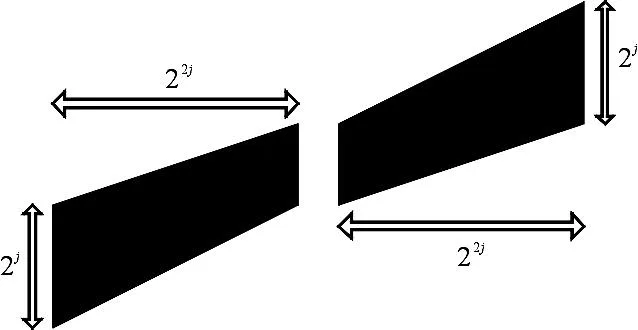
( a) ST的梯形支撑区间

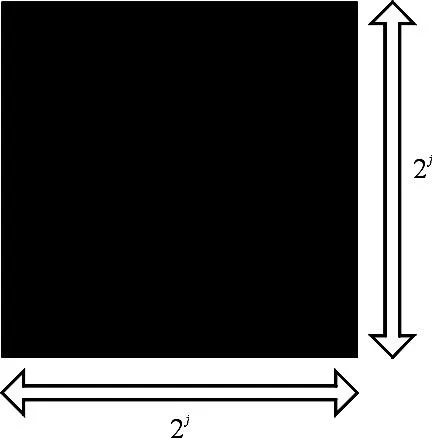
( b)二维离散小波的支撑区间

图2　 ST频率分割示意

2直觉模糊PCNN模型

经典PCNN模型拥有大量的待定参数和复杂的运行机制，虽然该模型具有丰富的生物学背景，但在很大程度上，图像处理的最终效果仍然主要取决于待定参数的设置是否合理，而参数的设置又常常需要依靠研究者的主观经验和多次实验调试结果来实现，因此，对经典的PCNN模型进行适当的改进是非常有必要的.文中提出一种直觉模糊PCNN(IF-PCNN)模型，该模型主要进行3个方面的改进：① 对馈送域输入F进行改进，由综合空间频率(Spatialfrequency,SF)来决定；② 对链接强度β进行改进，变换为由改进型拉普拉斯算子(ImprovedLaplacianoperator, OIL)来确定；③ 彻底改变以往模型中神经元输出状态非0即1的极端状态，取而代之的是一种以直觉模糊隶属度和非隶属度自适应决定的动态输出机制[11].

2.1馈送域输入F的改进

由于图像中重要目标信息的像素灰度值，往往与其周围的像素点信息存在明显的差异，而图像的FS[18]反映了一幅图像中像素点的活泼指数，FS数值越大表明像素点越活泼突出.因此，可以考虑由每个像素点对应的综合FS数值来代替馈送域输入.FS的数学表达式为

针对图像I(i,j)，FR,FC,FMD与FSD的表达式分别为

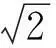
显然，根据(6)～(9)式，可以很容易计算出图像中每一个像素点的FS值，FS越大表示对应点相对周围4个方向的像素点更为活跃和突出，即该像素点具有更为丰富的信息.

输入F改进后具有以下优势：① 传统经典PCNN模型馈送域输入项目过多，涉及到大量参数，而用综合FS来代替原始的馈送域输入，不仅可以更直接、更精确地描述像素点内在特征信息，而且可以减少参数的设置；② 综合FS收集了像素点水平方向、垂直方向、主对角线方向与副对角线方向的梯度信息，摒弃了以往仅考虑单个像素点灰度值的情况，评价更加客观；③ 高频微观子带图像中通常涉及大量负系数，传统PCNN模型无法处理馈送输入域为负数的情况，而综合FS的结果始终为非负，避免了传统模型的缺陷.

2.2链接强度β的改进

传统PCNN模型中的参数β，决定了内部连接项U中馈送输入域F与链接输入域L的成分之比.β的数值越大，链接输入L在U中所占的比例就越大.将链接强度β赋予一个常数的方法虽然较为简单，但忽视了相邻神经元之间的相互联系，未能充分利用链接输入域为神经元提供的信息.因此，文中提出采用改进型拉普拉斯算子OIL来确定链接强度β.

OIL的数学表达式为

OIL记录了中心像素点的拉普拉斯能量，OIL的数值越大，代表该像素点的能量越高;反之，则代表相应能量越低.因此，可以用OIL的数值作为链接强度β的数值，即

其中r为邻域半径，通常邻域取作一个正方形区域，且n为一个不小于3的奇数.

链接强度β改进后具有以下优势：① 摒弃了以往链接强度值设置较为随意的问题；② 通过收集中心像素点与相邻像素点间的灰度值差异，自适应地确定链接强度的数值.

2.3输出机制的改进

传统经典PCNN模型的输出机制仅将神经元的状态划分为点火与不点火两种状态，这种划分方式过于粗糙，仅仅考虑了两种极端情况，未能清晰地描述未点火神经元未来的点火趋势.为了精确地刻画每个神经元的点火趋势，文中提出采用直觉模糊集中的隶属度函数加以描述.其中，隶属度函数定义为

其中，i,j表示每个神经元对应的空间位置;μ为隶属度函数;U为内部连接项;θ表示阈值；n为迭代次数.当内部连接项U小于阈值θ时，隶属度函数μij等于Uij/θij，显然，隶属度函数μ小于1，此时神经元不点火，但隶属度函数μij的大小反映了该神经元的点火趋势，输出值Yij=Uij/θij；反之，当内部连接项U大于等于阈值θ时，神经元将立即点火，此时隶属度函数μ为1，且输出值Yij=1.

改进后具有以下优势：传统经典PCNN模型只能区分点火和不点火两种状态，而改进输出机制后的模型,可以清晰表达和度量神经元距离点火状态的潜在差距，在描述上更加细化.

3基于Shearlet与IF-PCNN模型的图像融合算法

通过改进传统经典PCNN模型，IF-PCNN模型的数学表达式如下：

其中，Lij为链接域输入；Wijkl为权值矩阵；αθ为衰减系数；Vθ为瞬变阈值.

与经典PCNN模型相比，IF-PCNN模型的运行机制更为直观、简洁，待定参数也由以前的9个缩减为3个，大大简化了运行机制，减少了运行过程中主观不确定因素的干扰.

① 采用ST理论获得一系列多尺度、多方向下的微观子图像；② 利用构建的IF-PCNN模型实现对应尺度、对应方向的微观子图像的融合过程；③ 进行ST反变换获得最终结果.这里，以2幅待融合源图像A和B为例，其中A和B为关于同一场景的不同图像传感器获取的已完成配准的源图像.图像融合过程如图3所示.

图3　基于 ST与 IF- PCNN模型的图像融合过程

图3中,low和high分别代表低频微观融合子图像和高频微观融合子图像部分;ST表示剪切波变换;I表示最终融合图像.

基于Shearlet与IF-PCNN的图像融合算法具体步骤如下：

1)ST将源图像A,B分解为低频微观系数{AS,0,BS,0}和高频微观系数{AS,L,BS,L}，其中，尺度级数为S，L是S下的方向分解级数.

2)分别计算低频微观系数和高频微观系数的综合FS数值，并将其作为IF-PCNN模型中的馈送域输入F的数值.

3)分别将高、低频微观系数子带图像的OIL作为链接强度β的数值.

4)根据(13)～(17)式运行IF-PCNN模型，并依据点火次数完成高、低频微观子图像的融合过程：

其中Nfire为点火次数.

5)利用ST反变换对融合后的低频微观子带融合图像和一系列高频微观子带融合图像进行处理,获取结果图像I.

图4给出了文中算法关于多聚焦图像的仿真实例.从图4可以看出，基于文中算法的仿真图像对原始图像具有很好的融合性能.

图4　仿真实例

4仿真实验

选取2组已配准图像作为待融合源图像进行文中方法的性能验证实验,以Windows 7系统和Matlab 2012为平台，仿真、比较与分析包括文中方法在内的几种融合方法的融合效果.

2组源图像分别为一对多聚焦图像和一对多波段遥感图像(图5)，这2组图像均含有256级灰度级，且图片大小均为512×512像素.在多聚焦图像组，第一幅图像中左侧区域较为清晰，可以清楚地看见“FOR BEST TASTE”的标识，但右侧区域较为模糊，凭肉眼已经无法辨识其中的信息；在第二幅图像中，情况完全相反，右侧区域中的“ES Magnifier Quality”标识非常清晰，而左侧区域的标识却无法辨清.在多波段遥感图像组中可以发现，2幅源图像分别侧重于不同信息的描述和表达，两者均拥有相当丰富的冗余和互补信息.

在融合仿真实验中，文中方法的参数设置为：ST多尺度分解级数为3层，方向分解级数由粗至细分别为10,10和18，邻域空间半径r=3，

图5　仿真源图像

αθ=0.2,Vθ=20,迭代次数n=200.为了与文中方法作比较，选取了另外3种方法，分别为多通道PCNN方法(方法1)[19]、ST方法(方法2)[20]与拉普拉斯变换方法(方法3)[21].为了保证融合效果的公正客观性，方法1～3中的参数仍沿用相关文献中的设置模式.融合结果除采取主观评价外，还选取了信息熵(EI)、互信息量(IM)[22]、空间频率(fS)以及加权融合质量指数(QWF)[23]4种客观评价指标作为评价依据.EI数值表征图像中包含信息量的大小，数值越大，融合图像信息越丰富.IM数值反映了最终融合图像与源图像间的交互信息，IM数值越大，表征融合图像中涉及到源图像的原始信息越丰富.fS可以在一定程度上反映融合图像中各像素点的活跃程度，fS数值越大，代表融合图像包含的显著信息越丰富.QWF反映了最终融合图像相对原始图像的信息保留程度，QWF的数值与信息保留程度成正比.图6和图7给出了2组待融合源图像的融合效果.

图6　多聚焦图像融合结果

图7　多波段遥感图像融合结果

实验结果表明，基于方法1的融合图像在直观效果上显得“较黑”，且没有能够对源图像中的细节信息进行充分描述，整体效果较差；方法2和方法3生成的最终融合效果图像虽然在整体亮度水平上较为理想，但在细节信息表达能力上表现不佳，甚至不如方法1的效果.例如，在图6中的右上方标识“ES Maginifier Quality”的描述上，方法2和方法3的仿真效果较为模糊，相对而言，方法1的细节信息较为清晰，但远远不及文中方法得出的结果；在图7右下方的白色建筑物描述上，方法1的结果较方法2和方法3显得更有层次感，而文中方法的表现则更令人满意.

表1以EI,IM,fS,QWF4种客观评价指标为例，给出了两组仿真实验中4种对比方法的比较结果.结果表明，文中方法较其他3种融合方法拥有更理想的客观指标结果，无论在信息量、交互信息量、空间频率还是加权融合质量指数指标上均具有显著优势.因此，客观指标数据与直观评价结果是大致吻合的.

表1　4种融合方法的客观指标值比较

5结束语

文中将IF理论模型与PCNN相结合构成一种新型模型，并综合Shearlet变换理论的优势，提出一种新型的图像融合方法，针对经典PCNN模型的缺陷进行了改进，提出了IF-PCNN理论模型，并将其作为高、低频微观子带图像的融合方法.仿真实验验证了文中方法的有效性.

参考文献:

[1]马东辉,薛群,柴奇,等.基于图像信息的红外与可见光图像融合方法研究[J].红外与激光工程,2011,40(6):1168.

[2]刘斌,彭嘉雄.基于非下采样三通道不可分对称小波的多光谱图像融合[J].电子学报,2011,39(5):1094.

[3]陈浩，王延杰.基于小波变换的图像融合技术研究[J].微电子学与计算机，2010,27(5):39.

[4]赵子沂,郑永果.基于脊波的多光谱和全色图像融合方法研究[J].计算机工程与应用,2012,48(15):164.

[5]王斐,梁晓庚,崔彦凯,等.非负矩阵分解和新轮廓波变换的图像融合方法[J].计算机工程与应用,2013,49(5):150.

[6]莫建文,马爱红,首照宇,等.基于Brenner函数与新轮廓波变换的多聚焦融合算法[J].计算机应用,2012,32(12):3353.

[7]王雷,李彬,田联房.基于平移不变剪切波变换的医学图像融合[J].华南理工大学学报(自然科学版),2011,39(12):13.

[8]LIU X,ZHOU Y,WANG J J.Image fusion based on shearlet transform and regional features[J].InternationalJournalofElectronicsandCommunications,2014,68(6):471.

[9]SHI C,MIAO Q G,XU P F.A novel algorithm of remote sensing image fusion based on Shearlets and PCNN[J].Neurocomputing,2013,117(6):47.

[10]ECKHORN R.Neural mechanisms of scene segmentation:recordings from the visual cortex suggest basic circuits or linking field models[J].IEEETransactionsonNeuralNetwork,1999,10(3):464.

[11]El-TAWEEL G S,HELMY A K.Image fusion scheme based on modified dual pulse coupled neural network[J].IETImageProcessing,2013,7(5):407.

[12]ZHUANG H L,LOW K S,YAU W Y.Multichannel pulse-coupled-neural-network-based color image segmentation for object detection[J].IEEETransactionsonIndustrialElectronics,2012,59(8):3299.

[13]CHEN Y L,PARK S K,MA Y D,et al.A new antomatic parameter setting method of a simplified PCNN for image segmentation[J].IEEETransactionsonNeuralNetworks,2011,22(6):880.

[14]CHOU N,WU J R,BAI B R,et al.Robust automatic rodent brain extraction using 3-D pulse-coupled neural networks[J].IEEETransactionsonImageProcessing,2011,20(9):2554.

[15]ZHONG Y F,LIU W F,ZHAO J,et al.Change detection based on pulse-coupled neural networks and the NMI feature for high spatial resolution remote sensing imagery[J].IEEEGeoscienceandRemoteSensingLetters,2015,12(3):537.

[16]ATANASSOV K.Intuitionistic fuzzy sets[J].FuzzySetsandSystems,1986,20(1):87.

[17]GUO K,LABATE D.Optimally sparse multidimensional representation using shearlets[J].SIAMJournalofMathematicalAnalysis,2008,39(1):298.

[18]ZHENG Y,ESSOCK E A,HANSEN B C,et al.A new metric based on extended spatial frequency and its application to DWT based fusion algorithms[J].InformationFusion,2007,8(2):177.

[19]WANG Z B,MA Y D.Medical image fusion usingm-PCNN[J].InformationFusion,2008,9(2):176.

[20]MIAO Q G,SHI C,XU P F,et al.A novel algorithm of image fusion using shearlets[J].OpticsCommunication,2011,284(6):1540.

[21]BURT P,ADELSON E.The Laplacian pyramid as a compact image code[J].IEEETransactionsonCommunications,1983,31(4):532.

[22]LIU Z,BLASCH E,XUE Z Y,et al.Fusion algorithms for context enhancement in night vision:a comparative study[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2012,34(1):94.

[23]苗启广.多传感器图像融合方法研究[D].西安：西安电子科技大学,2005.

(责任编辑惠松骐)