PCA与小波变换的ECT图像融合方法

王莉莉　沈月　陈德运　于晓洋　刘洪波

摘要：电容层析成像技术存在“软场”效应和病态问题，由于这一特性，ECT重建图像的精度受到了影响，在分析电容层析成像基本原理和成像算法的基础上，提出了一种基于PCA变换与小波变换相结合的ECT图像融合方法，首先对待融合的图像进行主分量变换以得到各主分量，然后采用基于特征的小波变换融合方法将待融合图像的信息与第一主分量进行融合，再将此时融合后的信息与其他主分量进行逆变换，得到最终的融合图像，通过仿真实验得到结果表明，融合图像的质量得到了提高，与源图像更加接近，为ECT图像重建的研究提供了一个新的方法，

关键词：电容层析成像；图像重建；PCA；小波变换；图像融合

DoI：10.15938/j.jhust.2016.04.006

中图分类号：TP391.9

文献标志码：A

文章编号：1007-2683（2016）03-0030-06

0引言

电容层析成像技术是最早发展起来的一种过程成像技术，其测量方式具有非侵入性、价格相对低廉、结构比较简单、安全性好、并且易于实现…，正是由于具有这些特点，使得电容层析成像技术在解决多相流检测上具备极大的发展潜能及广阔的应用前景，电容层析成像技术涉及多方面问题，而其中一个关键问题即图像重建，电容层析成像系统重建图像的质量会受到ECT系统非线性和“软场”效应等性质的影响，因此，对于电容层析成像技术来说，探究良好的图像重建算法是一个很重要的问题，

目前，比较常用的图像重建算法主要有线性反投影（LBP）算法、奇异值分解（sVD）法、Tikhonov正则化法、Landweber迭代法及共轭梯度法（CG）等，在ECT领域里最早采用的一种算法即LBP算法，该算法因其简单、计算量小、速度快等优点而被广泛应用，但其重建图像的精度往往不是很高，Tikhonov正则化法在处理病态逆问题上具有很好的成效，LBP及Tikhonov正则化法均为非迭代类的算法，成像速度快，但所成图像往往没有很好的质量然而对于传统迭代类图像重建算法，其所成图像的质量相对较好，Landweber迭代法来源于最速下降法，主要依据为最小二乘准则，目前对于ECT领域来说，是一种较普遍的方法，但其不足之处即收敛速度较慢，对于简单流型来说，共轭梯度法具有成像时间短、收敛速度快的特点，但是在处理复杂流型上效果并不是很好，

各种成像算法各有优缺点，运用不同的重建算法，重建出的图像也存在差异，原因是不同算法对不同的流型敏感度存在着差别，将图像融合技术应用到ECT系统中来融合不同算法生成的图像，以得到成像精度更高的图像，

1.ECT系统的构成及成像原理

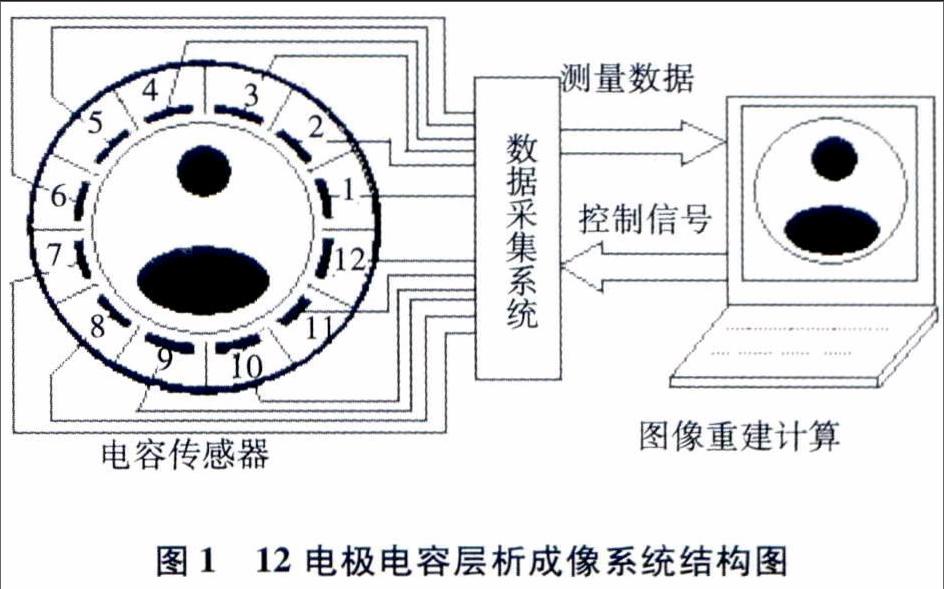
由于多相介质的介电常数通常不同，电容层析成像技术便是依据此原理通过电容传感器获得相对介电常数的分布来进行图像重建的典型的12电极ECT系统结构如图1所示，ECT系统由三部分组成，分别为电容传感器阵列、测量数据采集装置及成像计算机，电容传感器阵列的作用就是为ECT系统提供被测物场分布情况的投影信息；所信息由测量及数据采集装置进行收集，并经过滤波、变换、放大等处理，最终通过接口将数据传给计算机来进行图像重建及显示，

电容层析成像系统的正问题是指在传感器结构尺寸和管道内两相流相分布已知的情况下，通过计算机来求解出各电极对间的电容值，本文以12电极ECT系统为例，各极板依次被选作激励电极，施加固定电压u，其余极板为检测电极，检测出所有极板对之间的电容值，对于12电极的系统，总共需要测量的独立电极对电容值数量由公式N（N-1）/2可得为66个，

式中：C表示两个电容极板间的电容测量值；y为两电极板间的电位差；T为电极的表面闭区间；ε（x，y）为管内介质的相对介电常数分布；Φ（x，y）为电场分布。

图像重建即电容层析成像的逆问题，对于ECT系统最主要的就是完成图像重建工作，通过重建图像可以获得过程参数在二维断面空间的分布情况，从而人们对过程信息的获取和分析能力得到了大大的提高，因此，较传统的局部空间单点测量方式有很大的优势。

由式（1）可知，极间电容与相对介电常数分布存在非线性关系，可表示为：量；m为可测得的独立电容数目；n为成像区域内像素个数，因电容C受物质分布G变化的影响，并由s反映出来，故称为敏感场，ECT系统的逆问题就是由已知的电容c从而反算出介电分布G

2.PCA（主成份分析）

PCA变换也被称为K-L变换、主分量变换或特征向量变换，PCA变换是基于图像统计的特性的变换，能够充分去除相关性，提取集中有用信息到数量尽可能少的主分量中，提高工作效率，已成功应用于遥感图像融合。

当采用PCA融合方法来对待融合图像进行融合时，首先需要做的是，对其中待融合的多光谱图像进行主分量变换以得到各主分量，并确定第一主分量；然后将另一待融合的高分辨率图像与上步得到的第一主分量作直方图匹配，从而得到另一高分辨率图像，用此时得到的高分辨率图像来替代多光谱图像的第一主分量，最后与其他主分量一起作逆主分量变换，从而得到融合图像，

3.小波变换图像融合方法

小波分析是信号多分辨率分析工具，它在信号的时域和频域都有着良好的特性，小波变换融合的基本思想为：首先对已配准的多源图像进行小波分解，小波分解出各个源图像的高频和低频系数，然后对分解后的小波系数矩阵进行融合处理，此时采用区域特征的方法，最后采用小波逆变换得到融合图像，进行小波变换后，图像的数据总量不会增大，这是因为小波变换是非冗余的，并且具有方向性，因此，小波变换在图像融合领域得到了广泛的应用，

4.基于PCA与小波变换的图像融合

基于PCA变换与小波变换相结合的图像融合的基本思想是：低分辨率的图像首先进行主分量变换以得到各个主分量，并同时求得第一主分量，将其设为P₁，对高分辨率图像进行拉伸，使其均值和方差与第一主分量P。相同，然后用基于特征的小波变换融合方法对P₁与高分辨率图像进行融合，新的融合图像包含了高分辨率图像的信息，设为P然后将P₁与其他主分量一起作逆主分量变换就得到最终的融合图像。

5.实验结果

实验选取线性反投影（LBP）和共轭梯度重建算法针对不同流型进行图像重建，对不同重建算法下生成的同一流型图像进行融合，融合时分别采用PCA变换、小波变换及本文所提出的基于PCA变换与小波变换相结合的融合方法，在Matlab软件下进行仿真实验，实验结果如表l所示。

现采用图像信息熵、平均梯度及均方根误差三种客观性评价指标对融合后图像的质量进行分析比较。

分析表2、表3、表4，首先分析图像信息熵，从表中我们可以看出，采用本文提出的融合方法融合后图像的信息熵的值大于PCA融合方法及小波融合方法融合后图像信息熵的值，表明采用本文提出的融合方法的融合效果更好，同理分析比较平均梯度及均方根误差两种评价指标均可得出此结论，平均梯度越大融合效果越好，均方根误差越小融合效果越好，

6.结论

本文提出了一种基于PCA变换与小波变换的ECT图像融合方法，该方法有机的将PCA变换与小波变换相结合，实验选取线性反投影（LBP）和共轭梯度算法分别对层状流、核心流、环状流模型进行图像重建，对不同重建算法下生成的同一流型图像进行融合，根据以上评价指标的实验结果表明，用本文提出的方法融合出的图像质量要优于典型的PCA及小波融合方法，为ECT图像重建的研究提供了一个新的方法。