一种求解KdV-Burgers方程的迎风超紧致差分格式

E-mail:sunja@nwnu.edu.cn

一种求解KdV-Burgers方程的迎风超紧致差分格式

孙建安，郭小霞,贾伟

(西北师范大学物理与电子工程学院,甘肃兰州730070)

摘要：提出了一种迎风超紧致差分格式(USCD)，利用Fourier分析方法对该格式的数值特性进行了分析，并与其他的迎风差分格式和迎风紧致差分格式做了对比.结果反映出USCD具有更好的分辨率和更低的耗散.通过对Burgers方程和KdV-Burgers方程的数值模分析，进一步证实了USCD格式有更高的精度和对长时间演化问题的有效性.

关键词：迎风超紧致差分格式(USCD)；KdV-Burgers方程；数值解

收稿日期：2015-01-15;修改稿收到日期:2015-04-20

基金项目:国家自然科学基金资助项目(10875098)

作者简介：孙建安(1964—)，男，甘肃天水人，教授，博士,硕士研究生导师.主要研究方向为计算物理.

中图分类号：O 241.82文献标志码：A

Anupwindsupercompactdifferencescheme

forKdV-Burgersequation

SUNJian-an,GUOXiao-xia,JIAWei

(CollegeofPhysicsandElectronicEngineering,NorthwestNormalUniversity,Lanzhou730070,Gansu,China)

Abstract:In this paper,an upwind super compact difference scheme(USCD)is proposed.The numerical characteristics of USCD are analyzed by using Fourier analysis,and compared with other upwind difference schemes and upwind compact difference schemes.According to analysis,it is found that USCD has better resolution and lower dissipation.Numerical solutions of the Burgers and KdV-Burgers equations show that the USCD scheme has high-order accuracy and is effective for long time evolution.

Keywords:upwindsupercompactdifferencescheme(USCD);KdV-Burgersequation;numericalsolutions

有限差分法是微分方程数值解法中发展最早、理论最完善、应用最广泛的数值计算方法之一.1992年，Lele对一类Padé格式进行了总结，提出了紧致有限差分格式[1]，与传统差分格式相比，紧致格式的内点模板更小，数值精度更高.1993年Fu等在紧致差分格式中引入迎风机制[2].1997年Fu等提出了五格点五阶精度的迎风紧致格式[3]，利用Fourier分析方法对格式稳定性进行了分析，对二维N-S方程和可压缩流体问题进行了数值模拟，其结果反映出迎风紧致格式能够有效抑制非物理振荡，更适合于多尺度复杂流场的计算.

2000年Chu等建立了三格点6阶精度的紧致差分差分格式[4-5]，并对格式的稳定性进行了分析.2008年林东等在其基础上提出了组合型超紧致差分格式[6]，该格式只需三个格点就可以达到任意阶精度，对KdV-Burgers方程和浅水方程的数值模拟反映出了该格式的高精度.但以前的超紧致差分格式还没有看到过引入迎风机制的文献.

本文针对KdV-Burgers方程提出了一种迎风超紧致差分格式，该格式只需三个基架点就可以达到五阶精度，并且具有更好的分辨率和更低的耗散.

1KdV-Burgers方程的迎风超紧致差分格式

1.1KdV-Burgers方程

考虑如下KdV-Burgers方程[6-7]

其中，μ1为耗散系数；μ2为色散系数.

1.2空间离散格式

将迎风机制引入超紧致差分格式，构造如下形式的三格点模板的迎风超紧致差分格式(Upwind Super Compact Difference Scheme，简称USCD)，其精度可以达到五阶.对于内节点，具体格式为

其中α1,β1,γ1,δ1,a1,b1,c1,α2,β2,γ2,δ2,a2,b2,c2分别为差分格式的系数.对上述逼近式分别做泰勒展开可得到系数之间的如下关系式

(4a)

(4b)

据此可求得差分格式系数的值.可以验证，当系数满足(4)式时，格式(2),(3)可以达到5阶精度.

对于左边界节点，本文构造了如下形式的差分格式

这里可同样使用泰勒展开得到系数a11,a12,b1,a21,a22,b2之间的如下关系式

(7a)

(7b)

同样可以验证，当系数满足(7)式时，格式(5),(6)可以达到三阶精度.

由此，本文构造的整个区间[a,b]上的迎风超紧致差分格式为

内点五阶精度的迎风超紧致格式为

左边界三阶精度的组合紧致格式为

右边界三阶精度的组合紧致格式为

联立内点和边界点格式，可以得到如下形式的系数矩阵A:

记向量F和B分别为

求解代数方程组

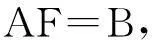
即可得到各节点的一、二阶导数值.

1.3格式分辨率分析及耗散波数

分辨率分析可以了解一个格式对不同尺度的物理量的分辨能力[8].因此对于一阶导数的差分，采用Fourier分析方法计算出修正波数kh，并考察其与精确波数k′h的逼近程度，依此分析格式的分辨率及耗散误差.

图1和图2给出了一阶显式迎风格式(UD1)，三阶迎风紧致格式(UCD3)[9]，五阶迎风紧致格式(UCD5)[8]，五阶迎风超紧致格式(USCD,即本文格式)分辨率和耗散波数的比较，以判断格式的分辨率和耗散情况.

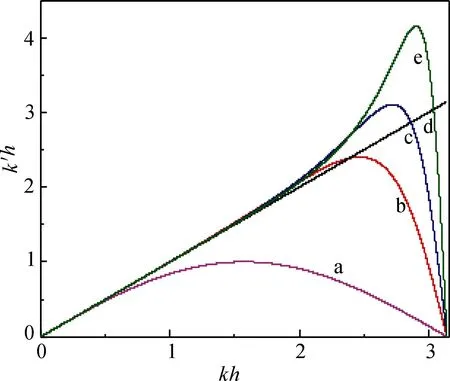
图1　 不同格式一阶导数修正波数虚部(色散误差)

图2　 不同格式一阶导数修正波数实部(色散误差)

从图1可以看出，本文所构造的USCD格式(d线)色散误差与准确波数(e线)符合最大，相比于传统一阶迎风格式(a线)、三格点紧致迎风格式(b线)和五格点紧致迎风格式(c线)，五阶迎风超紧致格式(USCD)具有更高的分辨率.

从图2可以看出，本文所构造的USCD格式(d线)耗散误差与准确波数(e线)符合最大.由图2可见，当kh=2.5时，本文所构造的USCD格式(d线)更接近于准确波数，从而反映出USCD格式相比于传统一阶迎风格式(a线)、三格点紧致迎风格式(b线)和五格点紧致迎风格式(c线)，五阶迎风超紧致格式(USCD)具有更低的耗散.

更值得注意的是，本文构造的五阶迎风超紧致格式在最大的波段范围内，相比较三格点三阶紧致迎风格式(UCD3)，三格点五阶迎风超紧致格式(USCD)比三格点三阶迎风紧致格式(UCD3)具有更好的分辨率和更低的耗散，甚至在一些波段内USCD的分辨率高于UCD5，其耗散误差也低于UCD5.

1.4时间离散格式

时间离散采用四阶修正Runge-Kutta方法[9]，若设方程为

式中G为对空间变量的微分算子，则四阶修正Runge-Kutta格式为

2数值算例

2.1Burgers方程

若方程(1)中μ2=0，则方程(1)可变为Burgers方程.因此考虑如下Burgers方程的初边值问题[10]

式中μ1为耗散系数.上述方程当初值为

时的精确解为[11]

其中

为方便比对数值结果的误差，引入误差范数L2与L∞，其定义分别为[12]

采用本文构造的五阶精度的迎风超紧致格式(USCD)进行计算，取h=0.02,节点数N=51，Δt=0.001.表1给出了五阶精度的迎风超紧致格式(USCD)、三阶精度的迎风紧致格式(UCD3)和五阶精度迎风紧致格式(UCD5)在不同ε时的数值解误差比较.可以看出,USCD的精度明显高于UCD3，甚至比UCD5精度略高，显然其数值解达到了五阶精度.

2.2KdV-Burgers方程

对于方程(1),当初值为

其精确解为[13]

采用本文提出的五阶USCD格式进行计算，取a=-20,b=20,h=1，节点数N=41,Δt=0.001.对于三阶导数值，采用将一阶导数值作为函数值代入(16)式再进行一次求解即可得到.表2给出了不同格式数值结果的误差比较.可以看出USCD的精度比UCD3更高，在长时间演化过程中USCD的精度略高于UCD5.

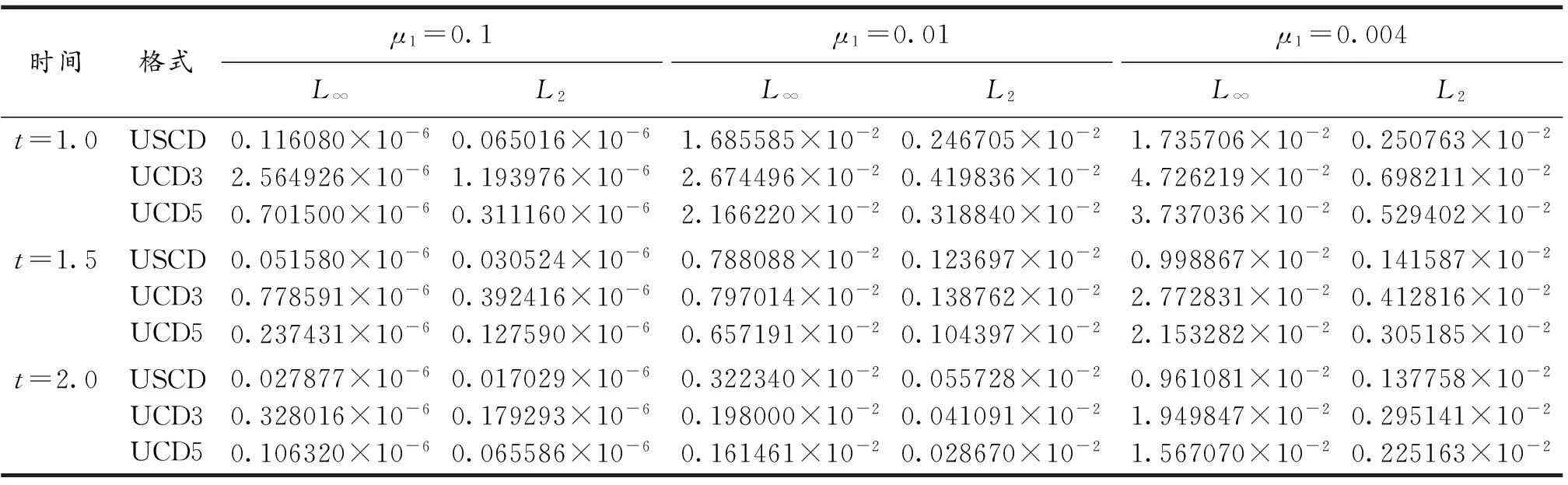
表1　 Burgers方程不同格式误差范数的比较

表2　KdV-Burgers方程不同格式误差范数的比较( a=-20, b=20, μ1=0.3,μ2=0.1)

图3给出了KDV-Burgers方程在不同时刻的解.可以看出，当μ1=0.3,μ2=0.1时，KdV-Burgers方程在不同时刻解的波形能够保持完整准确.即使在t=50的时刻点，USCD格式也能够高精度的进行数值模拟，从而也体现了USCD格式对长时间演化问题的有效性.

( μ1=0.3,μ2=0.1)

3结束语

本文提出的迎风超紧致差分格式(USCD)从理论分析和数值结果两方面表明了其数值模拟的优良性能.只需三个格点就可以达到五阶精度，并且具有较高的分辨率和较低的耗散.通过两个算例，表明了USCD格式具有高精度以及对长时间演化问题的有效性.

参考文献:

[1]LELE S K,Compact finite difference schemes with spectral-like resolution[J].JComputPhys,1992,103:16.

[2]FU D X,MA Y W,LIU H.Upwind compact schemes and aplications[C]//Proceedingsof5thInternationalSymposiumonCFD.Sendai:Japan Society of Computational Fluid Dynamics,1993:104.

[3]FU D X,MA Y W.A high order accuracy difference scheme for complex flow fields [J].JComputPhys,1997,134:1.

[4]CHU P C,FAN C W.A three-point combined compact difference scheme[J].JComputPhys,1998,140(2):370.

[5]CHU P C,FAN C W.A three-point sixth-order staggered combined compact difference scheme[J].Mathematicalcomputermodeling,2000,32:323.

[6]林东,詹杰民.浅水方程组合型超紧致差分格式[J].计算力学学报,2008,25(6):1.

[7]刘万海.(1+1)维非线性演化方程的B样条Galerkin有限元数值解[D].兰州：西北师范大学,2009.

[8]KIM J W,LEE D J.Optimized compact finite difference schemes with maximum resolution[J].AIAAJournal,1996,34(5):887.

[9]沈露予.不可压缩Navier-Stokes方程高精度算法研究[D].南京：南京信息工程大学,2012.

[10]孙建安,陈继宇,刘万海,等.用调和微分求积法数值求解Burgers方程[J].西北师范大学学报(自然科学版),2009,45(5):34.

[11]COLE J D.On a quasi-linear parabolic equation occurring in aerodynamics[J].ApplMathComput,2005,170:859.

[12]DOGAN A.Numerical solution of RLW equation using linear finite elements within Galerkin’s method[J].AppliedMathematicalModelling,2002,26:771.

[13]LIU S S,LIU S D.NonlinearEquationsinPhysics[M].Beijing:Peking University Press,1997.

(责任编辑孙对兄)