对我国房地产泡沫测度方法研究

对我国房地产泡沫测度方法研究

张舒涵

(安徽财经大学 金融学院, 安徽 蚌埠 233030)

摘要：首先明确房地产泡沫的概念，之后在比较已有的指标体系、统计检验和基础价值这三类房地产泡沫的测度方法的基础上，选择了改进后的状态空间模型，收集2000年至2012年的年度数据，通过分别建立房地产需求、房地产供给以及房地产基础价值的状态空间模型，运用卡尔曼滤波、描述性分析、ADF平稳性检验和协整检验对我国房地产市场的泡沫度进行分析及测度，最后基于实证研究的结果提出改进后模型测度方法的使用技巧。

关键词：房地产价格；状态空间模型；泡沫度

中图分类号：F293.3

文献标识码：A

文章编号：1671-9743(2015)01-0022-04

Abstract：Firstly,the concept of real estate price buble is clearly put forward.Then based on the comparison of existing measuring methods and data from 2000 to 2012,an improved method is employed in the construction of SSpace modeles of supply,demand and fundamental price to measure the real estate price buble.In addition,Kalman filtering,descriptive analysis,ADF stationary as well as co-integration test are used in the empirical process.Finally,result of empirical study is analyzed and the usage of SSpace models on evaluating real estate price buble is suggested.

收稿日期：2014-10-25

作者简介：张舒涵，1991年生，女，安徽阜阳人，硕士研究生，研究方向：银行经营与管理。

Analysis on Evaluation Methods of China’s Real Estate Price Buble

ZHANG Shu-han

(SchoolofFinance，AnhuiUniversityofFinanceandEconomics,Bengbu,Anhui233030)

Key words：housing price;SSpace model;real estate price buble

一、房地产泡沫的定义及其测度方法

(一)房地产泡沫的定义

房地产市场的供给和需求这两个层面共同决定了房地产的基础价值，当投机等非理性因素作用于房地产价格，使其在市场上的实际价格超出理论上的基础价格时，房地产泡沫现象随之产生。基于此将泡沫定义为：房地产实际价格对基础价格的非平稳偏离的部分。

(二)国内外研究及测度方法

国外早在上世纪80年代就已形成房地产泡沫的系统研究，目前关于泡沫存在性的验证研究、泡沫的测度方法研究、泡沫影响因素及与经济发展的宏观分析等方面均有全面大量的研究成果。野口悠纪雄(1987)提出通过收益还原价格对房地产泡沫进行测度。Wong(1998)通过构建动态模型，展示了热钱大量流入时，房地产商对市场的过度乐观预期以及居民预期之间的相互作用产生的群体行为在房地产泡沫产生和膨胀过程中的作用机制。

自上世纪90年代后期住房制度改革后，国内才开始对房地产泡沫的测度进行研究，目前主要是借鉴国外的理论与方法。如姜春海通过构建房地产竣工造价预测方程，运用统计检验方法分析房地产市场供给弹性[1]。

对比国内外成果发现以下房地产泡沫测度研究的特点。一是主要借助金融资产泡沫研究，利用理性模型法虽能较好解释泡沫现象但缺乏对非理性因素的考虑。二是以三类静态均衡的测度法为主。

1.指标体系测度法

此方法通过选取房价——收入比、租售比、房屋空置率等指标或者从金融、消费、房屋供给等层面选取一系列指标体系通过加权平均对房地产泡沫进行测度。尤明利用指数合成法，首先为相单位各异、不能直接相加的各单个指标确定临界值，然后将各单个指标与其临界值相比得指数的抽象值，最后根据各指数在整个体系中的重要程度赋权计算综合指数[2]。

2.统计检验测度法

此方法从计量经济学原理入手，将房地产市场存在泡沫作为原假设，通过对房地产实际价格进行统计检验，判断是否拒绝原假设来测度泡沫是否存在。由于统计检验所需样本数据较大且要求市场有效，因此用于测度房地产泡沫具有局限性。

3.基础价值测度法

此方法从泡沫形成的原理入手，通过构建模型估算出供求关系作用下相对静止的基础价值，并与实际价格相比较实现对泡沫的测度。基础价值的确定一是根据房产收益贴现计算基础价值；二是根据房地产市场供求关系计算基础价值，如McCarthy通过构建结构性房地产部门，加入误差修正项测算美国房地产市场供求均衡时的价格作为基础价值[3]。

以上三类国际通用测度法各有弊端，指标法从某几个指标入手，往往指标单一，不够全面；统计法需要大量的统计资料，而中国各城市的房地产统计数据不够完善，统计检测的基础比较薄弱；基础价值测度法不适合还未稳定的中国房地产市场。因此目前就选用统一方法测度难以达成共识。

通过改进以往的研究方法，本文不仅分别考虑了需求与供给模型，还将供求关系联立到一个模型中，将由供求关系动态决定的不可观测的房地产基础价格作为一种相对稳定变量，通过构建状态空间模型加以估计，从而测度泡沫。选用状态空间主要有以下优点：首先，状态空间模型可将不可观测的状态变量纳入可观测变量进行估计；其次，可以分析状态随时间变化的规律及验证所选状态是否反映观测变量的真实情况；再次，状态空间模型所运用的卡尔曼滤波是基于所有可得信息估计状态向量的最理想的递推算法[4]。

二、模型设计

(一)变量选取与数据说明

房地产基础价格受供求关系决定及诸多宏微观因素影响。影响房地产供给的因素主要包括，房地产销售价格、宏观经济增长、货币供应量、开发商可贷资金量及使用成本，影响房地产需求的因素主要包括，房地产销售价格、居民可支配收入、一般商品价格。考虑到我国房地产市场以商品房交易为主且是社会热点具有重要的现实意义，因此以商品房为研究对象，选取8个变量反映房地产供需情况，具体描述见表1。分别用商品房竣工面积CA和施工面积SA作为房地产供给和需求的代理变量，RI、GDP、ML和CHP为影响房地产供给的变量，UPDI、RPI、RI和CHP为影响房地产需求的变量。值得一提的是本文选取的是商品零售价格指数RPI而非消费价格指数反映一般商品价格，以更准确地反映资本市场上价格对商品房需求的影响。

表1中的变量选取自2000至2012年的年度数据，数据来源国家统计局。RI用名义利率去除通货膨胀率得出，对GDP、ML、UPDI用价格指数平减消除价格因素影响，通过对价格调整后的时间序列观察，未呈现明显季节规律，无需进行季节调整。对除实际贷款利率RI外的其他变量取对数以消除异方差，且对数形式代表变量的弹性便于比较与判断。

表1　变量描述

(二)模型建立

1.商品房需求的状态空间模型

信号方程：

lnSA=sv1t×lnCHPt+sv2t×lnUPDIt+sv3t×RIt+sv4t×lnRPIt+λt

状态方程：

sv1t=sv1t-1+ε1;sv2t=c(1)+sv2t-1+ε2；

sv3t=c(2)+sv3t-1+ε3;sv4t=sv4t-1+ε4；

残差λt、ε1、ε2、ε3、ε4假定独立同分布，方程为常数定值且互不相关。未知参数c(1)、c(2)的初始值通过建立普通回归方程得出，用常数项作为c(1)的初始值，取log(残差平方和/数据的个数)作为c(2)的初始值。

2.商品房供给的状态空间模型

信号方程：

lnCAt=cv1t×lnCHPt+cv2t×RIt+cv3t×lnMLt+cv4t×lnGDPt+γt

状态方程：

cv1t=cv1t-1+μ1;cv2t=c(3)+cv2t-1+μ2；

cv3t=cv3t-1+μ3;cv4t=cv4t-1+μ4；

残差γt、μ1、μ2、μ3、μ4假定独立同分布，方程为常数定值且互不相关。

3.商品房基本价值的状态空间模型

联立商品房需求及供给的信号方程，将实际的商品房平均销售价格CHP替换为基本价值的变量FP，作为基本价值的状态空间的信号方程。运用卡尔曼滤波分别估计商品房需求及供给的状态空间的变参数模型，得到残差参变量ε1、ε2、ε3、ε，μ1、μ2、μ3、μ4的估计值，并作为已知变量带入信号方程：

lnSAt=sv1t×lnCHPt+sv2t×lnUPDIt+sv3t×RIt+sv4t×lnRPIt+λt

lnCAt=cv1t×lnCHPt+cv2t×RIt+cv3t×lnMLt+cv4t×lnGDPt+γt

状态方程：

lnFPt=lnFPt-1

4.泡沫度的计算

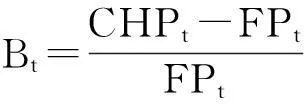
三、实证检验及结果

(一)描述性分析

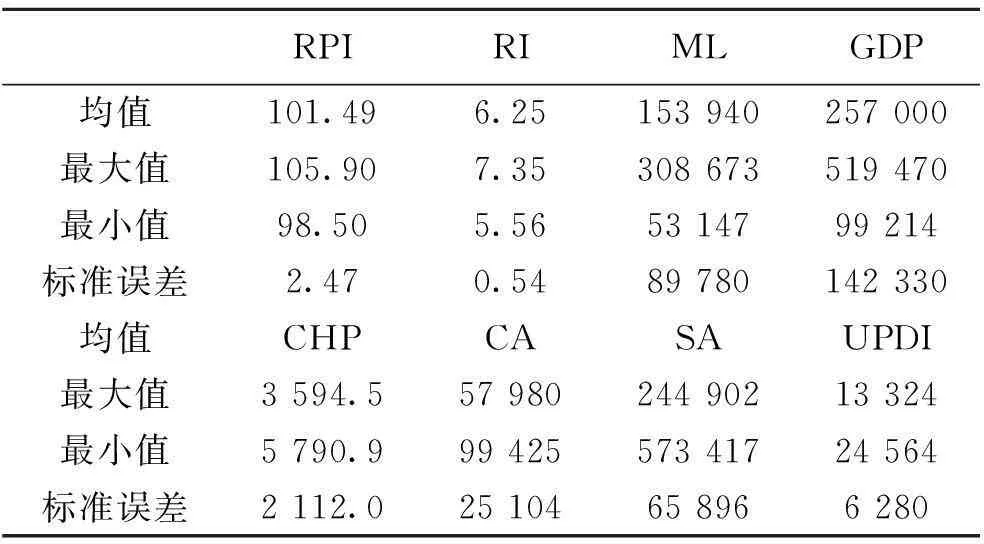
表2　描述性统计

从表2可以看出，2000年至2012年商品房平均施工面积远大于平均竣工面积，约为其4倍；期间GDP、ML、UPDI均稳步增长，实际贷款利率较低，均值仅为6.25%，标准误差为0.54；商品房平均销售价格在样本期间由2 112.0元/平方米增至5 790.9元/平方米，增加了1.74倍。

(二)平稳性检验

由于状态空间模型要求变量平稳或非平稳但存在协整关系，为了保证不存在伪回归的这一实证检验前提，首先对各时间序列变量进行ADF检验。根据图1选择包含截距和趋势项，根据赤池信息准则选取滞后阶数，发现所有变量都是非平稳的，经过一阶差分后在5%的显著性水平下增长率都是平稳的，可以认为所有变量都是I(1)过程[5]。

(三)协整性检验

对一阶差分平稳的各对数时间序列变量进行协整检验，验证变量间是否具有长期均衡关系，能否建立状态空间模型。由于样本容量有限，通常采用的Johansen协整检验效果不好，因此本文对商品房需求模型和供给模型中的信号方程分别进行OLS回归，对所得残差序列λt和γt分别进行平稳性检验从而间接检验变量间的协整性。结果见表3，λt和γt在5%的显著性水平上均通过了ADF检验和PP检验，说明商品房需求模型和供给模型中各变量间分别存在协整关系。

表3　残差序列平稳性检验结果

(四)对泡沫度的测算

根据建立的全国房地产状态空间模型计算房地产基础价值，并在已知平均销售价格的基础上计算出其具体数值，结果见表4。

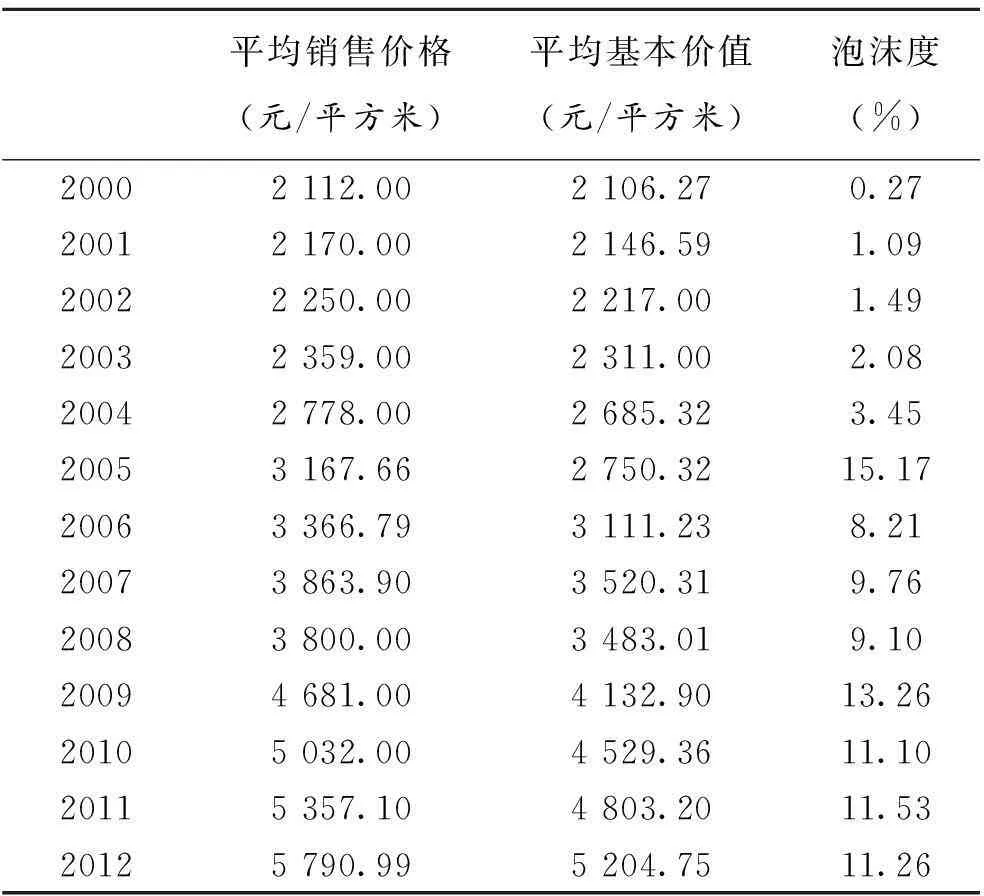
表4　房地产泡沫度测算结果

在样本期内，泡沫度平均值为7.52%，2000到2004年房地产价格缓慢增长，平均泡沫度仅为1.68%；2005年，泡沫度猛然增高，达到峰值15.17%；之后3年泡沫度回落到9%左右直到2009年爆发全球金融危机迎来第二个小高峰，2010至2012年泡沫度小幅回落，平均泡沫度为11.3%。

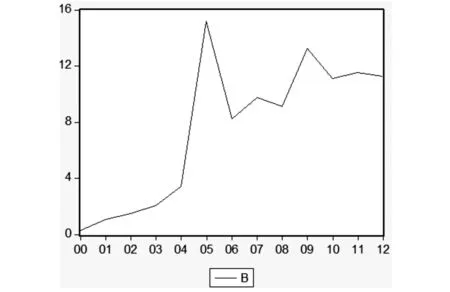
图1　泡沫度走势

非理性投机因子对价格的偏移影响可能是暂时的，之后价格会回归到理性水平；也可能是持久的，价格会不断偏离理性水平，价格偏差越积越大形成泡沫，最终带来房地产市场的崩盘。为了判断价格偏移的性质对泡沫度进行平稳检验，结果显示，泡沫度序列经过一阶差分后才平稳，表明原序列是不遵循随机游走规律的非平稳过程，我国房地产存在泡沫。

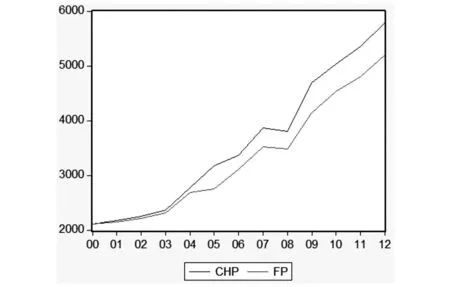
图2　房地产销售价格CHP和基础价值FP走势

四、测度方法的使用和技巧

(一)方法使用的主要事项

1.样本容量

当样本容量足够大时，通常采用Johansen协整检验法验证变量间是否存在长期协整关系，从而建立状态空间模型。当样本容量较小，如测度我国房地产泡沫程度时，由于我国自上世纪90年代后期才开始进行住房制度改革，可获得有关商品房为代表的房地产的各种价格样本量有限，难以满足Johansen协整检验的要求。此时可以选择对需求模型和供给模型中的信号方程分别进行OLS回归，对所得的两个残差序列分别进行平稳性检验从而间接检验变量间的协整性。

2.参数估计时对状态空间模型的选择

利用最大似然法估计状态空间模型的系数，关键是构造一个以观测数据及系统参数为自变量的似然函数L(X,Y|θ)，但有时该函数与参数关系过于复杂，不易优化。对极大似然参数估计进行迭代得出EM算法，在处理不完全数据时极为有效且数值稳定、全局收敛。EM算法由求极值和期望组成，前者是基本的数据处理，后者有时无法用公式表达，此时应采用MCEM算法改写期望的求值并通过极大化近似计算期望，该法能有效消除EM收敛缓慢的问题。

(二)方法使用领域的扩展

除了对实体资产价格泡沫的测度如本文中对房地产市场泡沫的测度，及社会零售品销售总额的分析改进后的状态空间模型还可以应用于金融资产价格的泡沫测度，此类时间序列数据无论在可获性及频率上都很适合模型条件。此外，除了基本的价格分析外，改进后的状态空间模型还可以应用于价格预测。

参考文献：

[1]姜春海.中国房地产市场投机泡沫实证分析[J].管理世界,2005(12):78-81.

[2]尤明.基于指数合成法的北京市房地产泡沫实证研究[J].特区经济,2011(5):62.

[3]McCarthy.Are home prices the next bubble[J].Economic Policy Review,2004:2.

[4]易丹辉.数据分析与EViews应用[M].北京：中国人民大学出版社,2008:278.

[5]赵晓菊.金融计量学[M].上海：上海财经大学出版社,2010:130-133.