基于ALE方法的盾构对接施工钢环顶伸数值模拟及稳定性分析

基于ALE方法的盾构对接施工钢环顶伸数值模拟及稳定性分析

王欢欢1,2,杨丽丽3,杨勋1,2,金先龙1,2

(1.上海交通大学机械系统与振动国家重点实验室，上海200240；2. 上海交通大学机械与动力工程学院，上海200240; 3. 上海应用技术学院，上海201400)

摘要：基于任意拉格朗日-欧拉有限元方法(ALE)，建立了盾构对接施工钢环顶伸的三维数值模型，解决了土体变形流动导致网格畸变的问题，实现了钢环-土体动态耦合过程。分析了钢环顶伸过程中，钢环前侧阻力变化、钢环应力应变状况。研究了不同的顶伸速度下，对钢环顶伸的影响。在充分考虑接触及重力条件下，分析了钢环轴向及侧向的稳定性状况。研究结果可为盾构对接施工方案设计提供参考依据。

关键词：任意拉格朗日-欧拉方法；盾构对接；钢环顶伸；稳定性

中图分类号:U455.4; TP391.9

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.014

Abstract:Based on arbitrary Lagrangian-Eulerian(ALE) method, a three-dimensional finite element model for steel tube extension in shield machine butting was established. The problem of mesh deformation distortion caused by soil flow deformation was solved, the steel tube-soil dynamic coupled process was realized. Resistance change and stress-strain conditions of steel tube during the extension was analyzed. Simulation of steel tube extending under different velocities was implemented. Axial stability and lateral stability of steel tube were analyzed considering contact and gravity status. The results provided a reference for the design of shield butting construction.

基金项目：国家自然科学基金重大研究计划(91215302)；国家自然科学基金(51408207，51478366) 国家自然科学基金项目(91216106);国家重大基础研究项目资助

收稿日期：2014-05-05修改稿收到日期：2014-11-19 2014-05-19修改稿收到日期：2014-09-25

Simulation and stability analysis for steel tube extending in shield butting construction based on the ALE method

WANGHuan-huan1,2,YANGLi-li3,YANGXun1,2,JINXian-long1,2(1. State Key Laboratory of Mechanical System and Vibration，Shanghai Jiaotong University., Shanghai 200240, China;2. College of Mechanical Engineering, Shanghai Jiaotong University., Shanghai 200240, China3. Shanghai Institute of Technology, Shanghai 201400, China)

Key words:arbitrary Lagrangian-Eulerian method; shield butting; steel tube extension; stability

近几十年，盾构施工技术在国内外得到了广泛应用。对于一些超长超大直径的大型隧道，单条隧道连续施工会造成周期过长、施工故障概率高等问题。因此，盾构地中对接施工成为解决该问题的一种有效技术方法[1-2]。盾构地中对接法即两台盾构机从两侧相向掘进至结合地点，在地中进行对接以完成整条隧道的盾构施工，以其安全性、经济性、省时高效等优点被广泛应用。

盾构地中对接方式主要有土木式对接法和机械式对接法：土木式对接法是通过将对接地点地层作加固处理，达到止水和预防地层失稳的效果后，完成盾构拆卸并进行隧道衬砌；机械式对接法是通过对盾构进行特殊设计，而使两台盾构直接进行对接的方法。在工程策划与施工过程中，应结合工程实际情况，根据土层状况、工期造价、精度要求选择对接方法。相比较机械对接法，土木对接法以其经济性更为常用，也是本文对接施工所采用的方法。

对于直径接近和超过15m的超大直径隧道，盾构对接施工仍是一项具有挑战性的世界级难题，国际上也缺乏足够的经验积累和深入研究。为了确保超大直径盾构对接施工的安全和质量，有必要对对接施工中关键技术问题需要进行深入研究。其中，钢环顶推过程和钢环卸载过程是盾构对接施工中的最关键两步骤。因此，钢环顶推过程和稳定性分析是本项目的研究重点。

钢环在土体中的顶推过程，属于典型的结构-土体耦合问题。对于此类问题，国内外已有一些相关研究。Bauer[3]分析了轮胎在土体上的转动过程，通过将土体的摩擦力及粘滞阻力作为外载荷加载在轮胎上，并没有考虑土体变形等因素的影响；Kushwaha[4]分析了农业机具与土体间的相互作用，并考虑土体的小变形及材料非线性，虽然可以求得机具在土体摩擦力及阻力作用下的动态响应，但是无法模拟土体在农机作用下产生的较大变形，因而会产生较大的偏差；Nezami[5]采用DEM方法模拟了挖掘机铲斗工作的过程，克服了土体大变形带来的网格畸变，并同试验数据进行了比对；Asaf[6]指出利用DEM方法求解结构耦合问题时，其参数的选取缺乏稳定性，导致求解结果失真；Fredj[7]采用ALE方法，模拟了管线铺设的过程，充分考虑管道及土体的大变形问题，有效解决了管道-土体间的耦合作用问题，并利用试验进行了验证。

当薄壁圆筒型构件承受外压时，将在筒壁上产生轴向和环向压力。如果压缩应力超过材料的屈服点或强度极限时，和内压圆筒一样，将发生强度破坏。然而往往在筒壁压应力未达到材料的屈服极限点时，筒体突然失去原有形状发生屈曲失稳。在本项目中，钢环直径较大(15m)，而厚度仅为0.1m，故有可能在未达到材料屈服极限前而发生失稳。对于存在接触面的结构屈曲问题进行分析时，以往研究对于接触区域往往进行单独处理。Herzl[8]采用选代算法首先算出接触区域的虚拟力，然后将这种虚拟力转化成假想弹簧的刚度系数，并对原始刚度矩阵进行修正，以处理屈曲模态中的接触问题。在对钢环进行稳定性分析时，受摩擦力及土体粘滞阻力的影响，如果直接将其简化为虚拟力，将导致计算结果存在一定的偏差。

本文基于ALE方法，提出了盾构对接过程中钢环顶伸的数值模拟方法，研究钢环在顶伸过程中的应力应变状况，进而在充分考虑接触及重力条件下，分析钢环轴向及侧向的稳定性状况，为盾构对接施工提供设计参考依据。

1原理与方法

1.1ALE算法

钢环在顶推过程中，受土体的阻滞作用下，产生一定的位移与变形，同时土体在钢环的作用下发生大变形及塑性流动，需对两者界面间的耦合问题进行有效处理。

为实现对钢环顶推过程和卸载过程的数值模拟，应建立钢环与土体的耦合动力学有限元模型。其中，钢环可以简化为线弹性材料，并且变形较小，但必须考虑土体的弹塑性大变形和塑性流动。为了既能描述钢环的弹性小变形，又能描述土体弹塑性大变形和塑性流动，本项目拟采用ALE (Arbitrary Lagrangian-Eulerian)理论来建立钢环与土体的耦合动力学有限元模型。

ALE方法综合了 Lagrangian 方法与 Euler 方法的优点，在材料域与空间域外引入了参考域，通过在参考域网格上的求解，既解决了Lagrangian 方法中材料的严重扭曲，又可解决 Eulerian 方法中移动边界引起的复杂性问题。

ALE描述中包含三个坐标系：Lagrangian坐标系、Eulerian坐标系以及参考坐标系，三者间的转换关系为：

(1)

式中，Xt表示Lagrangian坐标，i表示参考网格，xt表示Eulerian坐标。vt和ut分别为材料和网格速度，wt为对流速度。

图1为三种坐标系之间的关系示意图。

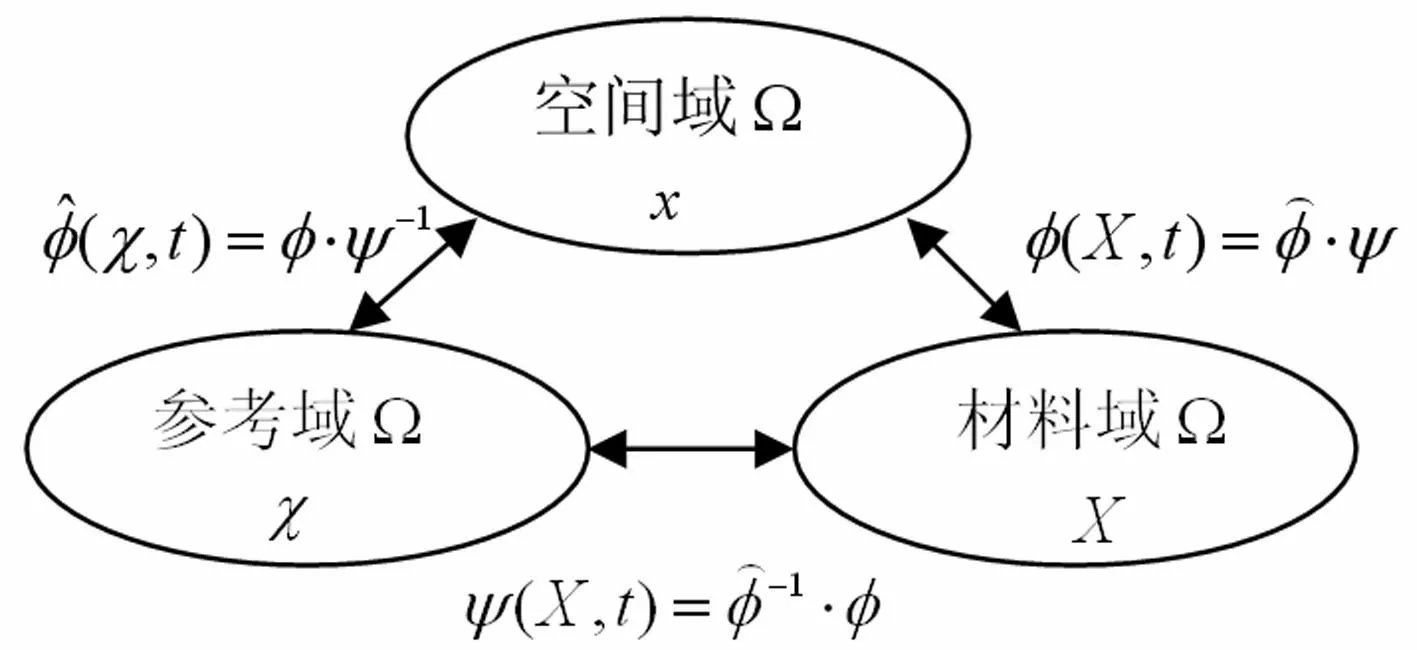
图1　Lagrangian，Eulerian和ALE域之间的映射 Fig.1 Mappings between Lagrangian, Eulerian, ALE descriptions

在不考虑温度变化的情况下，基于ALE描述下的土体连续性方程、动量方程为：

(2)

(3)

基于Lagrangian描述的钢环结构质量方程、动量方程为：

ρs(X,t)J(X,t)=ρ0(X,t)J0(X,t)

(4)

(5)

式中，ρs为钢环密度；J为空间和材料坐标间的Jacobian行列式；u为固体结构位移；X为Lagrangian坐标；bi为体力；σij为应力张量。

钢环与土体间的相互作用通过罚函数耦合方式来定义。罚函数方式耦合通过跟踪流体与结构之间的相对位移来施加节点力，节点力的大小与位移成比例关系。

1.2显式计算方法

采用 ALE 建模理论建立的钢环-土体耦合动力学有限元模型是一个典型的非线性动力学问题。可以采用显式计算方法来对这类复杂非线性动力学问题进行数值求解。

对于某一个时刻，非线性动力学系统的运动方程为：

(6)

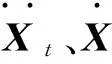
采用显式中心差分法对上式进行数值求解，假定0，t1，t2，…，tn时刻节点位移、速度与加速度均为已知，现求解tn+1(t+Δt)时刻的结构动力响应。在中心差分法中，加速度和速度可以用位移表示，即

(7)

将式(7)代入式(6)中，即可得中心差分法的递推公式

(8)

式中

分别为有效质量矩阵与有效载荷向量。求解式(8)，即可获得t+Δt时刻节点位移向量Xt+Δt。在整个时域范围内，可由上述递推公式求得各个离散时间点处节点的位移、速度和加速度。

显式计算方法由于采用集中质量矩阵，运动方程的求解是非耦合的，不需要组集成总体刚度矩阵，并且采用中心单点积分，因此大大节省存储空间和求解机时。

2工程概况及模型建立

2.1问题概述

盾构机对接位置及周边土体几何简图见图2。该对接方案的具体思路为：首先1号盾构掘进至指定位置，进行隧道加固、泥水仓固化，盾构部分结构拆除，此时2号盾构同时在正常推进，在距离对接位置50m处，进行相对位置探测(多次)，并进行修正掘进(多次)，并到达对接地点。

在到达指定位置后，2号盾构进行隧道加固、刀盘仓内固化、盾构部分结构拆除，准备工作就绪后进行钢环套体顶伸，并达到指定的顶伸长度，见图3。钢环顶伸到位后，进行土体冻结达到一定强度。随后进行冻结施工，清理刀盘内泥土，对接部密封并加固、盾构机解体与清理等一系列工序。在其中钢环顶伸作为较为关键的步骤，将直接关系到盾构对接能否顺利完成，所以需对其顶伸过程中的应力应变状况及稳定性进行深入研究。

图2　盾构机及土体几何简图 Fig.2 Position of shield and soil

图3　钢环顶伸示意图 Fig.3 Diagram of steel tube promote

2.2盾构顶推有限元模型

据提供的工程地质勘探资料，以钢环顶伸区域为核心区域，采用六面体实体单元，建立了土体的分层有限元模型，见图4。

钢环直径为15m，而厚度仅为0.1m，制造加工存在较大的难度。在保证足够的强度下，为降低制造难度，初步设计中钢环前端没有采用刃角构造，在随后的研究中可以考虑不同结构的影响。钢环所在位置的局部视图见图5，钢环顶伸区域的网格进行了细化，对密封圈等结构进行了简化处理。

图4　有限元整体模型 Fig.4 Integrated finite element model

图5　钢环处有限元局部模型 Fig.5 Partial finite element model of steel tube

2.3材料参数与边界条件

目前广为接受的是采用弹塑性材料模型来模拟土体材料的非线性力学行为，通常情况下常采用相对简单的材料模型，使用时其屈服面遵循德鲁克-普拉格(Drucker-Prager)屈服准则或莫尔-库仑(Mohr-Coulomb)屈服准则。本仿真数值模型采用的是软件中提供的Drucker-Prager材料本构，各土层分布及材料参数见图2及表1。

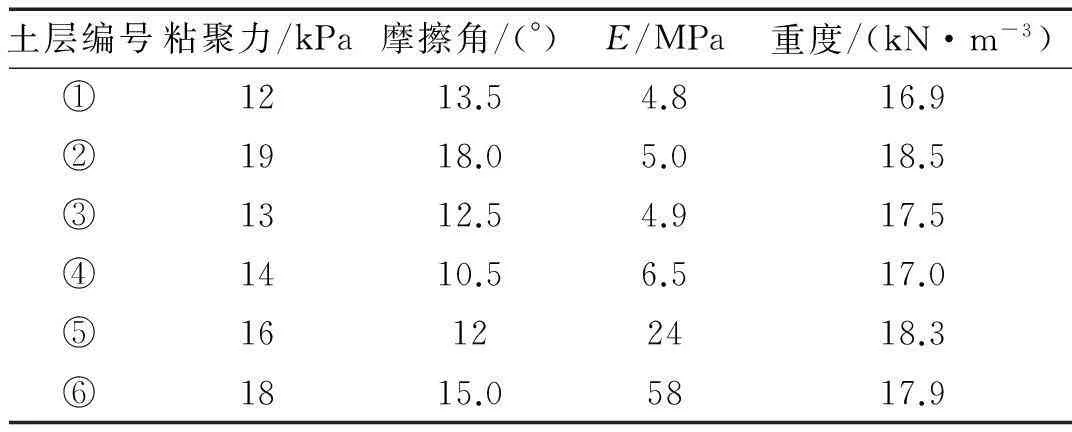
表1　各土层材料参数

在有限元模型中，土体底部为全约束，侧面法向约束，上部为自由端，并整体施加全局重力。

2.4初始地应力平衡

在处理初始地应力时，主要考虑重力场对土体的作用，且暂不考虑盾构与土体间的作用关系。重力初始平衡首先对土体有限元模型加载重力，然后将平衡状态时刻的土体应力场导出，作为初始应力加载。仿真模型采用此种方法可以避免初始有限元模型在重力作用下的大变形，较好的模拟了实际变形情况。土体初始沉降及土体初始应力见图6、图7。

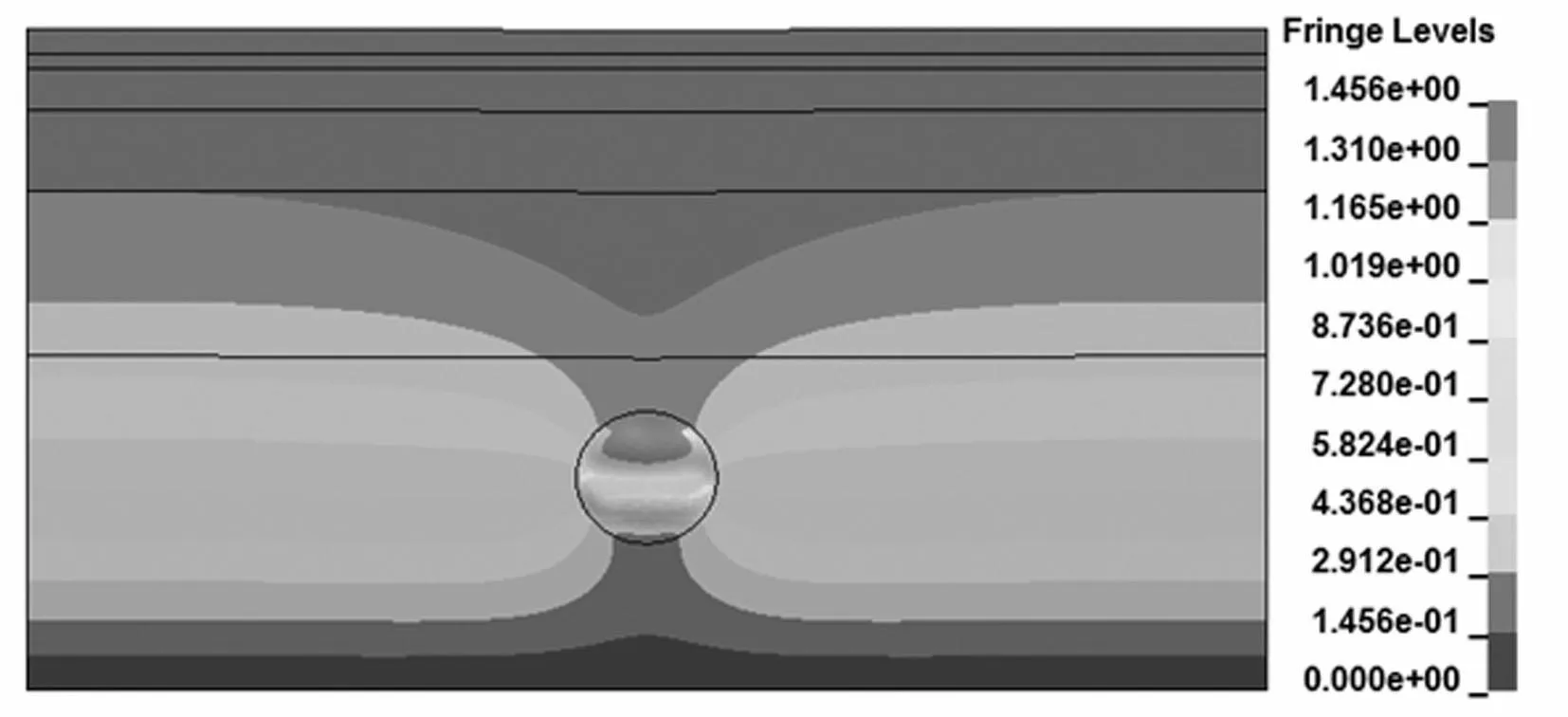
图6　土体初始沉降 Fig.6 Initial settlement of soil

图7　土体初始应力 Fig.7 Initial stress of soil

2.5屈曲分析有限元模型

在进行屈曲分析时，无需对钢环后侧衬砌等结构进行建模，以减小建模规模、节省计算时间。根据地质资料，以钢环为核心区域，采用六面体实体单元，建立钢环轴向屈曲分析的有限元模型，见图8。轴向屈曲分析有限元模型局部视图见图9，并充分考虑钢环与两侧土体间的接触关系。

图8　屈曲分析模型 Fig.8 Finite element model of buckling analysis

图9　轴向屈曲分析模型局部视图 Fig.9 Partial finite element model of axial buckling analysis

在进行侧向屈曲分析时，钢环内部土体被挖空、盾构机内部主要支撑结构被拆卸，故侧向屈曲分析有限元模型钢环内部与轴向分析时略有区别，轴向屈曲分析有限元模型局部视图见图10。

图10　侧向屈曲分析模型局部视图 Fig.10 Partial finite element model of lateral buckling analysis

3结果分析与讨论

3.1钢环前侧阻力分析

在获得了土体初始沉降及土体初始应力之后，将平衡状态时刻的土体应力场导出，作为初始应力加载；再加入盾构、钢环等内部结构，同时施加重力，计算得到盾构以及内部结构的应力形态；然后利用非线性显式动力学软件LS-DYNA模拟了钢环在土体中的顶伸过程。

随着钢环在土体中的深入，土体在钢环作用下会产生一定的流动，土体流动的速度矢量图见图11，钢环前侧土体的流动更为明显。

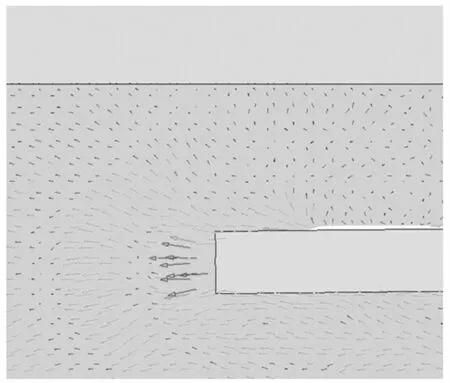
图11　土体流动速度矢量图 Fig.11 Velocity vector of soil fluid

在钢环顶推方向的前侧设置了四个压力测量点，压力时程分析时，压力值取四点的平均值，每两个测量点之间相隔90度，见图12。为保证钢环的稳定性及轴心位置的精准度，钢环顶推速度控制在1mm/s，顶伸长度为2585mm。钢环尾部在液压缸推动作用下稳速前进，为此在尾部施加相应的边界条件模拟钢环前进的过程，并保持速度的稳定，同时考虑钢环在支撑结构下的约束条件。

图12　压力测量点 Fig.12 Measuring point of pressure

见图13，随着钢环的深入，前侧压力逐渐增加，并在一定时刻达到峰值，随后有所下降，并稳定在一定范围以内。在0～700s之间，钢环前侧压力稳步增加，并在700～800s之间达到峰值，最大值约为7.9MPa，随后钢环前侧压力开始下降，并在1500s之后基本稳定，稳定在6MPa左右。

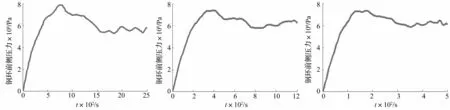
图13 压力时程曲线(v=1mm/s)Fig.13Timehistorycurveofmeasuringpressure(v=1mm/s)图14 压力时程曲线(v=2mm/s)Fig.14Timehistorycurveofmeasuringpressure(v=2mm/s)图15 压力时程曲线(v=5mm/s)Fig.15Timehistorycurveofmeasuringpressure(v=5mm/s)

当速度改变时，会对钢环前侧阻力产生一定的影响，峰值压力存在一定的区别，但最终的稳定压力基本相同。当速度为额定工况的2倍及5倍时，最大阻力约为7.4及7.2MPa，且最终稳定在6MPa左右，见图14、图15。在不同的速度下，钢环前侧压力的变化规律是一致的，盾构机顶推液压缸采用十九组千斤顶，每组的最大顶推力为15000kN，根据钢环截面积，顶推压力最大可达58.85MPa，能够满足工作需要。

3.2钢环应力应变分析

钢环在顶推过程中等效应力变化见图16～图18。随着钢环在土体中的深入，钢环等效应力逐渐增大，400s时钢环最大等效应力为38.4MPa，在875s左右时钢环等效应力达到最大值，最大等效应力为88.31MPa。随着钢环进一步的深入，钢环的最大等效应力有所下降，并基本稳定在70MPa左右。钢环最大等效应力出现在钢环前端，即与土体接触的区域。不同时刻时，钢环等效应力的分布也不尽相同，和土体初始接触时，钢环主要受前侧阻力的影响，当深入到一定深度，钢环不仅受四周土体的挤压力同时也受到土体摩擦力的影响。

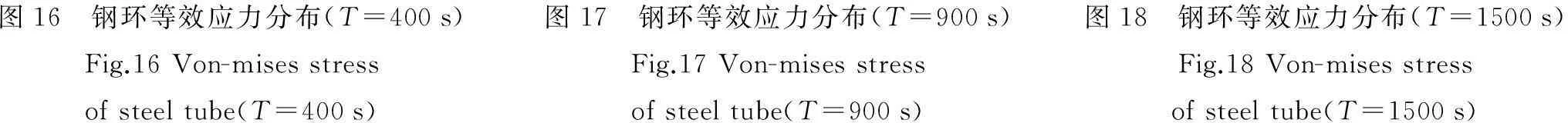
图16 钢环等效应力分布(T=400s)Fig.16Von-misesstressofsteeltube(T=400s)图17 钢环等效应力分布(T=900s)Fig.17Von-misesstressofsteeltube(T=900s)图18 钢环等效应力分布(T=1500s)Fig.18Von-misesstressofsteeltube(T=1500s)

图19 钢环位移分布(T=400s)Fig.19Displacementofsteeltube(T=400s)图20 钢环位移分布(T=900s)Fig.20Displacementofsteeltube(T=900s)图21 钢环位移分布(T=1500s)Fig.21Displacementofsteeltube(T=1500s)

钢环在顶推过程中的变形见图19～图21，放大比例因子为50倍。钢环的变形主要集中在与土体接触的区域，400s时钢环最大变形量为3.52mm，在900s时钢环最大变形量增大到6.11mm，1500s时为6.98mm。稳定后钢环的最大变形量在7mm左右。

3.3钢环屈曲失稳分析

3.3.1钢环侧向失稳分析

当盾构内部结果拆卸后，土层上部如存在大型建筑或大型工程机械装备，过大的土压力可能会导致钢环发生侧向失稳。

为此利用ANSYS软件分析了钢环侧向屈曲前十阶特征值及屈曲模态，前十阶特征值见表2，当土体上部压力超出1.57MPa时，钢环发生侧向失稳。

钢环前两阶侧向屈曲模态见图22～图23，从图中可以看出，当土体上部压力达到1.57MPa时，钢环顶部首先发生失稳。故在进行施工时，应对钢环的侧向失稳重点加以防范，避免钢环侧向承受过大的压力。

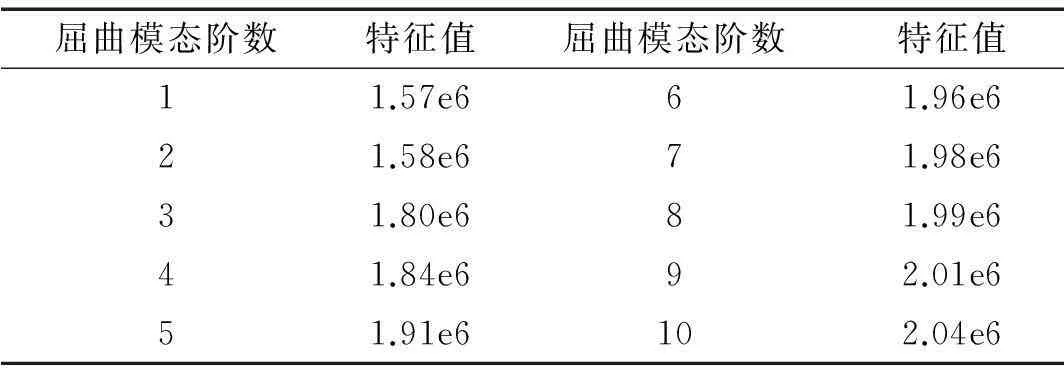
表2　钢环侧向屈曲前十阶特征值

图22　钢环侧向失稳第一阶屈曲模态 Fig.22 1st modal of steel tube lateral buckling

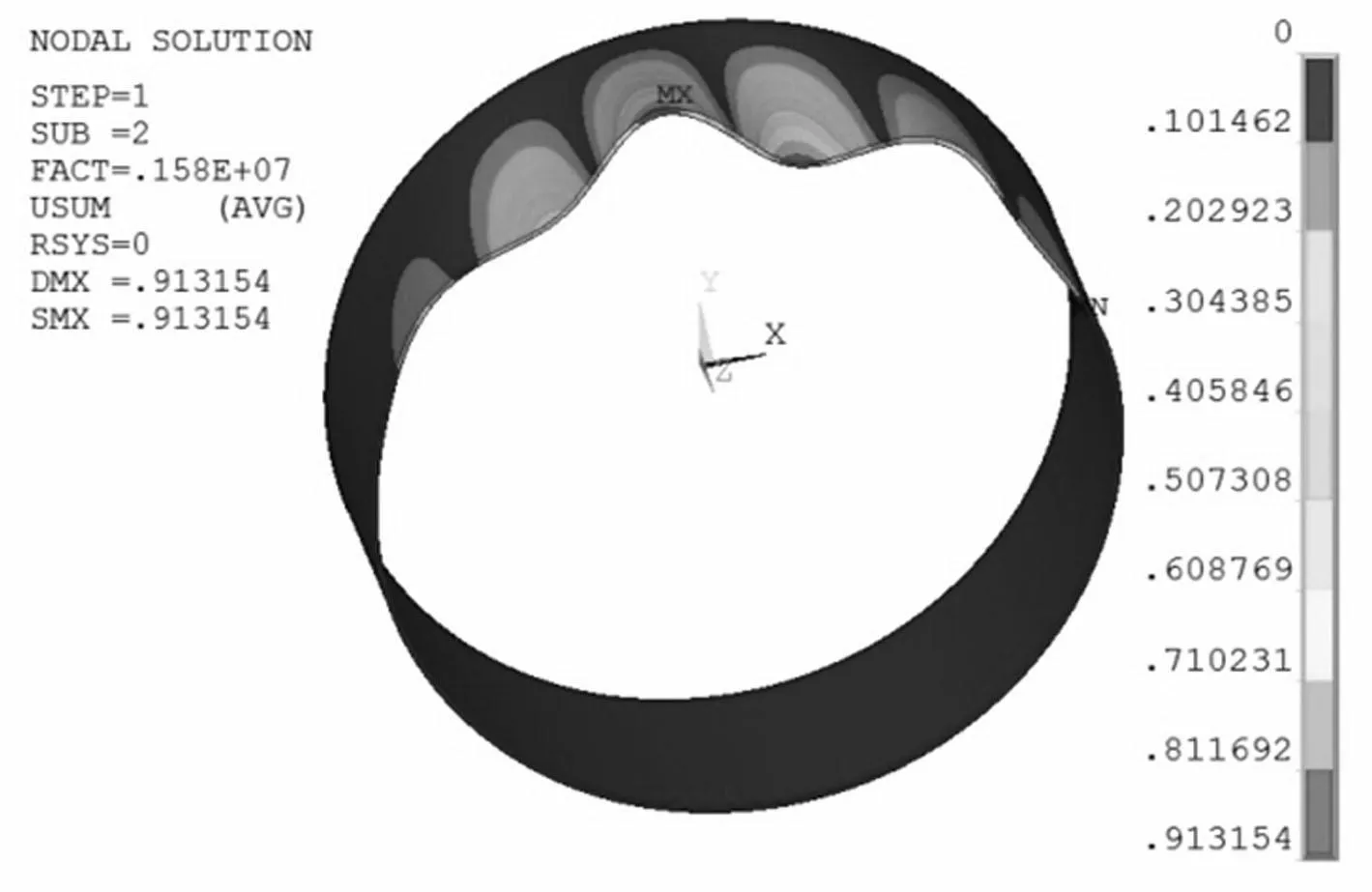
图23　钢环侧向失稳第二阶屈曲模态 Fig.23 2nd modal of steel tube lateral buckling

3.3.2钢环轴向失稳分析

在顶伸过程中，钢环后部受液压缸的驱动，前侧及侧面受土体的阻力及摩擦力，若阻力过大可能会出现轴向失稳，为此分析了轴向屈曲前十阶特征值及屈曲模态。钢环轴向屈曲前十阶特征值见表3，当顶推压力达到508MPa时，钢环发生轴向失稳。

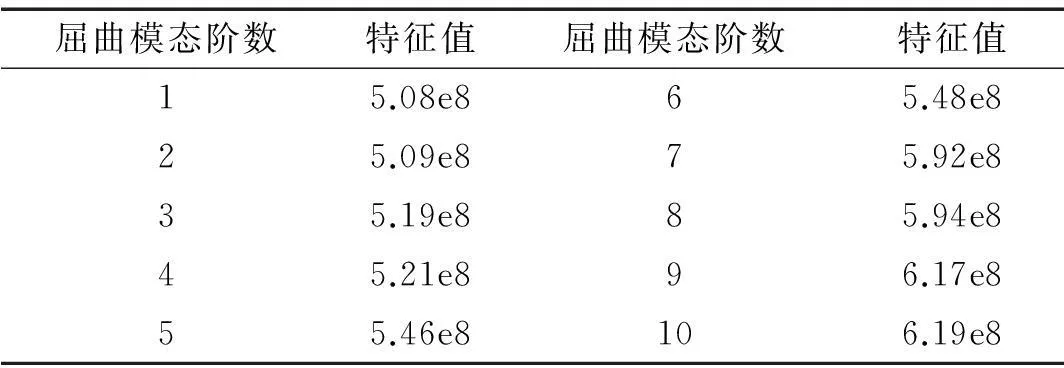
表3　钢环轴向屈曲前十阶特征值

钢环前两阶轴向屈曲模态见图24～图25，从图中可以看出，当钢环前侧阻力达到508MPa时，钢环与土体接触的前侧发生轴向失稳。此数值已超过钢环材料的屈服极限强度，并根据对钢环前侧阻力的分析，可知发生轴向失稳的可能性较小。

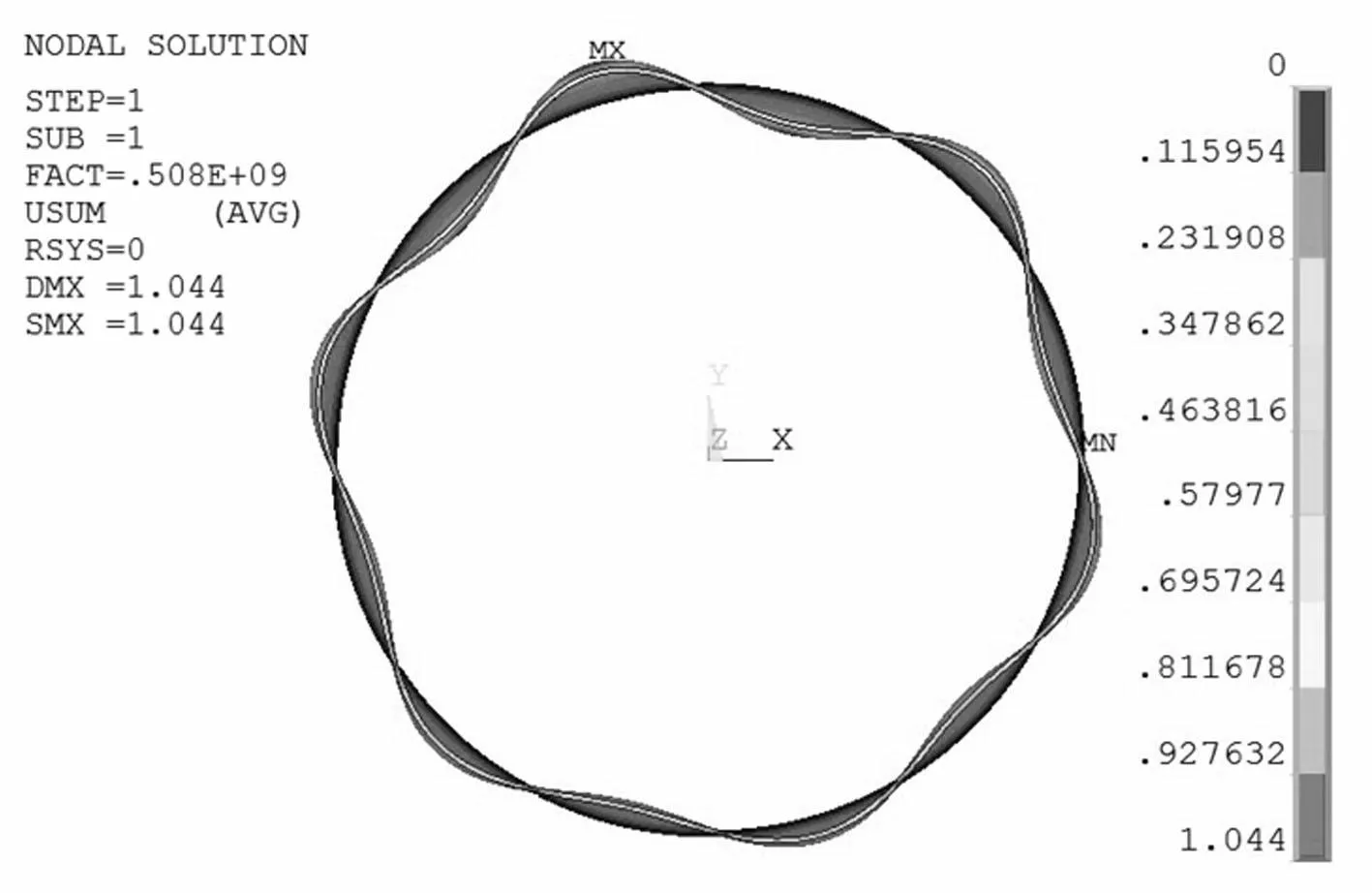
图24　钢环轴向失稳第一阶屈曲模态 Fig.24 1st modal of steel tube axial buckling

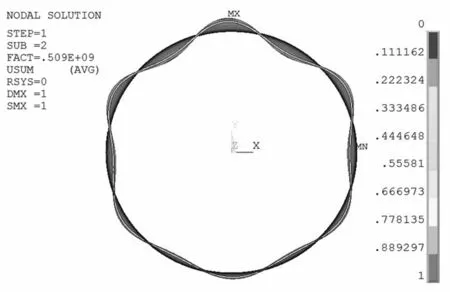
图25　钢环轴向失稳第二阶屈曲模态 Fig.25 2nd modal of steel tube axial buckling

4结论

针对大型盾构对接施工，本文基于ALE方法，模拟了盾构对接过程中钢环顶伸过程，分析了顶伸过程中钢环的应力应变状况，并对钢环的轴向及侧向的稳定性进行了分析，并得到了如下几点结论：

(1)在钢环顶伸的过程中，随着钢环的深入，前侧阻力逐渐增加，在达到峰值后开始下降，并稳定在一定范围以内；

(2)当顶伸速度提高时，钢环前侧阻力的变化规律是一致的，其峰值压力略有下降，但最终的稳定压力基本相同；

(3)钢环和土体初始接触时，钢环等效应力分布主要受前侧阻力的影响。当顶伸到一定深度，钢环不仅受四周土体的挤压力同时也受到土体摩擦力的影响，其不同时刻的最大等效应力均小于屈服极限强度。另外钢环变形主要集中在钢环前端和土体接触的区域；

(4)对于钢环的稳定性状况，钢环发生轴向失稳的可能性较小。当钢环内部土体被挖空、盾构机内部主要支撑结构被拆卸后，对钢环的侧向失稳应当重点加以关注。

参考文献

[1]王国安. 盾构地中对接施工技术初探[J]. 隧道建设，2007, 2(8):536-541.

WANG Guo-an. Preliminary study on construction technology of connecting shied machines in the ground [J]. Tunnel Construction, 2007, 2(8):536-541.

[2]洪开荣. 水下盾构隧道硬岩处理与对接技术[J]. 隧道建设，2012, 32(3):361-365.

HONG Kai-rong. Case study on hard rock treatment technology and shield docking technology in boring of underwater tunnels[J]. Tunnel Construction, 2012, 32(3):361-365.

[3]Bauer R, Leung W, Barfoot T. Experimental and simulation results of wheel soil interaction for planetary rovers [J].Intelligent Robots and Systems,2007,44(9):2852-2862.

[4]Kushwaha R L, Shen J, Barfoot T. Finite element analysis of the dynamic interaction between soil and tillage tool[J].American Society of Agricultural Engineers, 1995,38(5):1315-1319.

[5]Nezami E G, Youssef M A, Zhao D W, et al. Simulation of front end loader bucket-soil interaction using discrete element method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007,31:1147-1162.

[6]Asaf Z, Ruhinslein D, Shmulevich I. Determination of discrete element model parameters required for soil tillage[J].Soil and Tillage Esearch,2007, 92(12):227-242

[7]Fredj A, Aaron D. A 3-dimentional continuum ALE model for soil-pipe interaction[C]//7th International Pipeline Conference, Albert, 2008.

[8]Herzl C. Contact buckling and postbuckling of thin rectangular plates[J].Journal of the Mechanics and Physics of Solids,2001,49:209-230.

第一作者潘月月女，博士生,1987年生

通信作者李正农男，教授，博士生导师,1962年生

第一作者李郑发男，博士，高工，1983年8月生