有争议的碰撞恢复系数研究进展

有争议的碰撞恢复系数研究进展

姚文莉1， 岳嵘2

(1.青岛理工大学理学院，山东青岛266520; 2.山东科技大学数学与系统科学学院，山东青岛266590)

摘要：碰撞恢复系数是研究碰撞问题的重要且颇具争议的参数，对于该参数争议的焦点在于：①哪一个碰撞恢复系数的定义更合理；②碰撞恢复系数是否只与材料相关；③可否表达为其他变量的函数；④是否还存在其他更稳定的碰撞过程中的不变量；⑤不同类型的碰撞恢复系数如何应用。围绕上述焦点问题，从定义等价性、优劣、研究方法以及应用方式等各个角度进行了回顾，分析了利用碰撞恢复系数来解决碰撞问题中存在的问题，并探讨了今后的研究发展方向。

关键词：碰撞恢复系数；斜碰撞；多体系统；摩擦；瞬时冲量法

中图分类号:O313.4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.007

Abstract:Restitution coefficient for impact problems is an important and controversial parameter. The controversial problems are as follows: which definition is more appropriate among those in common use; whether or not the coefficients are only related to material of colliding bodies; whether restitution coefficients can be expressed as a function of other variables; whether is there any another coefficient with stable and constant properties during collision; how to use different types of restitution coefficients? Here, revolving around these problems, the review on impact problems was made. The existing problems were analyzed when solving the collision problems by using restitution coefficients and the future study direction was discussed.

基金项目：国家“973”计划(2011GB711106);国家“863”计划(2012AA112002)

收稿日期：2014-05-13修改稿收到日期：2014-09-25

Advance in controversial restitution coefficient study for impact problems

YAOWen-li1,YUERong2(1.School of Sciences, Qingdao Technological University, Qingdao 266520, China;2.College of Mathematics and Systems Science, Shandong University of Science and Technoloyg Qingdao 266590, China)

Key words:restitution coefficient; oblique collision; multibody system; friction; instantaneous impulse method

碰撞问题一直以来是动力学领域研究的难点和热点问题[1-4]，如果把解决碰撞问题的方法分为：瞬时冲量法，连续接触力法及有限元法这三种方法的话，碰撞恢复系数则是利用瞬时冲量法来解决刚体系统碰撞问题时所引入的必要的参数，对于只是关心碰撞前后的运动状态，而不需要了解碰撞过程中力的细节的问题而言，碰撞恢复系数的引进可以将碰撞过程中的法向及切向解耦，从而得到代数的而非微分或更为复杂的方程，这点对要求快速模拟及实时仿真控制系统的问题而言无疑具有极大的吸引力，况且不只在瞬时冲量法中，在利用连续接触力法及有限元法来解决多体系统的碰撞问题时，碰撞恢复系数的引入也有方便之处。

自从牛顿1686年提出碰撞恢复系数的定义并用来解决碰撞问题之后，这个参数一直争议不断，但并没有阻挡广大的研究者及工程师们研究及应用该系数的热情，在众多的关于碰撞问题的研究文献中，本文提炼出关于碰撞系数的争议性的问题，从定义的方式、优劣、研究方法以及应用方式等各个角度进行了回顾及分析，并总结了对碰撞恢复系数未来研究的方向。

1碰撞恢复系数的定义研究

1.1三类定义方式

文献中出现了各种不同的碰撞恢复系数定义方法，按该系数的定义所表现的物理性质，一般可以将其划分以下为三类：

(1)运动学恢复系数

(1)

(2)动力学碰撞恢复系数

牛顿所提出的运动学的恢复系数直接给出了碰撞前后的运动学关系，Poisson认为碰撞中之所以会发生运动速度的变化，是因为力的作用效应，故将碰撞力的冲量引入了定义。他提出用碰撞的恢复阶段和压缩阶段的作用冲量之比作为恢复系数的定义：

(2)

(3)能量恢复系数

碰撞过程是能量损耗的过程的，一些研究者更倾向于从能量的角度来定义碰撞恢复系数[5-10]，其中最著名的还属Stronge所提出的能量恢复系数，他同样将碰撞过程分为压缩和恢复两个阶段：

(3)

1.2三类碰撞恢复系数的等价性的研究

三种碰撞恢复系数等价性的问题一直受到关注，多位学者研究了这个问题。

Stronge[6]认为在粗糙的且斜碰撞过程中滑动方向改变的情形下三种恢复系数是不等价的，而当物体碰撞发生在对心碰撞、正碰撞、光滑碰撞或者是粗糙斜碰撞中滑动方向不改变的任何一种情形下，三种恢复系数都是等价的;Stronge[11]在考虑五种滑动模式的情况下，通过碰撞法向冲量为变量研究了含摩擦的两个硬物体斜碰撞问题，并得到了三种恢复系数之间特殊的解析联系式，且再次显示：在斜碰撞情形下，只有滑动是单向的情况，这些系数才是等价的。

对于同样的问题，吕茂烈等[16-17]以冲量形式给出了等价的条件。

上述研究均是针对两个刚体的碰撞问题，“在两个刚体的光滑碰撞问题中，三种恢复系数等价”的结论是有共识的，但当研究多体系统的多点碰撞问题时，Pfeiffer[18]的计算表明：即使碰撞是对心光滑的正碰撞情形，用运动学及动力学恢复系数计算的结果也不同。

总之，三种恢复系数不能相互替代，只有在满足一定的条件下才会等价。

1.3三类恢复系数的优劣讨论

碰撞本身是以速度跳断的方式体现的，牛顿的运动学恢复系数直接以碰撞前后速度关系的形式出现，定义最为直接且实验容易测定；速度突变的根本原因在于力的极短时间内的累积效应，即碰撞力的冲量，Poisson的动力学恢复系数是从冲量的角度来定义碰撞过程，Kilmister等[20]认为从哲学意义上来讲，Poisson更为合理；而碰撞本身是一个能量消耗的过程，从能量耗散的角度来定义碰撞也更能体现碰撞的本质，因此，三类恢复系数从碰撞作用不同的角度来定义，各有特点。

从系数本身的特性及实用的角度来讲，三类碰撞恢复系数究竟哪一种更优呢？这涉及到按照什么样的标准来评判最优的问题。文献中对该问题的研究主要是从以下两个方面来进行：

(1)哪类恢复系数的数值在碰撞过程中更接近于常数

不管哪一类恢复系数，最初对于恢复系数的定义都是希望能够得到稳定的只与材料有关的常数，因此，恢复系数在碰撞过程中是否接近于常数及对初值的敏感性如何，成为判断的主要标准。

Andrés等[21]研究了细长杆与粗糙的地面相碰撞的情形，分别通过三种恢复系数的刚体模型及考虑法向、切向柔度及滑动黏滞效应的弹簧振子模型进行了研究，研究发现当弹簧刚度k→∞时，相比另外两种恢复系数而言，采用能量恢复系数下的刚体模型计算得到的碰撞后角速度及能量损耗与局部柔化下的更一致。

姚文莉[22]采用同样的例子，研究了三种恢复系数对初始角的敏感度问题，相对不同的入射角，Stronge能量恢复系数的曲线非常密集，且呈单调关系，而Newton运动学和Poisson动力学恢复系数则变化明显，即对入射角的敏感度较大。相对Newton及Poisson恢复系数，Stronge恢复系数表达式对初值的微小变化具有更好的稳定性。

(2)能否保证碰撞前后的能量协调

Kane[23-24]在将牛顿运动学恢复系数及Whittaker假定综合应用来解决一般多刚体系统碰撞问题时，针对某些初始条件，计算中出现了碰撞后动能增加的奇怪现象，随后，他以 “一个动力学之谜”为题，将碰撞计算中所发生的能量不协调的问题提了出来；而Seabra等[25]采用了运动学恢复系数，通过角坐标及正则方程在模拟双摆问题时，同样遇到碰撞后能量增加的不协调的问题。

这个问题使得很多研究者对于用简单的Newton恢复定律来解决含摩擦的一般多刚体碰撞问题的方法发生了怀疑，是否碰撞前后能够保证能量协调成为判断碰撞恢复系数优劣性的重要标准。

Wang等[26]研究了含摩擦两维刚体的碰撞问题，他们考虑了可能的碰撞模式，分别选用了Newton恢复定律及Poisson恢复定律来计算碰撞后的能量，在简单的杆与粗糙地面的斜碰撞问题中，发现Newton恢复系数依然会出现能量不协调问题，而Poisson则不能；Ivanov[9]分别用三种恢复系数研究两体碰撞问题，通过将分析结果与实验结果相对比，他认为能量恢复系数更有实际意义。

Stronge[15]在提出新的能量恢复系数之后，采用三种恢复系数重新计算了Kane的算例后发现：虽然通过动力学恢复系数计算的碰撞后能量损失总是为负值，但它相比于能量恢复系数，耗散了过多的能量,于是他认为：在三种关于恢复系数的定义中，能量恢复系数是唯一与能量协调的。

关于恢复系数优劣性的争论一直在持续，Djerassi[12-14]在近年的连续三篇文章中，分别基于三种不同的恢复系数，采用Routh的半图解方法及库仑摩擦模型，研究了简单非完整系统的单点碰撞问题，结果显示:当碰撞过程中有粘滞或反向滑动发生时，Routh方法的并入并不能阻止采用Newton恢复系数时所带来的动能增加，对于Poisson假定而言，系统存在唯一、能量一致的解，而同样采用Stronge的能量恢复系数时则应用范围明显变窄。

Stronge针对上述观点进行了回应，他认为上述观点的原因在于作者误解了能量恢复系数的物理含义而在系统上强加了由Poisson系数表达的冲量比的人工约束。对于含摩擦的斜碰撞而言，三种定义的恢复系数会得到碰撞后速度及能量损耗的不同结果，当三者取值相同时，三种定义下恢复系数产生的能量改变满足ΔEp≤ΔEs≤ΔEN(其中ΔEp、ΔEs、ΔEN分别代表Poisson、Stronge及Newton恢复系数下的碰撞中的动能损失), 采用eN会产生动能的增加，因而违背能量守恒；采用ep，则因在恢复阶段计算了过多的法向接触冲量的功而导致系统损耗了比实际更多的能量，只有在采用es计算时，才可以得到系统碰撞前后能量的守恒。

按上述标准来看，相比另外两类恢复系数，能量的恢复系数es更稳定且符合能量守恒，但因其表达的复杂性，使得在多体系统的实际应用中，eN及ep仍然得到广泛的应用。

2碰撞恢复系数与其他因素的相关性

碰撞恢复系数是表明碰撞过程的宏观简化量，当细化碰撞过程时，根据现有的恢复系数的定义，恢复系数都不会只是与材料有关的常数。实验及有限元数值计算都表明除了碰撞材料的特性，它还与一些其他因素有关，如碰撞点的初始速度、碰撞位形[27-29]、碰撞物体表面的分形参数[30]、因强烈的振动效应导致的多个连续碰撞次数[31]、多体系统的连接方式[32]等, 恢复系数对上述因素的依赖作用可以通过实验验证、有限元方法或固体接触力学方法解析计算。

2.1恢复系数与其他变量的依赖模型

既然碰撞恢复系数已被证明是与碰撞速度等相关，那么现有的恢复系数与这些因素的解析模型的建立是恢复系数能够有效运用的方法之一。

Goldsmith[33]指出：如果碰撞时间比物体的最低本征周期长，那么波的效应可以忽略，碰撞可以用准静态接触理论来考察。借助于接触力学中不同的力与位移关系模型，得到了碰撞恢复系数与其他因素依赖关系的不同形式的解析表达式：

(1)弹塑性球之间的碰撞模型[27]

(4)

式(4)中采用牛顿恢复系数计算，Vy是法向相对碰撞速度的屈服界限(在此之下假设碰撞是弹性的)，该式体现了恢复系数与碰撞初始相对速度的依赖关系。

(2)能量恢复系数表达式[8]

(5)

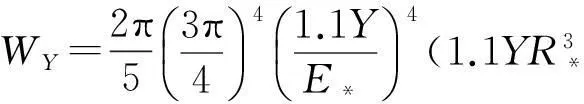
(3)单点多体系统斜碰撞问题的能量恢复系数[32]

(6)

式中,λ1，λ2，λ3及λ4是碰撞物体相对碰撞角度、速度及摩擦的函数，f为接触力与位移的关系模型，只与碰撞物体的材料特征相关，该表达式显示了能量恢复系数对碰撞物体的材料、碰撞位形、速度、切向特征及多体系统连接方式之间的依赖关系。

2.2恢复系数的修正模型

碰撞恢复系数的最初引入其实是为了得到一个在碰撞过程中的只与材料相关的宏观不变量，从而简化计算。但如前节所阐述的：即使是相对稳定的Stronge能量恢复系数也不是只与材料有关的常数，那么是否能通过对现有系数的修正，使其等于或接近于常数呢？

碰撞过程中会造成能量的损失，能量损失主要来源于波传播、塑性变形及摩擦。对于细长的杆件、薄的壳体而言，大部分的初始动能都被转变为因碰撞产生的波。如：Zener[34]析了球对固定梁的完全弹性碰撞问题，其中高达90%的动能转变为波；即使是致密的物体，当碰撞物体之间的材料及大小相差过大时，因碰撞所导致的振动波散失的能量也不可忽略，Lim等[35]研究了粗糙的圆柱体与地面的斜碰撞问题，当碰撞速度取系统的塑性变形的初始速度临界值时，以波的形式散失的能量达到48%或46%，Schiehlen[36]在弹性碰撞的数值及实验研究中，展示了碰撞物体的形状对波的能量损失的作用。

Stronge的能量恢复系数的定义中并没有考虑碰撞引起的波动及振动所带来的能量损失，这是能量恢复系数非常数的主要因素，因此，对能量恢复系数e*定义的修正如下：

(1)合并波动效应[35]

(7)

式中,Ww代表因应力波所造成的能量散失，其数值可根据接触力与位移的特征预先算出；

(2)合并模态振动效应[10]

(8)

式中,T0为系统初始能量，PE，DE及FEi分别为系统应变能、动能及碰撞力能量。

(3)包含碰撞局部及整体能量损失[9]

e*=eL⊕eS

(9)

式中针对细长杆件与地面斜碰撞问题，其中es代表法向局部能量损失，eL代表整体的振动能量损失，二者非简单的加法，而是代表能量效应上的叠加。

3恢复系数在碰撞动力学计算中的应用方法

碰撞动力学计算一般可分为三种方法：瞬间冲量法；连续接触力模型；有限元方法。碰撞恢复系数是利用瞬时冲量法来解决刚体系统碰撞问题时所引入的必要的参数，不只在瞬时冲量法中，在利用连续接触力法及有限元法来解决多体系统的碰撞问题时，碰撞恢复系数的引入也有它的方便之处。本文按是否考虑其对其它参数的依赖性，将其在计算中的应用方法分为以下两种：

3.1将碰撞恢复系数作为材料常数

(1)在瞬间碰撞假定模型中的应用

这种应用方式是碰撞恢复系数最常见、广泛的应用方法。最初，牛顿首次提出用运动学恢复系数来作为碰撞动力学问题的补充方程，首次解决了近球状物体的对心正碰问题；Kane第一次大胆的将牛顿恢复系数与Witterker假定相结合应用到一般多刚体系统的斜碰撞问题中，但遇到了“Kane的动力学之谜”，使得研究者重新思考斜碰撞中恢复系数及切向模式问题；Feiffer采用Poisson动力学恢复系数，将多体系统的多点斜碰撞过程通过线性互补性关系(LCP)表达出来; Stronge[37]采用能量恢复系数研究了多体系统的单点斜碰撞问题。

(2)与弹簧振子模型的阻尼系数间的联系

Johnson[38]认为：当碰撞速度比波的传播速度小的时候，碰撞处的切向和法向柔度可以用无质量的弹簧来模拟。因为一般波速在46m/s(橡胶)和5200m/s(钢)之间，而本文主要涉及的是不引起结构损坏的低速碰撞问题，故上述条件是很容易达到的。

一般采用的非线性弹簧阻尼模型：

(10)

(11)

Carbonelli等[40]也研究了反弹球问题中弹簧振子模型与碰撞恢复系数的关系。

(3)作为连续接触力模型中碰撞结束的标准

Liu等[41-44]在一系列文章中，引入弹性力与位移关系，同时用能量恢复系数作为碰撞结束的标准研究了多点碰撞问题，该方法在一些刚体碰撞的难点问题上取得了与实验相吻合的结果。

3.2考虑碰撞恢复系数对其他参数的依赖性

如在第3节中所述，恢复系数不只是材料常数，而且与初始条件等因素相关，因此一些研究者在利用恢复系数来解决碰撞问题时，考虑了恢复系数的非常数特征。

(1)直接采用与初始条件相关的恢复系数解析表达式

在考虑轴承间隙的机械动力学问题中，Stammers等[45-46]均采用了速度依赖的碰撞恢复系数：

e=1-0.26v1/3

(12)

Yao等[32]在单点多体系统碰撞问题中采用了解析形式的能量恢复系数，并得到了能量协调的碰撞后的速度。

(2)直接通过有限元方法计算恢复系数的数值

Schiehlen[47]在含碰撞的多体系统的计算中采用了多尺度的方法，即先采用Poisson的动力学恢复系数来表达碰撞过程中的总冲量，然后利用有限元的方法精细地计算Piosson动力学恢复系数，最后返回到慢尺度中继续多体系统的计算过程。这种模拟的方式并非预先给定恢复系数的数值或表达式，优点在于可以相对精确的计算恢复系数，缺点在于增加了计算时间。

4结论

对于含多点碰撞的复杂系统(如：数以万计的颗粒相互接触、碰撞的系统)而言，引入碰撞恢复系数所能带来的计算效率的提高是至关重要的，而为保证计算精度，对碰撞恢复系数进行深入研究是必要的。到目前为止，对于碰撞恢复系数的研究工作可达成以下共识：

(1)现有定义的碰撞恢复系数均不是只与材料有关的常数，目前对恢复系数的修正工作主要是从能量损耗的角度入手，找到碰撞中的不变量；

(2)关于碰撞恢复系数与其他变量的关系表达式主要是基于力与位移关系，其精确度依赖于力与位移关系的建立模型，且目前所得到的表达式均过于复杂，从而给其在复杂系统中的应用带来了不便；

(3)碰撞恢复系数性质的研究还主要集中在两个物体单点碰撞之间，当碰撞点增多时，各个接触处恢复系数之间的耦合作用的研究甚少。

碰撞恢复系数是碰撞研究中最为基础性的工作，目前的工作虽然有一定的进展，但远未成熟，针对研究现状，我们认为今后对碰撞恢复系数的研究工作可以在以下几方面寻求突破:

(1)从更多的角度寻找碰撞过程中不变量，得到碰撞恢复系数的更合适的定义方式；

(2)将碰撞恢复系数的研究从两点向多点扩展，考虑因多个碰撞点动力学效应的相互耦合所带给碰撞恢复系数的影响；

(3)碰撞恢复系数是极强短暂的碰撞作用的宏观简化，而接触力学有限元数值及实验设计的精确度是这个简化的基础，有效利用计算接触力学及碰撞实验研究的最新研究成果，碰撞恢复系数的研究有望取得突破。

本文主要关注了碰撞中的法向特征，文中的碰撞恢复系数也是指法向碰撞恢复系数，当考虑碰撞的切向特征时，工程中一般会采用库仑的干摩擦模型，也有学者提出了切向恢复系数的概念来表征切向柔度，但因切向恢复系数在应用中远远不如法向碰撞恢复系数那么广泛，故文中没有过多阐述。

参考文献

[1]Brogliato B. Nonsmooth Mechanics[M]. Berlin:Springer, 1999.

[2]董富祥,洪嘉振. 多体系统动力学碰撞问题研究综述[J].力学进展, 2009, 39(3)：352-359.

DONG Fu-xiang, HONG Jai-zhen. Reviewof impact problem for dynamics of multibody system[J]. Advances in Mechanics, 2009, 39(3): 352-359.

[3]姚文莉,王育平,边力,等. 多刚体系统接触碰撞动力学研究进展[J].力学与实践, 2007, 29(6):9-12.

YAO Wen-li, WANG Yu-ping, BIAN Li,et al. Survey for dynamics on impact and contact of multi-rigid-body systems[J]. Mechanics in Engeneering, 2007, 29(6):9-12.

[4]Khulief Y A. Modeling of impact in multibody systems: an overview[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8:1-15.

[5]Boulanger G. Note sur le choc avec frottement des crops non parfaitment elastique[J]. Revue Science,1939, 77:325-327.

[6]Stronge W J. Rigid body collisions with friction[J]. Proceedings of Royal Society of London, 1990, A431:169-181.

[7]Stronge W J. Friction in collisions: resolution of a paradox[J]. Journal of Applied Physics,1991, 69(2):610-612.

[8]Stronge W J. Impact mechanics[M]. Cambridge: Cambridge University Press, 2000.

[9]Ivanov A P. Energetics of a collision with friction[J]. Journal of Applied Mathematics and Mechanics,1992, 564:527-534.

[10]Wagg D J. A note on coefficient of restitution models including the effects of impact induced vibration[J]. Journal of Sound and Vibration,2007, 300:1071-1078.

[11]Stronge W J. Smooth dynamics of oblique impact with friction[J]. International Journal of Impact Engineering, 2013, 51: 6-49.

[12]Djerassi S. Collision with friction; Part A: Newton’s hypothesis[J]. Multibody System Dynamics, 2009, 21:37-54.

[13]Djerassi S. Collision with friction; Part B: Poisson’s and stronge’s hypothesis[J]. Multibody System Dynamics,2009, 21:55-70.

[14]Djerassi S. Stronge’s hypothesis-based solution to the planar collision-with friction problem[J]. Multibody System Dynamics,2010, 24:493-515.

[15]Stronge W J. Comment:Collision with friction; Part B: Poisson’s and stronge’s hypothesis[J]. Multibody System Dynamics,2010, 24:123-127.

[16]吕茂烈. 碰撞恢复系数及其测定[J]. 固体力学学报,1984, 3: 318-329.

LÜ Mao-lie. Coefficients of restitution of their measurement [J]. ACTA Mechanica Solida sinica,1984, 3:318-329.

[17]张九铸. 一般运动刚体的恢复系数公式的适用条件[J]. 力学与实践,2010, 32(3):116-117.

ZHANG Jiu-zhu. The suitable situation of formula of coefficient of restitution for general rigid body of motion[J]. Mechanics in Engineering,2010, 32(3):116-117.

[18]Pfeiffer F. Multibody systems with unilateral constraints[J]. Journal of Applied Mathematics and Mechanics,2001, 65(4): 665-670.

[19]Pfeiffer F, Foerg M, Ulbrich H. Numerical aspects of non-smooth multibody dynamics[J]. Computer. Methodsin Applied Mechanics and Engineering, 2006, 195:6891-6908.

[20]Kilmister C W, Reeve J E. Rational Mechanics[M].Upper Saddle River, NJ:Prentice Hall Press, 1966.

[21]Andrés K, Jens L. Rigid and elastic approaches for the modelling of collisions with friction in multibody system[J]. ZAMM. Z.Angew.Math.Mech., 1996, 76:243-244

[22]姚文莉. 含摩擦的多刚体系统动力学问题的研究[D].北京：北京大学, 2005.

[23]Kane T R. A Dynamics Puzzle[N]. Stanford Mech Alumni Club Newsletter, 1984.

[24]Kane T R, Levinson D A. Dynamics: Theory and applications[M]. New York:McGraw-Hill, 1985.

[25]Seabra M，Nikravesh P. Impact dynamics of multibody systems with frictional contact using joint coordinates and canonical equations of motion[J]. Nonlinear Dynamics,1996, 9: 53-71.

[26]Wang Y, Mason M T. Two-dimensional rigid-body collisions with friction[J]. ASME Journal of Applied Mechanics. 1992, 59:635-642.

[27]Thornton C. Coefficient of restitution for collinear collision of eelastic spheres[J]. ASME Journal of Applied Mechanics, 1997, 64: 383-386.

[28]Zhang X, Voc V Q. Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisions[J]. International Journal of Impact Engineering, 2002, 27: 317-341.

[29]Wu Chuan-yu, Li Long-yuan, Thornton C. Rebound behaviour of spheres for plastic impacts[J]. International Journal of Impact Engineering,2003, 28: 929-946.

[30]Lu C J, Kuo M C. Coefficients of restitution based on a fractal surface model[J]. ASME Journal of Applied Mechanics, 2003, 70:339-345.

[31]Hurmuzlu Y. An energy based coefficient of restitution for planar impact of slender bars with massive external surfaces[J]. ASME Journal of Applied Mechanics, 1998, 65(4):952-962.

[32]Yao Wen-li, Chen Bin, Liu Cai-shan. Energetic coefficient of restitution for planar impact in multi-rigid-body systems with friction[J]. International Journal of Impact Engineering, 2005, 31:255-265.

[33]Goldsmith W. Impact: The theory and physical behaviour of colliding solids[M]. London:Edward Arnold Ltd., 1960.

[34]Zener C, Feshbach. A method of calculating energy losses during impact[J]. J. Appl. Mech. H. 1939, 61:A67-A70.

[35]Lim C T, Stronge W J. Oblique elastic-plastic impact between rough clinders in plane strain[J]. International Journal of Engineering Science,1999, 37: 97-122.

[36]Schiehlen W, Seifried R. Three approaches for elastodynamic contact in multibody systems[J]. Multibody System Dynamics, 2004, 12: 1-16.

[37]Stronge W J. Generalized impulse and momentum applied to multibody impact with friction[J]. Mechanics of Structure Machines, 2001, 29(2):239-260.

[38]Johnson K L. Contact Mechanics[M]. Cambridge:Cambridge University Press, 1985.

[39]Lankarani H M，Nikravesh P E. Continuous contact force models for impact analysis in multibody systems[J]. Nonlinear Dynamics, 1994, 5:193-207.

[40]Carbonelli A, Perret-Liaudet J, Rigaud E, et al. Investigation of restitution coefficient and spring-damper models for the bouncing ball problems[C]//Proceedings of the ASME International Design Engineering Technical Conferences, IDETC/CIE. Washington D C, Paper No. DETC2011-47870, 2011.

[41]LIU Cai-shan, ZHAO Zhen, Brogliato B. Frictionless multiple impacts in multibody systems. Part I: Theoretical Framework[J]. Proedings of the Royal Solciety A: Mathematical, Physical & Engineering Sciences, 2008, 464(2100): 3193-3211.

[42]Liu C S, Zhang, K,Yang L. Normal Force-Displacement Relationship of Spherical Joints With Clearances[J]. ASME Journal of Computational and Nonlinear Dynamics, 2006, 1: 161-167.

[43]Liu Cai-shan, Zhao Zhen, Brogliato B. Frictionless multiple impacts in multibody systems. Part II: Numerical algorithm and simulation results[J]. Proceedings of the Roual Society A:Mathematical, Physical & Engineering Sciences,2009, 465(2101):1-23

[44]赵振,刘才山,陈滨. 步进冲量法[J].北京大学学报:自然科学版,2006, 42(1):41-46

ZHAO Zhen, LIU Cai-shan, CHEN Bin. Stepping-forward impulse method[J]. Acta Scientiarum Naturalium Universitatis Pekinensis. 2006, 42(1):41-46.

[45]Stammers C W, Ghazavi M. A theoretical and experimental study of the dynamics of a four-bar Chain with bearing clearance: pin motion, contact loss and impact,” [J]. Journal of Sound and Vibration, 1991, 150(2): 301-315.

[46]Herbert R G, Mcwhannel D C. Shape and frequency of pulses from an impact pair [J]. ASME Journal of Manufacturing Science and Engineering, 1997,99(3): 513-518.

[47]Schiehlen W, Seifried R, Eberhard P. Elastoplastic phenomena in multibody impact dynamics[J]. Computet Methodsin Applied Mechanics and Engineering, 2006, 195: 6874-6890.

第一作者张波男，博士生，1988年生

通信作者曾京男，教授,博士生导师，1963年生