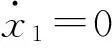两自由度含间隙弹性碰撞系统的颤碰运动分析

两自由度含间隙弹性碰撞系统的颤碰运动分析

朱喜锋1,2， 罗冠炜2

(1. 兰州交通大学 机电工程学院, 兰州 730070； 2. 甘肃省轨道交通装备系统动力学与可靠性重点实验室, 兰州 730070)

摘要：利用数值仿真方法，对一类两自由度含间隙弹性碰撞系统的动力学特性做了深入研究，分析了系统周期运动及其参数存在区域，并揭示了系统的颤碰运动特性。首先，详细分析了激振频率和系统间隙等关键参数对系统周期运动及存在区域的影响。其次，在小间隙低频工况下，数值计算了系统p/1周期运动序列及其存在区域。最后，得出随着激振频率的递减，p/1运动的碰撞次数p因擦边分岔而逐一增加，当p/1运动的碰撞次数p足够大时，系统呈现出颤碰特性，总结了系统由1/1周期运动到颤碰运动的转迁规律。

关键词：振动；颤碰；周期运动；分岔；存在区域

中图分类号:O322文献标志码：A

基金项目：国家自然科学基金资助项目(51205294,61271008)

收稿日期：2014-05-04修改稿收到日期：2014-07-23

Chattering-impact motion of a 2-DOF system with clearance and soft impacts

ZHUXi-feng1,2,LUOGuan-wei2(1. School of Mechatronic Engineering Lanzhou Jiaotong University, Lanzhou 730070, China;2. Gansu Provincial Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment, Lanzhou 730070, China)

Abstract:A 2-DOF system with clearance and soft impacts was considered. Its existence region of periodic motion and chattering-impact characteristics were analyzed with the numerical simulation method. Firstly, the influences of key parameters of the system, such as, exciting frequency and clearance on its existence region of periodic-impact motion were studied in detail. Secondly, the sequence of p/1 motion and its existence region under a small clearance and a low exciting frequency were investigated using numerical simulation. Finally, a series of grazing bifurcations occurred with decrease in exciting frequency so that the impact number p of p/1 motions correspondingly increased one by one. When the impact number p of p/1 motions became big enough, the chattering-impact characteristics appeared. The transition law from 1/1 motion to chattering-impact motion via grazing bifurcation with decrease in exciting frequency was summarized explicitly.

Key words:vibration; chattering-impact; periodic motion; bifurcation; existence region

机械系统零部件之间的间隙和约束可导致冲击振动的发生，从而使机械装备成为一个非光滑的动力学系统，运动过程也呈现出倍周期分岔、Grazing分岔和混沌等复杂动力学特性。为了降低噪音和削弱颤振的影响，在实际机械系统零部件碰撞面间常设置具有缓冲作用的弹性碰撞面，如齿轮传动系统、压力安全阀和开关电路等。Shaw等[1]利用传统理论研究了一类单自由度振动冲击系统的周期碰撞运动、鞍结分岔、多吸引子共存及混沌等复杂动力学现象，发现了振动冲击系统中存在Grazing分岔等特殊现象，并可以导致Poincaré碰撞映射奇异性。Nordmark[2]提出了研究分段线性系统和振动冲击系统的Grazing动力学及其伴随分岔的系统方法。李健等[3]研究了非光滑系统吸引子及其吸引域的计算方法。运用不连续映射方法，分析了振动冲击系统在多维Grazing分岔临界点的多种复杂动力学特征和余维二分岔[4-6]。研究结果可用于指导实用性机械装置的设计，Wen等[7]设计了沿导轨运行的弹簧振子实验装置，模拟出周期碰撞运动及其分岔。吕小红等[8]分析了小型振动冲击式打桩机的吸引子共存现象及其吸引域，得出低频下颤碰运动使桩体的渐进效果最好。俞翔等[9]通过实验研究发现，将碰撞振动子系统引入到隔振系统可有效抑制被隔振设备的振动。随着研究的不断深入，国内外学者开始重点关注系统参数与动力学特性之间的关系，Peterka等[10]分析了单自由度弹性碰撞系统亚谐运动的稳定性及存在区域。Luo等[11-12]以含间隙和刚性约束的两自由度周期激励系统为研究对象，详细分析了周期运动的多样性及其演化规律，重点揭示了系统动力学特性与关键参数之间匹配规律。

近年来，国内外学者对振动冲击系统的动力学研究大多是基于单参数分岔，对非线性系统颤碰及其转迁规律的研究较少。本文通过建立一类两自由度含间隙弹性碰撞系统的力学模型，构造了两种Poincaré映射，采用数值仿真方法，在(ω,δ)关键参数平面上详细分析了系统的周期运动及参数存在区域，得出了系统在小间隙低频工况下，由1/1周期运动到颤碰运动的转迁规律。

1力学模型

图1所示的力学模型为一类两自由度含间隙弹性碰撞系统的典型代表，两质量块的质量分别用M1,M2表示，位移用X1,X2表示，两质量块之间由刚度为K1的线性弹簧和阻尼系数为C1的线性阻尼器相连。质块M2由刚度为K2的线性弹簧和阻尼系数为C2的线性阻尼器固定于支承面，作用在两质量块上的简谐激振力为Pisin(ΩT+τ)(i=1,2)。当激振力幅值较小时，系统属于简单的线性振子；随着激振力幅值的增加，当质量块M1的位移等于间隙B，即X1=B时，M1与固定于支承的刚度为K0的弹性约束碰撞。弹性约束的刚度K0可以在[0, ∞)区间取值，因弹性碰撞的存在，使原本分段线性的系统变成一个具有复杂动力学行为的冲击碰撞系统。为使分析具有一般性，引入以下无量纲量：

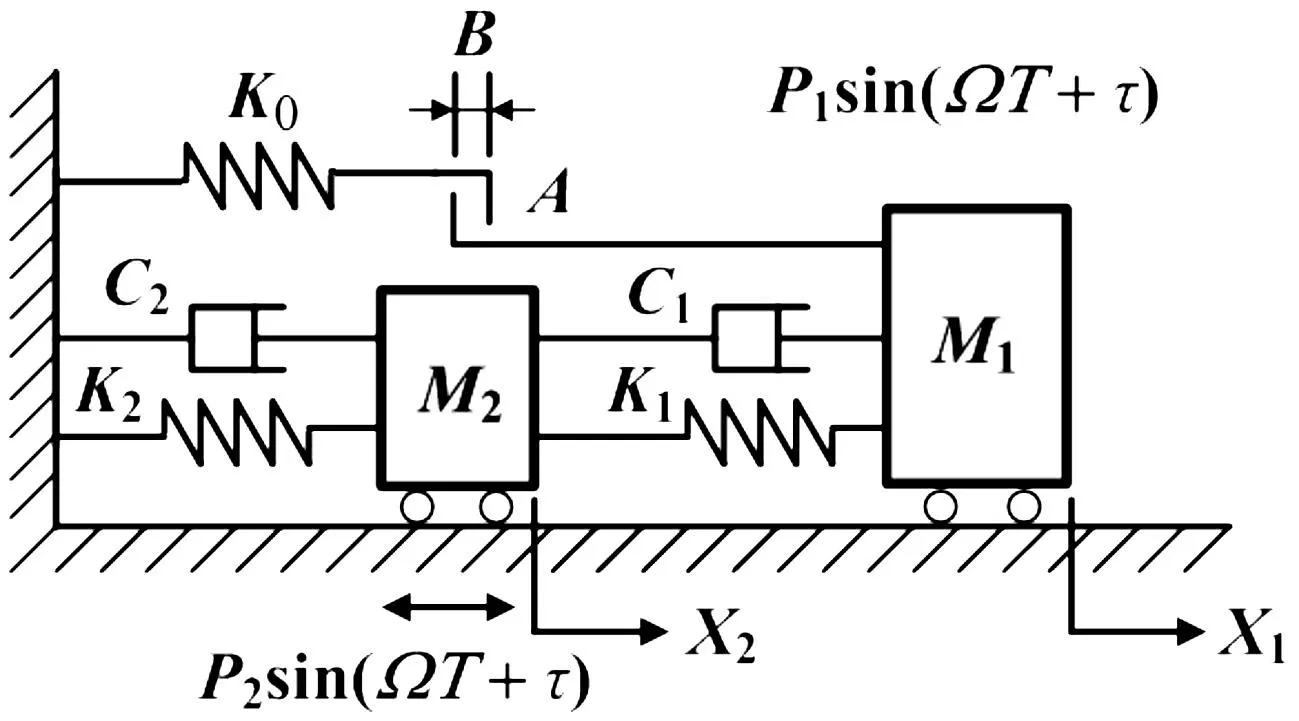
图1　两自由度含间隙弹性碰撞系统的力学模型 Fig.1 Mechanical model of a two-degree-of-freedom system with clearance and soft impact

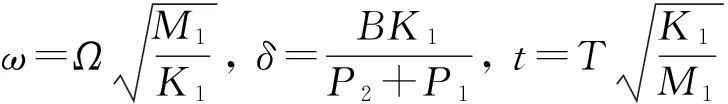
(1)

由方程(1)可得，系统参数的取值范围为：μm∈(0,1),μk∈(0,1),μc∈(0,1),μk0∈[0,1),f20∈[0,1]。图1所示两自由度含间隙弹性碰撞系统的无量纲运动微分方程为：

(2)

其中，

(3)

用符号q=p/n表示系统相应的周期碰撞运动，p=0, 1, 2, 3,…表示碰撞次数，n=1, 2, 3,…表示周期数。当间隙δ较大或激振力幅值较小时，系统为无碰撞的线性振子，用q=0，即p=0表示无碰撞运动。

(4)

2周期运动的参数域及颤碰转迁规律

颤碰运动是指振动系统在有限时间内与约束界面发生无限次碰撞的振幅逐渐衰减的振动，它是碰撞振动系统的一种固有运动特性。颤碰运动通常发生在一个激励周期内，它是碰撞振动系统中最重要的问题之一。在(ω,δ)参数平面上，通过分析图1所示两自由度含间隙弹性碰撞系统的力学模型，得出了系统的周期运动、颤碰及参数存在区域。

由无量纲运动微分方程(2)可知，系统的动力学特性由μm,μk,μc,ζ,f20,μk0,δ和ω八个参数决定，其中最重要的两个关键参数是间隙δ和激振频率ω。选取参数(Ⅰ)：μm=2/3,μk=5/6,μc=5/6,ζ=0.1,f20=0,μk0=0.95. 以δ∈[0,4]和ω∈[0.05,3]为参数采样范围，数值计算系统在(ω,δ)参数平面上的双参数分岔，如图2所示。弹性碰撞周期运动的参数区域用p/n及相应的颜色表示，一些未识别的周期运动和混沌运动统一用黑色区域表示。

图2 参数(Ⅰ)下系统周期运动的双参数分岔图Fig.2Diagramofdoubleparameterbifurcationofperiodicmotionsforthesystemwiththeparameters(Ⅰ)图3 低频工况下系统周期运动的双参数分岔图Fig.3Diagramofdoubleparameterbifurcationofperiodicmotionsforthesysteminlowfrequencycase图4 图3的局部放大图Fig.4ThepartialenlargementofFig.3

由图2可知，当ω>1.0时，系统存在0/1，1/1，2/2，4/4,1/2和2/4周期运动，即在中高频区出现1/1周期运动的倍周期分岔，但倍周期序列2p/2n被Saddle-node分岔或Grazing分岔打断，导致1/n(n=2, 3,…)亚谐运动的产生。在(ω,δ)参数平面的左下角区域，即δ<1.2和ω<1.0，弹性碰撞系统存在一系列p/1单周期多碰撞运动，并且随着激振频率的递减，p/1周期运动的碰撞次数p逐一增加。

为了分析p/1周期运动及其参数存在区域，数值计算系统低频工况下的(ω,δ)双参数分岔，如图3和图4所示。由图3和图4可以看出，系统在δ∈[0,1.2]和ω∈[0.05,0.95]的参数采样范围内存在完整的p/1周期运动序列。

由图3可得，当δ<1.2时，随激振频率ω的减小，小间隙系统的p/1周期运动发生Grazing分岔，碰撞次数p逐一增加，当碰撞次数p足够大时，系统呈现出Chatting-impact的动力学特征，颤碰运动增大了系统噪音和零部件磨损。随激振频率ω的减小，系统由1/1周期运动到颤碰运动的转迁规律如下：

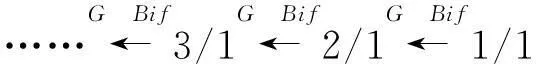
(5)

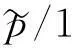
图5　δ=0.52时系统的局部分岔图 Fig.5 Local bifurcation diagrams for the system along a horizontal scan for δ=0.52

3擦边分岔及颤碰运动分析

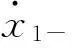
当激励频率ω∈[0.626 4,1.549 6]时，系统呈现稳定的1/1周期运动(见图6(a))，图中虚线表示位移x1=δ=0.52的弹性约束位置。当ω=0.626 4时，质量块M1以零速度接触弹性约束面，1/1周期运动Grazing分岔，碰撞次数p增加1次，形成2/1运动，1/1擦边运动相图如图6(b)所示。

当ω=0.440 5时，2/1周期运动Grazing分岔为3/1运动，2/1擦边运动相图如图7(b)所示。当ω穿越ω=0.379 59时，发生擦边分岔，3/1周期运动分岔为4/1运动，4/1周期运动Grazing分岔的临界频率为ω=0.267 94，ω=0.243 78时，5/1周期运动发生擦边分岔，6/1周期运动当ω=0.22956时擦边分岔为7/1运动，相应的擦边运动相图如图8所示。

当ω∈[0.05,0.7]时，随激振频率ω的减小，p/1周期运动发生Grazing分岔，碰撞次数p逐一增加，并且相应的参数域宽度逐渐变窄。当碰撞次数p足够大时，系统呈现出Chatting-impact的动力学特征，即在一个有限时间内(t

(a) 1/1运动,ω=0.63　　　　　(b) 1/1擦边运动,ω=0.6264　　　　　(c) 2/1运动,ω=0.6262 图6　周期运动相图 Fig.6 Phase plane portraits of periodic motions

(a) 2/1运动,ω=0.443　　　　　(b) 2/1擦边运动,ω=0.4405　　　　　(c) 3/1运动,ω=0.43 图7　周期运动相图 Fig.7 Phase plane portraits of periodic motions

图8　擦边运动相图 Fig.8 Phase plane portraits with grazing contact

图9　p/1运动时间历程图 Fig.9 Time series of p/1 motions

4擦边分岔边界上特殊运动分析

由图3和图4可以发现，在p/1周期运动发生Grazing分岔的边界上存在数个凸起的舌状区域。每个舌状区域内部均存在周期运动和混沌，如3/2，5/2，7/2，10/3，9/2，13/3等，并且其周期运动与p/1周期运动存在一定的关系。即：在p/1和(p+1)/1运动擦边分岔边界上的舌状区域内，存在(np+1)/n的周期运动序列。

图10　ω=0.352 4时系统的局部分岔图 Fig.10 Local bifurcation diagrams for the system along a vertical scan for ω=0.352 4

图11　周期运动相图 Fig.11 Phase plane portraits of periodic motions

通过以上分析和图11可知，因倍周期、Saddle-node和Grazing分岔的相互交织，在4/1和5/1周期运动之间擦边分岔边界的舌状区域内，存在9/2, 13/3, …等周期运动序列。符合在p/1和(p+1)/1运动擦边分岔边界上的舌状区域，存在完整的(np+1)/n的周期运动序列的规律。

5结论

本文以典型的两自由度含间隙弹性碰撞系统为研究对象，建立了系统的力学模型，构造了σp,σn两种Poincaré映射，分析了系统的周期运动及Grazing分岔。运用数值仿真方法，在(ω,δ)关键参数平面上详细分析了系统弹性碰撞运动的参数存在区域及颤碰运动的转迁规律。

(1)以δ∈[0,4]和ω∈[0.05,3]为参数采样范围，数值计算了系统的(ω,δ)双参数分岔，分析了间隙δ和激振频率ω两个关键参数对系统动力学特性的影响。在(ω,δ)双参数平面上分析系统的周期运动特征，可弥补单参数分岔图的不足，发现了在p/1运动擦边分岔边界上存在特定的舌状区域。

(2)当δ>1.2时系统仅有0/1和1/1等主要周期运动。当δ<1.2时，在ω>1.5中高频区开始出现1/1周期运动的倍周期分岔，但倍周期序列2p/2n被Saddle-node分岔或Grazing分岔打断，导致1/n(n=2, 3,…)亚谐运动的产生。

(3)对于p/1系列基本周期运动，在p/1和(p+1)/1运动的擦边分岔边界上的舌状区域内，存在完整的(np+1)/n的周期运动序列。

(4)在δ<1.2,ω<0.7的采样区间，系统呈现出一系列p/1周期运动。随激振频率ω的减小，系统发生Grazing分岔，碰撞次数p逐一增加，当碰撞次数p足够大时，系统呈现出Chatting-impact的动力学特征，并总结了系统由1/1周期运动到颤碰的转迁规律。

参考文献

[1]Shaw S W, Holmes P J. A periodically forced piecewise linear oscillator[J].Journal of Sound and Vibration, 1983,90(1): 129-155.

[2]Nordmark A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J]. Journal of Sound and Vibration, 1991, 145(2): 279-297.

[3]李健, 张思进. 非光滑动力系统胞映射计算方法[J]. 固体力学学报, 2007, 28(1): 93-96.

LI Jian, ZHANG Si-jin. Cell-Mapping computation method for non-smooth dynamical system[J]. Acta Mechanica Solida Sinica, 2007, 28(1): 93-96.

[4]Dankowicz H, Zhao Xiao-peng. Local analysis of co-dimension-one and co-dimension-two grazing bifurcations in impact microactuators[J]. Physica D, 2005, 202(3/4): 238-257.

[5]Nordmark A B, Kowalczyk P. A codimension-two scenario of sliding solutions in grazing-sliding bifurcations[J]. Nonlinearity, 2006, 19(1): 1-26.

[6]Mason J F, Humphries N, Piiroinen P T. Numerical analysis of codimension-one, -two and -three bifurcations in a periodically-forced impact oscillator with two discontinuity surfaces[J]. Mathematics and Computers in Simulation, 2013, 95: 98-110.

[7]Wen Gui-lin, Xu Hui-dong, Xiao Lu. Experimental investigation of a two-degree-of-freedom vibro-impact system[J]. International Journal of Bifurcation and Chaos, 2012, 22(5):1250110.

[8]吕小红, 罗冠炜. 小型振动冲击式打桩机的非线性动力学分析[J]. 工程力学, 2013, 30(11): 227-232.

LÜ Xiao-hong, LUO Guan-wei. Analysis of nonlinear dynamics of a small vibro-impact driver[J]. Engineering Mechanics, 2013, 30(11): 227-232.

[9]俞翔,朱石坚,楼京俊.基于碰撞振动的隔振系统混沌化实验研究[J].振动与冲击,2014,33(18):59-64.

YU Xiang, ZHU Shi-jian, LOU Jing-jun. Tests for chaotification method of a vibration isolation system with a vibro-impact subsystem[J]. Journal of Vibration and Shock,2014,33(18):59-64.

[10]Peterka F, Tondl A. Phenomena of subharmonic motions of oscillator with soft impacts[J]. Chaos, Solitons and Fractals, 2004, 19(5): 1283-1290.

[11]Luo G W, LÜ X H, Shi Y Q. Vibro-impact dynamics of a two-degree-of freedom periodically-forced system with a clearance: Diversity and parameter matching of periodic-impact motions[J]. International Journal of Non-Linear Mechanics, 2014, 65: 173-195.

[12]Luo G W, Zhu X F, Shi Y Q. Dynamics of a two-degree-of freedom periodically-forced system with a rigid stop: Diversity and evolution of periodic-impact motions[J]. Journal of Sound and Vibration, 2015, 334:338-362.

第一作者胡峰男，博士，副教授，硕士生导师，1979年生