基于倒谱预白化和形态学自互补Top-Hat 变换的滚动轴承故障特征提取

基于倒谱预白化和形态学自互补Top-Hat变换的滚动轴承故障特征提取

邓飞跃，唐贵基，何玉灵

(华北电力大学能源动力与机械工程学院，河北保定071003)

摘要：为了消除振动信号中离散频率分量和强背景噪声对提取滚动轴承故障特征频率的干扰，提出了一种新的基于倒谱编辑(Cepstrum Editing Procedure, CEP)预白化和形态学自互补Top-Hat变换的方法用于滚动轴承的故障特征提取。CEP能够去除故障振动信号中的周期性频率成分，剩余只包含背景噪声和碰撞损伤引起的非平稳冲击成分的白化信号，通过分析构造的形态学自互补Top-Hat变换滤波器，提出采用故障特征幅值能量比(Feature Amplitude Energy Radio，FAER)的方法自适应确定最优结构元素的尺度，预白化信号经过形态学滤波有效消除了背景噪声的干扰，提取了较为清晰的轴承故障特征频率。对实测轴承滚动体、内圈故障信号进行了分析，结果表明该方法可有效提取滚动轴承故障冲击成分并抑制噪声。

关键词：滚动轴承；倒谱编辑；信号预白化；自互补Top-Hat变换; 特征幅值能量比

中图分类号:TP206文献标志码：A

基金项目：国家自然科学基金(51378429、51308469)；中央高校基本科研业务费专项资金(2682014BR053)

收稿日期：2014-07-14修改稿收到日期：2014-12-30

基金项目：国家自然科学基金(51379091)；江苏省自然科学基金科技项目资助(BK20130516)；江苏高校优势学科建设工程资助项目(PDPA)

收稿日期：2014-04-18修改稿收到日期：2014-07-23

Fault feature extraction for rolling element bearings based on cepstrum pre-whitening and morphology self-complementary top-hat transformation

DENGFei-yue,TANGGui-ji,HEYu-ling(School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Abstract:In order to eliminate interferences from discrete frequency components and strong background noises in vibration signals to extract fault features of rolling bearings, a new method based on combining the pre-whitening technology using cepstrum editing procedure(CEP) and the morphology self-complementary Top-Hat (STH) transformation theory was presented for extracting fault features of rolling bearings. CEP could eliminate periodic frequency components in fault vibration signals, and remain pre-whitening signals containing only non-stationary impact components from collision damage and background noise. Then, through analyzing the filter constructed with the morphology self-complementary Top-Hat transformation, a novel method named fault feature amplitude energy radio (FAER) was presented to adaptively select the optimal structural element (SE) scale. The interferences of background noise in pre-whitening signals were eliminated effectively with morphological filtering, and the clearer fault feature frequencies of rolling bearings were extracted. The result showed that the proposed method is effective to extract fault impact components of roll bearings and suppress noises by analyzing vibration signals of rolling bearings with ball and inner race faults.

Key words:rolling bearing; cepstrum editing procedure; signal pre-whitening; self-complementary Top-Hat transformation; feature amplitude energy radio

滚动轴承是机械系统中应用最为广泛的部件之一，其运行状态是否良好直接影响机械系统能否安全可靠运行，因此，检测轴承故障意义重大。但是，在机械系统自身的正常振动、其他振源引起的干扰信号和白噪声等造成的强背景噪声干扰下，提取滚动轴承的故障特征较为困难，这增大了滚动轴承故障诊断的难度。

滚动轴承出现损伤性故障时，损伤点与其他元件反复碰撞产生的冲击性振动会引起轴承系统的瞬时高频共振，包络解调分析可以较为有效地分离出故障信号，但需要预先人为选定带通滤波器参数(共振中心频率和滤波带宽)才能确定最优共振频带[1]以实现包络解调，这限制了其在实际工程中的应用。基于此，国内外学者进行了广泛的研究，得出了很多研究成果[2-4]，Yan等[2]选取不同谐波小波参数对轴承故障信号进行分解，通过计算分解后各个频带的最大能量熵比来确定最优的共振频带，然后利用包络解调较为有效提取了轴承的故障特征；王冬云等[3]使用小波包理论对故障振动信号进行分解，选取能量最为集中的频段进行包络解调提取故障特征；Wang等[4]通过模拟退火法优化选择复Morlet小波中心频率和带宽，经过小波变换滤波确定最优共振频带，上述方法取得了一定的效果，但计算过程都较为复杂，而且没有考虑强背景噪声对故障特征提取的影响。Randall等[5]提出了基于倒谱编辑(Cepstrum Editing Procedure, CEP)的信号预白化方法，通过对故障振动信号进行倒谱编辑，得到分离出离散频率分量的预白化信号，不需要选取最优共振频带，通过频谱分析可直接提取轴承的故障特征，但是倒谱编辑预白化过程并不能抑制信号中的强背景噪声，使得故障特征提取效果并不理想，影响了诊断的准确性。

数学形态学(Mathematical morphology)是一种非线性空间分析方法，可以有效地提取信号的边缘轮廓以及信号的形状特征，具有很好的降噪效果，已广泛应用到机械故障信号处理中[6-7]。Santhana Raj等[8]提出使用形态学自互补Top-Hat(Self-complementary Top-Hat, STH)变换构造形态学滤波器，在提取信号冲击特征的同时能有效抑制噪声，相比形态学开-闭和闭-开运算组合滤波器，滤波器构造形式更为简单，处理速度更快。形态学结构元素是形态滤波的重要组成部分，其尺度的大小对滤波效果起着决定性作用。目前，针对结构元素尺度的选择仍是形态学中一个研究的热点。

本文结合基于CEP信号预白化和基于形态学自互补Top-Hat变换提出了一种新的轴承故障特征提取方法，利用CEP预白化处理故障信号，消除信号中离散频率分量对轴承损伤引起的非稳态冲击成分的干扰，然后通过自互补Top-Hat变换处理预白化信号，抑制白噪声等造成的强背景噪声的影响，并提出采用一种新的特征幅值能量比(Feature Amplitude Energy Radio，FAER)的方法来确定最优结构元素的尺度，最后通过频谱分析可较为清晰的提取滚动轴承的故障冲击特征。

1倒谱预白化与形态学Top-Hat变换

1.1倒谱编辑预白化

倒谱分为两种：复倒谱和实倒谱。复倒谱是复对数谱的逆傅里叶变换，表达式为：

C(τ)=F-1[ln(X(f))]

(1)

式中：X(f)是信号x(t)的傅里叶变换，为复数，表示为：

X(f)=I[x(t)]=A(f)exp(jφ(f))

(2)

因此，C(τ)保留了信号的幅值和相位信息，可以与时间信号可逆，复对数谱表示为：

ln(X(f))=ln(A(f))+jφ(f)

(3)

实倒谱是实对数谱的逆傅里叶变换，表示为：

C(τ)=F-1[ln(A(f))]

(4)

对比式(1)，实倒谱对应于相位谱为零值的复倒谱。

倒谱编辑是将实倒谱中零倒频率以外的倒谱分量置零，使所有对数谱的幅值对应同一个值，为原始信号对数幅值谱的均值，并通过与原始信号的相位谱结合生成复残余对数谱，后经过逆傅里叶变换得到剩余的预白化信号[9]。通过倒谱编辑可以去除信号频谱上的谐波和边带，剩余只包含白噪声和轴承损伤引起的非平稳冲击成分的预白化信号，振动信号的预白化过程如图1所示。需要注意的是，重构预白化信号时，因为相位信息在离散分量之间没有定义，相位谱会在全频带少数离散频率位置处出现误差，但这仅占全频带的很少部分。

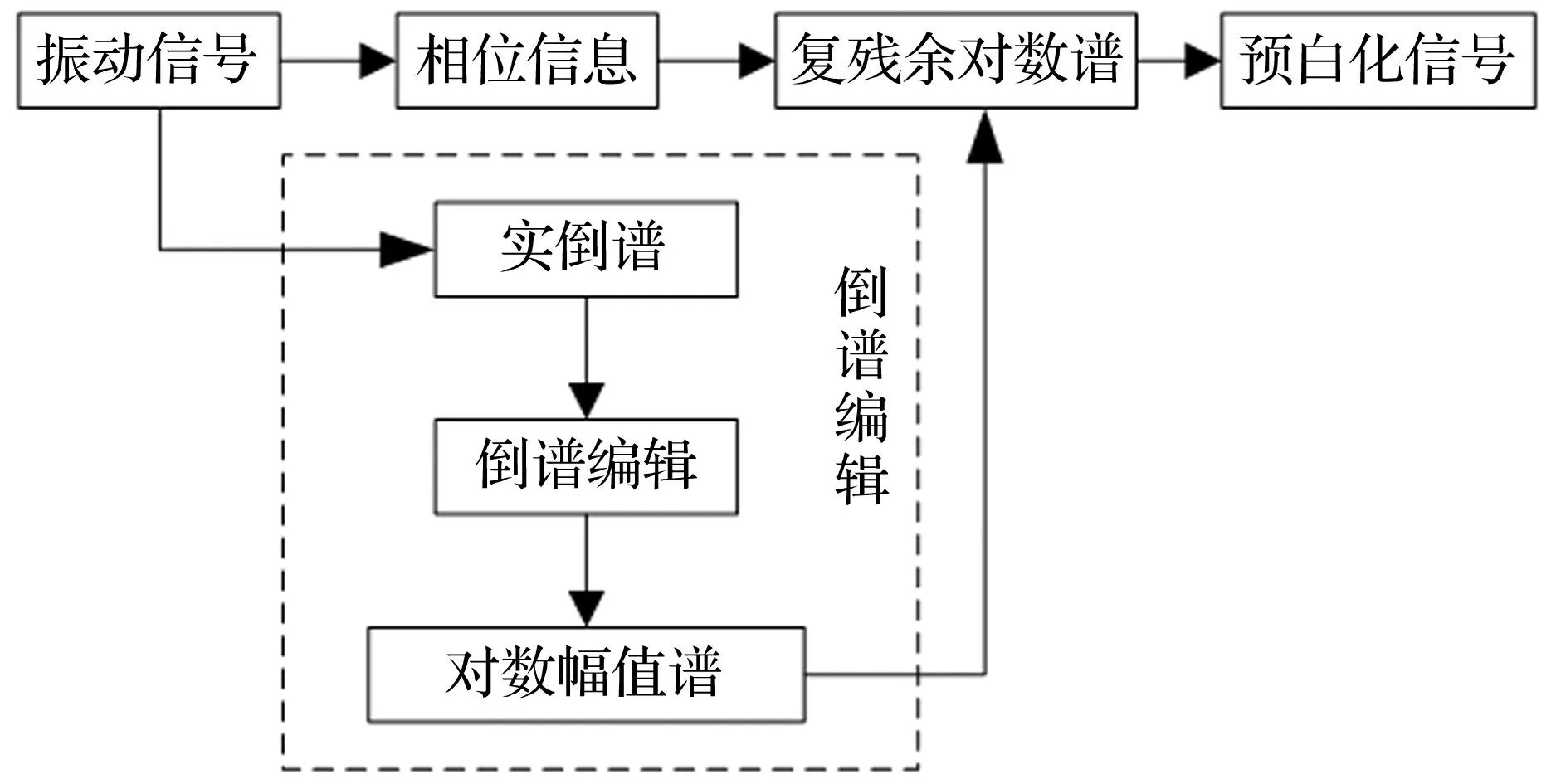
图1　基于倒谱编辑(CEP)的信号预白化处理框图 Fig.1 Signal pre-whitening process diagram based on CEP

基于CEP的信号预白化过程实质上是去除了原始振动信号中所有的离散频率分量和共振效应[10]，使预白化信号的整个频谱变成一个共振频带，因此无需再确定最优的共振频带，可直接对预白化信号进行频谱分析，通过预白化处理能够提升故障信号的冲击特性，但CEP过程并不能去除轴承故障信号中的大量背景噪声，分析结果并不理想。

1.2形态学自互补Top-Hat变换

膨胀和腐蚀是数学形态学中两个基本运算，设一维信号x(n)(n=0,1,2,…,N-1)和结构元素g(m)(m=0,1,2,…,M-1)的长度分别为N和M，且N≫M。

x(n)关于g(m)的膨胀和腐蚀分别定义为：

(x⊕g)(n)=max{x(n-m)+g(m)}

(5)

(xΘg)(n)=min{x(n+m)-g(m)}

(6)

形态学开、闭运算是由膨胀和腐蚀运算组合而成，定义分别如下：

(x°g)(n)=(xΘg⊕g)(n)

(7)

(x·g)(n)=(x⊕gΘg)(n)

(8)

形态学Top-Hat变换包含白Top-Hat(White Top-Hat, WTH)变换和黑Top-Hat(Black Top-Hat, BTH)变换，分别定义如下：

WTH(n)=x(n)-(x°g)(n)

(9)

BTH(n)=(x·g)(n)-x(n)

(10)

自互补Top-Hat(Self-complementary Top-Hat，STH)变换定义为WTH变换和BTH变换之和[8]：

STH(n)=WTH(n)+BTH(n)=

(x·g)(n)-(x∘g)(n)

(11)

开运算可以抑制信号的尖峰(正脉冲)噪声，得到的信号位于原信号下方，闭运算可以滤除信号中的陷谷(负脉冲)噪声，得到的信号位于原信号的上方。自互补Top-Hat变换等于形态学闭运算减去开运算后的差值，可以有效滤除背景噪声的干扰。

1.3特征幅值能量比

结构元素尺度决定了形态滤波过程中信号每个样本点的滤波尺度，是决定形态学滤波器性能优劣的关键因素。基于此，本文提出采用基于特征幅值能量比(FAER)的方法来确定最优的结构元素的尺度。在结构元素形状的选择上，采用了与轴承故障一维信号相似的幅值为零的直线型结构元素，结构元素基本步长为1×step，step是信号采样频率的倒数，依次增加的结构元素尺度为2×step,3×step,…,m×step，通过分析比较，本文设定结构元素最大尺度范围为m=100。

设预白化信号在结构元素某尺度时自互补Top-Hat变换后的傅里叶频谱幅值序列为X，滚动轴承故障特征频率处的幅值为X1，二倍频至五倍频的幅值分别为：X2、X3、X4和X5。

计算其能量和：

(12)

将信号前5阶倍频能量占频段总能量的比定义为特征幅值能量比，表达式如下：

η=W/W*

(13)

式中:W*为信号整个频谱段的总能量，W*=∑X2。

计算各个尺度下自互补Top-Hat变换后信号的特征幅值能量比，数值最大时表明形态学滤波后信号的故障特征最为明显，提取的故障特征也最为清晰，因此选择此时的结构元素尺度为最优结构元素尺度。

2基于倒谱预白化和形态学自互补Top-Hat故障特征提取

滚动轴承出现损伤性故障时产生的瞬态冲击成分会受到离散频率分量的干扰，经过倒谱编辑预白化处理，可得到只包含背景噪声和碰撞损伤引起的非平稳冲击成分的白化信号，通过形态学自互补Top-Hat变换能有效抑制背景噪声，提取较为清晰的故障特征。

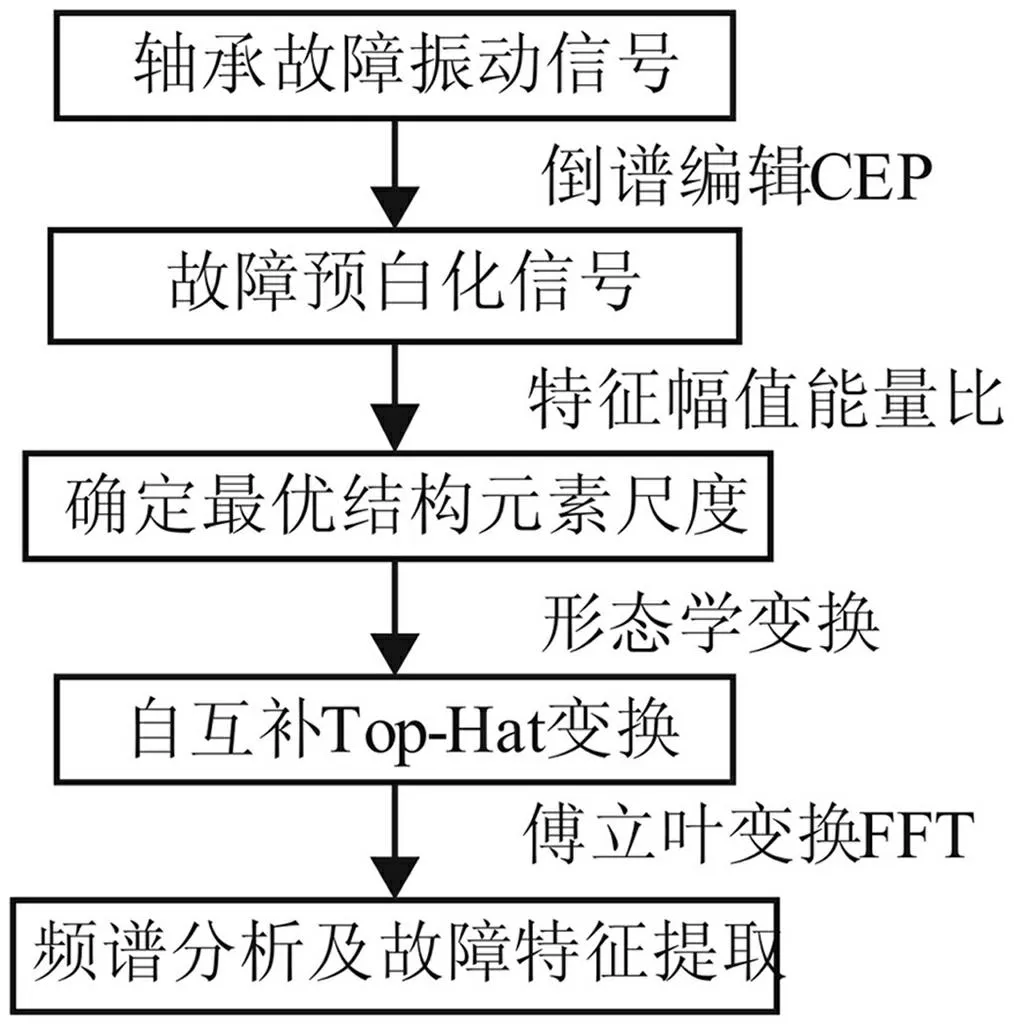
图2　算法流程图 Fig.2 Algorithm flow chart

基于倒谱预白化和形态学自互补Top-Hat变换的故障特征提取方法的算法流程如图2所示，步骤如下：

(1)倒谱分析滚动轴承的故障信号，将零倒频率以外倒谱幅值置零，结合原信号相位信息通过逆傅里叶变换得到倒谱编辑后的白化信号。

(2)计算各个尺度下信号的特征幅值能量比，通过选择最大的比值确定最优结构元素的尺度。

(3)在最优结构元素尺度下，形态学自互补Top-Hat变换处理白化信号，通过频谱分析提取滚动轴承的故障特征。

3试验验证

3.1试验平台介绍

图3　试验测试平台 Fig.3 Experiment platform

本文试验分析采用美国Case Western Reserve大学的滚动轴承试验数据，轴承型号是6205，测试平台如图3所示。故障源是轴承内圈、外圈和滚珠表面通过电火花加工的直径为0.533 4 mm(0.021 inch)，深度为0.283 14 mm(0.11 inch)的凹坑。采样频率是12 000 Hz，采样点数2 048个，轴的转速为1 772 r/min。轴承的几何参数如表1所示，计算轴承故障特征频率如表2所示。

表1　滚动轴承几何参数

表2　滚动轴承各个故障特征频率

3.2试验分析

相比滚动轴承外圈故障，滚动体和内圈的故障点位置不断变化，因此故障特征相对较为微弱，提取也更为困难。因此，本文主要分析了滚动轴承滚动体和内圈故障。

滚动体故障信号的波形和频谱如图4所示，从图4(a)中可以明显的看到故障冲击成分；从图4(b)中可知滚动体故障引起的共振频率成分主要集中在频率范围为3 000～4 000 Hz内的高频带；从图4(c)低频段频谱中可以看到150 Hz、157 Hz和187 Hz这三个频率成分较为明显，但这和滚动体故障特征频率139 Hz并不相互对应，从频谱中并没有提取出滚动体故障特征信息。经过倒谱编辑(CEP)处理后，预白化信号的时域波形和频谱如图5所示，相比图4中的频谱，可以较为明显看到140 Hz和276 Hz频率成分，这和滚动体故障特征频率和二倍频非常接近，故障振动信号经过CEP预白化处理后，不需要确定最优共振频带，可直接进行频谱分析提取故障特征。

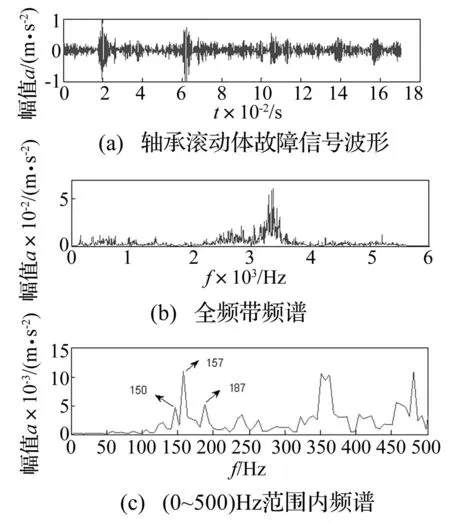
图4　轴承滚动体故障的信号波形和频谱 Fig.4 Signal waveform and spectrum of bearing ball fault

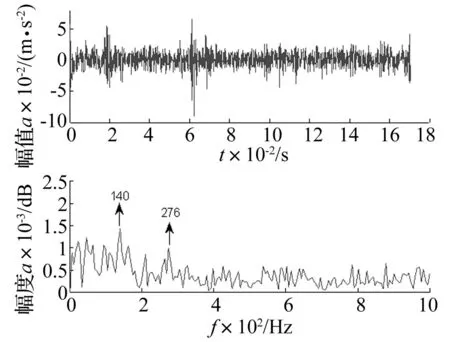
图5　滚动体故障的预白化信号和频谱 Fig.5 Pre-whitening signal and spectrum of bearing ball fault

因为原始轴承故障信号比较理想，背景噪声非常微弱，信号经CEP预白化后通过频谱分析就可以得出故障特征频率。但在实际工程中，滚动轴承通常在较为恶劣的条件下工作，通过传感器获得的故障振动信号往往包含有大量的背景噪声[11-12]，而CEP过程不能去除信号中的背景噪声，提取故障特征并不理想。为更好验证本文所提方法的有效性，使得分析的轴承故障信号更接近生产实际，本文在原始信号基础上添加了方差为0.4的高斯白噪声，图6为滚动体故障信号添加噪声后经过CEP预白化后的波形和频谱，从频谱图中可知由于噪声的干扰，滚动体故障特征已完全被掩盖，无法识别。

图6　滚动体故障添加噪声后的预白化信号和频谱 Fig.6 Pre-whitening signal waveform and spectrum of bearing ball fault with noise

图7　滚动体故障噪声信号时的特征幅值能量比曲线 Fig7. The curve of FAER of bearing ball fault signal with noise

图8　滚动体故障预白化信号 自互补Top-Hat变换后的波形和频谱 Fig.8 Waveform and spectrum of pre-whitening signal STH transform of bearing ball fault

采用自互补Top-Hat变换处理添加噪声的预白化信号，计算不同结构元素尺度时的特征幅值能量比，结果如图7所示。峰值位于A点，结构元素尺度为21时，最大特征幅值能量比是0.119，确定最优结构元素尺度为21，经自互补Top-Hat变换后信号的波形和频谱如图8所示，从频谱图中，可以清楚看到与滚动体故障特征频率非常接近的140 Hz频率成分，深入分析频谱，可以提取出与滚动体故障特征非常接近的二倍频280 Hz频率成分和轴承保持架故障特征频率12 Hz，因此可以判断是轴承滚动体出现故障，与未经过处理的图6相比，形态学自互补Top-Hat变换较为有效的抑制了预白化信号中的强背景噪声。

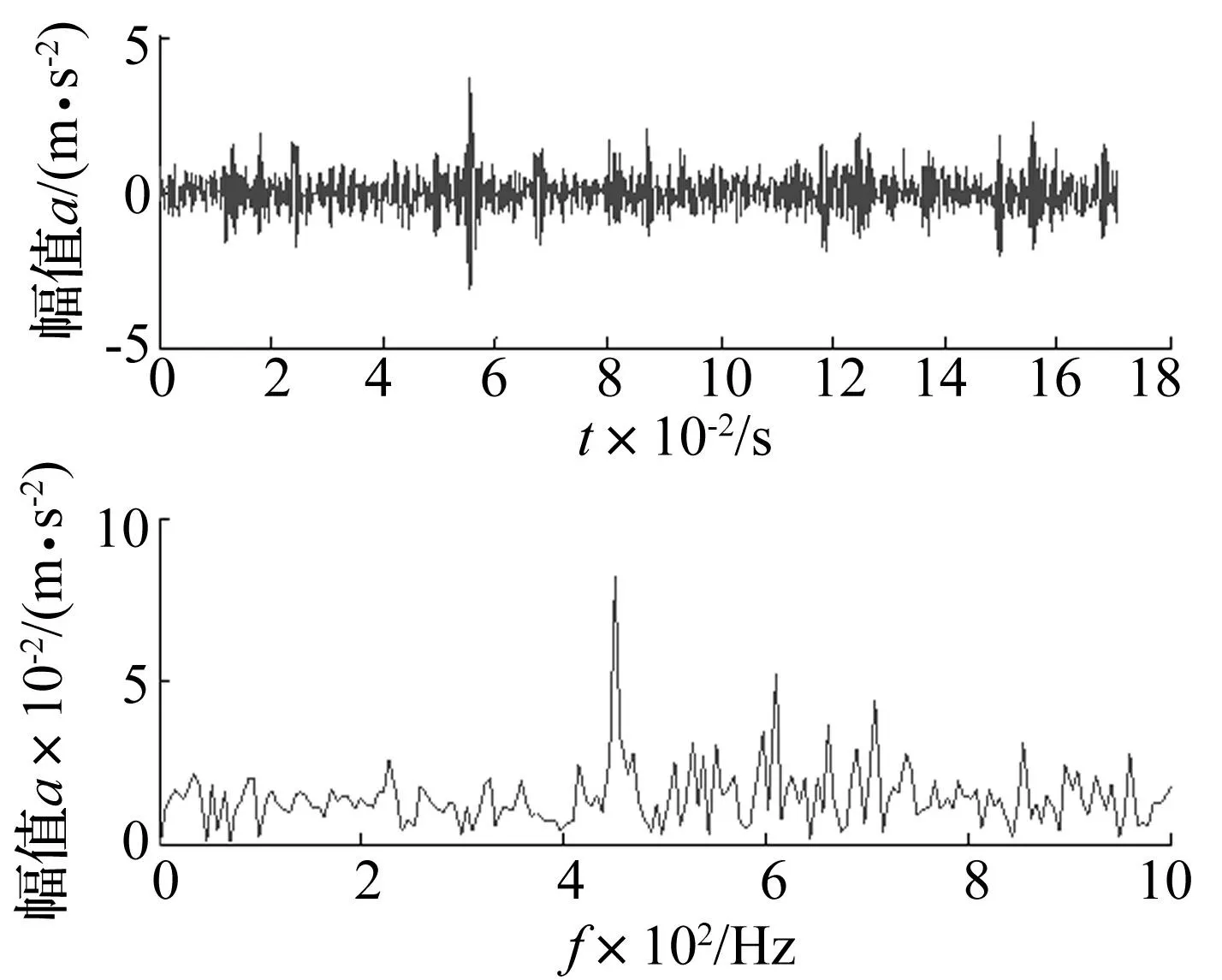
图9　添加噪声后轴承内圈故障信号的时域波形和频谱 Fig.9 Vibration signal waveform and spectrum of bearing inner race fault with noise

图10　添加噪声后内圈故障预白化信号的波形和频谱 Fig.10 Waveform and spectrum of pre-whitening of bearing inner race fault with noise

滚动轴承内圈故障信号添加方差为0.4的高斯白噪声后的波形和频谱如图9所示，由于强背景噪声的干扰，无法识别频谱图的细节。该信号经过CEP预白化后的信号波形和频谱如图10所示，从频谱图中可以分辨出内圈故障特征频率及二倍频成分160 Hz和322 Hz，但由于杂频成分较多，故障特征提取效果并不理想。计算结构元素各个尺度下自互补Top-Hat变换后的特征幅值能量比，结果如图11所示，顶峰为B点，结构元素尺度为17时，最大特征幅值能量比是0.144 8，确定最优结构元素尺度为17，自互补Top-Hat变换后的波形和频谱如图12所示，从频谱图中较为清楚的看到159 Hz、321 Hz和480 Hz频率成分，这与内圈故障特征频率、二倍频、三倍频成分非常接近，因此可以判断是轴承内圈出现故障，相比图10，本文方法有效抑制了信号中强背景噪声，实现了对内圈故障特征的提取。

图11　内圈故障噪声信号时的特征幅值能量比曲线 Fig.11 The curve of FAER of bearing inner race fault signal with noise

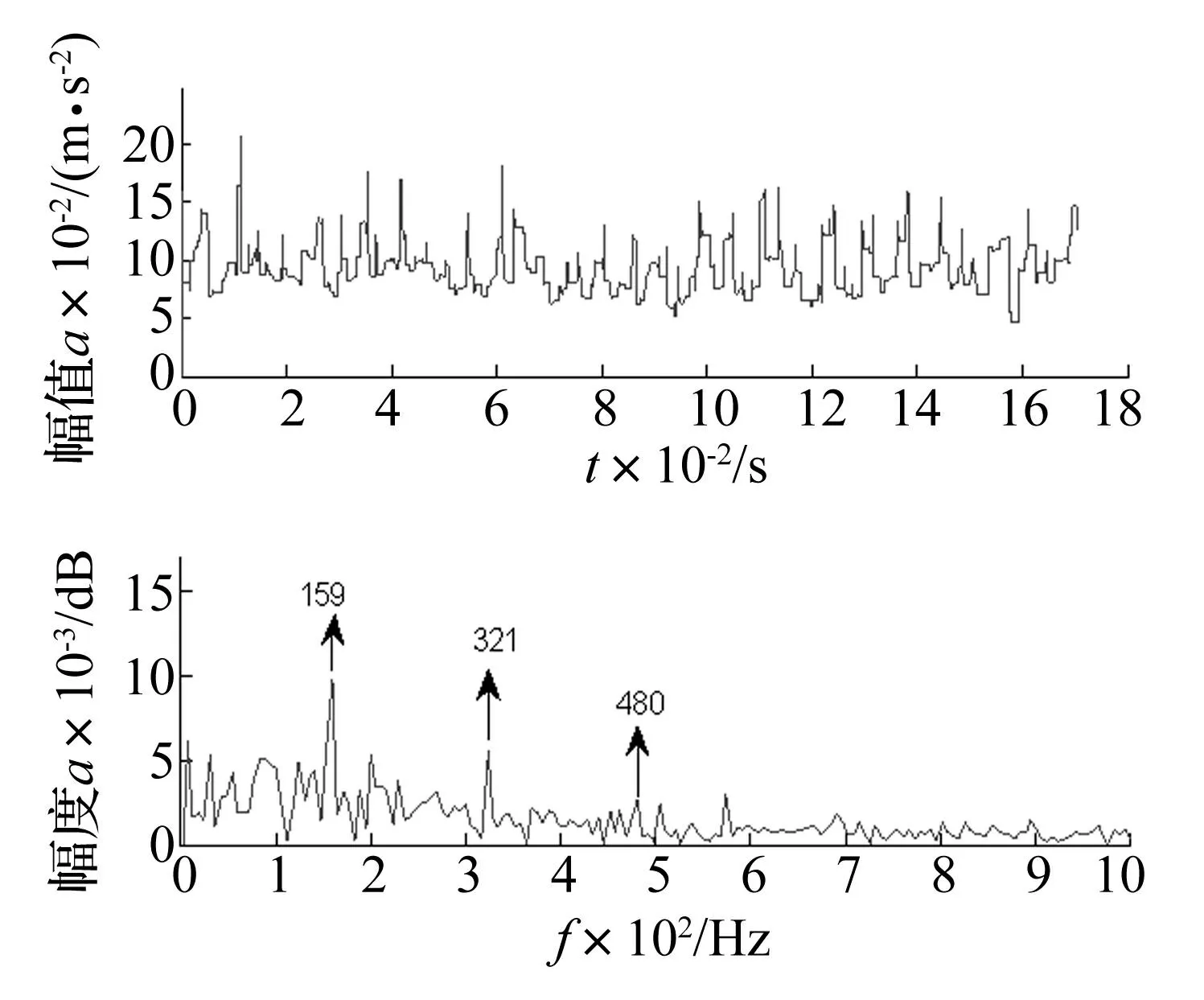
图12　内圈故障预白化信号 自互补Top-Hat变换后的时域波形和频谱 Fig.12 Waveform and spectrum of pre-whitening signal STH transform of bearing inner race fault

4结论

倒谱编辑预白化方法能够去除故障信号中离散频率分量对滚动轴承损伤引起的非稳态冲击成分的干扰，但不能抑制信号中强背景噪声的干扰，因此直接通过频谱分析提取轴承故障特征的效果并不理想。通过自互补Top-Hat变换构造的形态学滤波器能有效抑制预白化信号中强背景噪声的干扰，基于此，本文采用CEP预白化方法和自互补Top-Hat变换方法提取滚动轴承故障特征，实现了两种方法较为理想的结合，并通过实验分析，证实本文方法的有效性。

参考文献

[1]王宏超, 陈进, 董广明, 等. 基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J]. 振动与冲击, 2013, 32(1):35-37.

WANG Hong-chao, CHEN Jin, DONG Guang-ming, et al.Application of resonance demodulation in rolling bearing fault feature extraction based on fast computation of kurtogram[J]. Journal of Vibration and Shock, 2013, 32(1):35-37.

[2]Yan Ru-qiang, Gao R X. Harmonic wavelet-based data filtering for enhanced machine defect identification[J]. Journal of Sound and Vibration, 2010, 329(15):3203-3217.

[3]王冬云, 张文志. 基于小波包变换的滚动轴承故障诊断[J]. 中国机械工程, 2012. 23(3):295-298.

WANG Dong-yun, ZHANG Wen-zhi. Fault diagnosis study of ball bearing based on wavelet packet transform[J].China Mechanical Engineering, 2012, 23(3):295-298.

[4]WANG Dong, GUO Wei, WANG Xiao-juan. A joint sparse wavelet coefficient extraction and adaptive noise reduction method in recovery of weak bearing fault features from a multi-component signal mixture[J]. Applied Soft Computing, 2013, 13(10):4097-4104.

[5]Randall R B，Sawalhi N. A new method for separating discrete components from a signal[J]. Journal of Sound & Vibration，2011，45(5)：6-9.

[6]Shen Chang-qing, He Qing-bo, Kong Fan-rang, et al.A fast and adaptive varying-scale morphological analysis method for rolling element bearing fault diagnosis[J]. Journal of Mechanical Engineering Science,2012,227(6):1362-1370.

[7]Dong Ya-bin, Liao Ming-fu, Zhang Xiao-long, et al.Faults diagnosis of rolling element bearings based on modified morphological method[J]. Mechanical Systems and Signal Processing, 2011, 25(4):1276-1286.

[8]Santhana Raj A,Murali N. Early classification of bearing faults using morphological operators and fuzzy inference[J]. IEEE Transactions on Industrial Electronics, 2013. 60(2):567-574.

[9]Borghesani P, Pennacchi P, Randall R B, et al. Application of cepstrum pre-whitening for the diagnosis of bearing faults under variable speed conditions[J]. Mechanical Systems and Signal Processing, 2013, 36(2):370-384.

[10]张晓飞，胡茑庆，胡雷. 基于倒谱预白化和随机共振的轴承故障增强检测[J]. 机械工程学报,2012,48(23):84-89.

ZHANG Xiao-fei, HU Niao-qing, HU Lei. Enhanced detection of bearing faults based on signal cepstrum pre-whitening and stochastic resonance[J]. Journal of Mechanical Engineering, 2012. 48(23):84-89.

[11]李兵，张培林，刘东升,等. 基于自适应多尺度形态梯度变换的滚动轴承故障特征提取[J]. 振动与冲击, 2011, 30(10):104-108.

LI Bing，ZHANG Pei-lin, LIU Dong-sheng, et al. Feature extraction for roller bearing fault diagnosis based on adaptive multi-scale morphological gradient transformation[J]. Journal of Vibration and Shock，2011, 30(10):104-108.

[12]张超, 陈建军. 随机共振消噪和局域均值分解在轴承故障诊断中的应用[J]. 中国机械工程, 2013,24(2):215-219.

ZHANG Chao, CHEN Jian-jun. Application of stochastic resonance and LMD to bearing fault diagnosis[J].China Mechanical Engineering, 2013,24(2):215-219.

第一作者张迅男，博士，讲师，1985年7月生

通信作者李小珍男，博士，教授，1970年1月生

第一作者付强男，博士，副研究员，1975年11月生