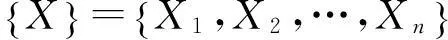采用广义 Pareto 分布进行车辆荷载效应极值估计的研究

采用广义Pareto分布进行车辆荷载效应极值估计的研究

冯海月1，伊廷华1,2，陈斌3

(1. 大连理工大学土木工程学院，辽宁大连116023；2. 同济大学土木工程防灾国家重点实验室，上海200092；3.浙江工业大学建筑工程学院，杭州310003)

摘要：为了解决车辆荷载效应数据间的相关性问题并能够充分利用样本数据，提出了一种改进的独立风暴法。首先提出了一种三次类阈值法进行数据的初步分析来获得阈值；然后考虑到简支梁桥的车辆荷载效应主要受单辆重车影响，提出了改进的独立风暴法进行独立同分布样本数据的提取；最后采用广义Pareto分布进行车辆荷载效应极值估计；利用该方法，对动态称重系统记录的国内某大桥实测数据进行了车辆荷载效应极值估计，并与超越阈值法、独立风暴法进行了对比分析，结果表明：在较短评估期(T<20年)内，三种方法均可以较好地预测荷载效应极值；而在中长评估期内，改进的独立风暴法预测值较高，预测结果偏于安全。

关键词：车辆荷载效应；广义Pareto分布；阈值；独立风暴法；动态称重系统

中图分类号:TU312.1文献标志码：A

基金项目：国家自然科学基金(10632040, 11302058)

收稿日期：2014-06-13修改稿收到日期：2014-07-16

基金项目：汽车仿真与控制国家重点实验室开放基金(20121117)；中央高校基本科研业务费专项资金(长安大学基础研究支持计划专项基金CHD2012JC021)

收稿日期：2014-07-09修改稿收到日期：2014-09-03

Extreme estimation for vehicle load effect based on generalized Pareto distribution

FENGHai-yue1,YITing-hua1,2,CHENBin3(1. School of Civil Engineering, Dalian University of Technology, Dalian 116023, China;2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;3. College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310003, China)

Abstract:In order to solve data correlation problems for vehicle load effect and make full use of data samples, the modified method of independent storms (MMIS) was proposed. Firstly, a triple-class threshold method was proposed to obtain the threshold with the primary data analysis. Then, considering that the vehicle load effect of simply supported beam bridges was mainly affected by a single heavy vehicle, the MMIS was adopted to extract the independent and identically distributed (IID) sample data. Finally, the extreme vehicle load effect was estimated with the generalized Pareto distribution. In the end, the estimation of the extreme vehicle load effect was performed for the measured data of a bridge recorded with the weighinmotion (WIM). The results were compared with those of the peak-over-threshold method and those of the method of independent storms. The results showed that within the shorter estimation period (T<20 years), all the three methods can be used to better predict the extreme load effect; while within the middle or longer estimation period, the estimation of the modified method of independent storms is higher and safer.

Key words:vehicle load effect; generalized Pareto distribution; threshold; method of independent storms; weighinmotion (WIM)

车辆荷载是影响桥梁结构安全性和耐久性的主要因素之一。近年来，随着我国交通货运量呈现爆发式的增长，重车和超重车已逐渐成为最重要的运输工具之一。因此，针对桥梁所处位置的交通状况，建立精确的车辆荷载效应模型，具有重要的现实意义。车辆荷载效应是一个随机过程，它受车重、轴重、车间距、轴距、多车同时作用以及车速等多因素耦合作用的影响。精确的车辆荷载效应模型不但能够对交通车辆的限载提供基础依据，而且能够为桥梁安全评估、寿命预测及养护维修提供有力的支持。

动态称重系统(Weigh In Motion，WIM)是一组安装的传感器和含有软件的电子仪器，用以测量动态轮胎力和车辆通过时间并提供计算轮重、轴重、总重(如车速、轴距等)的数据[1-2]。由于它可以准确获取实际车流数据，因此通过这些数据可以进行车辆荷载效应的计算，进而利用极值理论来预测未来荷载效应的情况[3]。传统基于极值的方法均是基于加载事件服从独立同分布这一基本假设[4]，而实际的车辆荷载效应属于平稳时间序列，数据之间具有一定的相关性，因此简单地将荷载效应作为独立同分布序列并不十分合理。Cook[5]通过分析一段时间内的风暴最大值，提出了独立风暴理论(Method of Independent Storms，MIS)，并采用Gumbel分布进行拟合，得到了不同评估期的荷载极值。Bhattacharya[6]认为平稳荷载为点过程序列，他通过分析相关独立性，并结合阈值超过数的分簇研究，提出了极值指标的计算方法，得到了平稳时间序列分布函数。Naess等[7]基于极值理论是渐进分布，在实际应用时无法判断在多大程度上适用于实际数据的问题，提出了针对Gumbel 分布的最大值分布模型。Mazas等[8]针对超越阈值法(Peak Over Threshold，POT)中阈值的合理选择问题，提出了一种双阈值方法，并进行了不同评估期荷载取值研究。李春前[9]提出了类BM离散法，得到近似独立荷载数据，采用广义Pareto分布(Generalized Pareto Distribution，GPD)来拟合车辆荷载效应的尾部分布，认为一天荷载效应值只代表一天最大值截口分布，从而得到了更加贴近实际的车辆荷载效应概率模型。Wang等[10]针对数据的非独立性，提出将原始数据序列在足够大的时间间隔中提取出来，得到渐进独立数据，并结合POT分簇算法得到最优阈值，然后采用GPD分布进行拟合，得到了短期荷载极值分布。

本文采用GPD模型对车辆荷载效应尾部值进行了估计研究，提出了一种三次类阈值法进行数据的初步选择，并针对数据间的相关性问题，提出了一种改进的独立风暴法(Modified Method of Independent Storms，MMIS)；最后利用WIM记录的某桥一个月实际车流数据，对不同设计基准期的车辆荷载效应极值进行了预测，并与POT模型的方法进行对比，得到了一些有益的结论。

1极值理论和GPD模型

1.1极值理论

根据极值理论[11]，设独立同分布的随机样本{X}={X1，X2…Xn}服从某个未知的分布函数F(x)。假设Mn=max{Xi}，则存在数列an>0和bn∈R，使得当n→∞时，概率Pr{(Mn-bn)/an

这三种分布代表了三种不同的极值行为，可以用统一的形式进行表示：

(2)

式中：μ,k∈R，σ>0；μ是位置参数；σ为尺度参数；k为形状参数。H(x)称为广义极值分布，当k=0时，H(x)为极值Ⅰ型，分布的尾部呈指数状；k>0时，H(x)为极值Ⅱ型，分布的尾部较长；k<0时，H(x)为极值Ⅲ型，分布具有有限的上端点。

对于式(2)，当有足够大的阈值u，且X>u时，有超出量Y=X-u样本服从GPD分布：

(3)

1.2车辆荷载效应的极值理论

概率密度函数可以分为低尾、中间、和高尾三部分[12]。由于传统的单峰或者多峰分布拟合方法可以满足车辆荷载效应分布中低尾和中间部分的精度要求，因此本文主要进行高尾部分的研究。

根据GPD理论，当u值选定时，样本变量X的累积概率分布为：

(4)

2独立样本数据的获取

传统计算车辆荷载效应极值的方法是由WIM系统获得实际车辆的相关信息，然后根据科学计算软件来模拟产生荷载效应，并通过一定的时间间隔将效应值划分为若干段，通过提取每段的最大值作为分析的样本。若选择的时间间隔足够长，则认为可以采用极值理论。通常选择的时间间隔为一天，然后假设一天的荷载效应最大值为全年最大值，然后应用极值理论进行不同基准期的荷载效应最大值评估。这种方法计算简单，应用较为普遍。但是一天的荷载效应只使用一个最大值，其他数据则不考虑会造成数据的极大浪费；或者选择某个阈值，提取大于这个阈值的所有样本数据，并用GPD方法进行拟合，从而得到车辆荷载效应分布函数。阈值的选择会直接影响到结果的准确性。过大的阈值会使超出量太少，造成估计量的方差较大；而过小的阈值，则会使得估计量成为有偏估计[11]。

2.1三次类阈值法

本文提出的三次类阈值法的基本思想是剔除荷载效应样本值中的低尾和中间部分，从而得到MMIS法分析所需的样本，具体步骤为：

(1)根据样本数据经验分布函数，得到类阈值u1。类阈值u1应取在样本经验分布函数的中间部分，这样不仅可以将原始数据中低尾的部分剔除掉，而且还可以减少类阈值u2的选择循环次数，从而节省类阈值的选择时间。提取大于u1的样本{Y}={Y1,Y2，…，YN}，这里N为原始样本中大于u1的个数。

(2)由平均超出函数法，初步得到一个类阈值u2。类阈值u2的值宜取样本经验分布函数的中间部分，这样可以保证得到的数据样本不会丢失风暴值。平均超出函数[13]是类阈值u2的线性函数，其表达式为：

(5)

式中：μ,k∈R，σ>0；μ,σ,k分别对应极值分布中的位置参数、尺度参数和形状参数。

对于样本{Y}={Y1,Y2…YN}，平均超出函数可由经验平均超出函数(Empirical mean excess function，EMEF)en(u2)来估计，表达式为：

(6)

(3)根据原始样本{X}得到累计分布函数值为0.99所对应的样本值，此值即为类阈值u3。在这里将类阈值u3作为三次类阈值法的阈值选择上限。

(4)分别将类阈值u2和u3作为MIS法的阈值进行分析。如果MIS法得到的两个类阈值所对应的独立风暴个数相差一个量级，则重新进行类阈值u2的选择，直到前后选择的类阈值u2所对应的MIS样本数相差不超过一个量级。这样选择类阈值u2的原因是，MIS法对阈值的稳定性较好，阈值适当的提高或减小对MIS分析样本不会产生太大的影响[14]。

2.2MMIS法

MIS法首先需要确定出阈值u。Cook[5]将阈值点称为平静点，两个平静点之间为独立风暴。即若是连续数据超过阈值u，就将其看作为是一个独立风暴；将每个独立风暴的最大值作为独立样本，忽略掉该数据段中较小的其它值。

由于MIS法在获取数据样本时，仅关注两个连续阈值之间的最大值，并不考虑连续阈值区间次大值是否大于邻近区间的最大值，从而会造成数据的浪费；且同时考虑到简支梁桥实际车辆荷载效应最大值主要是由重车控制这一特点，本文提出了一种MMIS法。具体步骤为：

(1)由三次类阈值法得到阈值u。

(2)将连续超过阈值u的车辆荷载效应作为一个独立的风暴段，记录风暴段中的最大值和次大值的位置。假设其中的两个风暴段为{Zi}={Zi-j,Zi-j+1，…，Zi}和{Zk}={Zk-j,Zk-j+1，…，Zk}；令Mi=max{Zi}，Mk=max{Zk}，Mk-1为序列{Zk}中次最大值。

(3)比较Mk-1和Mi。如果Mk-1>Mi，而且Mk-1和Mi之间的距离大于某个固定值s时，则将Mk-1加入最后选取的独立风暴样本。s取为根据实测车辆荷载数据统计特性得到的单辆重车长度。独立风暴值的分布函数为：

(7)

(4)假设R年中有m个独立风暴样本，年平均风暴发生概率为r，且r=m/R。假设一年内车辆运行情况变化不会太大，则设计基准期T年发生的风暴总数概率分布为：

(8)

3工程算例

由于实际的车辆类型多样，各生产厂家生产的车辆轴距也不尽相同，直接进行实测车辆的分析计算比较困难。根据WIM记录的某桥一个月实际车流数据，并参考计算桥梁疲劳时的车辆荷载类型分类，将车辆类型分为七类，各类型车辆所占总数量的比例及车辆简图见表1。各类型车辆轴重所占车重的比例以及轴距直接在车辆简图中表示。由实测的车辆荷载统计数据通过蒙特卡洛法模拟生成随机车辆，并根据影响线加载[9]分别得到车辆在经过30 ～ 60 m桥时的跨中弯矩值。

表1　车辆分类及各车型比例统计

以50 m跨径简支梁桥分析为例。由随机车辆产生的简支梁跨中弯矩值经验分布函数见图1。由不同阈值得到的平均超出函数见图2。由经验分布函数选定类阈值u1为6 000 kN·m，但根据平均超出函数图得到的初步类阈值u2为10 000 kN·m，故初步选定类阈值为u2。累计分布函数值为0.99所对应的类阈值u3为11 046 kN·m。初步类阈值u2对应的MIS法样本个数为140个，类阈值u3对应的MIS样本数为48个。因为样本个数相差很多，故重新选择类阈值u2为10 500 kN·m，此时类阈值u2所对应的样本数为85个。再次选择类阈值u2为10 600 kN·m，对应的MIS样本个数为80个。因为前后选择的类阈值u2所对应的MIS样本个数相差较小，故选择阈值为10 500 kN·m所对应的样本为分析样本。

图1　简支梁桥50 m跨中弯矩频率直方图 Fig.1 Bending moment frequency histograms of 50 m midspan of simply supported beam bridge

图2　经验平均超出函数图 Fig.2 Empirical mean excess function

简支梁桥最大车辆荷载效应一般由重车控制。根据WIM记录的车辆荷载统计特点，四轴车车重较大，而且相比五、六轴车出现的概率较大，因此本文选取四轴车所对应的桥梁影响长度为近似s值，s取为10 m。由MIS方法得到的独立样本数据共85个。GPD分布拟合参数为k=-0.129 7。由于k<0是个截尾分布，参考李植淮等[16]的建议，将样本数据顺序排列，取k=0，利用式(3)可得到σ值为847.531。由MMIS法得样本数据116个。GPD分布拟合参数为k=-0.225 64。取k=0，得到σ为1 000.815。则MIS法最大值截口分布为：

x>1.05×104

(9)

MMIS法得到的最大值截口分布为：

x>1.05×104

(10)

由POT方法得到的最大值截口分布为：

x>1.05×104

(11)

其它跨径桥梁类阈值、MIS法和MMIS法样本个数见表2。

表2　简支梁桥各跨径样本个数

采用规范[15]给出的一天荷载效应最大值分布代表一年最大值分布，取分位值满足FT(x)=0.95的x作为弯矩设计值，计算上述三种不同方法弯矩设计值与设计基准值之间的关系如图3所示。

图3　三种分析方法的弯矩设计值与基准期之间的关系 Fig.3 Bending moment v.s. service life of three methods

由图3可知：①三种方法都可以反映出荷载效应极值随基准期增加而增大的基本变化规律。②POT方法由于数据具有一定的相关性，其结果明显偏小；而MIS方法虽然选择的数据近似独立，但是由于选择的数据样本较少，其结果也偏小，但较POT估计结果准确。③随着桥梁跨径的增加，POT法和MIS法评估得到的车辆荷载效应极值相差越来越小。造成这种现象的原因是，随着桥梁跨径的增加，车辆荷载效应最大值不再主要是由单辆重车控制引起，而是要考虑多车同时作用的影响。④这三种方法都可以较好地反映样本的尾部变化规律，在较短的周期(T<20年)，三种方法估计结果相差不多。因此，在进行旧桥评估时，三种方法都可使用，因为旧桥的剩余寿命一般少于20年。⑤在中长期(T>20年)荷载效应极值估计时，POT和MIS法估计结果明显偏低。因此，在对新建桥梁或拟建桥梁荷载效应计算时，本文提出的MMIS法估计结果更为保守，也偏于安全。

4结论

由于车辆荷载效应样本是平稳时间序列，具有一定的相关性。为了解决数据间的相关性问题，本文对MIS法进行了改进，提出了MMIS法。同时提出了一种三次类阈值法，通过该阈值法来得到MMIS法的样本。并以WIM记录的某桥一个月实际样本数据进行了分析，得到了以下结论：

(1)本文提出的三次类阈值法，有效地克服了POT方法中阈值需要精确选择的问题。根据样本经验分布函数进行类阈值u1的选择；通过经验平均超出函数法进行类阈值u2的初步选择，并结合MIS法具有对阈值的稳定性较好的特点进行类阈值u2的最终确定；并将类阈值u3作为阈值选择上限，取样本累积分布函数值为0.99所对应的值。该方法程序实现简单，收敛效率较高。

(2)结合简支梁桥车辆荷载效应主要受单辆重车影响的特点，对MIS法不能充分利用原始样本数据的缺陷进行了改进，提出了MMIS法。由于MMIS法的分析样本不仅相互独立，而且相比MIS法数据利用更加完全，因此得到的分析结果也更为可靠。

(3)通过对某桥WIM记录的一个月实际车流量分析得到的车辆荷载效应值进行分析，得到以下结果：①若评估期较短，在对旧桥承载力评估或者确定旧桥加固方案时，理论上三种方法的模拟结果相近，都可以使用。但是相比POT方法阈值的选择、MIS方法中的平静点确定，本文提出的用三次类阈值法进行样本数据的选择更为简单，而且也较为准确。②若评估期较

长，在对拟建桥梁或新建桥梁服役期间进行最大荷载效应估计时，POT方法和MIS方法可能会低估车辆荷载效应，隐藏着车辆设计荷载偏小的危险；而利用MMIS方法估计未来设计期限内的荷载效应值则较为保守，偏于安全。

参考文献

[1]Sivakumar B, Ghosn M, Moses F. Protocols for collecting and using traffic data in bridge design[M]. Washington: Transportation Research Board, 2011.

[2]Kozikowski M. WIM based live load model for bridge reliability[D]. Nebraska: Dissertation to the University of Nebraska, 2009.

[3]Nowak A S. WIM based lived load model for bridges[R]. Florida: Published in Transportation Board, 2011.

[4]Galambos J. The asymptotic theory of extreme order statistics[M]. Malabar: Krieger, 1987.

[5]Cook N J. Towards better estimation of extreme winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 9(3): 295-323.

[6]Bhattacharya B. The extremal index and the maximum of a dependent stationary pulse load process observed above a high threshold[J]. Structural Safety, 2008, 30(1): 34-48.

[8]Mazas F, Hamm L. A multi-distribution approach to POT methods for determining extreme wave heights[J]. Coastal Engineering, 2011, 58(5): 385-394.

[9]李春前. 基于GPD模型的车辆荷载效应极值估计[D]. 北京: 清华大学,2012.

[10]Wang Y, Xia Y, Liu X. Establishing robust short-term distributions of load extremes of offshore wind turbines[J]. Renewable Energy, 2013, 57: 606-619.

[11]史道济. 实用极值统计方法[M]. 天津: 天津科学技术出版社, 2006.

[12]Caers J, Maes M A. Identifying tails, bounds and end-points of random variables[J]. Structural Safety, 1998, 20(1): 1-23.

[13]赵旭. 广义Pareto分布的统计推断[D]. 北京: 北京工业大学, 2012.

[14]An Y, Pandey M D. A comparison of methods of extreme wind speed estimation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(7): 535-545.

[15]中华人民共和国住房和城乡建设部. 工程结构可靠性设计统一标准(GB 50153-2008) [S]. 北京: 中国建筑工业出版社.

[16]李植淮,李春前,孙健康,等.基于GPD模型的车辆荷载效应极值估计[J].工程力学,2012,29(增刊1):166-171.

LI Zhi-huai, LI Chun-qian, SUN Jian-kang, et al. Estimation of extreme vehicle load effect based on GPD model[J]. Engineering Mechanics, 2012,29(Sup1): 166-171.

第一作者符毅强男，硕士生，1991年生

通信作者陈予恕男，教授，中国工程院院士，1931年生

邮箱：yschen@hit.edu.cn

第一作者张平男，博士，讲师，1977年生

通信作者马建男，博士，教授，博士生导师，1957年生