一个新三阶动力系统及其仿真
一个新三阶动力系统及其仿真
尹社会1,张勇1,舒永录2
(1.河南工业职业技术学院,河南 南阳 473000;2.重庆大学 数学与统计学院,重庆 401331)
摘要:构建了一个新的三阶动力系统,利用Matlab软件和理论分析,得到了混沌系统在一定参数组合和初值下的Lyapunov指数和Lyapunov维数,也探讨了全局动力学行为和局部动力学行为,研究结果表示新混沌系统不同于现有的三维混沌系统.
关键词:动力系统;Lyapunov指数;动力学行为
DOI:10.13877/j.cnki.cn22-1284.2015.10.007
收稿日期:2015-04-22
基金项目:国家自然科学
作者简介:尹社会,河南沈丘人,讲师.
中图分类号:O357.1;N945文献标志码:A
著名的Lorenz系统作为一个简单的三维自治蝴蝶状混沌吸引子是研究混沌现象的典型范例[1-2].随后,又有新的混沌吸引子不断被发现,Chen系统和Lü系统相继被提出[3-4],统一混沌系统也被陈关荣和吕金虎提出并研究[5].此后,国内外不少学者相继提出新的混沌或超混沌系统[6-17],新系统的提出促进了人们对混沌现象的深入研究和认识,提高了混沌理论在工程上的应用能力.本文根据新混沌系统的必要条件,通过添加含有绝对值的非线性项构造了一类新的混沌系统,并进行了动力学方面的研究,得到了一定参数组合和初值条件下的Lyapunov指数以及Lyapunov维数,在全局动力学特性方面包括对称性、耗散性、吸引子的存在性等进行了数学分析.
1数学模型及其吸引子的存在性
构造一个三维类Lorenz混沌系统的方程为

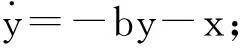
(1)
其中,(x,y,z)∈R3为状态变量;a,b,c,d为系统实参数.当a=8,b=-0.05,c=2,d=4时,系统相空间的时间平均散度为
-a-1-b-d=-19.8<0
(2)
可知,系统为一个耗散非线性动力系统,其轨线随着时间不断演化到一个不变的吸引子集合中,其初值取(2,1,0),系统(1)的吸引子轨线的相图,如图1所示.

图1 吸引子相图
2混沌吸引子的动力学特性分析
由数值计算可得,系统的3个Lyapunov指数分别为:λ1=0.362,λ2=0,λ3=-2.323,其中有1
个大于0,1个等于0,1个小于0,且3个Lyapunov指数之和小于0,说明系统处于混沌状态.进一步通过Kaplan-Yorke猜想可以得到其分形维数为
(3)
可见系统具有分数维数,进一步验证了系统处于混沌状态.
对混沌系统的吸引子分析,其空间结构十分复杂,轨线无穷延伸、压缩和折叠,其轨线在特定的吸引域内具有遍历性.
混沌系统的Poincaré截面上是两个近似闭合轨线的独立分布和沿几条曲线弧分布着一些具有分形结构的密集点,如图2所示,图中给出了x=0(y-z)平面上的Poincaré映射,进一步说明了系统处于混沌态.

图2 Poincaré映射
3系统的平衡点分析


4系统参数的影响
非线性动力系统的动力学行为主要由系统参数决定,随着系统参数的变化,系统表现出极限环(周期轨或拟周期轨)和奇怪吸引子等不同的非线性行为,即出现Hopf分叉和混沌现象.不同参数组合下的Lyapunov指数谱图显示,当固定其余参数只有一个参数发生变化时,系统表现出不同的动力学行为,如图3所示.参数a具有很宽的调节空间,并且随着其数值的增加,逐渐表现出恒定Lyapunov指数的行为,这一点对于构建恒Lyapunov指数混沌系统或超混沌系统具有重要的借鉴意义.

图3 系统单参数变化的Lyapunov指数谱图
对于特殊的参数组合,可以得到不同的动力学行为,借助相图可以明显地进一步表现出这一特性,如图4所示,其中图4(a)为参数组合a=4,b=-0.05,c=2,d=4下的相图,图4(b)为参数组合a=4,b=0.2,c=2,d=4下的相图,图4(c)为参数组合a=4,b=-0.05,c=5,d=4下的相图,图4(d)为参数组合a=4,b=-0.05,c=2,d=8下的相图.从图4(c)可以发现另一个有趣的现象,这里的拟周期轨线和其余几组参数组合下的周期轨线或拟周期轨线明显不同,不仅结构稍微复杂,而且沿z轴方向大范围展开,这一点说明了即便处于相似的动力学状态,其吸引子的范围是有很大差别的.因此关于参数组合对动力系统的动力学特性的影响的研究是一件非常有意义的事情.这里的相图没有显示比较典型的周期轨线或拟周期轨线,主要是由于保留了初值附近的计算数据,以便和混沌吸引子的相图相比较具有一致性.

图4 几种参数组合下的吸引子的相图
5结论
本文研究了一种三维自治动力系统,对系统的基本动力学行为进行了研究,包括Poincaré截面,Lyapunov指数和Lyapunov指数谱图等.参数组合下的动力学特性分析表明,该系统具有丰富的动力学行为,系统在参数变化时的动力学行为的演变呈现出周期、复杂周期(拟周期)、混沌运动,这些结论为系统的电子振荡电路的实现和通信工程设计等应用提供了理论依据.
参考文献:
[1]Lorenz E N. Deterministic non-periods flows[J]. Journal of Atmosphere Science, 1963, 20(2):130-141.
[2]尹社会,张勇,张付臣,等.基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J].东北师大学报,2014,46(1):42-47.
[3]Guan rong CHEN, Tetsushi UETA. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos, 1999,9(7):1465-1466.
[4]Jin hu Lü, Guan rong Chen. A new chaotic attractor coined[J]. International Journal of Bifurcation and Chaos, 2002, 12(3): 659-661.
[5]Jin hu Lü, Guan rong Chen, Dai zhan CHENG, et al. Bridge the gap between the Lorenz system and the Chen system[J].International Journal of Bifurcation and Chaos, 2002,12(12):2917-2926.
[6]Chong xin Liu, Tao Liu, Ling Liu. A new chaotic attractor Chaos[J]. Chaos, Solitons and Fractals, 2004, 22: 1031-1038.
[7]Chong xin Liu, Ling Liu, Tao Liu. A novel three-dimensional autonomous chaos system[J]. Chaos, Solitons and Fractals, 2009, 39: 1950-1958.
[8]李春来,禹思敏,罗晓曙.一个新的混沌系统的构建与实现[J].物理学报,2012,61(11): 252-260.
[9]尹社会,张勇,徐鹏飞.一个三维混沌系统的动力学行为及反馈同步[J].江西科学,2013,31(6):717-721.
[10]J C Sprott. A dunamical system with a strange attractor and invariant tori[J].Physics Letters A, 2014,378:1361-1363.
[11]唐良瑞,李静,樊冰,等.新三维混沌系统及其电路仿真[J].物理学报,2009,58(2):785-793.
[12]章秀君,吴志强,方正.超混沌系统的构造方法研究[J].计算机工程与应用,2014,50(2):92-98.
[13]HU Yu, MIN Le-quan, ZHEN Ping. Existence of heteroclinic orbits in a novel three-order dynamical system[J]. Chinese Physics B, 2013, 22(11):110.
[14]尹社会,曹辉.一个4维超混沌类Lorenz系统动力学分析[J].广西物理,2014,35(4):14-19.
[15]尹社会,张勇,皮小力.自治混沌系统的动力学行为及计算机仿真[J].广西物理,2015, 36(1): 32-37.
[16]高智中,韩新风,章毛连.一个新的四维超混沌系统及其电路仿真[J].东北师大学报,2012,44(1):77-83.
[17]高智中.一个新超混沌系统及其线性反馈同步[J].中山大学学报,2012,51(6):30-34.
(责任编辑:陈衍峰)
A Novel Three-order Dynamical System and It's Simulation
YIN She-hui1, ZHANG Yong1, SHU Yong-lu2
(1.HenanPolytechnicInstitute,Nanyang,Henan473000,China;
2.CollegeofmathematicsandStatistics,ChongqingUniversity,Chongqing401331,China)
Abstract:In this paper, a novel three-order dynamical system is proposed. The calculation of Lyapunov exponents and Lyapunov dimension with initial conditions and the combination of parameters is obtained. Furthermore, the global dynamical behavior and local dynamical behavior is investigated by theoretical analysis and simulative analysis based on Matlab software. The results show that the novel chaotic system is different from existing three dimensional chaotic systems in published literature now.
Key words:dynamical system;Lyapunov exponent;dynamical behavior

