一类带跳倒向重随机微分方程解的轨道唯一性

一类带跳倒向重随机微分方程解的轨道唯一性

杨叙1，李硕2

(1.北方民族大学 数学与信息科学学院，宁夏 银川 750021；2.昌吉学院 数学系，新疆 昌吉 831100)

摘要:建立一类带跳倒向重随机微分方程解的轨道唯一性，此工作是 He 等给出结果的一般化．

关键词:带跳倒向重随机微分方程；轨道唯一性；Gauss 白噪声；Poisson 随机测度

DOI:10.13877/j.cnki.cn22-1284.2015.10.010

收稿日期：2015-04-20

基金项目：国家自然科学

作者简介：杨叙,宁夏银川人,博士,讲师.

通讯作者：李硕,甘肃天水人,副教授．

中图分类号：O212文献标志码：A

倒向重随机微分方程最初是在文献[1]中建立的，文献[2-5] 中建立了随机偏微分方程和倒向重随机微分方程的关系,并通过对倒向重随机微分方程的研究,得到了随机偏微分方程解的性质.特别地,文献[2]中建立了一类带跳倒向重随机微分方程解的轨道唯一性准则.

WT([0,t]×A)=W([T-t,T]×A),

0≤t≤T,A∈B(E).

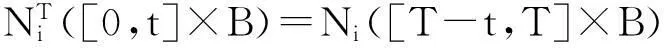
0≤t≤T,B∈B(Ui).

{ξs:s∈[0,T]}

({ξs(u):s∈[0,T],u∈E},{ξs(u):s∈[0,T],

u∈F},{ξs(u):s∈[0,T],u∈Ui})

组成的空间:

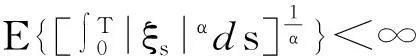
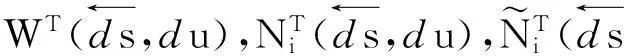
考虑以下带跳倒向重随机微分方程

(1)

本文的主要目的是研究方程(1)解的轨道唯一性，先给出以下条件.

条件1 (i)函数x→β(x)是R上的连续函数并且可以分解为β=β1-β2，其中β2为连续非递减函数．

(ii)存在一个R上的不减的凹函数x→γ(x)，使得∫0+γ(x)dx=∞且

∫U1|g1(x,u)-g1(y,u)|μ1(du)+

|β1(x)-β1(y)|≤γ(|x-y|),x,y∈R.

(iii)对每个u∈U0,x→g0(x,u)是不减函数，且

∫E|σ(x,u)-σ(y,u)|2π(du)+

∫U0|g0(x,u)-g0(y,u)|2u0(du)≤

C|x-y|,x,y∈R.

定理1 假定条件 1成立，且

{(Y1(t),Z1(t),ζ1(t,u)):0≤t≤T,u∈F},

{(Y2(t),Z2(t),ζ2(t,u)):0≤t≤T,u∈F}

为(1)式满足Y1(T)=Y2(T)的解．则对于每个0≤t≤T，都有P{Y1(t)=Y2(t)}=1成立且

(2)

注:在条件 1 中，若β1≡0，γ(x)=x，则定理 2为文献[2]中定理 2.3 的结果．

证明令α(t)=Y1(t)-Y2(t)，β1(s)=β1(Y1(s))-β1(Y2(s)),β2(s)=β2(Y1(s))-β2(Y2(s)),Z(t)=Z1(t)-Z2(t),ζ(t,u)=ζ1(t,u)-ζ2(t,u),γi(t,u)=gi(Y1(t),u)-gi(Y2(t),u) ,其中i=0,1．由(1)式可知，

(3)

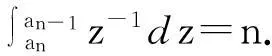
φn(α(s))-φn(α(s))γ0(s,u)]μ0(du)-

φn(α(s))-φn(α(s))ζ(s,u)]v(dz)

(4)

其中,Mn(t)是一个期望为零的随机过程．注意到第三项和第五项是非正的．注意到，当z≥0时，φ'(z)≥0，当z≤0时，φ'(z)≤0，于是由条件 1 知(4)式中的第2项也是非正的.由函数序列{φn}的性质及条件1易得到，当n→∞时，

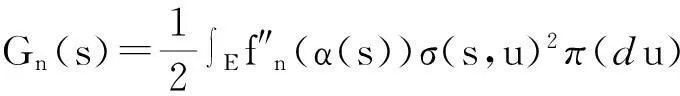
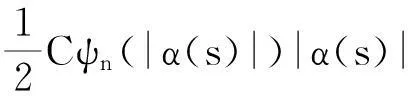
由条件1及文献[6]中定理 3.2 的讨论，证明当n→∞时，

ψn(s)=∫U0[φn(α(s)+γ0(s,u))-φn(α(s))-

φn(α(s))γ0(s,u)]μ0(du)→0

此时，由(4) 式和 Fatou 引理知

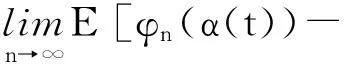
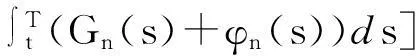
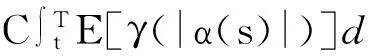
由函数x→γ(x)的凹性及Jensen不等式可得到

这蕴含着E[|α(t)|]=0，因此P{Y1(t)=Y2(t)=1}．利用(3)式知

对上式两边平方再取期望可得

这就证明了(2)．

参考文献：

[1]Pardoux E, Peng S. Backward doubly stochastic differential equations and systems of quasilimear SPDEs[J]. Probab. Theory Related Fields, 1994, 98: 209-227．

[2]He H，Li Z, Yang X. Stochastic equations of super-Lévy processes with general branching mechanism[J]. Stochastic Process. Appl., 2014, 124: 1519-1565．

[3]Li Z, Liu H, Xiong J, et al. Some properties of the generalized Fleming-Viot processes[J]. Stochastic Process. Appl., 2012, 123: 4129-4155．

[4]Xiong J. SBM as the unique strong solution to an SPDE[J]. Ann. Probab., 2013, 41: 1030-1054．

[5]杨叙.非Lipschitz系数的带跳随机偏微分方程的轨道唯一性[J].北京师范大学学报,2014,50:221-228．

[6]Fu Z, Li Z. Stochastic equations of non-negative processes with jumps[J]. Stochastic Process Appl., 2010, 120: 306-330．

(责任编辑:陈衍峰)

Pathwise Uniqueness for A Class Backward Doubly SDEs with Jumps

YANG Xu1,LI Shuo2

(1.SchoolofMathematicsandInformationScience,BeifangUniversityofNationalities，Yinchuan,

Ningxia750021,China;2.DepartmentofMathematics,ChangjiUniversity,Changji,Xinjiang831100,China)

Abstract:In this paper,the pathwise uniqueness for a class of backward doubly stochastic differential equations with jumps is established．It generalizes the recent work of Section 2 in He et al．

Key words:Backward doubly stochastic equation with jumps；pathwise uniqueness；Gaussian white noise；Poisson random measure