四分裂导线尾流驰振数值模拟研究

四分裂导线尾流驰振数值模拟研究

严波1,蔡萌琦1,吕欣2,周林抒1

(1.重庆大学工程力学系，重庆400044； 2.重庆大学土木工程学院，重庆400044)

摘要：利用风洞试验测量四分裂导线的空气动力系数，得到各子导线的空气动力系数随风攻角的变化曲线，表明尾流干扰对处于上风子导线尾流区的子导线的气动特性影响明显。给出利用ABAQUS有限元软件模拟分裂导线尾流驰振过程的方法，进而针对典型四分裂导线线路段，模拟得到包括整档舞动和次档距振动的尾流驰振现象，分析了整档舞动和次档距振动的特征，以及间隔棒不同布置方式和风速对尾流驰振的影响。

关键词：四分裂导线；空气动力特性；尾流驰振；数值模拟

中图分类号:TM753； O39文献标志码：A

Numerical simulation on wake galloping of quad bundle conductor

YANBo1,CAIMeng-qi1,LÜXin2,ZHOULin-shu1(1. Department of Engineering Mechanics, Chongqing University, Chongqing 400044, China; 2.College of Civil Engineering, Chongqing University, Chongqing 400044, China)

Abstract:Aerodynamic coefficients varying with the angle of attack were measured in wind tunnel tests. It is shown that the aerodynamic characteristics of a sub-conductor locating at the wake zone of another sub-conductor are apparently affected by the wake interference. The wake galloping including full span galloping and sub-span oscillation of a typical quad bundle conductor line was numerically simulated by means of ABAQUS software. The effects of mounted spacers with non-uniform and uniform arrangement schemes at different wind speeds on the wake galloping characteristics of the line were analyzed.

Key words:quad bundle conductor; aerodynamic characteristics; wake galloping; numerical simulation

双圆柱尾流干扰研究表明，上风圆柱的尾流区会形成两个不稳定的区域，一个近距失稳区和一个远距失稳区。前者约位于圆柱直径的1.5倍～6倍距离范围，后者约位于圆柱直径的10倍～25倍距离范围[1-2]。分裂导线子导线的间距正好使下风子导线处于上风子导线的远距失稳区中，可能引起分裂导线的气弹性失稳，诱发尾流驰振[3]。分裂导线的尾流驰振主要表现为次档距振动，并可能伴有整档舞动。尾流驰振发生时通常持续时间较长，易于引起导线、线夹、绝缘串和间隔棒等的疲劳破坏，对线路的安全运行形成严重威胁。

Tokoro等[2]利用风洞测试了双索在一定间距范围时的气动特性，并讨论了尾流驰振现象。陈政清等[4-5]针对桥梁吊杆和拉索的尾流驰振问题进行了研究。关于分裂导线的尾流驰振问题在20世纪70年代即在国际上引起关注，但公开报道的研究成果较少。Price[6]利用风洞试验测量了一种表面光滑的导线和两种绞股导线在两种湍流度、不同Reynolds数下下风子导线的升力系数和阻力系数与其在尾流区中的位置之间的关系。Wardlaw等[7]对分裂导线的气动特性和尾流驰振问题进行了较全面的研究。他们利用风洞试验测量了二分裂、四分裂、六分裂和八分裂导线的气动特性，研究了子导线在尾流区中的具体位置、导线表面光洁度、自由来流的湍流度和Reynolds数等对其气动特性的影响。进而在风洞中实施了尾流驰振节段模型试验，并利用理论简化模型分析了分裂导线的次档距振动。此外，对分裂导线绕流问题和气动特性的数值模拟研究近年也引起了重视。Braun等[8]研究了模拟多分裂导线气动力和气弹性的二维流动数值模拟方法，其模型中考虑了流体的可压缩、粘性、流体和固体之间的耦合作用，并利用该二维模型模拟分析了双分裂、三分裂和四分裂导线的尾流驰振动力失稳问题。

然而，已有的工作重点研究处于上风子导线尾流区的子导线的气动特性，即阻力和升力系数随子导线所处位置等的变化规律。尚未见到多分裂导线各子导线的气动系数在全攻角范围内的变化规律的研究，也未见采用三维数值模型模拟研究分裂导线尾流驰振的成果。本文利用风洞试验测量四分裂绞股裸导线的气动系数随风攻角的变化规律，进而采用有限元方法模拟研究典型线路段的尾流驰振过程，对进一步研究抑制尾流驰振的方法具有重要意义。

1空气动力系数风洞试验

分裂导线中处于上风子导线尾流中的子导线除了受到阻力作用外，还会受到升力的作用，这是引起尾流驰振的根本原因。因而有必要利用风洞试验获得分裂导线各子导线的气动系数随风攻角的变化规律。

以四分裂导线4XLG-400/50为研究对象。子导线的直径为27.6 mm，相邻子导线之间的间距为450 mm。已有的研究表明，绞股导线的气动特性与光滑圆杆的气动特性差别明显[6-7]，因此，导线模型在铝管表面缠绕胶线以模拟绞股导线的外形。四分裂导线模型为节段模型，测量有效长度为700 mm。模型两端连接有圆形端板，以确保来流的二维特性，上、下端板均采用较轻的木板制作而成。试验模型如图1所示。

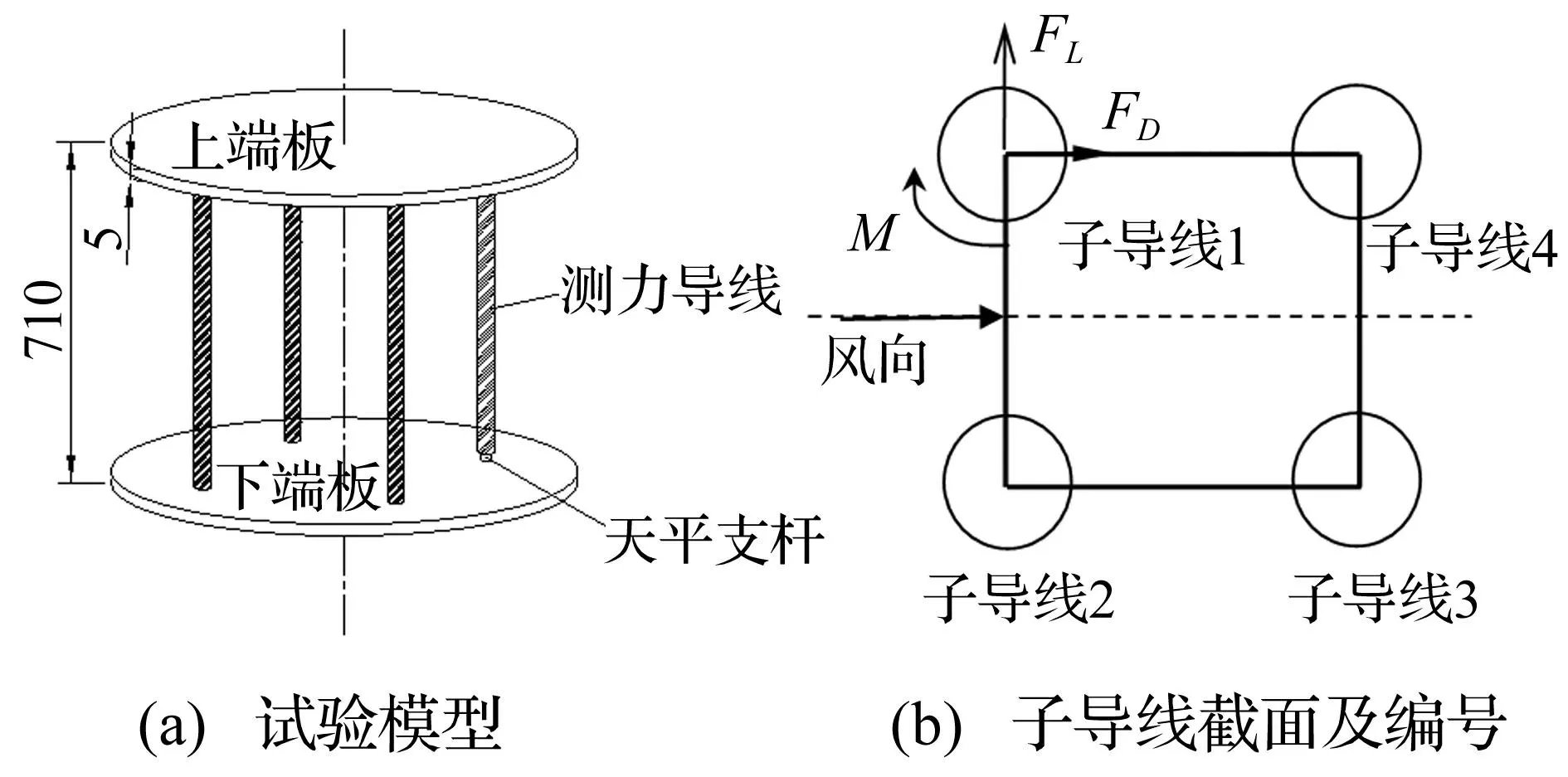
图1　四分裂导线试验模型 Fig.1 Test model of quad bundle conductor

风洞试验在中国空气动力研究与发展中心1.4×1.4 m低速风洞中完成。该风洞为直流式低速风洞，截面形状为切角矩形，试验段长2.8 m，风速范围为0～65 m/s。使用TG0151A和TG0151B天平测量导线模型的阻力、升力、扭矩三分力。导线测力试验数据采集系统选用的是PXI系统。分裂导线模型安装在装置中间，两杆式天平分别安装在对称的两根导线模型内部，测量导线模型的阻力、升力、扭矩三分力。安装天平的两根导线模型的下端与下端板之间留有约1～2mm的缝隙，以保证试验过程中模型、下端板之间无接触，天平支杆直接从上端板穿出，与支撑装置的固定架固接。其余两根导线模型两端与上、下端板固接。下端板与固定在风洞下转盘中心的圆柱形支撑杆固接。试验时，通过同步转动风洞上下转盘改变风攻角。风洞试验模型、导线模型以及测力天平如图2所示。

本试验中不考虑来流湍流度的影响，即测量稳定风下的气动参数。在-180°~180°风攻角范围测量每一根子导线的气动力，风攻角增量为5°。

子导线的阻力系数、升力系数和扭矩系数定义如下

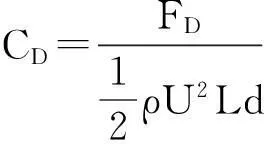
(1)

式中:FD,FL,M分别为导线模型所受的阻力、升力和扭矩；ρ为试验气温下的空气密度；U为风速；L为导线模型的有效长度；d为导线的直径。

图2　四分裂导线风洞试验模型 Fig.2 Wind tunnel test model of quad bundle conductor

图3所示为风速12m/s时，测得的四分裂导线各子导线的气动系数随攻角的变化曲线。从图中可以看出，由于尾流的影响，四根子导线的空气动力系数存在较明显的差异。当子导线处于上风子导线的尾流区时，作用于其上的阻力会下降，同时会受到升力的作用，而在整个风攻角范围内，扭矩作用非常小，可以忽略不计。

图3　四分裂导线空气动力系数 随风攻角的变化(风速：12 m/s) Fig.3 Aerodynamic coefifcient of quad bundle comductor (wind speed:12 m/s)

2分裂导线尾流驰振有限元模拟方法

输电导线属于柔性结构，其运动过程中的变形属于典型的几何非线性问题。在此不考虑导线运动过程中杆塔变形的影响，模型中仅考虑分裂导线和间隔棒。在ABAQUS软件中，可将空间杆单元的材料性质设置为不可压缩，得到模拟导线的索单元。间隔棒相对于导线具有较大的刚度，可简化为正方形框，用空间梁单元模拟。分裂导线有限元建模方法详见文献[9]。

由于作用于裸导线上的扭矩非常小，不予考虑。因而作用于子导线上的气动载荷仅包括阻力和升力。由式(1)可知，作用于各子导线上的气动载荷为

(2)

式中，导线运动过程中的风攻角可由下式确定

(3)

值得一提的是，这里所述方法适用于任何分裂导线尾流驰振过程的模拟。

3分裂导线尾流驰振数值模拟

3.1典型线路段及有限元模型

以档距为200 m的线路段为研究对象。导线型号为4XLGJ-400/50，直径为27.6 mm，其它参数如表1中所列。每个间隔棒的质量为4.8 kg。线路的初始水平张力为29.988 kN。

表1　导线参数

线路模型如图4所示。线路上安装4个间隔棒，采用非等间距布置和等间距布置两种方案。非等间距布置方案按现行输电线路设计规程[11]确定，第1个间隔棒距离左端30 m，其余依次增加50 m、42.5 m、50 m。等间距布置时，各间隔棒之间相距40 m。

图4　档距200 m线路模型 Fig.4 Quad bundle conductor line model with span length of 200 m

导线的阻尼一般采用Rayleigh阻尼模型[12-13]

C=αM+βK

式中:C，M和K分别为阻尼矩阵、质量矩阵和刚度矩阵，α和β为Rayleigh阻尼系数，可由导线的固有频率和阻尼比确定。根据文献[10-11]，导线的阻尼系数β几乎为零，裸导线的阻尼比取1.0%，则利用导线的面内一阶频率0.476 Hz(见表2)，可计算得到α=0.06。

按第3节中所述方法，用索单元离散各子导线，将间隔棒简化为正方形框，用梁单元模拟。单元收敛性检查表明，模拟导线的单元长度取0.5 m时可以满足精度要求。

3.2整档模态和次档距局部模态

尾流驰振发生时，除了次档距振动外，还可能发生整档舞动[7]。整档舞动特征与整档的模态和固有频率有关，而次档距振动特征则与次档距的局部模态有关。

利用ABAQUS软件分析得到两种间隔棒布置方式下该线路段整档在垂直和水平方向的低阶模态和固有频率，如表2所列。可见，间隔棒的布置方式对线路整档模态的影响非常小。

表2　线路段整档模态及其固有频率

此外，间隔棒非等间距布置时，在频率1.419 Hz～1.780 Hz范围内出现密集的固有频率，对应的模态均为次档距内子导线的单半波形式。如图5所示为在间隔棒非等间距布置时，其中几个典型的次档距局部模态。间隔棒等间距布置时对应的局部模态与非等间距布置方式类似，固有频率也很接近。

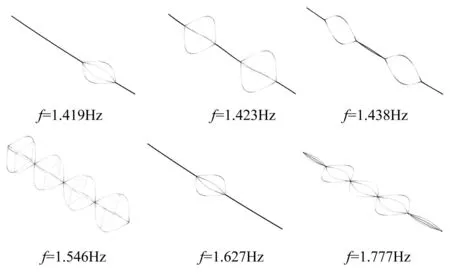
图5　间隔棒非等间距布置时几个典型次档距局部模态 Fig.5 Local sub-span modes of quad bundle conductor line with unequally arranged spacers

3.3线路整档舞动

利用第3节所述方法对线路在稳定风作用下的驰振过程进行数值模拟。图6所示为在间隔棒非等间距布置时，风速为12 m/s的情况下两典型时刻的运动状态。可见，该线路发生了整档舞动和次档距振荡。

结合下节的位移响应频谱分析可知，其垂直和水平方向位移频谱在0.45 Hz处有一峰值，接近于垂直方向单半波模态对应的固有频率0.476 Hz(见表2)，因此，其整档舞动模式为垂直向的单半波。另外，图7给出了该情况下子导线1中点的位移时程，可见，整档舞动达到稳定时，该点的运动轨迹为椭圆。由于分裂导线各子导线之间的尾流干扰，引发了导线整档驰振现象[7]。

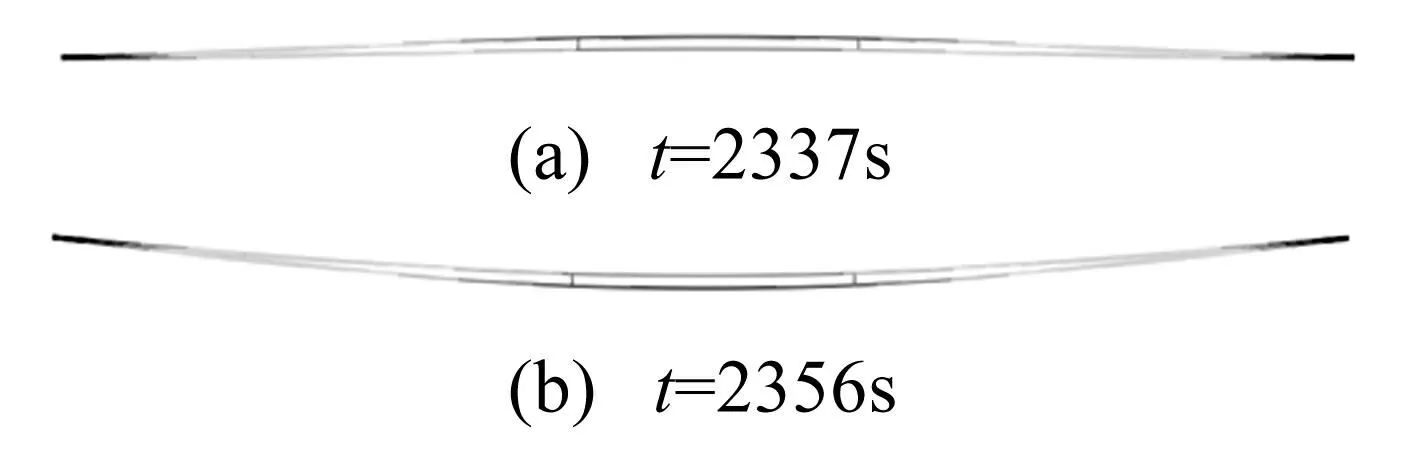
图6　间隔棒非等间距布置时典型时刻 导线的运动状态(风速：12 m/s) Fig.6 Moving status of conductor lines with unequally arranged spacers at typical times (wind speed:12m/s)

为研究风速对尾流驰振的影响，模拟计算了8 m/s、12 m/s、16 m/s和20 m/s等四种风速下的驰振响应。表3给出了两种间隔棒布置方案下各子导线中点的驰振幅值。可见，各子导线的振幅存在一定的差异，处于迎风侧的子导线1和2的垂直振动幅值大于处于背风侧的子导线3和4的垂直振动幅值，这是由于尾流干扰导致作用于各子导线上的气动载荷不同所致。另外，间隔棒等间距布置情况下，导线的驰振幅值比非等间距布置方式的大，说明间隔棒采用均匀布置方式对于尾流驰振的防治不利。最后，由不同风速下导线的位移时程响应结果还可知，达到稳定驰振状态所需的时间随风速的增大而减少，与文献[7]的结论一致。

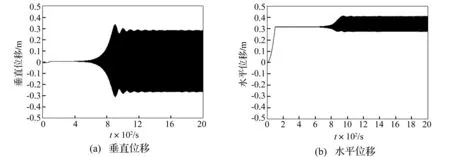
图7　间隔棒非等间距布置时子导线1中点位移时程(风速：12 m/s) Fig.7 Time histories of displacements at mid-span of sub-conductor 1 of conductor line with unequally arranged spacers(wind speed:12 m/s)

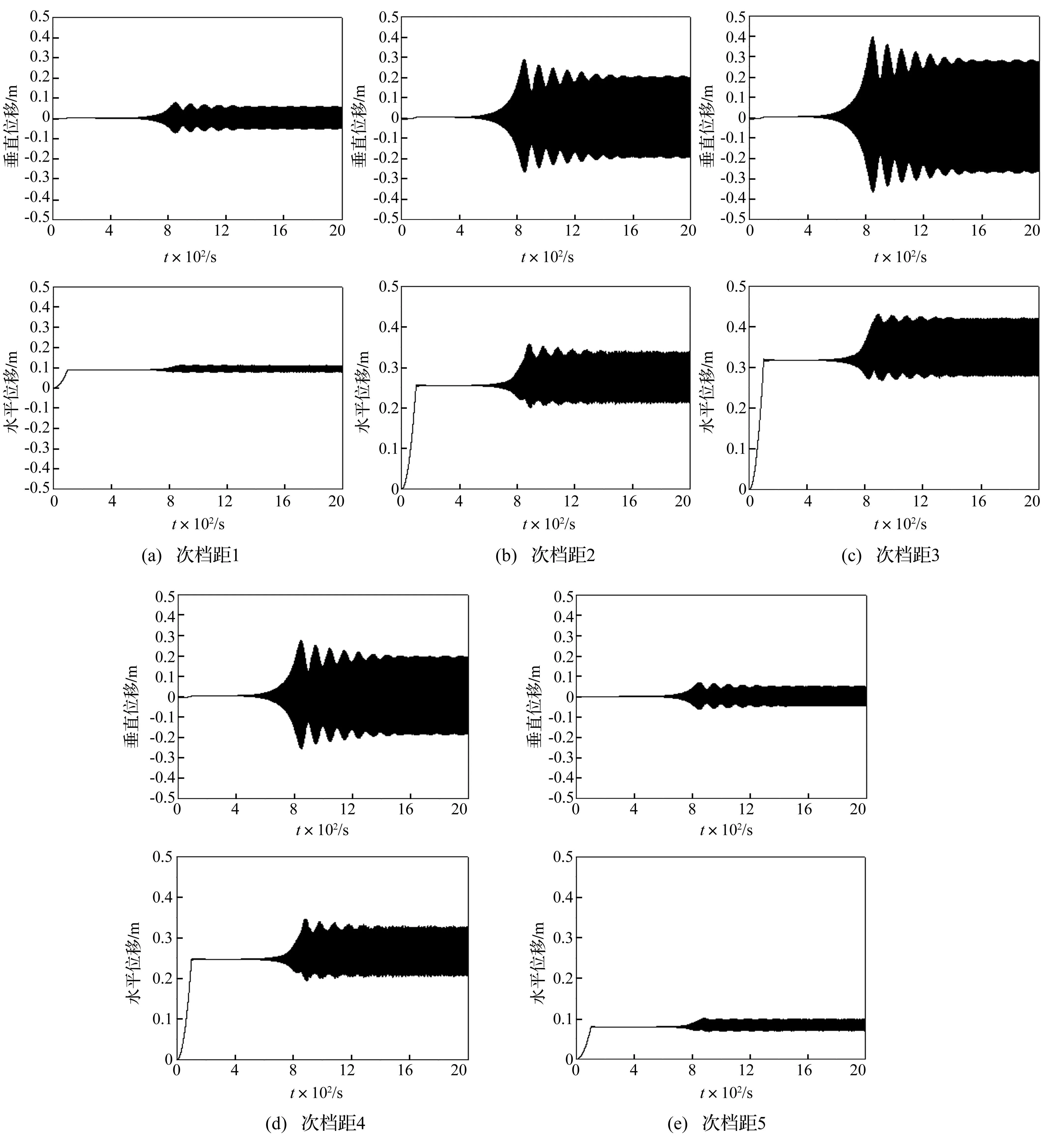
图8　间隔棒非等间距布置时各次档距中点子导线1的位移时程(风速：12 m/s) Fig.8 Time histories of displacements at mid-span of sub-conductor 1 of quad bundle conductor with unequally arranged spacers (wind speed:12 m/s)

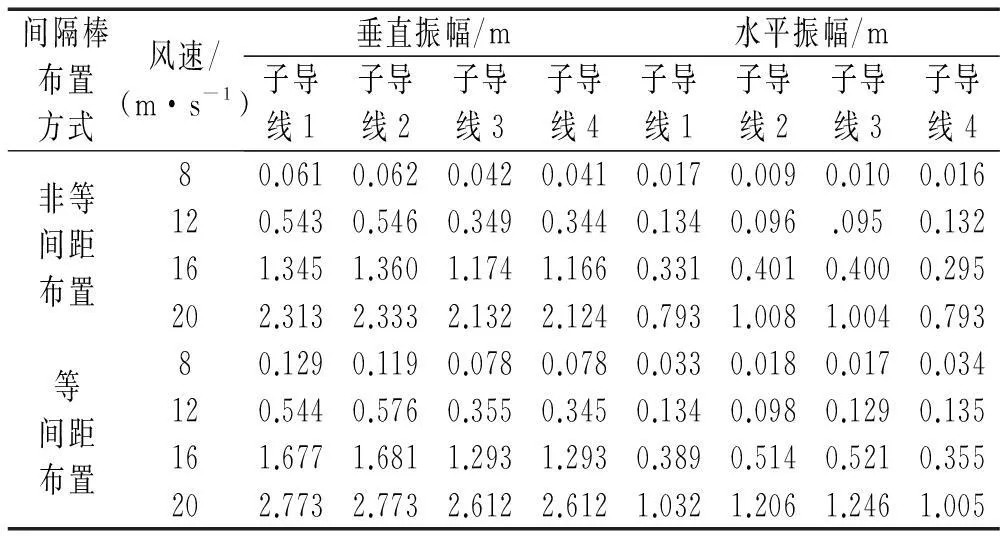
表3　各子导线中点驰振幅值

3.4次档距振动

为了分析次档距振动特性，图8给出了间隔棒非等间距布置时，风速12 m/s情况下各次档距中点子导线1的位移时程；图9为各次档距中点和间隔棒处导线的驰振轨迹。从图中可见，次档距3的中点接近于整档线路的中点，振幅最大，靠近线路两端的次档距1和5的中点的振幅最小。另外，从图9可见，处于上方的两根子导线1和4按逆时针方向运动，而下方的两根子导线2和 3则按顺时针方向运动。子导线的反向运动可能引起现场观察到的“鞭击”现象。

图9　间隔棒非等间距布置时各次档距中点各子导线驰振轨迹(风速：12 m/s) Fig.9 Galloping traces of quad bundle conductor with unequally arranged spacers (wind speed:12 m/s)

图10 间隔棒非等间距布置时子导线1次档距3中点位移频谱(风速:12m/s)Fig.10Displacementspeetraaatthirdsub-spanofsub-conductor1ofquadbundleconductorwithunequallyarrangedspacers(windspeed:12m/s)图11 间隔棒非等间距布置时尾流驰振过程中导线左端的张力变化(风速:12m/s)Fig.11Timehistoriesoftrnsionsinquadbundleconductorwithunequallyarrangedspacers(windspeed:12m/s)

图10给出了间隔棒非等间距布置时，子导线1 在次档距3中点处的位移频谱分析结果，可见，在0.45 Hz、0.93 Hz和1.4 Hz处出现频率峰值。第一个峰值对应于整档的单半波振动形态，第二个峰值接近于三半波固有频率。由图4中给出的次档距局部模态可知，第三个峰值对应于次档距振动模态响应。

文献[5]指出，大多数的观察表明，次档距振动发生时，一对子导线的运动反相，振动幅值接近，且以在1～4 Hz频率范围的低阶次档距模态运动。图8中给出的导线运动轨迹以及振动频率分析结果也反映了这一现象，验证了本文数值模拟结果的合理性。

3.5尾流驰振过程中导线的张力

图11所示为风速12 m/s时，间隔棒非等间距布置时线路在尾流驰振过程中导线左端的张力随时间的变化。可以看出，该点在平衡状态时所有子导线的张力为30.15 kN；驰振过程中处于迎风侧的子导线1和2的峰值大于背风侧的子导线3和4的峰值，从表3和图8中结果可知，子导线1和2的垂直振动幅大于子导线3和4的垂直振动幅值，张力和振幅的变化规律一致。此外，子导线1、2、3、4的最大张力分别为33.20 kN、33.08 kN、32.13 kN、32.22 kN。所有四根子导线的最大张力均约为平衡状态时的1.1倍。由此可见，导线在尾流驰振过程中的张力远小于其抗拉强度，因而由尾流驰振引起的导线断裂应该是疲劳破坏所致。

4结论

本文利用风洞实验测量了四分裂导线的气动系数随风攻角的变化规律，首次利用数值方法模拟了四分裂导线的尾流驰振过程。得到如下结论：

(1)当子导线处于上风子导线的尾流区时，作用于其上的阻力会下降，同时会受到升力的作用；作用于导线上的扭矩非常小，可以忽略不计。

(2)四分裂导线的尾流驰振，除了次档距振动外，还可能发生整档舞动。

(3)采用间隔棒均匀布置方案时，尾流驰振的幅值大于非均匀布置方案。

(4)风速越大，达到稳定驰振状态所需的时间越短，即越易激发尾流驰振。

(5)尾流驰振过程中，四根子导线的振动幅值和张力存在差异，且各子导线的运动方向可能不一致，造成“鞭击”现象。(6)尾流驰振过程中导线的交变应力是引起导线疲劳断裂的原因之一。

参考文献

[1]Brika D, Laneville A. Wake interference between two circular cylinders [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72: 61-70.

[2]Tokoro S, Komatsu H, Nakasu M, et al. A study on wake-galloping employing full aeroelastic twin cable model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88:247-261.

[3]Simiu E, Scanlan R H, Wind effects on structures, third edition, John Wiley & Sons Inc., 1996:237-243.

[4]陈政清，刘慕广，刘志文.基于气弹模型的串列主缆气动干扰试验[J].振动与冲击，2008，27(8)：7-11.

CHEN Zheng-qing, LIU Mu-guang, LIU Zhi-wen. Experiment study on aerodymumic interference of TANDEM cables based on aerodynamic model[J].Journal of Vibration and Shock，2008，27(8)：7-11.

[5]李永乐，王涛，廖海黎.斜拉桥并列拉索尾流驰振风洞试验研究[J].工程力学，2010，27(I)：216-221.

LI Yong-le, WANG Tao, LI Hai-li. Investigation on wake galloping of parallel cables in cable-stayed bridge by wind tunnel test[J].Engineering Mechanics，2010，27(I)：216-221.

[6]Price S J. Wake induced flutter of power transmission conductors[J]. Journal of Sound and Vibration, 1975, 38: 125-147.

[7]Wardlaw R L, Cooper K R, Ko R G,et al. Wind tunnel and analytical investigation into the aeroelastic behaviour of bundled conductors[J]. IEEE Transactions on Power Apparatus and Systems, 1975,2:642-651.

[8]Braun A L, Awruch A M. Aerodynamic and aeroelastic analysis of bundled cables by numerical simulation[J]. Journal of Sound and Vibration, 2005, 284: 51-73.

[9]Yan B, Lin X S, Luo W, et al, Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load[J]. IEEE Transactions on Power Delivery, 2010，25(1)：248-259.

[10]Hu J, Yan B, Zhou S, et al.Numerical investigation on galloping of iced quad bundle conductors[J]. IEEE Transactions on Power Delivery，2012，27(2)：784-792.

[11]国家电力公司东北电力设计院，张殿生，电力工程高压送电线路设计手册，第2版[M].北京：中国电力出版社，2003.

[12]Barbieri N, Honorato de Souza O. Jr., Barbieri R. Dynamic analysis of transmission line cables. Part Ⅰ-linear theory[J]. Mechanical Systems and Signal Processing, 2004, 18:659-669.

[13]Barbieri N, Honorato de Souza O. Jr., Barbieri R. Dynamic analysis of transmission line cables. Part Ⅱ-damping estimation[J]. Mechanical Systems and Signal Processing, 2004, 18:671-681.