考虑流固耦合的弹性圆柱体涡激振动研究

考虑流固耦合的弹性圆柱体涡激振动研究

曹淑刚，黄维平，顾恩凯

(中国海洋大学山东省海洋工程重点实验室，青岛266100)

摘要：利用CFX软件对质量比为7和3.24时圆柱体两向自由度涡激振动进行数值模拟，捕捉到了“锁定区”、“拍”和“相位开关”等现象，探讨了质量比对涡激振动的影响。最终通过研究表明：流固耦合在圆柱体涡激振动分析中应予以考虑；质量比为3.24时的锁定区范围、最大横向振幅以及达到锁定时的流速要比质量比为7时的大；质量比为7时顺流向频率一直为横向频率的2倍，但当质量比为3.24时，顺流向频率在较低约化速度(Ur≤4)下为横向频率的2倍，在较高约化速度下有两个值，一个为横向频率的2倍，另一个与横向频率接近。

关键词：涡激振动；流固耦合；CFX；锁定区；相位开关

中图分类号:U674文献标志码：A

基金项目：国家自然科学基金资助项目(51275080)

收稿日期：2013-11-08修改稿收到日期：2014-01-09

Vortex-inducedvibrationofanelasticcylinderconsideringfluid-structureinteraction

CAO Shu-gang, HUANG Wei-ping, GU En-kai (ShandongKeyLaboratoryofOceanEngineering,OceanUniversityofChina,Qingdao266100,China)

Abstract:The in-line and cross-flow vortex-induced vibration(VIV) of a circular cylinder was simulated using CFX software, with the mass ratio of 7 and 3.24. The lock-in, beat and phase switch phenomena were caught and effects of mass ratio on VIV were discussed. The results show that fluid-structure interaction(FSI) should be considered in the analysis of VIV of cylinder. The range of lock-in, the maximum transverse amplitude and the velocity to achieve lock-in with the mass ratio of 3.24 are larger than those with the mass ratio of 7.The frequency of in-line VIV is always twice of that of cross-flow VIV when the mass ratio is 7. However, when the mass ratio is 3.24, the frequency of in-line VIV is twice of that of cross-flow VIV only at lower velocity reduction (Ur≤4). And there appear two frequencies at higher velocity reduction, the one is twice of frequency of cross-flow VIV, the other is close to that of cross-flow VIV.

Keywords:VIV;fluid-structureinteraction;CFX;lock-in;phaseswitch

随着海上油气开发进入深水，立管的涡激振动已经成为决定其疲劳寿命的关键因素，科学家们正以极大的热情对涡激振动现象及其影响展开研究。Khalak和Williamson[1-4]对两向自由度圆柱体涡激振动进行了研究，发现了“2T”涡旋脱落模态。Dahl等[5]研究了雷诺数为1.1×104~6×104的圆柱体两向自由度涡激振动，发现横向位移响应幅值最大可达1.35倍直径。Sanchis等[6]研究了低质量比时两自由度圆柱体的涡激振动响应，认为质量比是影响两向涡激振动特性的最重要因素之一。唐友刚等[7]研究了较高雷诺数下圆柱流向与横向耦合涡激振动特性，发现在低质量比情况下，流向的振动会对横向振动产生影响。黄维平等[8-10]提出了非线性涡激振动时域分析模型，并对柔性圆柱体两自由度涡激振动问题进行了深入研究。Martin等[11]等利用物理模型试验研究圆柱体涡激振动特性，指出在一定约化速度范围内，顺流向振动频率几乎是横向频率的两倍。以往研究中很多只重视涡激振动横向的动力响应，顺流向的振动特性常被忽略，本文在前人研究的基础上，对不同质量比下圆柱体两向自由度涡激振动特性进行数值模拟，利用CFX软件分析质量比为7和3.24时圆柱体涡激振动的两向位移幅值、升阻力系数等随约化速度的变化，对流固耦合在立管涡激振动分析中的作用，质量比对锁定区范围、最大横向振幅以及两向振动频率的影响进行分析。

1模型建立及分析方法

实验模型包括圆柱体模型和流场模型，圆柱体模型长度取为1m，直径D取为0.03m，流场区域大小为40D×20D，其中圆柱上游区域为10D，圆柱后方尾流区域为30D，如图1所示。圆柱体模型在workbench中建模并划分网格，流场模型先在workbench中建模，然后利用ICEM模块划分网格。本文中流场网格划分了30万个左右，圆柱体网格5 000个左右，为了更好的保证圆柱体表面流动分离的模拟，在接触面周围边界层进行了局部加密。流场左侧采用速度入口边界，输入来流速度；右侧采用流出边界，自由出流，相对压力为0；左右边界采用symmetry边界，圆柱体接触面采用interface边界；上下壁面采用无滑移壁面边界(Noslipwall)。

图1　流场模型和圆柱体模型 Fig.1 Flow field model and the cylinder model

在圆柱体涡激振动计算时采用的是双向耦合，首先在CFX中用流场分析模型进行结构周围以及流场的速度-压力隐式耦合计算，再将流场计算得到的压力分布结果传递给结构模型进行强度分析；然后利用ANSYS模块对结构进行受力及变形分析，最终将分析结果传递给CFX模块，再进行下一个耦合过程的流场分析，这样就完成了一个迭代过程，同时完成了流场数据和结构数据的交换。

2固定圆柱体绕流分析

图2给出了Re=200时固定圆柱绕流升阻力系数曲线图，从图中可以看出，阻力系数Cd随着时间步增加逐渐增大并稳定在1.35左右，升力系数Cl幅值稳定在0.5左右。通过与以前经典结果(表1)对比可知，固定绕流时有足够的精度，这确保了后面流固耦合计算时CFD模拟的正确型。

图2　Re=200时升阻力系数 Fig.2 C land C dunder Re =200

表1　圆柱绕流结果校核( Re=200)

3弹性圆柱体涡激振动响应分析

3.1质量比为7的圆柱体涡激振动分析

控制涡激振动的主要参数是约化速度Ur，本文将就不同约化速度下圆柱体涡激振动的特性进行讨论。此时如果采用钢质立管属性，得到一阶固有频率为136.9Hz，当Ur=1时，流速u=4.107m/s，可知此条件下速度过大，既超过实际环境可能的流速也不能顺利进行流固耦合计算，因为网格变形过大会导致计算无法进行。因此本文把圆柱体弹性模量修改为E=2.07e8Pa，此时模型的一阶固有频率为4.329Hz。圆柱体的弯曲刚度k=EI/l3，为了保证模型圆柱体可以模拟实际立管的振动性质，只需保证两者的弯曲刚度相同即可，常用的实际立管直径为0.3m左右，此时可以模拟的实际立管长度约为215m。

图3　流固耦合对升阻力系数的影响 Fig.3 FSI effects on C land C d

同一流速下考虑与不考虑流固耦合时的振动特性，如升阻力系数、涡旋脱落状态会有所不同，为了研究流固耦合对升力及阻力的影响，图3给出了u=0.123m/s时考虑与不考虑流固耦合的升阻力系数曲线图。从图中可以看出考虑与不考虑流固耦合时的升力系数与阻力系数的变化趋势还是相同的，但两者的升阻力系数的大小具有明显不同，考虑流固耦合时的阻力系数比固定时的阻力系数小0.1左右，升力系数比固定时大，这说明考虑流固耦合对流场以及升阻力的变化是有影响的，并且影响效果不一致，因此，在研究圆柱体动力响应时应该考虑流固耦合作用。

图4给出了Ur=1时模型的两向位移时程曲线，此时对应的流速u=0.13m/s，从图中可以看出此时顺流向位移大于横向位移，顺流向位移均值大约稳定在0.72×10-4m左右，横向位移幅值先增大，然后缓慢降低并趋于稳定，幅值大小约稳定在0.55×10-4m左右。图5给出了Ur=1时的两向位移功率谱，从图中可以看出，此时横向频率大约在1.5Hz左右，远远小于结构固有频率4.329Hz，说明此时还未进入锁定区范围，此时顺流向频率为横向频率的2倍。

图4　U r=1时位移时程曲线 Fig.4 Time history of displacement under U r=1

图5　U r=1时位移响应的功率谱 Fig.5 Power spectra of displacement under U r=1

“拍”现象是涡激振动中一种不太常见的物理现象，产生的必要条件是两个振动的频率比较接近，这时位移响应或升力系数的值随时间时而增大时而减小，表现出调谐状态，在约化速度Ur=3时，成功捕捉到了拍现象，如图6所示。从图中可以看出升力系数Cl随着时间步长的增加时而增大时而减小，这是涡激振动重要的现象之一。

图6　“拍”现象 Fig.6 “Beat” phenomenon

当约化速度Ur=5时已进入锁定区，图7给出了Ur=5时两向位移时程曲线，从图中可以看出，此时顺流向位移大约在0.003m左右，横向位移大约在0.016m左右，顺流向位移与横向位移都比Ur=1时显著增大，且横向位移增大的更快，横向位移幅值已经超过顺流向位移均值。从图8的位移响应功率谱中可以看出，此时横向振动频率与结构的固有频率4.329Hz相近，此时顺流向频率仍为横向频率的2倍。在锁定区内涡旋脱落频率基本和圆柱体的固有频率保持一致，涡旋脱落频率不再满足斯托哈尔数为常数的规律，即约化速度增加，涡旋脱落频率不再增加，但圆柱的横向位移响应幅值会显著增加。

图7　U r=5时位移时程曲线 Fig.7 Time history of displacement under U r=5

图9(a)给出了圆柱体两向振幅随约化速度的变化关系图，图9(b)为Carberry和Sheridan[12-14]经典实验中横向振幅与约化速度关系图，比较两图可以看出，本文的研究结果与Carberry等的研究结果很吻合，只是锁定区的范围有所不同，Carberry等的锁定区范围对应的约化速度为4.5~7，本文数值模拟时观察到的锁定区范围对应的约化速度约为4.5~6，这可能是由于采用了不同的质量比造成的。

3.2质量比为3.24的圆柱体涡激振动分析

当质量比为3.24时弹性圆柱体的一阶固有频率为6.917Hz，观察到的锁定区范围对应的约化速度约为5~9，对应的流速为1.04~1.87，与质量比为7时相比流速更大，而且锁定区范围有扩大趋势。为了节约篇幅下面只就与质量比为7时的主要不同现象进行分析。图10给出了Ur=5时圆柱体的位移响应功率谱，该约化速度已在锁定区范围内。从图中可以看出此时顺流向振动有两个主要的频率，前一个频率与横向频率接近，后一个频率约为横向频率的两倍，且此时横向频率与结构固有频率6.917Hz相近，观察质量比为3.24时所有不同约化速度下的位移响应功率谱，可以发现当约化速度小于4时，顺流向振动频率为横向振动频率的两倍，当约化速度为5时，顺流向振动呈现变频率的特点，首先以两倍横向频率振动，然后以一倍横向频率振动，在后边更大的约化速度下也呈现出这个特点。而在前面质量比为7的涡激振动中，顺流向振动频率一直为横流向的两倍，这说明质量比除了影响锁定区范围外还影响顺流向的振动频率。

图8 Ur=5时位移响应的功率谱Fig.8PowerspectraofdisplacementunderUr=5图9 振幅与约化速度关系图Fig.9RelationshipbetweenamplitudeandUr图10 Ur=5时位移响应功率谱Fig.10PowerspectraofdisplacementunderUr=5

图11给出了Ur=5时的位移时程图，从图中发现，时间步300步之前，横向位移随时间增加而增大，达到峰值后横向位移缓慢的降低直到一个较稳定的值，这个现象体现了立管涡激振动的自限性，圆柱体振动达到一定程度时，对流场的扰动增强，破坏了涡旋的脱落形态，流场的变化又反过来影响圆柱体的振动，这个特性使得结构的横向振幅不会一直变大，而是最终稳定在某个范围内，从图中还可以发现此时横向位移最大值超过了1.1倍直径，而在质量比为7时，在所有约化速度中的最大值也只有0.7倍左右，说明质量比对横向振幅所能达到的最大位移影响很大。

图11　U r=5时位移时程曲线 Fig.11 Time history of displacement under U r=5

涡激振动中有一个现象叫做“相位开关”，指的是结构的升力系数和位移响应曲线的相位从原来的“同相”转变成了“反相”。在质量比为7时，锁定区和非锁定区都没有发现这个现象；在质量比为3.24的情况下，当约化速度较小时升力系数和位移响应基本保持同相，但当约化速度Ur=7时，我们观察到了“相位开关”，如图12所示，图中实线代表横向位移响应，虚线代表升力时程曲线，可以看出结构横向位移响应相位与升力系数相位刚好相反。“相位开关”的现象可能由于系统的阻尼使流体作用力和结构位移的变化不能保持一致造成的。

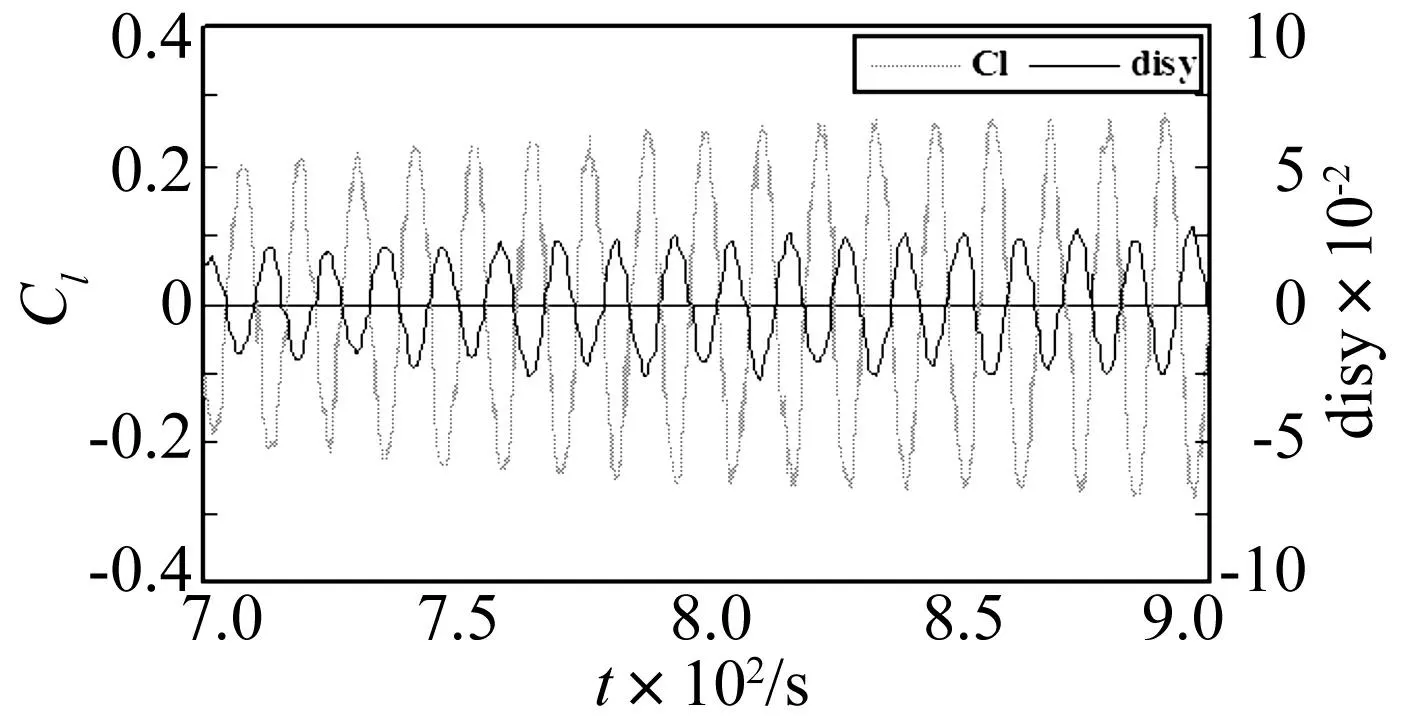
图12　相位开关 Fig.12 Phase switch

4结论与展望

本文借助CFX流固耦合方案研究圆柱体涡激振动特性，最终通过数值模拟研究了质量比为7和3.24时不同约化速度下圆柱体的位移响应功率谱、两向振幅、升阻力系数等的变化，并发现了“拍”和“相位开关”的现象。通过分析发现流固耦合在立管涡激振动研究中应予以考虑；质量比对锁定区的范围、最大横向振幅以及顺流向振动频率都有影响。质量比为3.24时的锁定区范围、最大横向位移要比质量比为7时的大，而且达到锁定时的流速比质量比为7时的也要大；质量比为7时顺流向频率一直为横向频率的2倍，但当质量比为3.24时顺流向频率在较低约化速度(Ur≤4)下为横向频率的2倍，在较高约化速度下有两个值，一个为横向频率的2倍，另一个与横向频率接近。

由于数值模拟本身的局限，研究可能会存在一些不完善之处，研究结果也只是一些初步认识，要真正了解深水圆柱体涡激振动的本质以及质量比的影响有待于进一步的研究，以后的研究中可加入相应的物理模型试验，两种方法相互验证以提高结果的准确性。

参考文献

[1]KhalakA，WilliamsonCHK.Motions，forcesandmodetransitionsinvortex-inducedvibrationsatlowmass-damping[J].JournalofFluidsandStructures，1999，13:813-851.

[2]JautisN，WilliamsonCHK.Vortex-inducedvibrationofacylinderwithtwodegreesoffreedom[J].JournalofFluidsandStructures，2003，17: 1035-1042.

[3]WilliamsonCHK，JautisN.Ahighamplitude2Tmodeofvortex-inducedvibrationforalightbodyinXYmotion[J].EuropeanJournalofMechanicsB/Fluids， 2004，23:107-114.

[4]JautisN，WilliamsonCHK.Theeffectoftwodegreesoffreedomonvortex-inducedvibrationatlowmassanddamping[J].JournalofFluidsandStructures，2004，509: 23-62

[5]DahlJM，HoverFS，TriantafyllouMS.Two-degree-of-freedomvortex-inducedvibrationsusingaforceassistedapparatus[J].JournalofFluidsandStructures，2006，22: 807-818.

[6]SanchisA，SlevikG，GrueJ.Two-degree-of-freedomvortex-inducedvibrationsofasping-mountedrigidcylinderwithlowmassratio[J].JournalofFluidsandStructures，2008，24: 907-919.

[7]唐友刚，樊娟娟，张杰,等. 高雷诺数下圆柱顺流向和横向涡激振动分析[J]. 振动与冲击，2013，32(13):88-92.

TANGYou-gang，FANJuan-juan，ZHANGJie，etal.Inlineandtransversevortex-inducedvibrationanalysisforacircularcylinderunderhighReynoldsnumber[J].JournalofVibrationandShock，2013，32(13):88-92.

[8]黄维平，刘娟，唐世振. 考虑流固耦合的大柔性圆柱体涡激振动非线性时域模型[J]. 振动与冲击，2012，31(9) : 140-143.

HUANGWei-ping，LIUJuan，TANGShi-zhen.Nonlinearmodelofvortexinducedvibrationofflexiblecylinderinconsiderationoffluid-structureinteraction[J].JournalofVibrationandShock，2012，31(9):140-143.

[9]范杰利，黄维平. 细长立管两向自由度涡激振动数值研究[J]. 振动与冲击，2012，31(24):65-68.

FANJie-li，HUANGWei-ping.Numericalsimulationof2-DOFvortex-inducedvibrationofalongriser[J].JournalofVibrationandShock，2012，31(24):65-68.

[10]唐世振，黄维平，刘建军,等. 不同频率比时立管两向涡激振动及疲劳分析[J]. 振动与冲击，2011，30 (9) : 124-128.

TANGShi-zhen，HUANGWei-ping，LIUJian-jun,etal．Vortexinducedvibrationandfatiguedamageofrisersundertwo-dimensionalvortexexcitationconsideringdifferentfrequencyratios[J].JournalofVibrationandShock，2011，30(9):124-128.

[11]MartinS.Experimentalinvestigationofin-lineandcross-flowVIV[C].Presentedon13thInternationalOffshoreandPolarEngineeringConference，Honolulu，Hawaii，USA，2003，May25-30.

[12]CarberryJ，SheridanJ，RockwellD.Forcesandwakemodesofanoscillatingcylinder[J].JournalofFluidsandStructures，2001，15( 3-4) : 523-532.

[13]CarbenyJ，SheridanJ，RockwellD.Cylinderoscillationsbeneathafree-surface[J].EuropeanJournalofMechanicsB/Fluids，2004，23: 81-88.

[14]CarberryJ，GovardhanR，SheridanJ，etal.Wakestatesandresponsebranchesofforcedandfreelyoscillatingcylinders[J].EuropeanJournalofMechanicsB/Fluids，2004，23: 89-97.

第一作者李允公男，博士，副教授，1976年生