协整系数矩阵的非平稳工程系统故障诊断应用研究

协整系数矩阵的非平稳工程系统故障诊断应用研究

石海忱，陈前，林原灵

(南京航空航天大学机械结构力学及控制国家重点实验室振动工程研究所，南京210016)

摘要：对于非平稳工程系统，若系统变量是一阶单整的，则可以建立变量间的协整关系模型，通过理论分析证明，协整系数矩阵可作为故障空间的特征参数用作系统的故障诊断。非平稳系统变量首先要通过单位根检验以证明其一阶单整，然后使用Johansen检验法估计出协整系数矩阵，即特征参数，使用一对多分类的支持向量机(SVM)算法进行故障数据的训练和测试。使用液压舵面故障仿真系统作为试验平台，使用输入指令、舵面角度等5个一阶单整的系统变量作为协整变量，其估计出的协整系数矩阵作为特征参数，结果表明协整系数矩阵作为特征参数，SVM作为数据分类方法，具有很好的故障分类效果。

关键词：协整；故障诊断；非平稳；支持向量机(SVM)；液压舵面系统

中图分类号:TP206+.3文献标志码：A

收稿日期：2013-07-08修改稿收到日期：2013-11-11

Faultdiagnosisofnon-stationaryengineeringsystemusingcointegrationcoefficientsmatrix

SHI Hai-chen, CHEN Qian ,LIN Yuan-ling(StateKeyLaboratoryofMechanicsandControlofMechanicalStructures，NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)

Abstract:In terms of the fault diagnosis for non-stationary engineering systems, the cointegration coefficients matrix was proposed as the characteristic parameter if the system variables are integrated of first order. System variables should first be verified to be integrated of first order through unit root test, then Johansen method was used to estimate the cointegration coefficients matrix. The classification algorithm of supporting vector machine (SVM) was used to train the model and test the accuracy of classification. Thus, a new approach applied in non-stationary system was established towards finding a new characteristic parameter for fault diagnosis. This new approach has been applied to the fault diagnosis of a simulated hydraulic flap servo system, using 5 system variables including input orders, flap angle, etc. as the cointegration variables. The test results indicate that the cointegration coefficients matrix model has great fault diagnosis ability for typical non-stationary systems.

Keywords:cointegration;non-stationary;supportingvectormachine(SVM);hydraulicflapservosystem

现代工业设备日趋大型化、复杂化、自动化和连续化,设备各部分的关联愈加密切，某处微小故障就会爆发链锁反应。另外，非平稳随机过程的大量存在使得基于随机平稳随机过程假设下的经典统计检验理论不再适用[1]。目前针对非平稳过程的主要分析方法有短时傅里叶变换、Wigner-Ville分布、Gabor变换、小波变换和Hilbert-Huang变换等，而这些方法多是对单个信号的分析方法[2]。而在复杂的动态工程系统中，子系统故障的发生会使得多个部位都产生故障信息，因此，以单个信号为分析对象的方法所包含的信息对象有限，甚至会造成故障信息的遗失。

协整理论是计量经济学中一种分析多个非平稳随机变量间长期均衡关系的建模方法。Engle和Granger等在面对分析经济非平稳变量时提出了协整算法，把时间序列分析方法中对于模型短期动态设定的优点和计量经济学中长期均衡关系确定的特点融合为一体，成为了经济学领域分析长期均衡关系的常用建模方法。本课题组自2006年以来，首创性地将协整理论这一计量经济学理论成功应用于工程系统状态监测与故障诊断实践，并在石油催化裂化过程仿真模型和发动机仿真模型等工业过程对象上进行了初步的应用，取得了积极的成果[3]。对于协整模型故障诊断方法，潘昱昱等[4]提出了变量轮换和降阶协整模型的方法进行故障诊断与隔离；鲁帆等[5]比较了以最大特征值为准则的单协整模型和以最大信息熵为准则的多协整向量模型对于监测效力的不同反映，最大程度地保留了系统的故障信息，提高了监测效力。同时，一些国外研究者受到本课题组工作的启发，也开始对协整理论的应用产生了兴趣，并且展开了相似的研究工作。Cross等[6]也将协整理论应用为一种新的结构健康监测模型，并在消除时间序列环境趋势方面做了相应研究；Dao等[7]则在Lamb波和小波分析基础上，去除温度环境趋势影响后，再应用协整理论方法来提高故障位置定位精确度。

1基于协整理论的特征提取

上述的几种基于协整理论建模的方法，只能“定性”地描述系统是否发生了故障而无法在故障类别的诊断上发挥效力。对于非平稳系统，采集得到的系统变量往往包含大量数据，因而需要从协整理论模型的变量间提取对故障特征敏感的参数，并选择合适的分类方法进行故障诊断。

1.1协整理论简介

如果一个时间序列在成为稳定序列之前必须经过d>0次差分，则该序列被称为d阶单整(Integration)，记为I(d)[8-9]。即对于非平稳序列yt，Δdyt是平稳序列，而在差分d-1次后仍是非平稳的，那么yt是I(d) 序列。其中，Δ为差分运算子

Δyt=yt-yt-1,Δ2yt=Δ(Δyt),…，

Δdyt=Δ(Δd-1yt)

(1)

因此，平稳序列可表示为I(0)。在实际应用中，主要针对一阶单整序列I(1)进行讨论。

1.2AugmentedDickey-Fuller(ADF)单位根检验

对变量进行协整分析之前，必须对其进行单位根检验，以确定其为非平稳并且是一阶单整的。而目前较为通用的方法为AugmentedDickey-Fuller单位根检验，简称ADF检验。ADF的检验方程为：

Δyt=γyt-1+θ1Δyt-1+θ2Δyt-2+…+

θpΔyt-p+μ+et

(2)

式中，Δyt是yt的差分，γ，θ1，θ2，…θp为常数项，μ为常变量，et为残差。使用最小二乘法对上式进行估计，通过检验式中的系数γ的t统计量，根据不同的显著性水平，检验γ的t统计量是否超过ADF临界值，从而判断序列yt是否是一阶单整。具体的检验过程可参见文献[8-10]。

1.3协整系数矩阵的估计

对于多个变量的协整检验，通常是对其参数进行极大似然估计的Johansen检验[10-11]。建立多变量无约束的向量自回归VAR(n)模型：

Yt=Π1Yt-1+…+ΠnYt-n+ut

(3)

式中:Yt表示包含p个样本长度为T的一阶单整的随机变量序列yi的p×T矩阵。由此得到相对应的误差校正模型(ECM)：

(4)

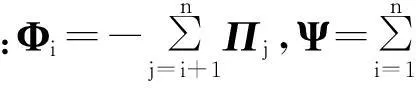
下面使用最小二乘法对下两式进行参数估计：

(5)

(6)

可以得到式(5)和式(6)估计残差构成的矩阵分别为S0和S1。S0、S1均为p×T矩阵。

计算残差矩阵S0和S1的积矩阵：

(7)

最后，对式(8)的特征方程求解

((8)

对求解得到的特征值按照λ1≥λ2≥…≥λp的顺序构成对角矩阵Ω，V1,V2,…Vp为与之相应的特征向量,令矩阵Λ=[V1,V2,…Vp],矩阵Λ的秩为r，则这p个变量间存在r组协整关系可以使得Yt通过线性组合变为平稳。由此便得到了我们所关心的协整系数矩阵的极大似然估计B。

1.4协整系数矩阵作为故障诊断特征参数

根据协整理论，如果系统内一组非平稳过程变量都是一阶单整的，那么就可以建立一个简单的线性协整关系模型。协整的线性组合关系是由系统的内在机制所决定，表征了各个系统变量间的长期平衡关系。故障的发生会破坏原有的动态平衡，形成新的平衡状态，造成系统模型参数或结构的变化，并反映在系统变量之间动态关系上，即故障状态下的变量形成了新的协整关系，变量之间新的共同趋势不再符合正常状态下的协整关系[3,5]。类似于化学反应方程式，反应方程式中的各种物质之间存在着由配平系数决定的“线性关系”，工程系统的各个变量之间也存在着均衡的动态关系，协整线性关系就是反映这种动态关系的理想的特征。当化学反应发生时，反应物质的配平系数也会相应的发生变化。相似的，当工程系统发生故障后，系统原先的动态平衡被打破，动态关系也就发生了变化并且趋向了新的故障状态下的动态平衡。

协整系数矩阵便是表征变量间协整线性关系的理想特征参数，在估计协整系数矩阵的Johansen检验过程中，可以得到特征值方程

(9)

对求解得到的特征值按照λ1≥λ2≥…≥λp的顺序构成对角矩阵Ω，由式(7)、式(8)可得：

(10)

由式(10)可以看到，λi为关于Yt的函数，对应于λi的协整系数矩阵自然也与Yt相关，协整系数矩阵B也便包含了系统变量和变量差分的信息，当系统状态发生改变时，长期动态关系和短期动态关系都会在矩阵B中有所反映，因此可以用来作为表征系统状态的特征参数。然而协整系数矩阵一般为r×T的矩阵，若直接将矩阵B作为故障诊断特征参数，则会在分类器训练时出现维数过高，构造分类器复杂等缺点，为方便使用而又不丢失变量信息，我们可将矩阵重新按行排列为包含了rT个元素的一维数组，以此作为系统故障诊断的特征参数。

2支持向量机分类

通过协整系数矩阵可以从大量的数据中提取出表征系统状态的特征参数，故障诊断的下一步则是要对这些特征参数进行有效的分类。

2.1支持向量机简介

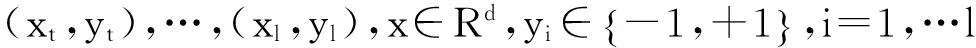
图1　最优分类面 Fig.1 Optimal classification hyperplane

支持向量机主要针对二值分类的问题，在高维空间中寻找一个超平面作为两类的分割，以保证最低的错误分类率。因此，SVM算法十分适合协整系数矩阵构成的高维状态空间的分类问题。

2.2支持向量机用于多分类

由于支持向量机在分类问题上只考虑了二值分类，对于常见的系统故障诊断往往需要多值分类，因此需要建立多个SVM分类器。基于二值分类算法，Platt提出了一个新的学习架构：有向无环决策图(DecisionDirectedAcyclicGraph，DDAG)方法，使得支持向量机能适用于多分类[13]。以本文中所应用的液压舵面系统为例，系统存在正常(N)、泄漏故障(L)、阻尼故障(C)、刚度故障(K)等。据此，我们构造了4种状态下的SVM多分类器，图2中每一个方框代表了一个SVM二值分类器。输入数据通过每一层的分类器后都会流入下一层的不同的分类器进行决策和分类，通过这种多分类器结构，可以有效减少分类重叠现象和不可分类现象的出现，对于存在n种状态的故障诊断系统，可参照这个结构进行扩展。

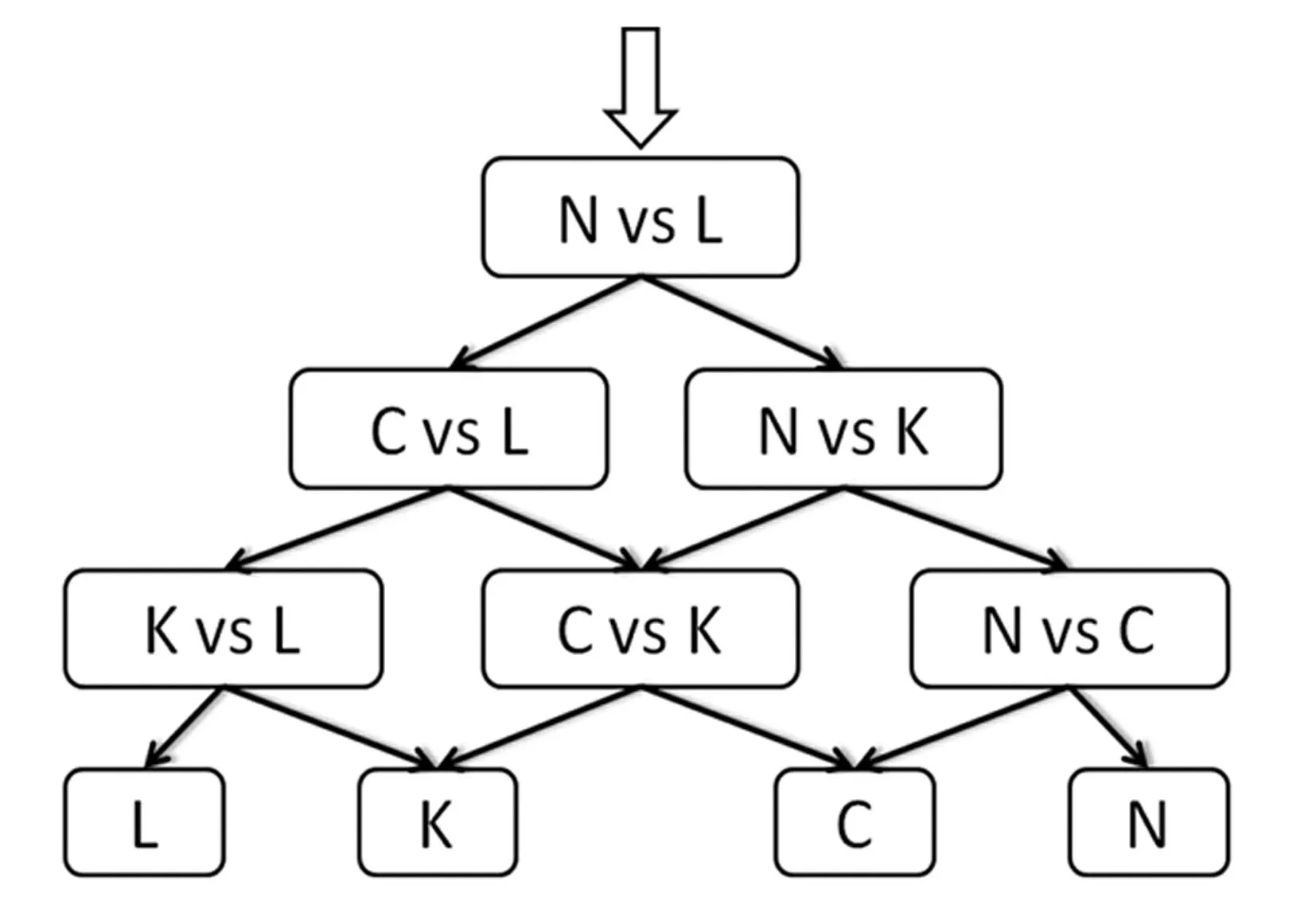
图2　DDAG方法结构示意图 Fig.2 Decision directed acyclic graph

3协整系数矩阵应用于故障诊断的一般步骤

由上文的协整理论可知，协整系数矩阵模型是对工程中常见的一阶单整的非平稳变量所建的模型，协整理论建模方法是从计量经济学中发展而来的，常见金融时间序列一般都是一阶单整的，然而协整理论建模方法在工程背景下的应用仍处于探索阶段，因为工程领域的信号更加复杂，一阶单整的信号主要出现在相对低频缓变的工程系统中，主要应用有化学流程工业、汽车发动机电控汽油喷射系统等的故障诊断，大坝结构安全以及高速公路大桥的状态监测[3-4,15]。对于高阶单整的时间序列或平稳的时间序列，如果也想使用协整理论进行建模，则可通过一定的数学变换如积分或差分等构造一阶单整序列。因此，将协整理论建模方法推广到更多工程系统，仍需要结合计量经济学的发展，进行更深入的理论与试验研究。

由此，可以总结应用协整系数矩阵进行故障诊断的一般步骤为：

①对于一个非平稳系统，使用传感器和数据采集设备对其进行采样以及预处理；

②结合系统数学模型，选取对系统固有频率等动态特性影响较大或包含环境趋势的系统变量，如压力，位移，温度等。以下文中液压舵面系统的数学模型为例，由文献[16]可知其固有频率与输入曲线、舵面角度等变量有关，则选取它们作为协整变量；

③对协整变量和变量的一阶差分进行ADF单位根检验，从中筛选出一阶单整的变量；

④对上述一阶单整变量进行协整检验—Johansen检验，其中VAR模型的最佳滞后阶数由上一步中确定，并由此得到了特征参数即协整系数矩阵；

⑤以协整系数矩阵建立训练样本，建立SVM分类器；

⑥以SVM分类器为基础，搭建DDAG多值分类器；

⑦将输入数据输入给分类器便能得到诊断结果。

4协整系数矩阵在液压舵面仿真系统故障诊断中的应用

4.1液压舵面仿真系统故障仿真试验

该仿真系统是基于Labview软件平台下设计的，对液压舵面系统中主要组成部件建立了动态微分方程的数学模型。系统主要包括反馈控制器、液压伺服阀、液压作动筒、舵面偏转机构等。在本次故障仿真试验中，为能保证每一组中对不同状态参数进行多次重复试验和对比研究，我们让每一组试验的输入曲线都相同，同时设计了4种仿真状态：”N”，”L”，”C”，”K”，分别对应着“正常状态”，“泄漏故障”，“阻尼故障”，“刚度故障”，而每一种状态分别取了20组状态参数各不相同的仿真数据：其中“泄漏故障”取了从2倍到21倍正常状态泄漏系数20组仿真数据；“阻尼故障”取了从1.5倍到11倍正常状态轴承阻尼系数的20组仿真数据；“刚度故障”取了从0.2倍到1.2倍正常状态扭转刚度的20组仿真数据。在时间步长为0.000 1s下，仿真软件产生了20s长度，2×105点的仿真数据，并从中选择了包括输入指令、舵面角度、摇臂角度等19个系统变量进行保存。由于协整理论要求随机变量为非平稳并且是一阶单整的，选取对系统固有频率特性影响较大的变量同时去除系统变量间存在几何关系的变量，最终选取了输入指令I，舵面角度θ，摇臂角度α以及两个构造的虚拟位移Z1,Z2一共5个协整检验变量。

4.2协整系数矩阵的提取

从仿真数据可以看到，每个系统变量的样本数据有2×105点，若不提取特征参数而直接分类，则对分类器的要求过高，分类效果可想而知。对5个系统变量建立协整关系模型，提取出协整系数矩阵作为特征参数，大大降低了状态空间的维数，提高了故障诊断的可行性。

4.2.1ADF单位根检验

对系统变量进行ADF单位根检验就是要验证变量为非平稳且是一阶单整的，并依据检验结果确定模型的最佳滞后阶数。根据样本序列曲线分析，在ADF检验中使用了包含时间趋势项和截距项的向量自回归模型。表1所示为0.5倍刚度故障状态下的ADF检验表，选择了输入指令I，舵面角度θ等5个系统变量，通过ADF检验发现这5个变量在5%的置信水平下均为非平稳变量，将其取一次差分之后再检验则都变为了平稳变量，说明这5个系统变量均为一阶单整的随机变量，表1中还给出了各个变量VAR模型的最佳滞后阶数。

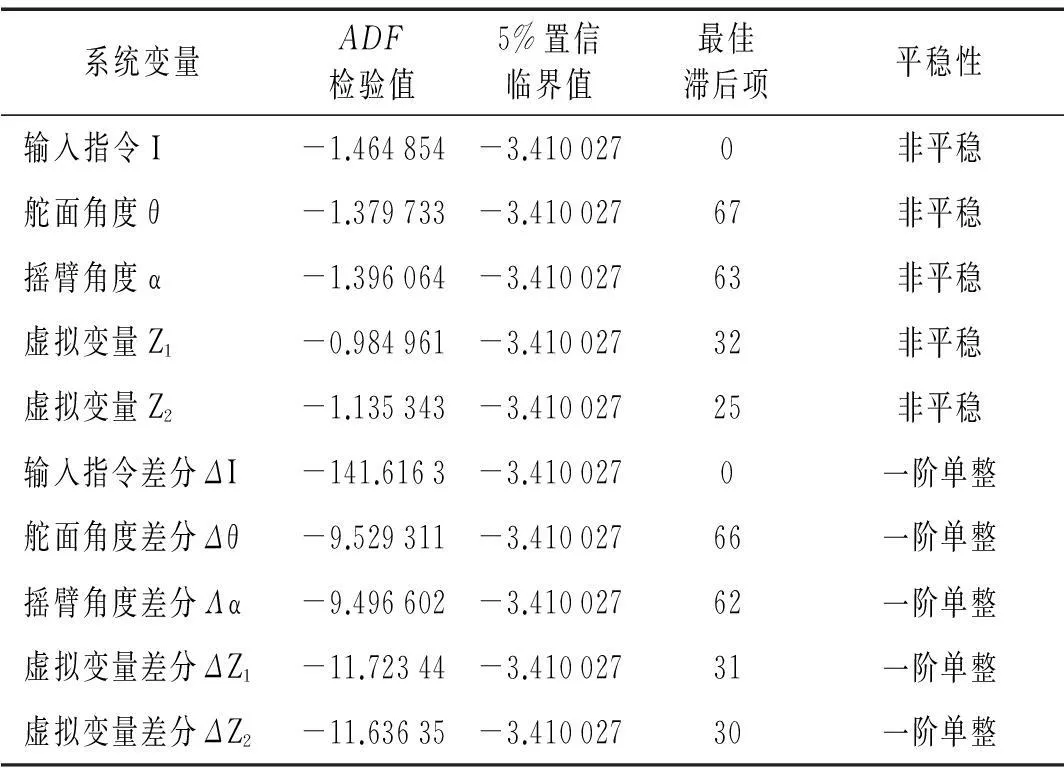
表1　0.5倍刚度故障状态的 ADF单位根检验

4.2.2Johansen检验

使用1.3节所述的检验方法，分别对5个变量进行Johansen协整检验，以确定变量间存在协整关系的个数，同时估计出协整系数矩阵B，检验中VAR模型的最佳滞后阶数由上步中ADF检验得到。以“0.5倍刚度故障”为例，Johansen检验表明该故障状态下，变量在5%的置信水平下存在4组协整关系。以AIC最大为准则确定其VAR模型的最佳滞后阶数，检验结果如表2所示：

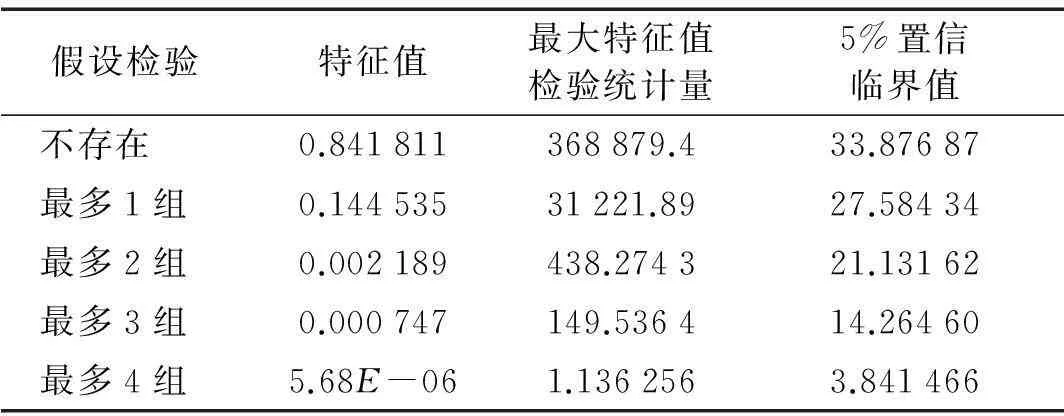
表2　0.5倍刚度故障状态的最大特征值 Johansen检验

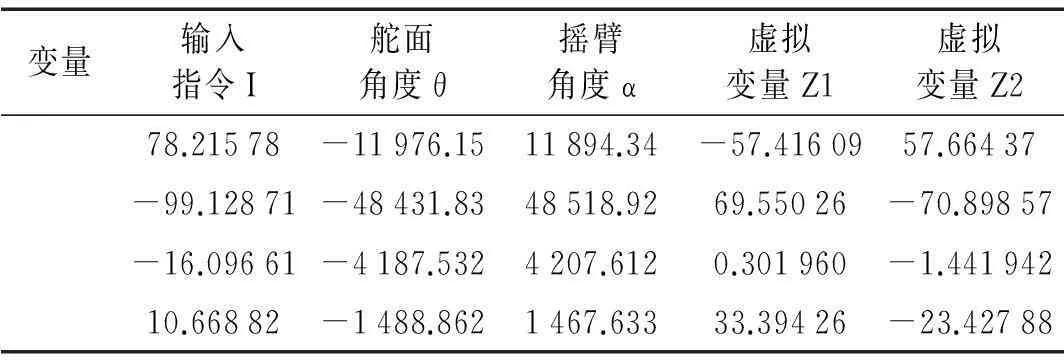
表3　0.5倍刚度故障状态的协整系数矩阵

使用1.3节所述方法，使用最小二乘法估计出这5个变量间存在的4×5协整系数矩阵B，即变量与协整系数矩阵B可以构成4组平稳变量，变量间的动态平衡关系通过线性组合的方式建立了模型。为方便对其进行分类，将4×5的协整系数矩阵按行整理成1×20的一维数组，由此便得到了故障诊断所需要的特征参数。

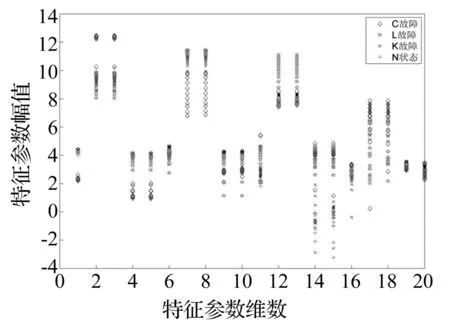
图3　各状态特征参数幅值对比 Fig.3 Amplitude comparison of characteristic parameters under different status

将所有状态样本的特征参数幅值进行对比，如图3所示，4种系统状态的特征参数有较明显的分类出现，如阻尼故障(C故障)状态下，特征参数在某几个维度下与其余状态特征参数幅值分类明显；正常状态特征参数幅值变化范围相对较小，3种故障状态下的特征参数幅值变化都比较大。注意到在某些维数下，4种状态下特征参数的幅值出现了交叉，易造成错误分类，因而有必要使用适合高维空间小样本分类的支持向量机算法。

4.3基于SVM的故障分类与结果

得到了系统的特征参数之后便可以对系统的状态进行判别了。从每一个状态下的20组仿真数据中选择了12组作为训练数据，8组作为测试数据，即一共48组训练数据，32组测试数据。由于每一组协整向量都有12个，因此协整向量所张成的特征空间也是12维的，因此不可能通过可视化的方式看到分类结果。

将训练数据输入给SVM分类器进行训练，N、C、L、K为系统4种不同的状态，每两种状态间都训练出一个SVM二值分类器，这样便能得到6个不同状态间的SVM分类器，使用1.5.2节中所述的一对多的DDAG方法搭建多值分类器。训练中，SVM网络核函数选择为RBF径向基函数，带宽参数设置为2，容错惩罚值设置为10。训练完成后，将剩下的8组仿真数据进行测试，测试的准确率达到了96.8%，也就是32组测试数据中仅有一组发生了误报，如表4所示，DDAG输出结果在刚度故障状态里发生了一次误报，说明在训练样本数量有限的情况下，SVM分类器达到了很好的分类效果。

表4　 DDAG分类结果

5特征参数的降维

在液压舵面伺服仿真系统中，作为特征参数的协整系数矩阵有12个元素，虽然使用SVM分类方法取得了很好的分类效果，但是在更普遍的工业系统中，若系统的非平稳单整变量有n个，估计出的协整系数矩阵的元素为rn(r为n个变量间存在的协整关系个数)，随着n的增大，特征参数的维数也迅速变大，并且无法使分类结果可视化，因此有必要对协整系数矩阵进行降维。考虑到协整系数矩阵张成的空间构成了系统的状态空间，我们尝试使用表征矩阵广义距离的∞范数和F范数来作为特征参数。图5给出了各种状态下，协整系数矩阵的∞范数作为横轴，F范数作为纵轴的分类情况，可以看到各种状态的分类效果非常好，各状态分布在平面的不同区域，并没有出现交叉重叠的状况，仅仅是刚度故障出现了2个离群值。注意到这与第4节中仅有一组误报的结果不一致，只是由于SVM分类器设置了容错惩罚值为10，使得刚度故障状态下的分类超平面恰好只错分了一个离群值。并且从协整系数矩阵中提取∞范数和F范数作为特征参数也损失了一定的信息，结合仿真试验可知刚度故障离群值是刚度为0.2倍与0.25倍正常状态下的样本点，低刚度状态在实际情况中并不多见，系统在达到低刚度状态前可能已经发生了破坏，因而仅能用作仿真试验中的故障发展趋势研究，这也从侧面佐证了中协整系数矩阵模型诊断结果的准确性。

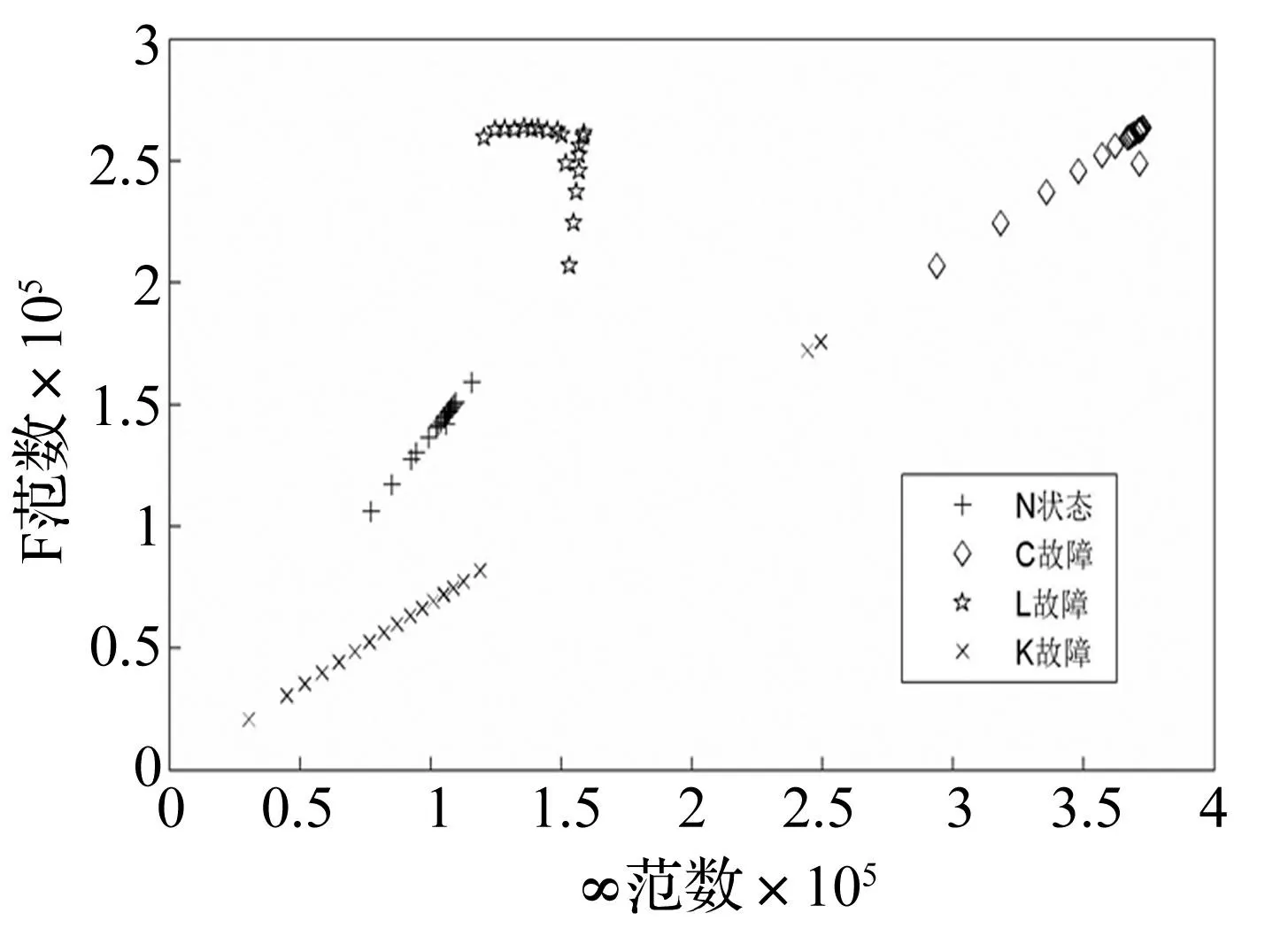
图4　特征参数的降维 Fig.4 Dimension reduction of the characteristic parameters

6结论

(1)本文提出了使用协整系数矩阵作为故障诊断的特征参数，以支持向量机作为分类方法，总结了应用协整系数矩阵进行故障诊断方法的一般步骤，为诊断系统故障提供了一种新的方法，并且在理论和仿真试验中证明了其可行性，试验结果表明，这种方法能将液压舵面仿真系统的各种状态较明显地进行故障诊断，有着很好的分类效果。

(2)本文在现有应用协整理论状态监测的基础上，进一步完善协整理论用于故障诊断的方法。对于非平稳的机械系统，提出了一种新的故障特征参数，相对传统方法，具有结构简洁，可以同时监测多个系统变量，损失系统动态信息少等优点，说明了协整理论在系统故障诊断领域具有广泛的应用前景。

参考文献

[1]陈前.关于工程大系统的状态监测与故障诊断[J].振动、测试与诊断，2002， 22(3):163-230.

CHENQian.Conditionmonitoringandfaultdiagnosisoflarge-scaleengineeringsystem[J].JournalofVibrationMeasurementandDiagnosis， 2002， 22(3):163-230.

[2]何正嘉，訾艳阳，孟庆丰,等.机械设备非平稳信号的故障诊断原理及应用[M].北京:高等教育出版社，2001：1-27.

[3]陈前，潘昱昱.协整理论应用于非平稳FCCU系统的状态监测与故障诊断[J].石油学报(石油加工)， 2007，23(1):69-76.

CHENQian，PANYu-yu.Applicationofcointegrationtestingmethodtoconditioningmonitoringandfaultdiagnosisofnon-stationaryFCCUsystem[J].ACTAPetroletSinica(petroleumprocessingsection)，2007，23(1):69-76.

[4]潘昱昱，陈前.协整理论在系统状态监测与故障诊断的应用研究[J]. 计算机测量与控制， 2006(3):281-284.

PANYu-yu，CHENQian.Monitoringandfaultdiagnosisofsystemusingmethodofcointegrationtest[J].ComputerMeasurementandControl， 2006(3):281-284.

[5]鲁帆，陈前. 液压系统组合协整模型状态监测[J]. 振动、测试与诊断，2011，31(4):409-414.

LUFan，CHENQian，Conditionmonitoringofhydraulicflapservosystemsusingsynthesiscointegrationmodel[J].JournalofVibrationMeasurementandDiagnosis，2011，31(4):409-414.

[6]CrossEJ，WordenK，ChenQ.Cointegration:anovelapproachfortheremovalofenvironmentaltrendsinstructuralhealthmonitoringdata[J].ProceedingsofRoyalSocietyA， 2011, 467(2133):2712-2732.

[7]DaoPB，StaszewskiWJ，CointegrationapproachfortemperatureeffectcompensationinLamb-wave-baseddamagedetection[J].SmartMaterialsandStructure， 2013，22(9):1-20.

[8]李子奈，叶阿忠.高等计量经济学[M].北京:清华大学出版社，2000：51-60，277-282.

[9]张世英，樊智.协整理论与波动模型[M].北京:清华大学出版社，2004：85-133.

[10]DickeyDA，FullerWA.Likelihoodratiostatisticsforautoregressivetimeserieswithaunitroot[J].Econometrica，1981， 49:1057-1072.

[11]Osterwald-Lenum，Michael，Anotewithquantilesoftheasymptoticdistributionofthemaximumlikelihoodcointegrationrankteststatistics[J].OxfordBulletinofEconomicsandStatistics， 1992， 54: 461-472.

[12]胡良谋，曹克强，徐浩军,等.支持向量机故障诊断及控制技术[M].北京:国防工业出版社，2011:23-27，35-57.

[13]王雷.支持向量机在汽轮机状态监测中的应用[M].北京:北京师范大学出版社，2012:25-48，123-153.

[14]TheodoridisS，KoutroumbasK.Patternrecognition[M].Elsevier，2004:61-99.

[15]CrossEJ,WordenK.ApproachestononlinearcointegrationwithaviewtowardsapplicationsinSHM[C]//JournalofPhysics:ConferenceSeries.IOPPublishing, 2011, 305(1): 012069.

[16]鲁帆，基于协整理论的复杂动态工程系统状态监测方法应用研究[D]. 南京:南京航空航天大学，2011.

第一作者张永亮男，博士生，1984年生

通信作者孟秀云女，博士，教授，博士生导师，1964年生