列车白车身损耗因子试验研究

第一作者欧阳山男，博士生，1985年生

通信作者隋富生男，研究员，1970年生

列车白车身损耗因子试验研究

欧阳山1,2，鲁帆2，伍先俊2，隋富生2

(1.中国科学院大学，北京100190；2.中国科学院声学研究所噪声与振动重点实验室，北京100190)

摘要：对7 m长高铁车厢白车身划分子系统，根据能量平衡方程确立子系统总损耗因子、内损耗因子和耦合损耗因子的关系，通过测量总损耗因子和能量比可以直接计算内损耗因子和耦合损耗因子。为了准确测量总损耗因子，计算中采用Hilbert变换求瞬态信号对数衰减率的方法，其创新点在于不需要测量输入功率就可以得到完整方程并获得统计能量分析参数。内损耗因子和耦合损耗因子的计算结果可以为建立车厢能量统计模型提供数据参考。

关键词：白车身；统计能量分析；总损耗因子；内损耗因子；耦合损耗因子；Hilbert变换

基金项目：国家973计划(2013CB632900);国家863计划(2011AA11A103)资助项目

收稿日期：2014-01-26修改稿收到日期：2014-03-27

中图分类号:TB535.1;U271.91文献标志码：A

Experimental study on loss factors for train carriage body in white

OUYANGShan1,2，LUFan2,WUXian-jun2,SUIFu-sheng2(1. University of Chinese Academy of Sciences, Beijing 100190, China;2. Key Laboratory of Noise and Vibration Research, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China)

Abstract:The train carriage body in white (BIW), with the length of 7 meters, was divided into 6 subsystems. Based on the energy balance equation, the interrelation among total loss factor, internal loss factor and coupling loss factor of subsystems was determined. Internal loss factor and coupling loss factor can be calculated by using experimental results of total loss factor and the energy ratio. In order to improve the accuracy of experimental results of total loss factor, a method of Hilbert transform, without need of measuring input power, was introduced to calculate the logarithmic decrement of transient response. The results of loss factors can be used for building up the statistical energy analysis(SEA) model of high speed railway carriage.

Key words:body in white (BIW); statistical energy analysis(SEA); total loss factor; internal loss factor; coupling loss factor; Hilbert transform

采用仿真分析方法研究大型结构的动力学性能问题、结构减振降噪预设计问题是一种简便有效的手段，根据分析频带的侧重点可以采用低频有限元分析或者中高频统计能量分析。无论是有限元分析还是统计能量分析，建立准确的结构模型是必要前提。对统计能量模型而言，除了合理划分子系统外，最重要的参数就是子系统间内损耗因子和耦合损耗因子。装配体部件内损耗因子包含结构损耗因子、边界损耗因子和声辐射损耗因子。同一种材料组成的不同形式的结构部件，内损耗因子一般是不一样的，而耦合损耗因子不仅和结构形式有关，还跟结构装配形式密切相关，因而针对不同的装配系统都需要获取相应的损耗因子。

确定损耗因子的方法可以通过理论计算[1]、有限元建模分析[2]和实验方法得到。由于高铁车厢白车身尺寸大、结构复杂，理论计算是不可实现的，而在宽频范围内通过有限元分析获取损耗因子的方法则耗时耗力，因为有限元分析本身需要准确的结构模型，其准确性验证仍然需要实验得到模态参数。白车身子系统损耗因子的有效识别方法是实验测试。

实验获取内损耗因子的经典方法是功率输入法和瞬态衰减法，Bies等[3-4]研究了功率输入法获取内损耗因子和耦合损耗因子的问题，张宏亮等[5]研究发现该方法在低频范围不准确。在实际应用中，功率输入法有很大的局限性。该方法一般以激振器作为激励源对子系统注入稳态随机激励，但对如车厢侧壁及车顶等非靠近地面的子系统，激振器难以安装，因而该方法不可用。瞬态衰减法测内损耗因子受到许多研究者的青睐[5-10]，但是该方法要求子系统与其他子系统分离，当复杂结构子系统之间装配在一起且不可分离时，内损耗因子无法通过该方法直接获得。耦合损耗因子一般通过计算得到，对于简单的点、线连接结构，有相应的理论计算公式[11]，复杂结构耦合损耗因子只能通过能量平衡方程计算得到[12]。对已经装配好、难以直接获取内损耗因子和耦合损耗因子的结构，孙进才[13]提出改进的方法，即通过测试子系统总损耗因子，根据总损耗因子和内损耗因子的关系求出内损耗因子，进而由内损耗因子和耦合损耗因子的关系计算耦合损耗因子。然而该方法在计算内损耗因子的能量平衡方程中忽略了非保守耦合因素的影响，没有考虑子系统间的非保守耦合损耗效应，对复杂系统的内损耗因子计算有失全面。

针对复杂的火车车厢装配系统，以上的测试方法难以适用，本文采用另一种思路，即直接从原始能量平衡方程出发，得到子系统总损耗因子和内损耗因子以及耦合损耗因子的关系式，通过测量白车身子系统总损耗因子以及子系统间的能量比，直接求出内损耗因子和耦合损耗因子。该方法在满足子系统能量平均分布的假设下没有作任何的条件简化，因而计算结果更加合理。该方法的关键在于准确的测量总损耗因子和子系统能量，本文采用基于Hilbert变换的方法测量总损耗因子。

1理论基础

1.1总损耗因子

装配体的某个子系统受到脉冲激励时，会产生随时间迅速衰减的振动信号，该衰减信号是子系统自身损耗和相邻子系统间损耗的综合作用结果。单位激励加速度响应信号可以表示为：

(1)

式中:ηt是总损耗因子，它等于单位圆频率输入功率和受激子系统的能量之比：

(2)

由于损耗因子ηt一般和频率有关，在宽频带范围，没有必要得到每个频率的损耗因子ηt。宽频带分析振动和噪声一般采用1/3倍频程频域，因而可以只计算1/3倍频程中心频率处的ηt。假设响应信号经过中心频率为ωn，带宽为ωd的带通滤波器滤波后，响应信号变为[12]：

(3)

式中:A是幅值，ηs是带宽内总损耗因子。对信号滤波可以采用巴特沃斯带通滤波器，选择合适的阶数可以获得较好的结果。下面给出通过Hilbert变换求信号包络，进而计算中心频率处总损耗因子ηs的方法。

滤波后信号an(t)的Hilbert变换表示为[10]：

(4)

响应信号的解析信号为：

(5)

解析信号的幅值A(t)就是响应信号的包络，表示为：

(6)

将包络取对数得到衰减曲线，由衰减曲线可识别出对数衰减率δ，进而得到损耗因子ηs：

(7)

(8)

本文通过图1展示了计算1/3倍频程1 000 Hz总损耗因子的过程，其中滤波信号的对数包络经常出现衰减快和衰减慢的斜率。有研究指出[5-6]衰减率应取衰减较快的初始斜率1作为对数衰减率，本文直接通过观察原始信号迅速衰减的时间段选取衰减快的斜率进行计算。

图1　响应信号求对数包络衰减率过程 Fig.1 The procedure example for identifying logarithmic decrement of signal envelope

1.2内损耗因子和耦合损耗因子计算

统计能量分析要求子系统满足能量平均的假定，在定量上要求分析频带内模态数Nf≥5。在满足该要求的情况下，根据SEA传统理论，当由N个子系统装配的耦合系统中子系统m有输入功率Pm时，有能量平衡方程[13]：

m=1,…,N

(9)

i=1,…,N且i≠m

(10)

将式(9),(10)两边分别除以ωEm，得到总损耗因子、内损耗因子、耦合损耗因子的关系式：

m=1,…,N

(11)

i=1,…,N且i≠m

(12)

式中:Ei，i=1,2,…,N表示的是子系统的时空平均振动能量。假设子系统j有M个响应点，子系统i有N个激励点，依次在子系统i的N个位置上激励，得到子系统j的时空均方速度为：

(13)

Θs=ΕΘ

(14)

式中:Θs=[ηs1,0,ηs2,0,ηs3,0,ηs4,0,ηs5,0,ηs6,0]T，

Θ=[η11,…,η16,η21,…,η26,…,η61,…,η66]T，Θs中0分量为0=[0,0,0,0,0]；Ε为由相应能量比组成的36×36矩阵。由此得到内损耗因子和耦合损耗因子组成的向量

Θ=Ε-1Θs

(15)

由测试获得的总损耗因子ηsm和平均能量Ej，根据式(11),式(12)可计算内损耗因子和耦合损耗因子。

2实验模型

从一节高铁车厢骨架中截取靠近车门的7 m作为白车身模型，在截断面上安装车门，形成一个“完整”的模型，模型如图2所示。白车身置于半消声室，底部用橡胶弹簧支撑。为了研究铝型材车体自身的振动能量耗散特性，车体未安装玻璃和封闭门。由于白车身结构非常复杂，车厢底板外侧包含大量的梁结构，车端门筋、梁、板混合，在实际建立统计能量计算模型时，需充分考虑壁面与壁面之间以及壁面内各种梁之间的连接关系，合理划分子系统。子系统划分得越精细，所需获取的损耗因子参数就越多，这对实验测试本身就是一大挑战。本文的侧重点不是测试所有连接部件的损耗因子，而是集中于研究车底、车顶、侧墙、车门大块完整部件之间的能量流传递特性，因而只考虑大块板之间内损耗和耦合损耗。根据车体结构大板块装配的特点，可以将车厢划分为截断门、左右侧壁、车顶、车底6个子系统，如图3所示。

图2　白车身实验模型 Fig.2 Experimental model of the carriage BIW

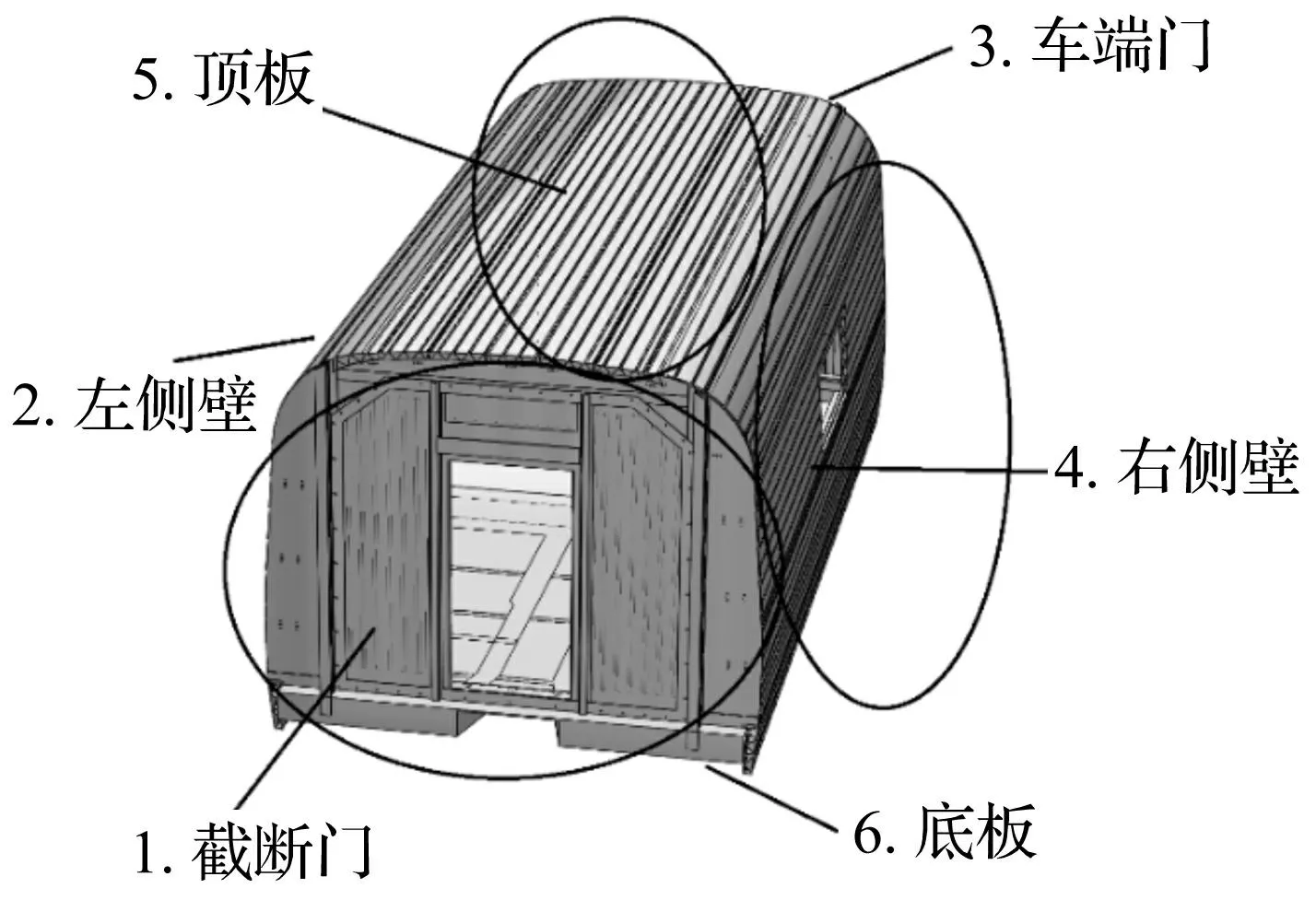
图3　白车身子系统划分示意图 Fig.3 Subsystem division of the carriage BIW

实验需得到子系统总损耗因子和平均能量。对于小型简单结构，子系统平均能量可以通过一次性布置足够数量的加速度计和少量激励点得到；但对于大型装配系统，一般来说缺乏足够的加速度计一次性布满所有的子系统。这种情况下平均能量可以通过增加激励点、减少响应点的方法获取。该方法具体描述为在子系统的非振动节点位置布置M个(少量)加速度测点，而在子系统其他区域均匀分配N个(N远大于M)激励点，通过力锤分别激励各个激励点，可以获得足够的速度响应信息，由此得到平均振动能量。

图4　侧壁加速度计测点分布示意图 Fig.4 Positions of accelerometers on the flank side of the carriage

本文采用这种简便的方法，在车厢内的每个面布置25个力锤激励点和8个加速度响应点，获取传递函数作为单位激励响应，有效带宽0-3 200 Hz。测点的布置根据子系统的具体形式而有所调整，以侧壁子系统为例，8个加速度测点分布如图4，而25个力锤激点平均分布在侧壁其余位置。其中，力锤激振方向和加速度计拾振方向均为所在面板的法向。如此即可以保证侧壁被充分激励，又能得到平均意义上的振动速度。每完成一个面的激励，每个子系统都将得到25×8的单位响应，通过式(13)计算均方速度，便可得到6个子系统的平均能量。在测量总损耗因子时，在激励面上选取离激励点最近的响应点时域信号进行分析，计算多个激励点响应信号的总损耗因子，求平均值作为该子系统的总损耗因子，从而获得较准确的结果。

3结果分析

3.1能量比

测试中分别敲击车厢内6个子系统，每激励一个

子系统可获得所有子系统的振动能量，以被激励的子系统振动能量为参考，则可以得到其他子系统与参考子系统的能量比。敲击不同子系统时能量比见图5。

图5中曲线标记Eij=Ei/Ej表示无激励子系统与受激励子系统能量比。从能量比曲线来看，在分析频段范围内，基本上是无源子系统能量小于有源子系统的能量，即能量从有源结构传递到无源结构，从而形成整体振动。但是在特定情况下，无源子系统振动能量接近甚至大于有源子系统能量。激励质量大的子系统如左、右侧壁以及顶板、底板时(见图5(a)-(d))，在50 Hz-100 Hz范围内无源子系统与有源子系统能量比较接近，甚至超过有源子系统能量，而激励质量小的子系统时能量比远小于1(见图5(e) (f))。出现这种现象说明在50 Hz-100 Hz范围内，激励质量大的子系统容易引起整个系统的全局共振，使得各子系统间能量较均衡，而低频共振模态分布的差异导致个别无源子系统能量大于有源子系统。由此产生的结果是，相关频率范围内，式(14)的矩阵方程中能量比系数矩阵非对角线元素接近或者大于对角线元素，从而耦合损耗因子计算结果可能比内损耗因子大，甚至出现负值。因而在计算损耗因子时100 Hz以下的结果可靠性值得怀疑，本文3.3节将从频带模态数角度进一步验证。

3.2总损耗因子

各子系统总损耗因子见图6。

图5　激励不同子系统时的能量比 Fig.5 Curves of the energy ratio of subsystems

图6　铝型材车体各子系统总损耗因子 Fig.6 Curves of total loss factor of 6 subsystems

图中显示，各壁面总损耗因子大小比较接近，变化趋势也一样。模态测试结果表明，车厢结构前6-7阶整体弯曲模态出现在10 Hz-100 Hz，该频段受脉冲激励时容易引起整体共振，总的能量传播/耗散能力较强。因而100Hz以下，总损耗因子较大，随频率变化小，基本上在0.1范围内；100 Hz以上，总损耗因子随着频率增加而逐渐衰减，3 000 Hz总损耗因子约为5×10-3。

3.3内损耗因子

3.1节和3.2节分析能量比和总损耗因子时分析频带为8 Hz-3 200 Hz，几乎涵盖了测试全部有效带宽范围，由于计算结果是直接从测试数据得到的，因而有效性可以保证。然而内损耗因子和耦合损耗因子需要通过式(11),式(12)求得，其计算频率范围需要满足带宽内模态数Nf≥5的条件。在激振器随机激励下得到白车身各壁面测点的传递函数，导入模态分析软件ME’scopeVES进行模态分析，通过模态计数法识别出1/3倍频程250 Hz以下的模态数，中心频率表示的模态数见表1。

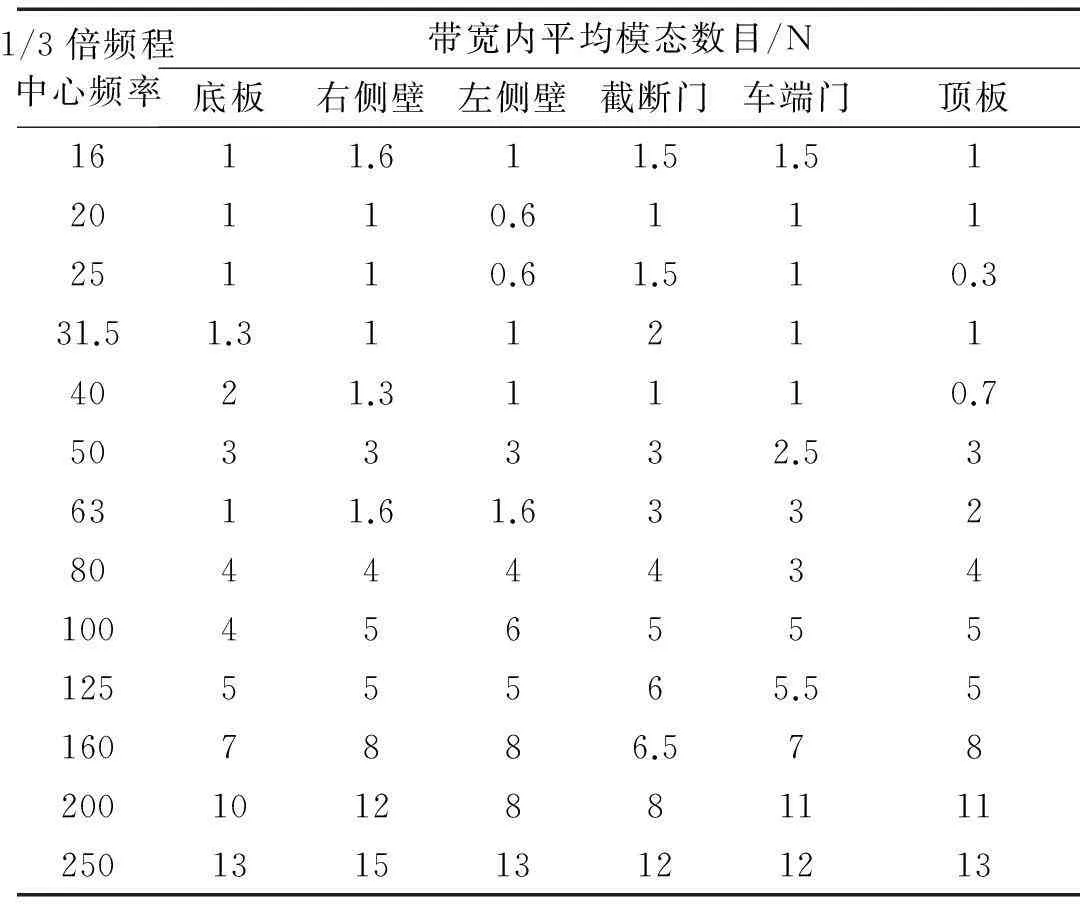
表1　车厢白车身250 Hz以内各子结构模态数

表1中显示在100 Hz以上带宽内模态数满足 的条件，因此通过式(11),式(12)计算内损耗因子应在100 Hz以上才较可靠。

车厢骨架结构有6个子系统，根据式(11),式(12)，脉冲激励每个子系统都会产生6个方程，激励6个子系统将产生36个方程，写成矩阵方程的形式就是式(14)，再由3.1节和3.2节计算的总损耗因子和能量比，可得到内损耗因子和耦合损耗因子。各子系统100 Hz以上内损耗因子如图7所示。

图7　白车身各子系统内损耗因子 Fig.7 Internal loss factor of different subsystems

图7显示车端门和底板内损耗因子η3、η6大小接近，在800 Hz-1 000 Hz内数值最小，接近0.001。其他子系统内损耗因子随频率增加逐渐降低，但数值一般在0.004以上。子系统内损耗因子远比铝材料的结构损耗因子10-4大，这是因为子系统装配形式复杂，装配体形成的空腔混响效果明显，声辐射损耗和边界损耗效应远大于结构损耗，因而产生较大的内损耗因子。

3.4耦合损耗因子

耦合损耗因子随频率的变化比较复杂， 100 Hz以上耦合损耗因子变化曲线见图8。从曲线看出，耦合损耗因子在500 Hz以内数值较大，跟内损耗因子在同一数量级，表明该频段子系统间功率流传递能力非常强。500 Hz以上所有耦合损耗因子基本很小，在10-6~2×10-4范围内，比内损耗因子小得多，这是符合统计能量法在工程应用中的测量经验的。图8可以看出车厢结构是非保守耦合结构，从耦合损耗因子来看，ηij≠ηji。

4结论

直接利用能量平衡方程得到子系统总损耗因子、内损耗因子和耦合损耗因子的关系，通过测量总损耗因子和能量比直接计算内损耗因子和耦合损耗因子。该方法的优点是无需做任何条件简化，计算结果能更全面反应子系统的损耗特性。不足之处是方程数多，能量比系数矩阵大，编写程序较繁琐。

图8　各子系统与相邻子系统间耦合损耗因子 Fig 8. Coupling loss factors between adjacent subsystems

由于车厢装配体结构复杂，车厢子系统之间耦合损耗因子尚无公开的测试数据，因而本文的实验研究对此作出初步探讨。从结果分析来看，由铝型材组成的车身各个子系统内损耗因子基本在0.004以上，远大于结构损耗因子，表明声辐射损耗和边界损耗效应远大于结构损耗，此结论和实验现场(半消声室)中车厢内混响效应明显以及车身装配边界复杂繁多的现象是一致的。耦合损耗因子在500 Hz以下数值接近内损耗因子，子系统间功率流传递能力非常强；500 Hz以上数值远小于内损耗因子，满足实际的能量传递/耗散情况。本文的损耗因子参数测试结果可以为车厢白车身统计能量建模分析提供参考。

参考文献

[1]Lyon R H, DeJong R G, Heckl M. Theory and application of statistical energy analysis[J]. The Journal of the Acoustical Society of America, 1995, 98(6): 3021-3021.

[2]Maxit L, Guyader J L. Estimation of SEA coupling loss factors using a dual formulation and FEM modal information[J]. part I: theory. J Sound Vib, 2001, 239(5): 907-930.

[3]Bies D A, Hamid S. determination of loss and coupling loss factors by the power injection method[J]. J Sound Vib, 1980, 70(2): 187-204.

[4]Liu W, Ewing M S. Experimental and Analytical Estimation of Loss Factors by the Power Input Method[J]. AIAA Journal, 2007, 45(2): 477-484.

[5]张红亮, 孔宪仁, 刘源等. 宽频域的内损耗因子实验辨识方法研究. 振动与冲击[J]. 2013, 32(12): 179-184.

ZHANG Hong-liang, KONG Xian-ren, LIU Yuan,et al. Test identification of damping loss factor in a wider frequency range[J]. Journal of Vibration and Shock,2013, 32(12):179-184.

[6]Wu L, Agren A. Analysis of initial decay rate in relation to estimates of loss factor and equivalent mass in experimental SEA[J]. ISMA 21, 1996: 187-198.

[7]Bloss B C, Rao M D. Estimation of frequency-averaged loss factors by the power injection and the impulse response decay methods[J]. The Journal of the Acoustical Society of America,2005,117: 240-249.

[8]Cabell R, Schiller N, Allen A, et al. Loss factor estimation using the impulse response decay method on a stiffened structure [C]. Inter-Noise 2009, Ottawa, Canada, 2009.

[9]毛伯永, 谢石林, 张希农. 冲击载荷识别的瞬态统计能量分析方法[J]. 振动与冲击, 2013, 32(14): 46-51.

MAO Bo-yong, XIE Shi-lin, ZHANG Xi-nong. Identification of impact load based on transient statistical energy analysis method[J]. Journal of Vibration and Shock, 2013, 32(14): 46-51.

[10]程广利, 关成彬, 胡生亮. 基于 Hilbert 变换的结构内损耗因子测试研究[J]. 噪声与振动控制, 2006, 26(4): 105-107.

CHENG Guang-li, GUAN Cheng-bin, HU Sheng-liang. Study on the Measurement of Structure’s Internal Loss Factor based on Hilbert Transform[J]. Noise and Vibration Copntrol,2006, 26(4): 105-107.

[11]明瑞森, 孙进才. 非保守耦合结构间耦合损耗因子的计算[J]. 西北工业大学学报, 1989, 7(1): 39-46.

MING Rui-sen, SUN Jin-cai. Calculation of coupling loss factor of non-conservatively coupled structures[J]. Journal of Northwestern Polytechnical University, 1989, 7(1): 39-46.

[12]姚德源, 王其政. 统计能量分析原理及其应用[M]. 北京:北京理工大学出版社, 1995.

[13]孙进才. 复杂结构的损耗因子和耦合损耗因子的测量方法. 声学学报[J]. 1995, 20(2): 127-134.

SUN Jin-cai. Measuring method of dissipation and coupling loss factors for complex structures[J]. Acta Acustica, 1995, 20(2): 127-134.