空间站柔性太阳翼热诱发振动分析

第一作者孔祥宏男，博士生，1986年1月生

空间站柔性太阳翼热诱发振动分析

孔祥宏，王志瑾

(南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京210016)

摘要：柔性太阳翼随空间站在轨运行时会受到周期性的热载荷作用，为研究热载荷对柔性太阳翼的影响，采用热-结构非耦合分析方法对柔性太阳翼进行了热诱发振动分析。提出了等效位移法，按照节点位移等效原则计算柔性太阳翼有限元模型各节点的等效温度载荷，再以该载荷为激励计算柔性太阳翼的动态响应。通过自编的Python程序实现等效温度载荷计算过程中的数据处理，以及热诱发振动分析流程中的有限元前后处理。通过与理论解和数值解作对比，验证了基于等效位移法求解等效温度载荷并用于非耦合热诱发振动分析的方法的准确性。通过对柔性太阳翼的热诱发振动分析，得到了柔性太阳翼的动态响应数据，发现了柔性太阳翼出地球阴影区时的刚柔耦合情况。分析结果可以为柔性太阳翼的设计和改进以及在轨的安全性、可靠性的评估提供参考。

关键词：柔性太阳翼；热诱发振动；位移等效原则；等效温度载荷；刚柔耦合

基金项目：江苏高校优势学科建设工程资助项目

收稿日期：2014-01-08修改稿收到日期：2014-03-07

中图分类号:V415.4文献标志码：A

Thermally induced vibration analysis of a space station’s flexible solar wing

KONGXiang-hong,WANGZhi-jin(Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:A flexible solar wing(FSW) suffers from periodic thermal load when running on orbit together with a space station. In order to investigate the effect of thermal load on FSW, an uncoupled thermal-structural analysis method was introduced to perform the thermally induced vibration analysis(TIVA) of FSW. The finite element(FE) method and the equivalent displacement principle of nodes were used to calculate equivalent temperature loads(ETLs) on nodes of the FSW’s model and then to calculate the dynamic response of FSW under ETLs. A self-compiled Python program was provided to process the data of the ETLs calculation and complete the FE pre-and post-processing for TIVA. Comparing the theoretic results with the numerical ones, it was shown that the TIVA method is accurate; with TIVA, the dynamic response of FSW is gotten, and the rigid-flexible coupling phenomenon of FSW is found out; the results of TIVA can offer a reference for the design and improvement of FSW, and can also be used to assess the security and reliability of FSW.

Key words:flexible solar wing; thermally induced vibration; equivalent displacement principle; equivalent temperature load; rigid-flexible coupling

空间站在轨运行期间，会周期性地进出地球阴影区和日照区，在太阳辐射、地球反照等热载荷的作用下，空间站外露无热防护的部件的温度会周期性地变化。部件的温度变化会引起热变形，甚至引发振动。

热诱发振动问题的研究始于Boley[1]，他对梁由突加热载荷引起的振动进行了研究。Manolis[2]等提出了一种数值方法用于研究突变热载荷引起的梁结构的动响应。Seibert 等[3]采用热弹耦合方法对梁的热诱发振动进行了研究。Kidawa-Kukla[4]应用格林函数研究梁的热诱发振动，对移动热源引发的梁的横向振动进行了研究。Wattanasakulpong等[5]使用源自弹性理论的改进的三阶剪切变形理论对功能梯度梁进行了线性热屈曲和振动分析。Shen等[6]使用绝对节点坐标方程对柔性梁进行了热-结构耦合分析，得到了与Boley(1956)非常相近的热诱发振动的计算结果。孙良新等[7-13]等对复合材料层压板进行了热诱发振动研究。

随着航天技术的发展，为了保证航天器在空间环境中安全运行，对航天器进行空间环境条件下的热分析和热诱发振动分析显得尤为重要。徐向华等[14]对近地轨道航天器进行了热辐射分析，李鹏等[15-17]对航天器太阳翼进行了在轨热分析。姚海民等[18-24]对航天器的热应力、热诱发振动等进行了研究。

空间站柔性太阳翼结构复杂，柔性阵面与刚性支撑结构的力学、热学性能差别较大。鉴于空间复杂环境，在太阳翼设计过程中必须要考虑太阳翼的热变形及可能发生的热振动，再根据热分析、热振分析的结果改进设计。热诱发振动分析的方法通常有热-结构耦合[3, 21-22]和非耦合[7, 12, 18, 20, 23 ]的方法。一般情况下，热-结构耦合方法得到的动响应非常接近非耦合方法得到的动响应[3]。但是，当热变形造成的阳光入射角变化较大时，热-结构耦合对温度和位移造成的影响不容忽略[22]。

理论解析方法难以对包含材料非线性、几何非线性的大型柔性太阳翼进行热-结构耦合分析。鉴于太阳翼热变形引起的阳光入射角变化较小及现有商用有限元软件具有的分析功能，本文采用热-结构非耦合的方法研究空间站柔性太阳翼在轨一个周期内的热变形及热诱发振动。

1非耦合热诱发振动基本理论

非耦合热诱发振动分析方法忽略结构的热变形对温度场分布的影响，通过对结构温度场的计算得到等效温度载荷，再以等效温度载荷作为激励，对结构进行动响应分析。由于当结构的温度发生变化时，结构会发生相应的热变形，等效温度载荷是指这样一种力或力矩，结构在该力或力矩的作用下发生的变形与在温度变化作用下发生的热变形相同。

1.1热传导公式及温度场的计算

非耦合热诱发振动分析的第一步是求解结构随时间变化的温度场，在不考虑热变形的情况下，热传导微分方程可写为：

(1)

式中:温度T(x,y,z,t)是位置坐标和时间t的函数，W(x,y,z,t)为热源强度，导温系数a=k/cρ，c为比热容，ρ为密度，k为导热系数。

黄后学等[17]使用I-DEAS软件对刚性太阳翼进行了在轨热分析，得到了不同工况的太阳翼温度场。本文在柔性太阳翼热诱发振动分析中所使用的太阳翼的温度数据同样由I-DEAS软件根据空间站的轨道参数和太阳翼的姿态计算得到。

1.2热应变公式及等效温度载荷的计算

弹性体温度的变化会引起体积的变化，即热膨胀。在边界条件或其他约束的作用下会产生热应力。在计算等效温度载荷时，主要关心热应变。

物体由于热膨胀只产生线应变，而不产生剪切应变，因此对于各向同性材料，温度变化T时，由于自由膨胀引起的各方向的正应变为aT，而切应变为零，即：

εx=εy=εz=aT，γxy=γyz=γzx=0

(2)

使用有限元方法可以计算模型中各单元各节点的等效温度载荷的各个分量。由热应变引起的等效温度载荷可表示为：

(3)

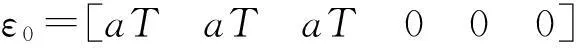
1.3动力学基本理论

动力学有限元方法的系统求解方程为：

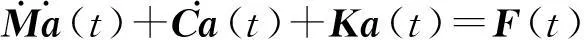
(4)

非耦合热诱发振动的系统求解方程仅需将式(4)中的节点载荷向量F(t)替换为随时间变化的节点的等效温度载荷向量Pε0(t)，即：

(5)

将使用等效位移法计算得到的等效温度载荷作为激励加载到振动模型上，即可得到模型的动响应。

1.4非耦合热诱发振动分析流程

非耦合热诱发振动分析的整个分析流程可分为四步：

热分析——求解太阳翼在轨一个周期内各部件的温度变化，得到各节点的温度-时间数据T(t)；

温度-位移耦合分析——以热分析得到的各节点的温度-时间数据作为载荷，计算太阳翼的准静态热变形，得到各节点的位移-时间数据u(t)；

静力分析——以温度-位移耦合分析得到的各节点的位移-时间数据为位移载荷，计算各节点随时间变化的支反力，得到支反力-时间数据RF(t)。

动力学分析——以静力分析得到的各节点的支反力-时间数据作为激励，计算有限元模型的动态响应。

热分析使用I-DEAS软件完成，其余三步分析使用Abaqus软件完成。由于太阳翼结构中阵面与桅杆的固有频率相差很大，无法采用基于模态的振型叠加法求解太阳翼的动态响应，因此对太阳翼的动态响应分析采用隐式动力学分析方法。由于太阳翼有限元模型的单元、节点数量较多，在分析流程中的数据处理量较大，因此使用Python语言编写了用于Abaqus前后处理的程序，可以准确、高效地读取前一步的分析数据，在后一步分析的模型上加载位移、力等载荷。

1.5等效温度载荷的有限元计算方法

对于大型复杂结构，使用式(3)所示的有限元方法求解有限元模型各节点的等效温度载荷难度非常大，因此，本文提出一种基于等效位移的方法求解等效温度载荷，使用温度-位移耦合分析、静力分析将热分析得到的节点温度T(t)转换为等效温度载荷Pε0(t)。

等效位移法假设有限元模型在所有节点的等效温度载荷(力或力矩)作用下的变形(或各节点的位移)与实际模型在热载荷作用下的变形相同。对于杆单元、体单元，节点的等效温度载荷为力；对于梁单元、壳单元，如果梁截面、壳厚度方向存在温度梯度，则梁单元、壳单元的节点的等效温度载荷为力和力矩。以模型的节点位移作为中间量，将温度载荷转化为等效的外力或力矩。

由于结构在热载荷作用下会发生热变形，因此，对于有限元模型来说，在一定热载荷作用下，各节点会有相应的位移，即由热变形引起的节点位移u(t)是节点温度T(t)的函数，可以写为：

u(t)=f(T(t))

(6)

以式(6)的节点位移u(t)作为位移载荷加载到有限元模型上进行静力分析，可以得到与节点位移u(t)各时刻对应的节点的支反力RF(t)，即RF(t)为u(t)的函数，可以写为：

RF(t)=g(u(t))

(7)

根据有限元理论可知，式(7)的理论依据为：

Ku=F

(8)

式中，K为有限元模型的刚度矩阵，u为节点位移向量，F为节点载荷向量。

对于柔性太阳翼等大型复杂结构，式(6)和式(7)所表达的函数关系使用热弹性力学、有限元方法等很难求解，因此可以使用商用有限元软件直接进行求解。

有限元模型除边界外的每个节点、每个时刻的支反力RF(t)即为该节点在相应时刻的等效温度载荷Pε0(t)，因此也就得到了所有节点的等效温度载荷-时间数据。

2算例验证

为验证本文所用的非耦合热诱发振动分析方法的正确性，使用与文献[7]相同几何参数、材料参数和热载荷的复合材料层压板进行了热诱发振动对比分析；采用在研的空间站柔性太阳翼桅杆与文献[21]中的太阳翼桅杆的热诱发振动分析结果进行了对比研究。

2.1复合材料层压板热诱发振动分析

使用文献[7]中25 cm×25 cm×0.5 cm的层压板，建立三维实体有限元模型如图1所示。按照文献[7]中所给温度突变载荷，对模型施加如式(9)所示的突变温度场。式(9)中节点(x,y,z)坐标为图1中所注原点位置的坐标系下的坐标。模型4个侧面中间位置的节点(图1右侧图中黑色方点)为简支约束。

ΔT(x,y,z)=100zsin(πx/25)sin(πy/25)

(9)

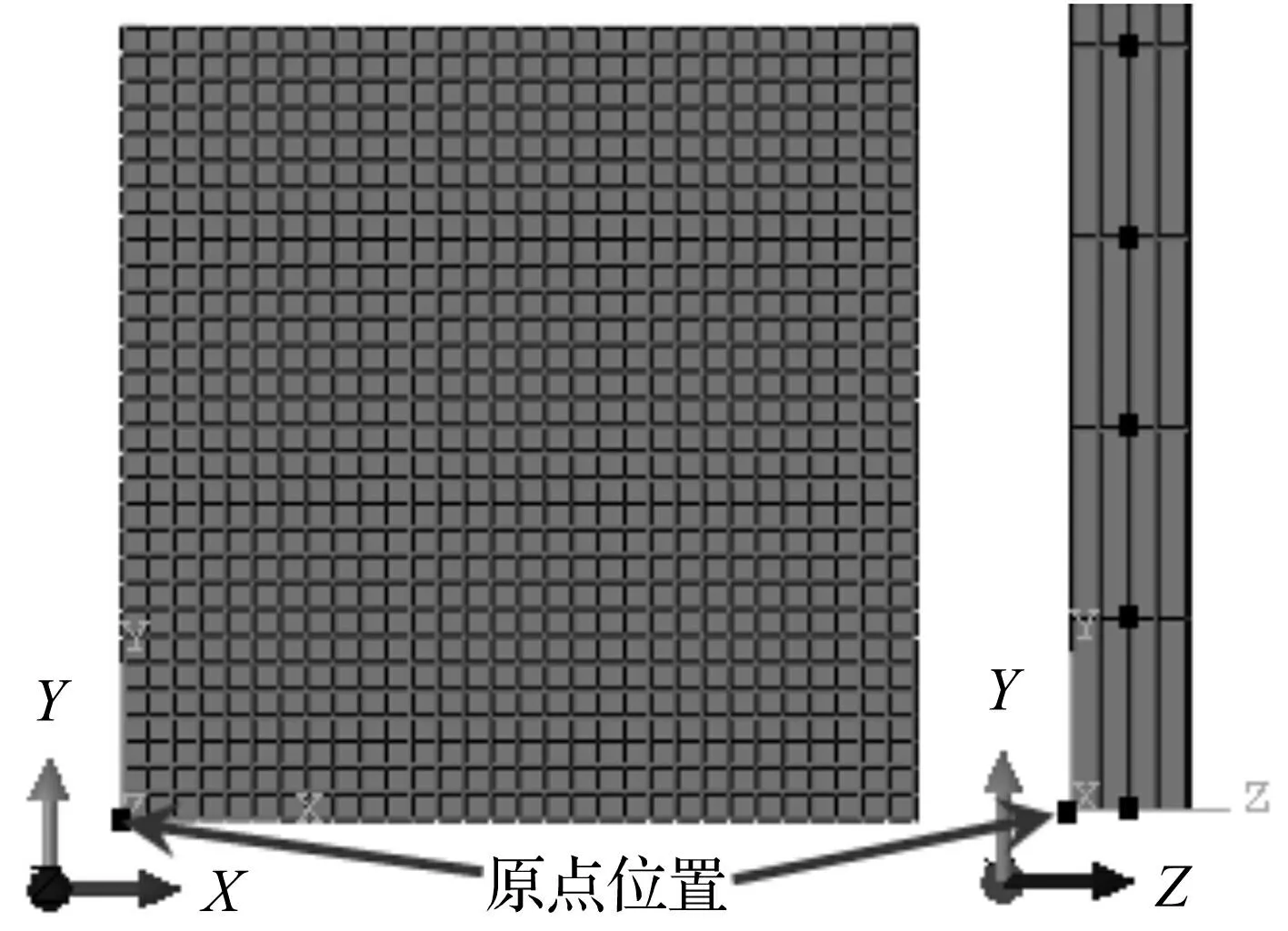
图1　复合材料层压板有限元模型 Fig.1 Finite element model of composite laminate

使用本文所述非耦合热诱发振动有限元分析方法得到的层压板上表面(z=0.5 cm)面心处节点沿面的法向的位移响应如图2所示，图2中的位移-时间曲线与文献[7]中图7几乎完全一致。由此证明，本文所述的非耦合热诱发振动分析方法及基于等效位移求解等效温度载荷的方法是正确、有效的。

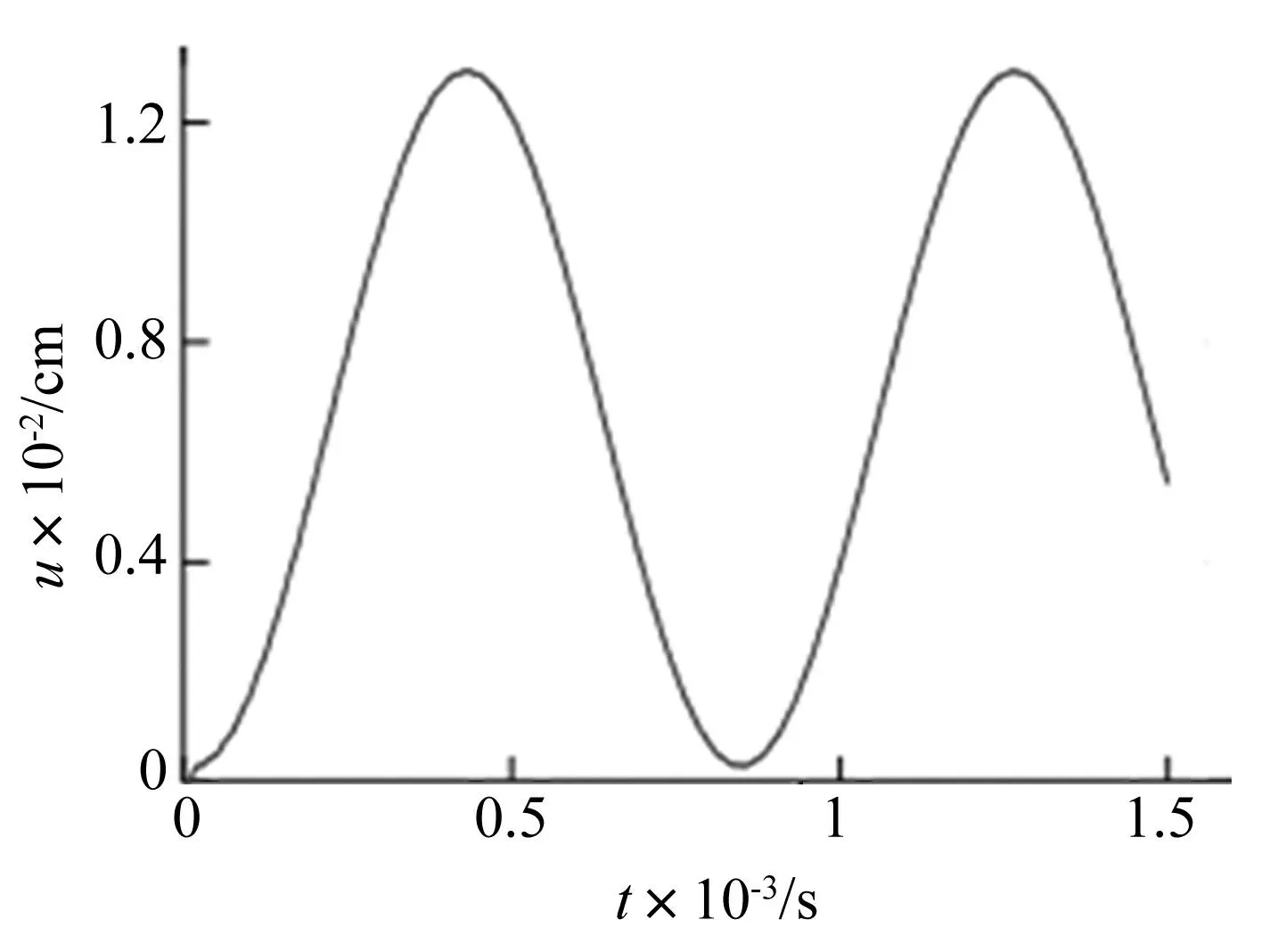
图2　层压板中点位移-时间曲线 Fig.2 Displacement-time curve of the laminate’s central point

2.2太阳翼桅杆热诱发振动分析

文献[21]使用了全区间耦合、单步内非耦合的有限元方法对空间站太阳翼桅杆进行了热诱发振动分析。计算所用的空间站柔性太阳翼桅杆的纵向尺寸和横向尺寸均为文献[21]中所用桅杆尺寸的两倍左右。本文采用非耦合方法对桅杆进行了热诱发振动分析，虽然本文计算的桅杆尺寸、工况与文献[21]不同，但得到了与文献[21]非常相似的结果。桅杆底端固支，顶端自由，图3为桅杆顶端有限元模型。图4所示为图3中桅杆顶端节点P1在两个轨道周期内的位移响应，图中U1、U2、U3分别为P1点在X轴、Y轴、Z轴的位移分量，U为位移标量。图4(b)为图4(a)中U3曲线初始300s的放大图。图4(a)、图4(b)分别与文献[21]的图11、图12的振动规律相似。

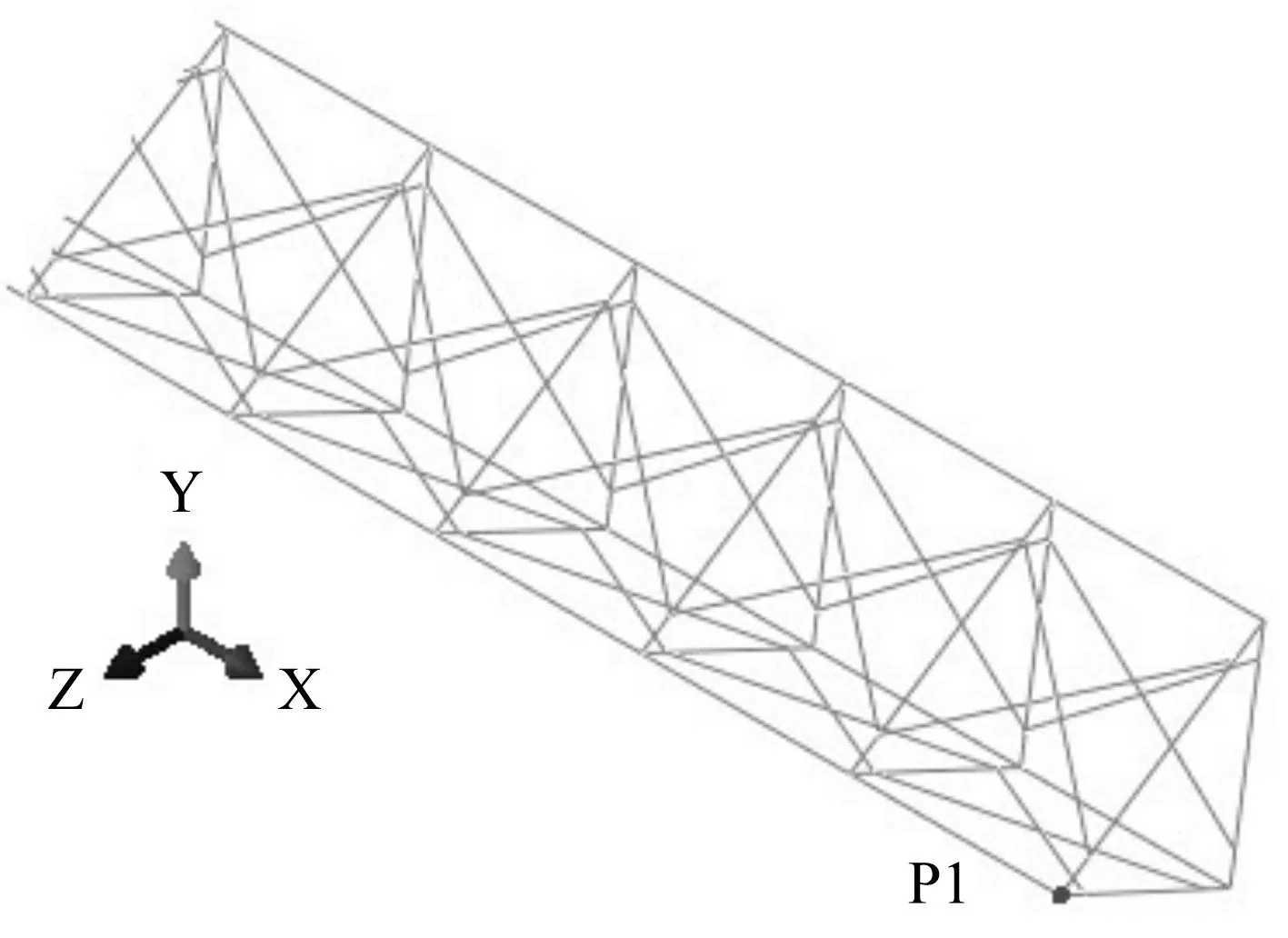
图3　太阳翼桅杆顶端局部有限元模型 Fig.3 Finite element model of top part of the solar wing’s mast

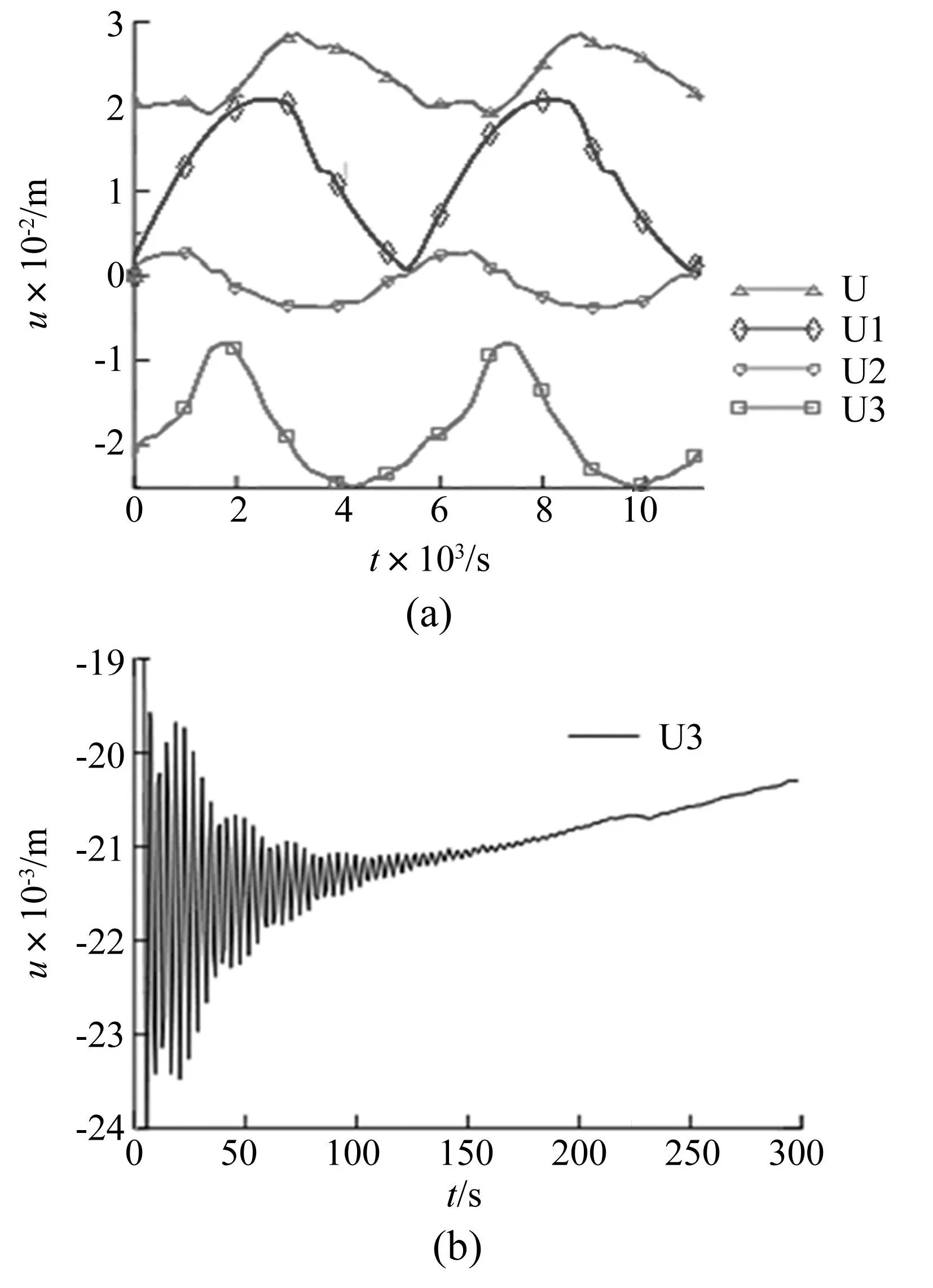
图4　桅杆顶端P1点位移响应 Fig.4 Displacement response of mast’s point P1

文献[21]认为：虽然中央桁架(即桅杆)在初始阶段发生了明显的热振动，但随着时间的推移将进入稳态强迫振动阶段，它近似于准静态热变形[21]。我们赞同桅杆在一个轨道周期的大部分时间内为准静态热变形的观点，但是对于文献[21]所述的初始阶段发生了明显的热振动的观点持异议。根据式(5)可知，若初始时刻Pε0(0)不等于0，则桅杆必将振动。由式(2)、式(3)可知，计算等效温度载荷需要已知温差，计算温差就需要一个参考温度。若参考温度不同，对于同一温度的结构，其热应变也不相同。对桅杆进行热诱发振动分析时，需要选取轨道上某一时刻为起始点，进行全周期的分析。若桅杆在分析起始时刻的在轨温度与有限元分析时设置的参考温度不同，则初始时刻桅杆上的等效温度载荷Pε0(0)就不等于0，桅杆在初始阶段即发生明显振动。但初始阶段的振动是由于初始条件引起的，而非真实的热振动。通过对桅杆进行两个连续周期的分析，如图4(a)所示，发现在第二个周期开始时并无明显振动，这也验证了第一个周期初始时刻的明显振动是由初始条件引起的。

通过对比分析可知，采用非耦合方法和全区间耦合单步内非耦合方法单独分析太阳翼桅杆的热诱发振动时，由于桅杆刚度比较大，固有频率比较高，温度载荷变化较缓慢，仅在分析初始阶段受初始条件的影响出现明显振动，且在阻尼作用下迅速衰减，在整个轨道周期内桅杆处于准静态热变形状态。

3柔性太阳翼热诱发振动分析

空间站柔性太阳翼结构复杂，在进行非耦合热诱发振动有限元分析时，对太阳翼模型进行了合理的简化。太阳翼的完整模型、材料、尺寸等略。

3.1柔性太阳翼有限元模型简介

太阳翼主要由箱体、桅杆和柔性阵面组成，如图5所示为太阳翼顶端的局部模型和单侧阵面的几何模型，太阳翼底端通过收藏筒和支撑杆连接在空间站的舱体上。太阳翼共有四个箱体，底部两个，顶端两个，箱体主要用于阵面展开前保护阵面，阵面展开后通过底部箱体上的张紧机构对阵面施加张紧力。桅杆逐节伸长，将阵面展开，对阵面起支撑作用。

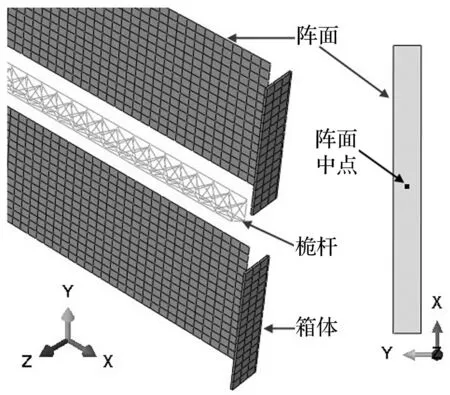
图5　太阳翼顶端局部有限元模型和单侧阵面几何模型 Fig.5 Finite element model of top part of the solar wing and a geometric model of a solar cell array

太阳翼顶端的箱体和同侧阵面间使用绳索连接，在有限元模型中使用多点约束(MPC)将阵面顶端边上节点与箱体上对应的节点连接。桅杆底端固支，桅杆顶端与箱体可以使用多点约束(MPC)连接，也可将箱体使用刚体约束关联到桅杆顶端的一个参考点上。其中，使用MPC约束时，箱体是弹性体；使用刚体约束时，箱体是刚体。由于箱体相对于阵面和桅杆的刚度比较大，并且经过对比发现，箱体作为弹性体或刚体对阵面的影响甚微，所以在本文中，箱体使用刚体约束。

3.2太阳翼温度载荷简介

太阳翼桅杆及阵面的在轨温度时刻变化，图6为入射角为0°工况下，阵面和桅杆上某个点在一个周期内的温度-时间曲线，起始时刻为出阴影区进入日照区。阵面温度在进出地球阴影区变化较快，温度高的时刻太阳翼位于日照区，温度低的时刻位于阴影区。太阳翼不同部件的材料、几何尺寸不同，在轨的温度变化也不相同。由太阳翼有限元模型各节点的温度-时间数据计算节点的等效温度载荷，并用于动力学分析。

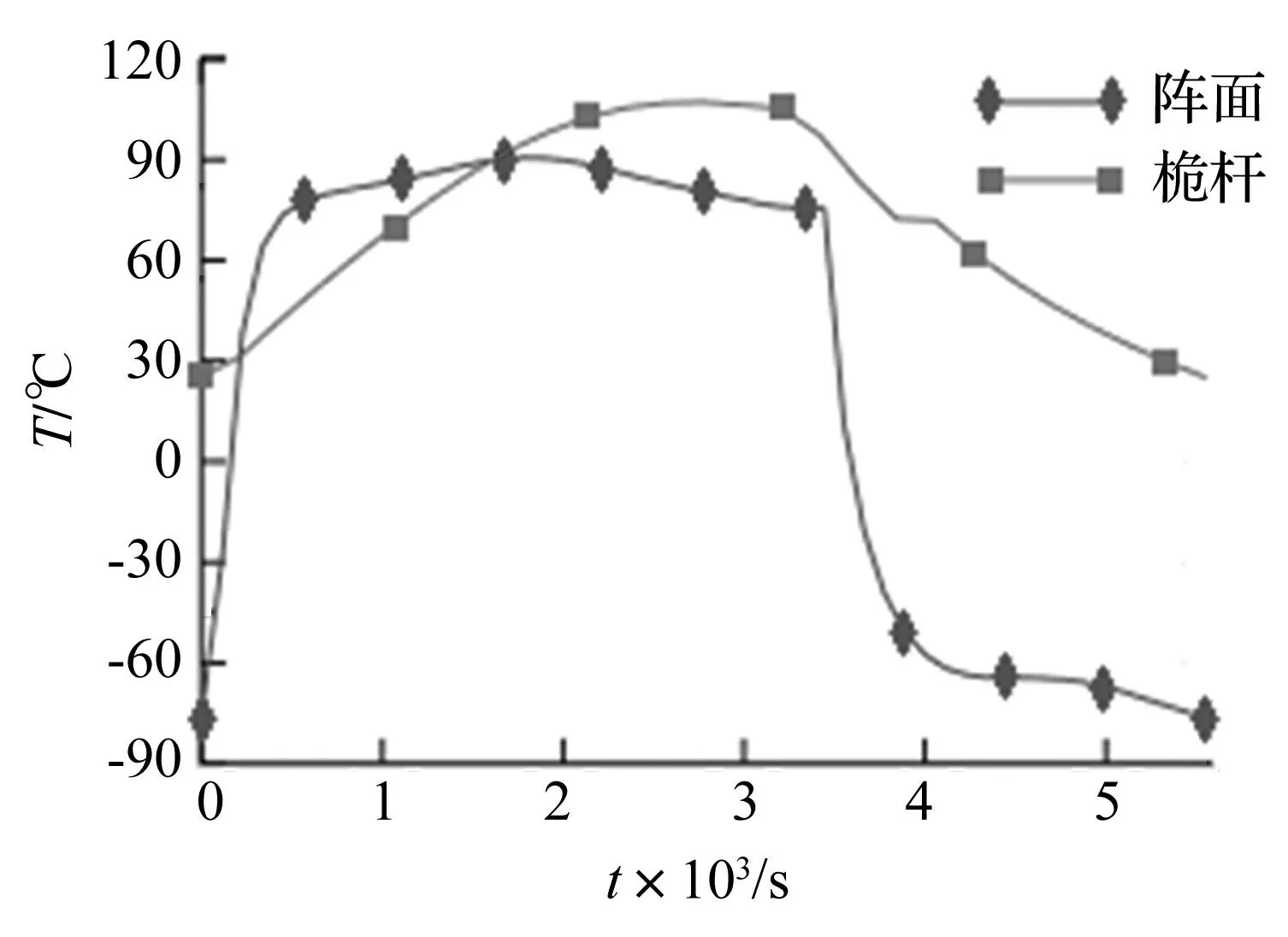
图6　阵面及桅杆上某点的温度变化 Fig.6 Temperature-time curves of solar cell plate and mast

3.3热诱发振动分析结果

对完整太阳翼模型进行连续多个周期的热诱发振动分析，得到了桅杆、阵面的位移响应，如图7所示，为桅杆顶端P1点(见图3)的3个周期的位移响应。图7与图4(a)对比可以发现，图7中每个周期始末的短时间内(200s左右)P1点沿Y轴、Z轴方向发生了明显振动，这段时间为太阳翼出阴影区进入日照区的过渡阶段，该时间段大致对应图6中首尾阶段。

图5中桅杆上侧的阵面中点沿X轴方向3个周期的位移响应如图8所示。图8中，负的位移对应图6中阵面的高温阶段。

因为阵面与底部箱体之间有张紧弹簧连接，而且阵面材料的热膨胀系数比桅杆材料的热膨胀系数大，所以当阵面温度升高膨胀时，在弹簧张紧力的作用下，阵面靠近底部箱体的一端会向底部箱体方向(X轴负方向)移动。阵面各节点的X轴向负位移随着X坐标的增大而减小。因此，图8中阵面中点在阵面高温时刻有X轴方向的负位移。图8中圆圈处放大后如图9所示。该时刻与图7中桅杆P1点在第2个周期末的明显振动时刻相同，但振幅都非常小。

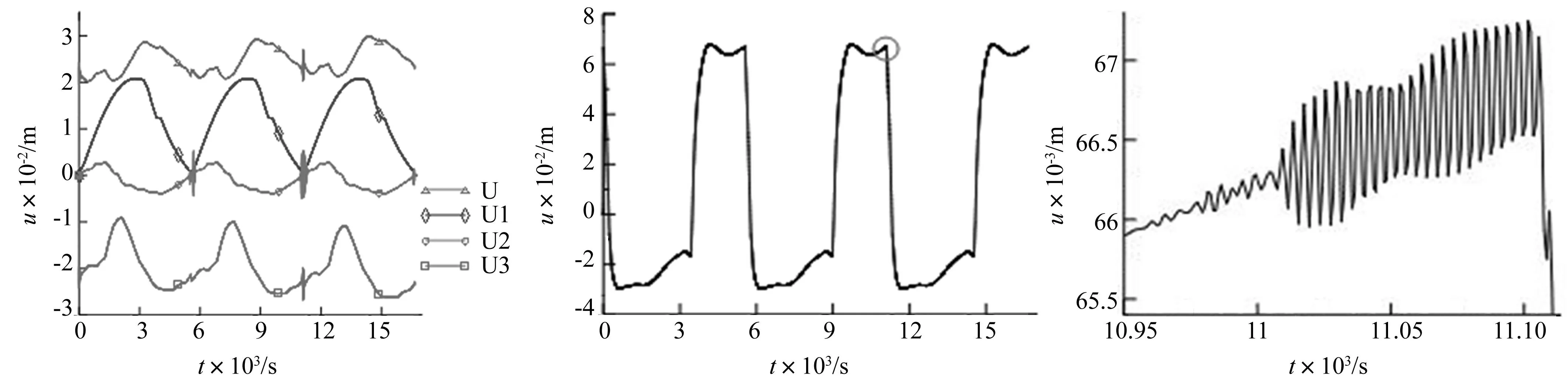
图7 桅杆顶端P1点位移响应Fig.7Displacementresponseofmast’spointP1图8 阵面中点沿X轴方向位移响应Fig.8Displacementresponseofsolarcellplate’scentralpointalongX-axis图9 阵面中点沿X轴方向位移响应局部放大Fig.9Partiallylargeversionofdisplacementresponseofsolarcellplate’scentralpointalongX-axis

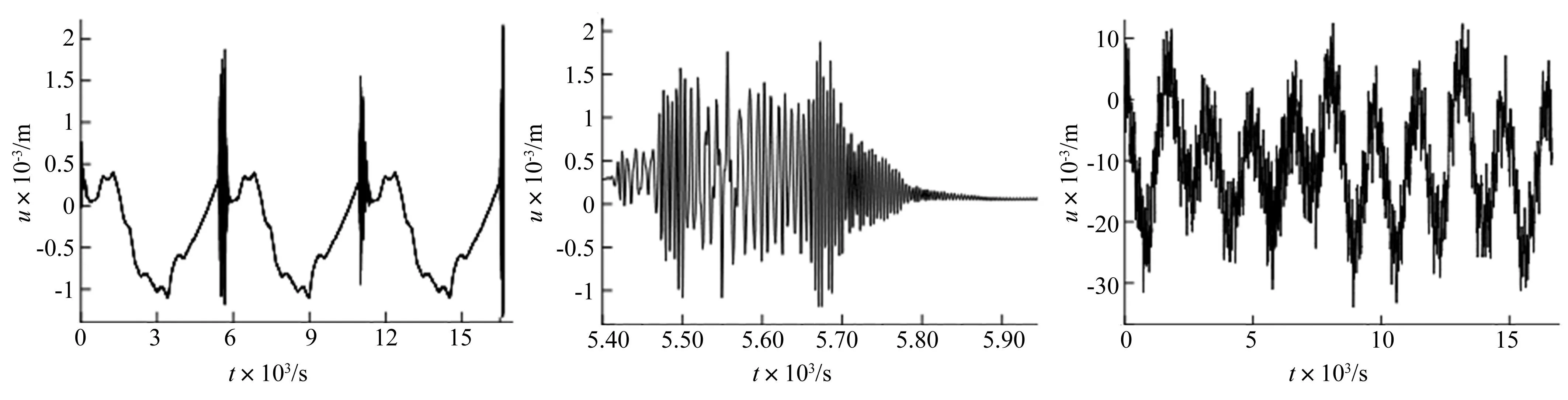
图10 阵面中点沿Y轴方向位移响应 Fig.10Displacementresponseofsolarcellplate’scentralpointalongY-axis 图11 阵面中点沿Y轴方向位移响应局部放大 Fig.11Partiallylargeversionofdisplacementresponseofsolarcellplate’scentralpointalongY-axis 图12 阵面中点沿Z轴方向位移响应Fig.12Displacementresponseofsolarcellplate’scentralpointalongZ-axis

阵面中点沿Y轴方向3个周期的位移响应如图10所示，该点与图8为同一点。由图10可以看到，在每个周期末有明显的振动，其中第1个周期末的明显振动放大后如图11所示。

阵面中点沿Z轴方向3个周期内的位移响应如图12所示，Z轴方向即阵面的法向。由图12可以看出，阵面在全周期沿法向具有明显的振动。第2个周期中间2 000 s的位移响应放大后如图13所示。

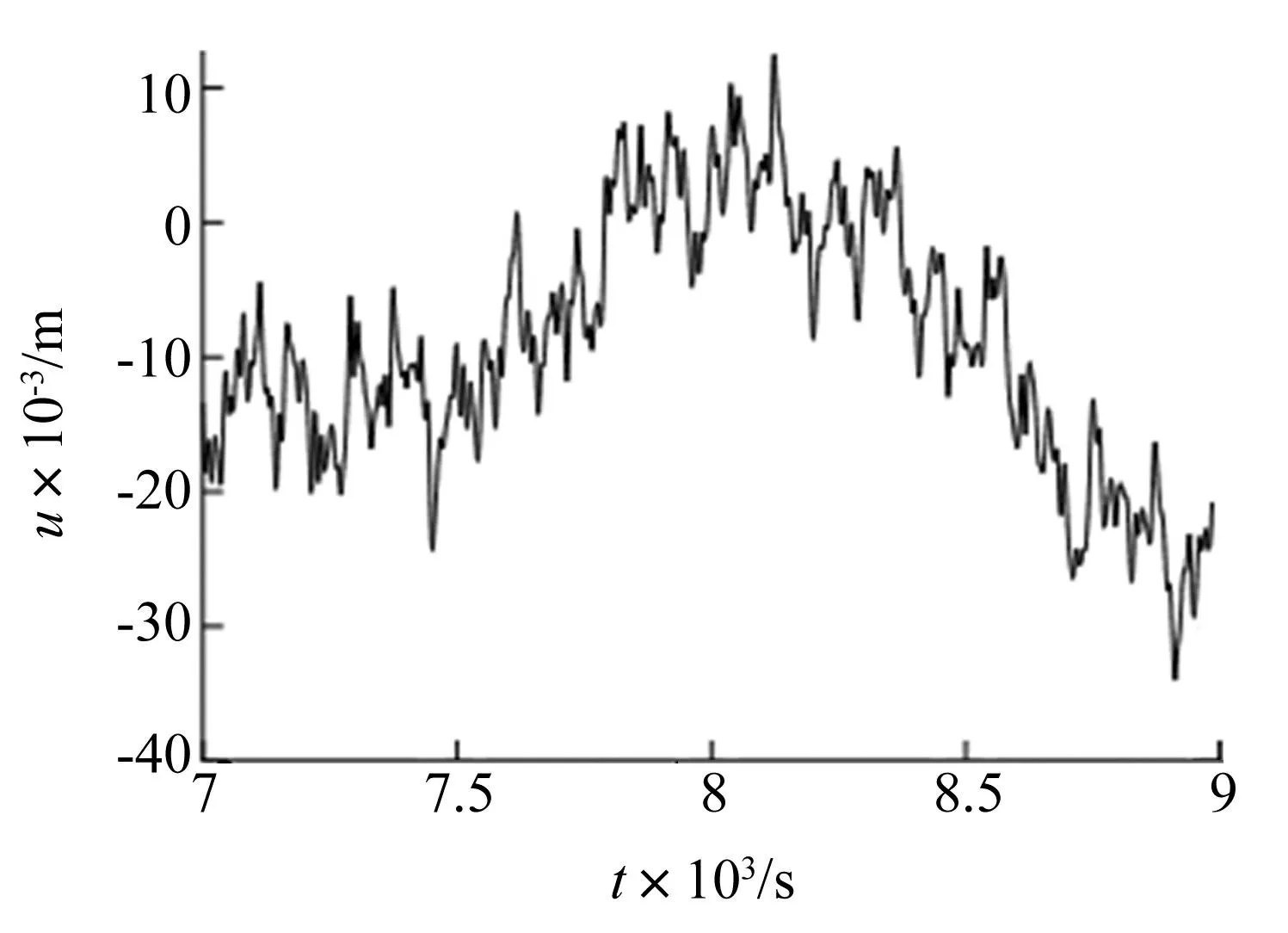
图13　阵面中点沿Z轴方向位移响应局部放大 Fig.13 Partially large version of displacement response of solar cell plate’s central point along Z-axis

3.3振动结果分析

由文献[21]的分析结果及图4可知，单独计算太阳翼桅杆的热振动时，由于初始条件的影响，桅杆在开始一段时间内有明显振动，但振动很快减弱，在全周期内，桅杆几乎为准静态热变形。由图7可知，当对柔性太阳翼整体进行分析时，在太阳翼出阴影区时的一段时间内，桅杆有明显的振动。造成图7与图4(a)中桅

杆振动差异的原因可能是桅杆与阵面的刚柔耦合。

由图8和图10可知，阵面沿纵向(X轴)和横向(Y轴)的位移在一个周期的大部分时间内近似准静态热变形产生的位移。在出阴影区进入日照区的一小段时间内有明显的振动，该振动时刻与桅杆的明显振动时刻相同，这应该是桅杆与阵面的刚柔耦合造成的影响。

由图12和图13可知，阵面沿法向(Z轴)在每个周期内都有明显的振动。在图12所示的3个连续周期内，忽略类似图13中的小振幅振动，可以发现有10个周期的大振幅振动，振幅为40 mm左右，周期约为1 600 s。在图13所示的2 000 s内有10多个周期的小振幅振动，振幅为10 mm左右，周期范围为100 s~200 s(按10~20个周期计算)。

虽然本文中太阳翼热振分析采用隐式动力学分析方法，而没有采用基于模态的振型叠加法，但是仍然可以将得到的振动结果与太阳翼的模态进行对比研究。图14为太阳翼第一、五、九阶模态的振型，对应的固有频率依次为6.09×10-4Hz、4.15×10-3Hz、9.54×10-3Hz，对应的周期依次为1 642 s、241 s、105 s。第一阶模态的周期与图12中大振幅的周期对比，可以发现两者非常接近；第五、九阶模态的周期与图13中小振幅的周期对比，可以发现它们也非常接近。太阳翼的低阶模态实际上为阵面的模态，根据图12和图13中阵面中点的法向位移响应与图14中3个模态的周期对比，可以推测在完整的轨道周期内，在热载荷的作用下可能激发出了图14所示的阵面3个模态中的某个或多个模态。

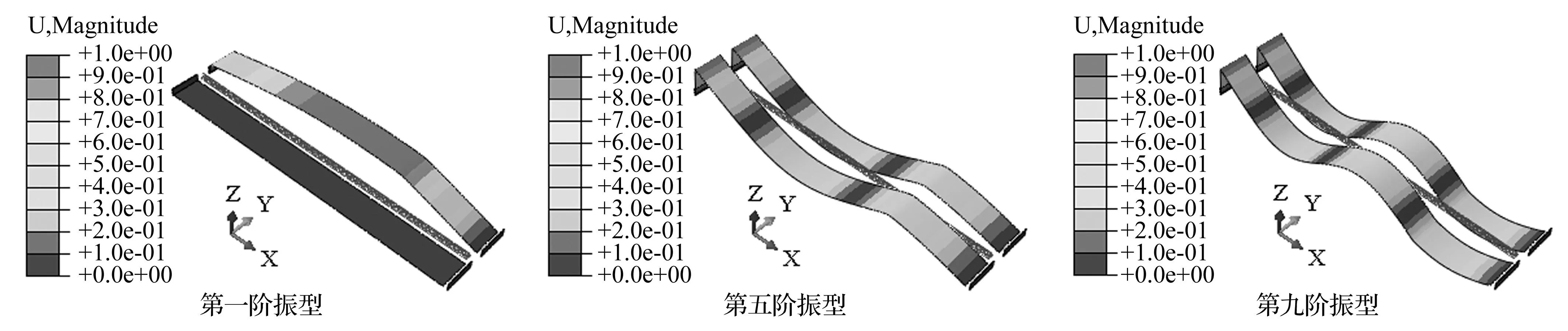
图14　第一、五、九阶模态的振型 Fig.14 The first, fifth and ninth mode shapes

由于太阳翼的轨道周期为5 500 s左右，约为太阳翼第一阶模态周期的3.35倍；太阳翼进出阴影区的时间为20 s左右，阵面温度发生大幅变化的时间为200 s~300 s，与太阳翼第五阶模态的周期接近。由此可以推测，太阳翼在轨道周期内的周期性的热载荷可能激发出第一阶模态，而进出阴影区时的突变热载荷可能激发出太阳翼的第五或九阶模态。

4结论

通过对空间站柔性太阳翼进行非耦合热诱发振动分析，得到了太阳翼在轨环境下受热载荷作用引起的振动情况。通过对太阳翼的热振动结果与太阳翼的低阶固有频率对比，发现了柔性太阳翼低阶固有频率与热振动频率非常接近。由于太阳翼的桅杆、阵面刚度差异较大，在热诱发振动分析中发现了太阳翼出阴影区进入日照区时的刚柔耦合问题。

本文使用的等效位移法可以精确计算等效温度载荷。对于温度突变或热冲击载荷作用下的结构的动态响应，由于作用时间极短，可以忽略热-结构的双向耦合，采用单向耦合或非耦合的方法也可以对结构的动态响应进行精确计算。

使用自编的Python有限元前后处理程序可以准确、高效地对等效温度载荷计算、动力学分析所需的数据进行读取、处理、加载等操作。

在工程应用中，采用热-结构耦合方法计算太阳翼等大型复杂结构的热诱发振动比较困难。在一定工程误差允许的前提下，采用热-结构非耦合方法可以对太阳翼的在轨热振动进行定性和定量地评估。本文所用的非耦合热诱发振动方法、求解等效温度载荷的等效位移法可以方便地应用于其他空间结构。

参考文献

[1]Boley B A. Thermally induced vibrations of beams[J]. Journal of the Aeronautical Science, 1956, 23(2): 179-181.

[2]Manolis G D, Beskos D E. Thermally induced vibrations of beam structures[J]. Computer Methods in Applied Mechanics and Engineering, 1980, 21(3): 337-355.

[3]Seibert A G, Rice J S. Coupled thermally induced vibrations of beams[J]. AIAA Journal, 1973, 11(7): 1033-1035.

[4]Kidawa-Kukla J. Application of the Green functions to the problem of the thermallyinduced vibration of a beam[J]. Journal of Sound and Vibration, 2003, 262(4): 865-876.

[5]Wattanasakulpong N, Gangadhara P B, Kelly D W. Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams[J]. International Journal of Mechanical Sciences, 2011, 53(9): 734-743.

[6]Shen Z, Tian Q, Liu X, et al. Thermally induced vibrations of flexible beams usingabsolute nodal coordinate formulation[J]. Aerospace Science and Technology, 2013, 29(1): 386-393.

[7]孙良新, 范绪箕. 热载荷作用下层合板瞬态响应分析[J]. 振动工程学报, 1989, 2(4): 12-22.

SUN Liang-xin, FAN Xu-ji. Transient response analysis of laminated composite plate subjected to suddenly applied heating[J]. Journal of Vibration Engineering,1989, 2(4): 12-22.

[8]夏巍, 杨智春. 热环境下复合材料壁板的振动特性分析[J]. 应用力学学报, 2005, 22(3): 359-363.

XIA Wei, YANG Zhi-chun. Vibration analysis to composite panels in thermal environment[J]. Chinese Journal of Applied Mechanics,2005, 22(3): 359-363.

[9]常晓权, 罗志伟, 郑钢铁. 基于混合单元建模的复合板热诱导结构振动研究[J]. 振动与冲击, 2006, 25(3): 18-24.

CHANG Xiao-quan, LUO Zhi-wei, ZHENG Gang-tie. Thermally induced vibration analysis of thin composite plate based on hybrid element model[J]. Journal of Vibration and Shock, 2006, 25(3): 18-24.

[10]Singha M K, Ramachandra L S, Bandyopadhyay J N. Vibration behavior of thermally stressed composite skew plate[J].Journal of Sound and Vibration,2006,296(4):1093-1102.

[11]Tran T Q N, Lee H P, Lim S P. Structural intensity analysis of thin laminated composite plates subjected to thermally induced vibration[J]. CompositeStructures, 2007, 78(1): 70-83.

[12]赵寿根, 王静涛, 黎康, 等. 考虑辐射散热叠层板热诱发振动的有限元分析[J]. 力学学报, 2010, 5: 978-982.

ZHAO Shou-gen, WANG Jiang-tao, LI Kang, et al. Finite element method analysis of thermally induced vibration of laminated plates considering radiation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 5: 978-982.

[13]Panda S K, Singh B N. Nonlinear finite element analysis of thermal post-buckling vibration of laminated composite shell panel embedded with SMA fibre[J]. Aerospace Science and Technology, 2013,29(11):47-57.

[14]徐向华, 任建勋, 梁新刚. 近地倾斜轨道航天器在轨热辐射分析[J]. 太阳能学报, 2004, 25(5): 717-721.

XU Xiang-hua, REN Jian-xun, LIANG Xin-gang. Thermal radiation analysis of spacecraft on inclined near-earth orbit[J]. Acta Energiae Solaris Sinica, 2004, 25(5): 717-721.

[15]李鹏, 程惠尔. 太阳电池阵极月轨道在轨热分析[J]. 空间科学学报, 2006, 26(4): 303-308.

LI Peng, CHENG Hui-er. Thermal analysis of the solar array in the lunar orbit[J]. Chinese J. Space Sci., 2006, 26(4): 303-308.

[16]陈忠贵, 张志, 廖瑛. 航天器太阳翼在轨光照角度建模及仿真分析[J]. 航天器工程, 2012, 21(1): 37-42.

CHEN Zhong-gui, ZHANG Zhi, LIAO Ying．Modeling and simulation analysis of solar illumination angle on spacecraft solar wing in-orbit[J]. Spacecraft Engineering, 2012, 21(1): 37-42.

[17]黄后学, 刘振宇, 陈娅琪, 等. 不同工况下空间太阳电池翼的在轨热分析[J]. 上海交通大学学报, 2012, 46(5): 790-795.

HUANG Hou-xue, LIU Zhen-yu, CHEN Ya-qi, et al. Thermal analysis of solar panels in orbit under different operating conditions[J]. Journal of Shanghai Jiaotong University,2012, 46(5): 790-795.

[18]姚海民, 薛明德, 丁勇. 大型空间结构热诱发振动的有限元分析[J]. 清华大学学报 (自然科学版), 2002, 42(11): 1524-1527.

YAO Hai-min, XUE Ming-de, DING Yong. Thermally induced vibration analysis of large space structures using the finite element method[J]. J Tsinghua Univ. (Sci. & Tech.), 2002, 42(11): 1524-1527.

[19]陶建忠, 雷勇军. 大型柔性太阳电池翼模态参数计算[J]. 湖南理工学院学报 (自然科学版), 2003, 6(4): 33-36.

TAO Jian-zhong, LEI Yong-jun. Modal characteristics analysis of large flexible solar panel[J]. Journal of Hunan Institute of Science and Technology (Natural Sciences),2003, 6(4): 33-36.

[20]黄彦文, 薛明德, 程乐锦, 等. 含开口薄壁杆的大型空间结构热诱发弯扭振动[J]. 清华大学学报 (自然科学版), 2005, 2: 262-266.

HUANG Yan-wen, XUE Ming-de, CHENG Le-jin, et al. Thermally induced vibrations of large space structures including thin-walled open beam sections[J].J Tsinghua Univ. (Sci. & Tech.), 2005, 2: 262-266.

[21]安翔, 冯刚. 某空间站太阳电池阵中央桁架热-结构耦合动力学分析[J]. 强度与环境, 2005, 32(3): 8-13.

AN Xiang, FENG Gang. Thermally induced vibration of the main mast of the space station’s solar arrays[J]. Structure & Environment Engineering, 2005, 32(3): 8-13.

[22]王焘, 冯刚, 张铎, 等. 柔性太阳电池阵的热-结构耦合分析[J]. 空间科学学报, 2002, 22(Ⅱ): 50-54.

WANG Tao, FENG Gang, ZHANG Duo, ed al. Analysis of heat-structure coupling on flexible solar cell series[J]. Chinese Journal of Space Science, 2002, 22(Ⅱ): 50-54.

[23]刘劲, 朱敏波, 曹罡. 星载可展开天线热振动数值分析[J]. 中国空间科学技术, 2011, 31(2): 53-57.

LIU Jin, ZHU Min-bo, CAO Gang. Numerical analysis of thermal induced vibration for deployable antenna[J].Chinese Space Science and Technology,2011, 31(2): 53-57.

[24]成新兴, 陈务军, 张淑杰. 空间充气可展薄膜天线热-结构耦合分析[J]. 四川兵工学报, 2011, 32(1): 127-131.

CHENG Xin-xing, CHEN Wu-jun, ZHANG Shu-jie. Coupled thermal-structural analysis of inflatable space membrane antenna[J]. Journal of Sichuan Ordnance, 2011, 32(1): 127-131.