Guldin定理在一类定积分计算中的应用

Guldin定理在一类定积分计算中的应用*

黄永

(云南昭通学院数学与统计学院,云南 昭通 657000)

摘要：围绕Guldin定理展开讨论，并利用初等几何和物理学的液体压力、有关功的定积分计算等问题分析思想方法，系统研究了Guldin定理，简化5类定积分的计算.

关键词：Guldin定理；定积分；计算问题；应用

文章编号：1007-2985(2015)01-0014-05

中图分类号：O186文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.01.005

收稿日期：*2014-07-23

作者简介：黄永(1966—)，女，云南昭通人，云南昭通学院数学与统计学院副教授，主要从事基础数学和数学教育研究.

Guldin(古尔金)定理是一个重要的定理，但在数学专业及各专业的《高等数学》教材中几乎没有提及，在物理专业的《高等数学》中主要是针对重心问题提出，也讲之甚少.然而，Guldin定理不仅在初等几何中能简化复杂的数学计算，而且其“重心思想”在物理学中液体压力、有关功的计算等方面也能起到化繁为简的效果，让微积分运算问题转化为初等数学的乘除运算，使得高等数学在工程技术和生产实际中有特殊的应用价值.

1预备知识及Guldin定理

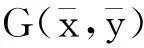
或

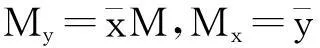
其中：Mx,My分别是n个质点对x,y轴的静力矩(质量为m的质点对于x,y轴的静力矩等于质量m与该点到x,y轴的距离的乘积，即为质量m与坐标y,x的乘积)；M是n个质点质量总和.若将质点组的全部质量集中在重心处，则它对某一轴的静力矩等于质点组对同一轴的静力矩.

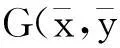
证明设平面薄板(曲边梯形)是由曲线y=f(x)及直线x=a,x=b,y=0所围成，其面密度为常数μ.

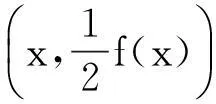
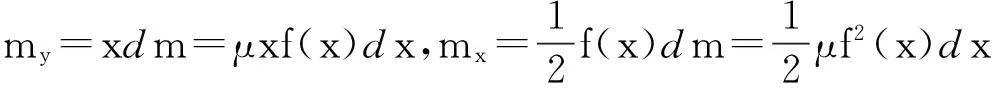
则平面薄板对y轴及x轴的静力矩为

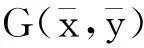
定理1(Guldin第1定理)平面曲线绕此平面上与其不相交的轴(可以是它的边界)旋转1周，生成的旋转体侧面积等于此曲线的重心绕同一轴旋转所产生的圆周长乘以该曲线的弧长.

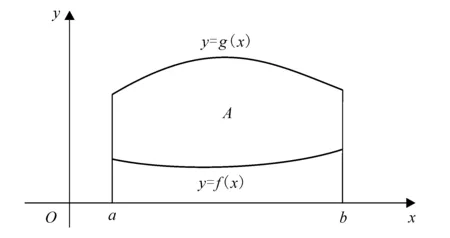
图1　平面图形A

定理2(Guldin第2定理)平面图形绕与其不相交的轴(可以是它的边界)旋转所得立体的体积，等于该平面图形面积与其重心绕轴旋转的周长的乘积.

证明不失一般性，设平面图形A是由曲线y=f(x)，y=g(x)及直线x=a，x=b所围成的(图1)，其面积为S,面密度为常数μ,则有平面图形质量为M=μS,再设f(x)≤g(x),f(x)≥0,g(x)≥0.那么，图形对于x，y轴的静力矩分别是

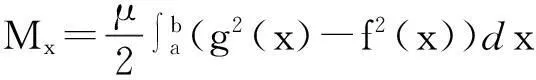
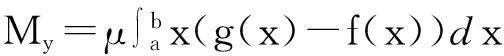
事实上,∀x∈[a,b],宽为dx,高为f(x)的小面积绕y轴所得旋转体体积微元为

dV=2πxf(x)dx(ΔV=π((x+dx)2-x2)f(x)).

于是,由y=f(x),x=a,x=b及x轴所围成的图形绕y轴所得的旋转体的体积为

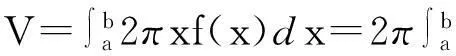
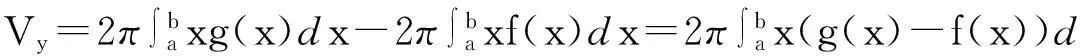
又因为图形对于y轴的静力矩

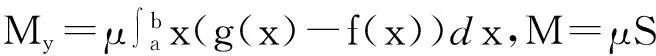
所以图形重心的横坐标

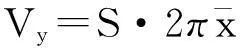
2Guldin定理的重心思想

Guldin第1定理给出了一条平面曲线Γ绕其所在平面上与其不相交的轴L(曲线Γ的端点可与L相交) 旋转1周而成的旋转曲面面积的计算方法.对于曲线重心到轴的距离以及曲线的长度容易计算时，利用古尔金第一定理可以很方便地求得旋转曲面的面积.

Guldin第2定理则给出一个平面图形Σ绕其所在平面上与其不相交的轴L(曲面Σ的边界可与L相交) 旋转1周而成的旋转体体积的计算方法.同样，对于平面的重心到轴的距离以及平面面积容易计算时，利用古尔金第2定理可以很方便地求得旋转体的体积.

要计算旋转体的侧面积和体积，有2个决定要素：一个是旋转前曲线Γ或平面图形Σ的大小，另一个是每个点旋转的路程(即弧长).由于每个点旋转半径不同，因此需要在曲线或平面图形上选择1个有代表性的点，该点的运动路程应是所有点运动路程的平均值，自然地，重心具有这一功能.古尔金定理利用物理学上的这一重要概念，集中了几何体的全部“质量” 这一特点，将一个几何图形看作是一个质点组，质点组的全部质量集中在重心处，则它对某一轴的静力矩(质点质量m与此点到轴的距离的乘积)等于质点组对同一轴的静力矩.此重心思想推广到曲线、平面的情形，则求重心的问题就转化为求静力矩的问题.

3Guldin定理的应用

3.1 几何体的有关计算

(1)求重心.

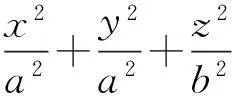
(2)求侧面积和体积.

例2计算圆周x2+(y-b)2=a2(b≥a)绕x轴旋转所得旋转体的侧面积和体积.

又因圆面积S1=πa2.由Guldin第2定理得旋转体体积为

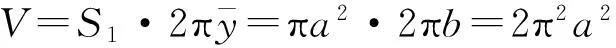
平面图形的面积S较易求得时，知道它的重心，则由Guldin定理很快就能计算出它绕坐标轴旋转所得立体的体积；反之，若知道平面图形绕坐标轴旋转所得的体积，同样地由Guldin定理也能迅速计算出它的重心.可见，Guldin定理是建立面积、体积和重心坐标之间关系的桥梁.

3.2 计算与液面垂直放置薄片一侧所受液体的压力

设液体比重为r，在相同深度处液体的静压强相同，其值等于液体的比重与深度的乘积,当Δx很小时，薄片上从深度x到x+Δx这一狭条所受的静压力为

Δp≈dp=rxf(x)dx，

则平面薄片所受的液体压力p为

其中A为平面薄片的面积，h为平面薄片重心到液面的距离.

例3一底为8 cm、高为6 cm的等腰三角形片，垂直沉没在水中，顶在上，底在下且与水面平行，而顶离水面3 cm，试求三角形片侧面所受的压力.

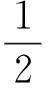
p=r·A·h=9.8×103×24×7=164.64 N.

3.3 有关功的计算

设液体比重为r，体积为V，重心到液面的距离为h,按3.2节中公式推导方法推得抽尽液体所做的功为

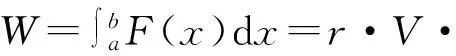
例4设一圆柱形蓄水池，深18 m，口径20 m，现用唧筒将16 m深的水全部抽出，求唧筒所作的功.

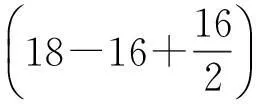
W=9.8×103×1 600π×10≈1.57×108πJ.

4应用Guldin定理需注意的问题

Guldin定理主要针对一些需定积分计算的几何体、液体压力、功等问题的简化计算.但是必须注意，只有当几何图形重心的位置和面积容易求出时，才能起到简化的作用.如例2中，当|b|

另外，Guldin定理还可应用于工程技术等更广泛的领域，比如解决风机设计过程中，对于形状不规则的回转体零部件质量的计算.其计算过程是，先求出回转体零件的体积，若已知该零件的密度，则可计算该零件的质量.这类问题，在此不予探讨.

参考文献：

四川大学数学系高等数学教研室.高等数学(物理类专业用).第1册.北京：高等教教育出版社，1987:350-353.

费定晖，周学圣.吉米多维奇数学分析习题集题解.第3册.济南：山东科学技术出版社，1981.

郜舒竹,徐春华.对旋转体体积的再认识.数学通报,2005(1):54-57.

方鸿珠,蔡承文.利用“重心”简化计算.南京工业职业技术学院学报，2005(9)：93-95.

陈志华.平面绕一定直线旋转所得旋转体体积计算的研究.高师理科学刊，2008(5):38-40.

Application of Guldin Theorem to Definite Integral Calculation

HUANG Yong

(College of Mathematics and Statistics,Zhaotong College,Zhaotong 657000,Yunnan China)

Abstract:Using elementary geometry,physics of liquid pressure,and the relevant analyzing methods for definite integral calculation,the author studies systematically Guldin theorem.The calculation of definite integrals of five classes is thus simplified.

Key words:Guldin theorem;definite integral;computing problems;application

(责任编辑向阳洁)