半连续dcpo的局部半基的若干理论

半连续dcpo的局部半基的若干理论*

祝祯祯,卢涛

(淮北师范大学数学科学学院,安徽 淮北 235000)

摘要：对连续格、半连续格、半连续dcpo等的相关定义与主要性质进行比较,得到它们的联系与区别,作出一些补充,并给出半连续dcpo的局部半基的概念,从而得到一些相关性质与结论.

关键词：连续格；半连续格；半连续dcpo；局部半基

文章编号：1007-2985(2015)01-0007-04

中图分类号：O153.1文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.01.003

收稿日期：*2014-04-15

作者简介：祝祯祯(1990—),女,安徽淮北人,淮北师范大学数学科学学院硕士研究生,主要从事格上拓扑学研究

通信作者：卢涛(1974—),男,山东诸城人,淮北师范大学数学科学学院副教授,博士,主要从事拓扑学和范畴论研究.

连续格理集序结构、代数结构、拓扑结构的研究于一体,取得了丰硕的成果,并对计算机应用产生了重要影响.为了推广连续格,Y.Ray首先提出格中半素理想的概念,研究了它的一些基本性质,文献利用半素理想,给出了一种新的关系,由此定义半连续格,并将连续格中的一些性质移植到了半连续格中,研究了半连续格的一些特征.而半连续dcpo的概念,其基本性质及特征亦能等价刻画,这些理论与思想能够用于更广泛的连续格理论当中.

1相关定义及主要结果

定义1设(L,≤)是偏序集,L的非空子集A称作定向集,若对于∀a,b∈A,∃c∈A使得a≤c且b≤c.L称作定向完备偏序集,若L的每个定向子集都有上确界.记↓x={y∈p:y≤x},x=∨D表示x是定向集D的上确界.

定义2L是偏序集,称I是L的理想,若I⊆L是L的定向下集.

定义3设L是一个偏序集,对∀a,b∈L,称aWaybelowb,若对任意的定向子集D⊆L,supD存在,对b≤supD,存在d∈D,使得a≤d.记为x≪y.

若定向子集D是理想,上述x≪y的定义即可类似改为：若对于任意的理想I⊆L,b≤supI,则a∈I.

定义4[1-2]设L是dcpo,若∀x∈L,x=∨Dx,则称L是连续dcpo或连续Domain.

定义5设L是dcpo,若∀x∈L,x≤∨Dx,则称L是弱连续dcpo或弱连续Domain.

定义6格L的理想P称为半素理想,若对∀x,y,z∈L,x∧y∈P,x∧z∈P时,有x∧(y∨z)∈P.

定义7设L是完备格,对∀a,b∈L,称a⟸Pb,若对于任意的半素理想P⊆L,b≤supP,则a∈P.

定义10偏序集L的理想Q称为素理想,若LQ为空集或滤子.

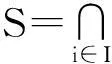
定义12设L是偏序集,∀a,b∈L,称a⟸Sb,若对于任意的半素集S⊆L,b≤supS,则a∈S.

定义13设L是dcpo,∀a,b∈L,称a⟸Sb,若对于任意的素理想Q⊆L,b≤supQ,则a∈Q.

对于定义5,若L是dcpo,则等价于定义6,故是合理推广.

定义14设L是dcpo,若∀x∈L,x≤∨Sx,则称L是半连续dcpo.

定义15设L是dcpo,若∀x∈L,x=∨Sx,则称L是强连续dcpo.

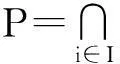
注4由引理1,这里若dcpo的L是完备格,则半素集S是理想,又由半素集定义,S是半素理想,则半连续dcpo与半连续格两者就等价了.

事实上,这里还可以列出相容定向集、相容连续Domain、弱waybelow关系、exact偏序集以及其他相关的概念,它们有极大的相似之处与紧密联系,当然,很多性质的研究方法也是相似的.

由以上分析能够得到以下结果：

(ⅰ)强连续格⟹连续格⟹连续Domain；

(ⅱ)连续格⟹半连续格；

(ⅲ)完备格+半连续dcpo=半连续格；

(ⅳ)弱连续dcpo⟹半连续dcpo；

(ⅴ)连续dcpo⟹强连续dcpo；

定理1(插入性质)L为连续格,∀x,y∈L,x≪y,则z∈L,x≪z≪y.

定理2(插入性质)L为半连续格,∀x,y∈L,则z∈L,x⟸Pz⟸Py.

定理3(插入性质)L为半连续dcpo,∀x,y∈L,则z∈L,x⟸Sz⟸Sy.

定义16L为偏序集,U⊆L,若满足如下2个条件,则称U为L上的Scott开集,Scott开集的全体构成L上的一个拓扑,称为Scott拓扑,记为σD(L)：

(ⅰ)U=↑U；

(ⅱ)对L的任意定向集D,当∨D存在且∨D⊆U时U∩D≠∅.

定义17L为偏序集,以{L↑x|x∈L}为子基生成的拓扑称为L的下拓扑,记为w(L),以w(L)∪σD(L)为子基生成的拓扑称为Lawson拓扑,记为λD(L).

定义18L为完备格,U⊆L,若满足如下2个条件,则称U为L上的Scott开集,Scott开集的全体构成L上的一个拓扑,称为Scott拓扑,记为σP(L)：

(ⅰ)U=↑U；

(ⅱ)对L的任意半素理想P,当∨P存在且∨P⊆U时U∩P≠∅.

定义19L为完备格,以{L↑x|x∈L}为子基生成的拓扑称为L的下拓扑,记为w(L),以w(L)∪σP(L)为子基生成的拓扑称为Lawson拓扑,记为λP(L).

定义20L为dcpo,U⊆L,若满足如下2个条件,则称U为L上的Scott开集,Scott开集的全体构成L上的一个拓扑,称为Scott拓扑,记为σQ(L)：

(ⅰ)U=↑U；

(ⅱ)对L的任意素理想Q,当∨Q存在且∨Q⊆U时U∩Q≠∅.

定义21L为完备格,以{L↑x|x∈L}为子基生成的拓扑称为L的下拓扑,记为w(L),以w(L)∪σQ(L)为子基生成的拓扑称为Lawson拓扑,记为λQ(L).

定理6设L为半连续dcpo,则∀x∈L,Qx∈σQ(L),L↓x∈σQ(L).

注5这3个定理均可通过上集、≪或⟸关系的概念、插入性质来证明.

定理7L为完备格,若对∀U∈σD(L),U⊆∪{Dx|x∈U},则L为连续格.

定理8L为完备格,若对∀U∈σP(L),U⊆∪{Px|x∈U},则L为半连续格.

定理9L为dcpo,若对∀U∈σQ(L),U⊆∪{Sx|x∈U},则L为半连续dcpo.

定义22设L为dcpo,x∈L,D⊆Dx,若满足如下2个条件,则称D为x的一个局部基：

(ⅰ)D是定向集；

(ⅱ)x=∨D.

定理10L为dcpo,a∈L,则：

(ⅱ)若a≪a,Da是a的局部基,则a∈Da；

(ⅲ)若a≪a,{a}是a的最小局部基；

(ⅳ)若b≤a,且Da,Db分别是a,b的局部基,则Db⊆↓Da.

定理11设L为连续Domain,a∈L,D⊆Da,则D为a的一个局部基当且仅当对∀c∈a,∃d∈D使得c≪d.

事实上,连续格上的局部基也是一样的.

(ⅰ)D是定向集；

(ⅱ)x=∨D.

显然,由此定义亦能得到连续格的相关性质定理,而半连续格的相关定义和结论与连续格是紧密联系的,这里可参考文献.从而可以定义半连续dcpo的半局部基,将相关结论补充完整.

定义24设L为dcpo,x∈L,S⊆sx,若满足如下2个条件,则称S为x的一个局部半基：

(ⅰ)↓S是素理想；

(ⅱ) x≤∨S.

定理12设L为dcpo,L是半连续dcpo当且仅当∀x∈L,x都有一个局部半基.

定理13设L为dcpo,x∈L：

(ⅱ)若x⟸Sx,{x}是x的最小局部半基；

(ⅲ)若x⟸Sx,Sx是x的局部半基,则x∈↓Sx；

(ⅳ)若x⟸Sx,则Sx是x的局部半基；

(ⅴ)若b≤a,且Sa,Sb分别是a,b的局部半基,则Sb⊆↓Sa.

证明(ⅲ)设Sx是x的一个局部半基,则Sx⊆Sx且x≤∨Sx=∨↓Sx≤∨Sx,因为x⟸Sx,即对任意的素理想Q,x≤∨Q,x∈Q,所以x∈↓Sx.

(ⅴ)由Sa是a的局部半基知,↓Sa是素理想且a≤∨Sa,再由Sb是b的局部半基,对∀x∈Sb,x⟸Sb,因为b≤a,所以x⟸Sa,从而x∈↓Sa,因此Sb⊆↓Sa.

定理14设L为半连续dcpo,a∈L,S⊆Sa,则S为a的一个局部半基当且仅当对∀c∈Sa,∃d∈S使得c⟸Sd.

定理15L为完备格,L是半连续dcpo当且仅当∀x∈L,x都有局部半基.

2结语

对几类经典的连续格的相关定义与主要性质进行比较,作出一些补充,扩充了连续格理论,对于连续偏序集、相容连续偏序集、弱Domain、exact Domain等的一些结论也类似可得.而这些理论与思想又可以推广到更广泛、更一般的连续格领域,从而可能得到创造性的结论.

参考文献：

[1]GIERZ G.Continuous Lattices and Domains.New York：Cambridge University Press,2003.

[2]赵斌,刘妮.连续Domain的特征与浓度.陕西师范大学学报：自然科学版,2002,30(2)：1-3.

[3]伍秀华,李庆国.半连续格的刻画和映射.数学研究与评论,2007,27(3)：655-658.

[4]刘玉连,李高林,徐罗山.半连续dcpo.扬州大学学报：自然科学版,2012,15(2)：1-5.

[5]李娇,徐晓泉.相容连续Domain的序同态扩张.江西师范大学学报：自然科学版,2011,35(4)：373-374.

[6]ABRAMSKY S,JUNG A.Domain Theory.New York：Oxford University Press,1994.

[7]陈昱.半连续格及相容连续偏序集研究.扬州：扬州大学,2009：11-21.

[8]徐罗山.相容连续偏序集及其定向完备化.扬州大学学报：自然科学版,2003,3(1)：1-6.

Theories of Local Semi-Bases on Semi-Continuous dcpo

ZHU Zhenzhen,LU Tao

(School of Mathematical Sciences,Huaibei Normal University,Huaibei 235000,Anhui China)

Abstract:The relevant definitions and main properties are compared among the continuous lattice,semi continuous lattice and semi continuous dcpo,and thus their relations and differences are obtained.Some supplements are made and the concept of local semi-base about semi-continuous dcpo is introduced.Furthermore,some relevant properties and conclusions are obtained.

Key words:continuous lattice;semi-continuous lattice;semi-continuous dcpo;local semi-base

(责任编辑向阳洁)