环形管道的阻力计算及模拟分析

环形管道的阻力计算及模拟分析

主要研究管道内气液两相流的基础理论和实验。

徐凯，赫永鹏，吴东垠

(西安交通大学能源与动力工程学院，西安 710049)

摘要：环形管道具有结构紧凑、传热面积大、流动性好、传热系数高等显著优点，已经得到了广泛的应用。首先，对环形管道的阻力特性进行分析计算，分析了雷诺数、环形管道间隙、当量直径对阻力系数的影响，发现对于某给定的环形管道，其阻力系数与其对应的雷诺数的乘积为常数，其值约为96。其次，用Fluent软件对环形管道内部流场进行数值模拟，发现环形间隙内流体沿着管道流动方向压力逐渐降低，并且伴随有流速在小范围内升高。

关键词：环形通道；阻力特性；数值模拟

0引言

随着我国经济的飞速发展，能源消耗急剧上升。我国作为第一大能源消耗国，虽然能源资源丰富，但人均能源资源占有量低，能源资源地区分布不均衡，能源结构以煤炭为主。同时，巨大的能源消耗带来了严重的环境污染，对未来经济的可持续发展带来严峻的考验。基于我国能源结构问题和能源资源紧缺现状，对环形管道的阻力特性进行分析研究具有深远的现实意义。一方面，环形通道具有换热面积大、结构紧凑等诸多优点,在新型核动力装置、电子元器件、航空航天和能源的梯级利用等工程领域得到了愈来愈广泛的实际应用[1-2]。另一方面，对于工农业及日常生活，传统的供热方式多为各自独立的热流体供热管道和冷流体回流管道，高温供热管道仅靠保温层裸露在室外环境，由于较大的温差而造成巨大的热量损失。人们针对热网进行了较多的研究[3]，同时，提出了一种新型的高效节能紧凑环形管道，通过内管包有保温层套上一中间管，中间管与外管再通过支撑架连接形成环形通道，从而实现同时完成热流体供热和冷流体回流的功能系统，具有明显的节能效果[4]。国内外已有的研究成果表明，环形流道流体阻力特性不同于圆管的阻力特性，不同间隙尺寸的环形流道流体阻力特性不同。目前的研究结果存在较大的差异，不仅定量结果不同，而且在环形流道间隙对阻力系数影响的趋势上，甚至得出相反的结论[5]。本文研究环形通道内流体流速、压力、雷诺数及环形通道的几何参数等对环形通道阻力特性的影响机理，对于环形通道的应用和发展具有一定意义上的积极作用。

1环形管道内流动阻力计算理论分析

目前国内外学者关于环形管的研究主要集中于环形管内或窄缝环形管道内的流动和传热状况，而对于流体在环形管道外做纵向流动传热的情况研究较少，特别是对工程中膜式螺旋管换热器壳程为同轴环形通道还没有相关介绍[6]。鉴于环形通道在供热方向的应用背景，对于大型、长距离输送、主辅热源联合供热的热网，它可以显著地节约铺设管网的成本和有效地减少热损耗，因此，环形管道的管内流动状态参数对供热管网如何降低热损耗，提高热效率有重要的指导意义。由于已有研究的不充分性，本文将就环形管道内流体流速、雷诺数及几何参数对同轴环形通道阻力特性的影响进行研究分析。

对于普通的非圆形流道，因为缺乏大量可信的实验数据，所以目前的计算方法尚未统一。不过，对于普通的同心环形流道，其层流流动动量微分方程及其边界条件为：

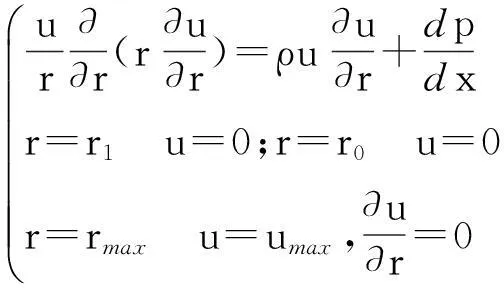
(1)

同时，注意到在层流充分发展区有：

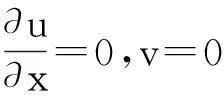
(2)

因此，可以通过式(1)、式(2)得到环形管道的阻力系数λ的计算公式(3)：

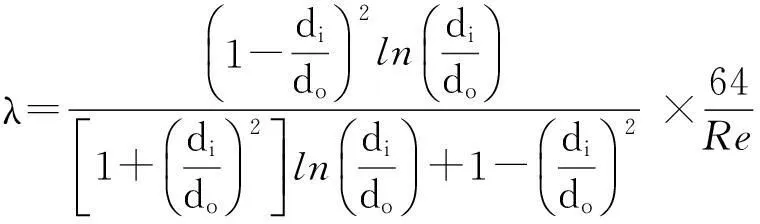
(3)

式中：λ为环形管道的阻力系数；do为环形管道的外管内径(m)；di为环形管道的内管外径(m)；Re为环形管道内流体的雷诺数。

环形管道内流体的雷诺数的计算如式(4)：

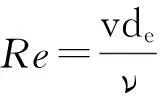
(4)

式中：v为环形管道内流体的流速(m/s)；de为环形管道的当量直径(m)；ν为环形管道内流体动力黏度(m2/s)。

环形管道的当量直径通过式(5)求解：

(5)

式中：A为非圆形管道实际过流面积(m2)；χ为非圆形管道实际过流湿周周长(m)。

通过以上参数的计算，再代入式(3)，就可以计算出环形管道内的阻力系数。

2环形管道内阻力计算

2.1不同间隙管道阻力系数随雷诺数的变化

现以与文献[4]相关的新型输热管道中的环形管道为例，分析在雷诺数Re为300～8 000的范围内，不同环形通道间隙的管道阻力系数的变化。环形管道外管内径do为15.1 mm，环形管道的有效长度为200 mm，实验介质为饱和水。分别取环形管道间隙h为0.3 mm、0.8 mm、2 mm、2.3 mm、2.5 mm、2.7 mm，在同样的雷诺数变化范围内，环形管道内流体的阻力系数的计算结果见表1。

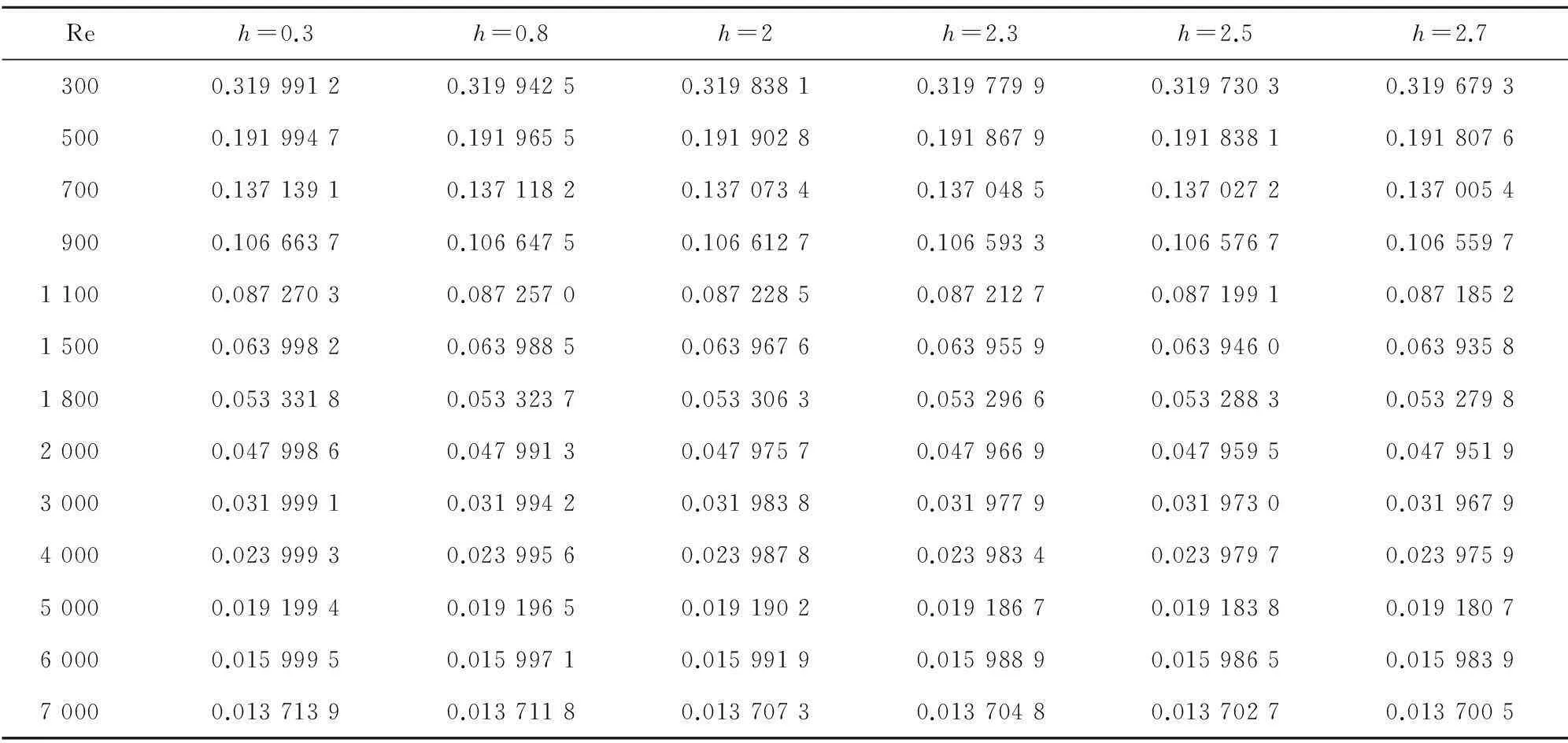
表1　不同环形间隙下阻力系数随雷诺数变化结果

根据表2的数据我们绘制出对应的坐标图1，以观察不同环形间隙下阻力系数随雷诺数的变化情况。

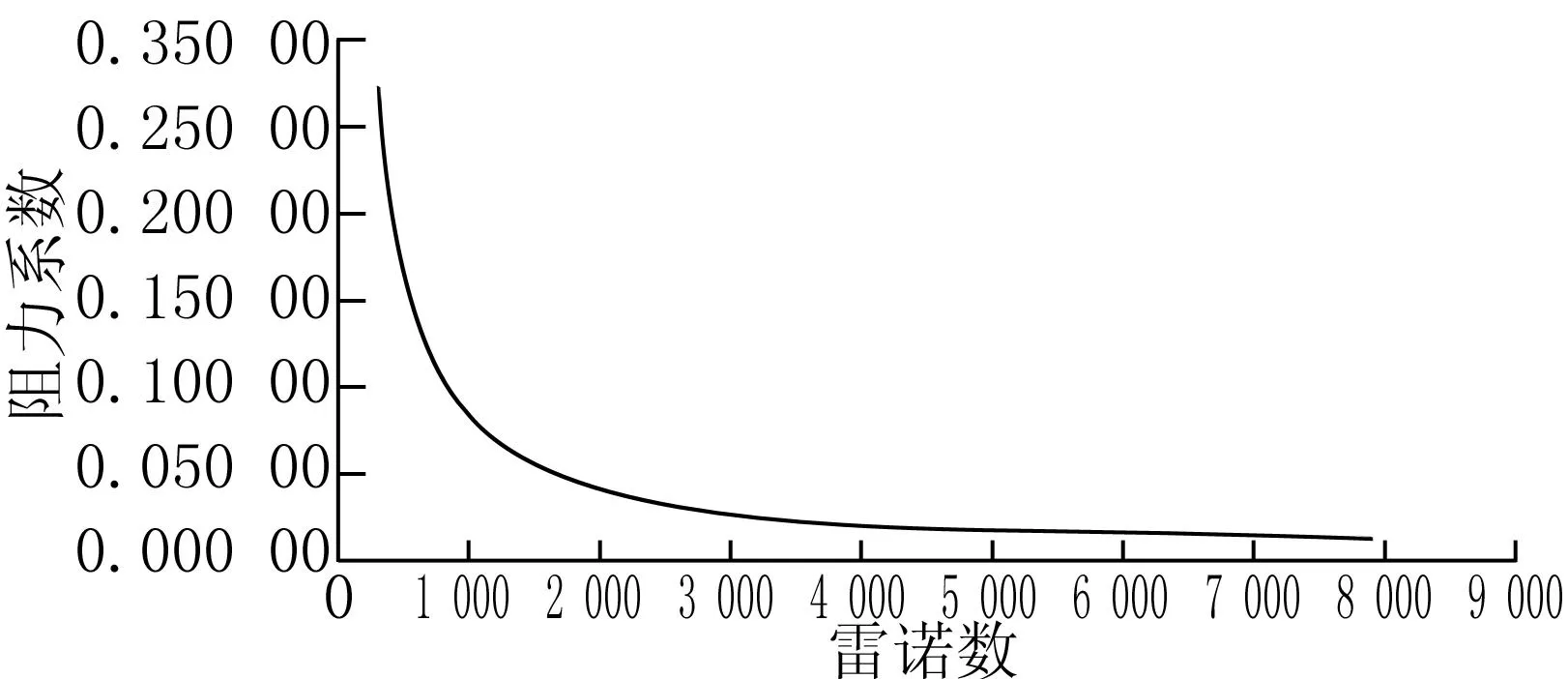
图1　不同环形间隙下阻力系数随雷诺数变化

由图1我们可以得到以下结论：在任何间隙下，环形管道内的阻力系数总是随着雷诺数的增加而减小，并且当Re>4 000以后，阻力系数随雷诺数的增加而变得平缓，最终趋于水平，即管内阻力系数几乎不随雷诺数的增加而增加。环形管道内流体的流动，其层流与湍流间的转捩雷诺数随着间隙的增大而增大。其原因可以分析如下：由于随着管道内流体雷诺数的增加，流体湍动度增加，内部流场扰动增强，使得紧贴壁面处的黏性底层遭到破坏，随着边界层厚度的减薄，流体流动阻力系数自然随之降低，即环形管道内阻力系数随雷诺数的增加而减小；当雷诺数较大时，出现阻力系数随雷诺数的增加而趋于水平变化，原因可能由于管道内流体流动随着雷诺数的增加出现了自模化现象，同时边界层已经减得很薄，其对流动阻力影响作用降低。

为分析环形管道间隙的变化对阻力系数的影响，绘制了在Re为300和5000情况下阻力系数随间隙h的变化情况，如图2所示。在Re一定的情况下，环形管内阻力系数大小随着间隙的增大而减小，此处仅仅列出来Re=300和Re=5 000的2种情况，在其余Re工况下环形管阻力系数随环形间隙的变化规律是一致的。原因可能是随着环形间隙的增大，黏性底层对阻力系数的影响作用减小，当间隙越小时，流体边界层在纵向方向上占据较大的比例，使得流体流动受到较涡流更大的影响作用。

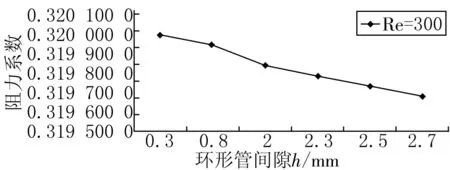
(a)Re=300

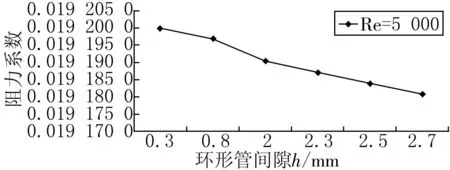
(b)Re=5 000图2　Re一定时阻力系数随间隙的变化情况

进一步对表1的数据进行处理，我们不难发现这样的规律：那就是雷诺数与阻力系数的乘积近似一个常数，以间隙h=0.8为例进行说明，我们将雷诺数与其对应阻力系数相乘，将计算结果记录在表2中。

从表2中可以看出不同雷诺数下的雷诺数与其对应的阻力系数的乘积相同，但是经过一番验算得知，每一组的乘积结果并不都是95.982 775，由于计算机计算结果将小数点最后几位是随机取舍的，所以每组雷诺数与阻力系数的乘积是相近的，而不一定相等。但是，从表2中我们仍然可以得出这样的结论：环形管道其流体流动的特征数雷诺数与其对应的阻力系数值相乘结果约等于96。从这一发现我们就不难解释为什么随着雷诺数的增加，对应的阻力系数值逐渐降低。同时，我们也可以利用这一发现来估计同一环形管道在不同雷诺数下的阻力系数值，从而为环形管道的设计运行提供有力的理论支持。

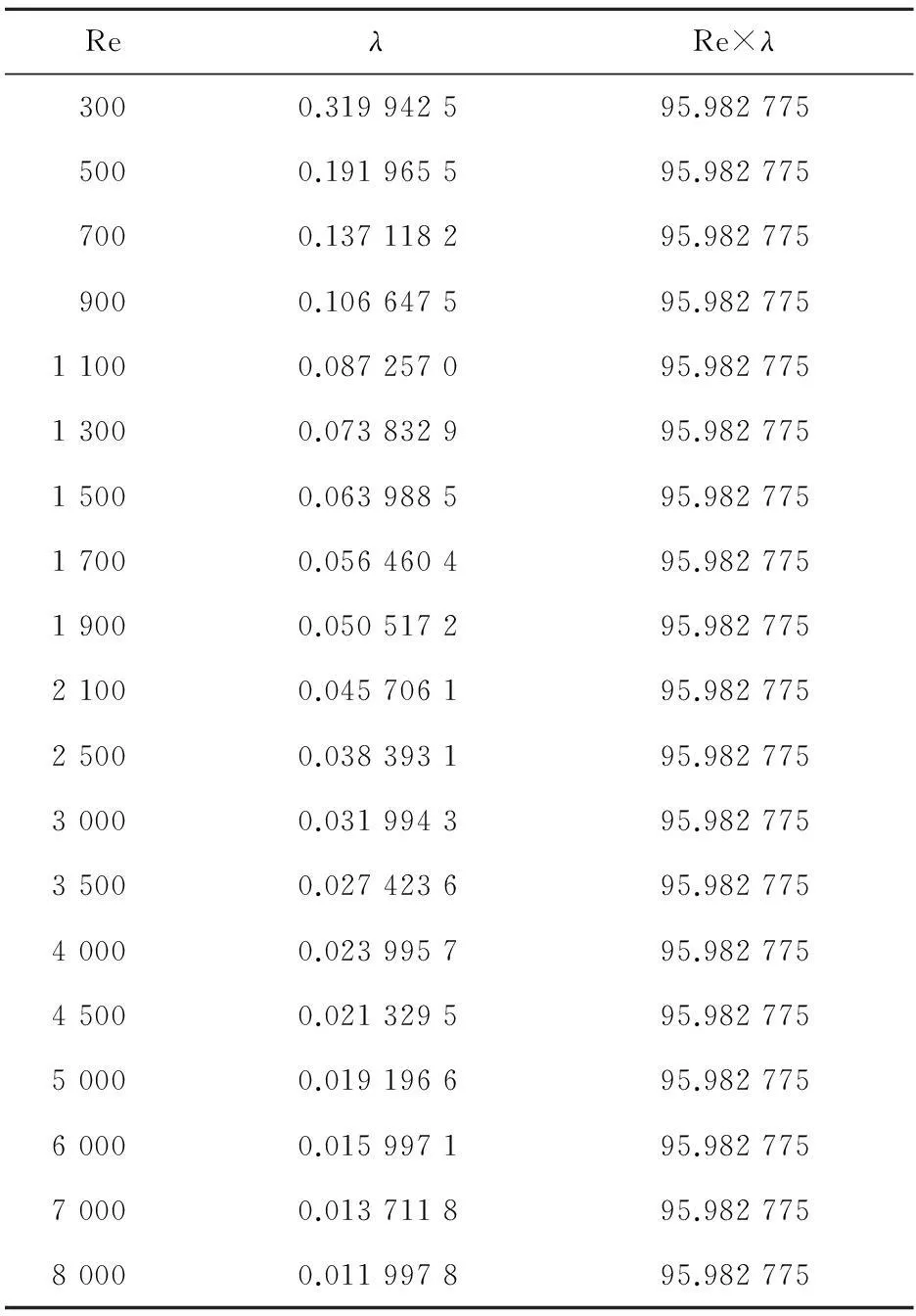
表2　阻力系数与雷诺数乘积结果

2.2环形管道不同当量直径情况下阻力系数的变化情况

对于环形管道，将实际过流面积和实际过流湿周周长用外管内径do和内管外径di表示，代入公式(5)，则可以得到环形管道的当量直径表达式，如公式(6)和式(7)。

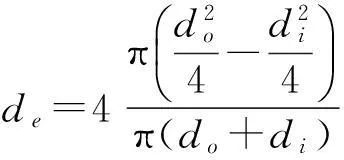
(6)

即：

de=do-di=2h。

(7)

即环形管道的当量直径就是2倍的环形间隙。所以，对于环形管道的阻力系数随环形间隙的变化规律亦可以理解为环形管道的阻力系数随当量直径的变化规律。

3基于Fluent软件对环形管道内流场的分析

基于Fluent平台对环形管道内的流场进行模拟，通过分析环管内流场图，有助于进一步分析环形管内阻力产生的区域及原因。可通过流场参数设置的改变观察流场图形的变化，分析环形管道阻力的影响因素。

首先在Gambit软件中建立环管模型。所建环形管的模型如图3所示，其中结构设置为管长L为10 m，内管外径di为0.4 m，外管内径do为0.8 m。

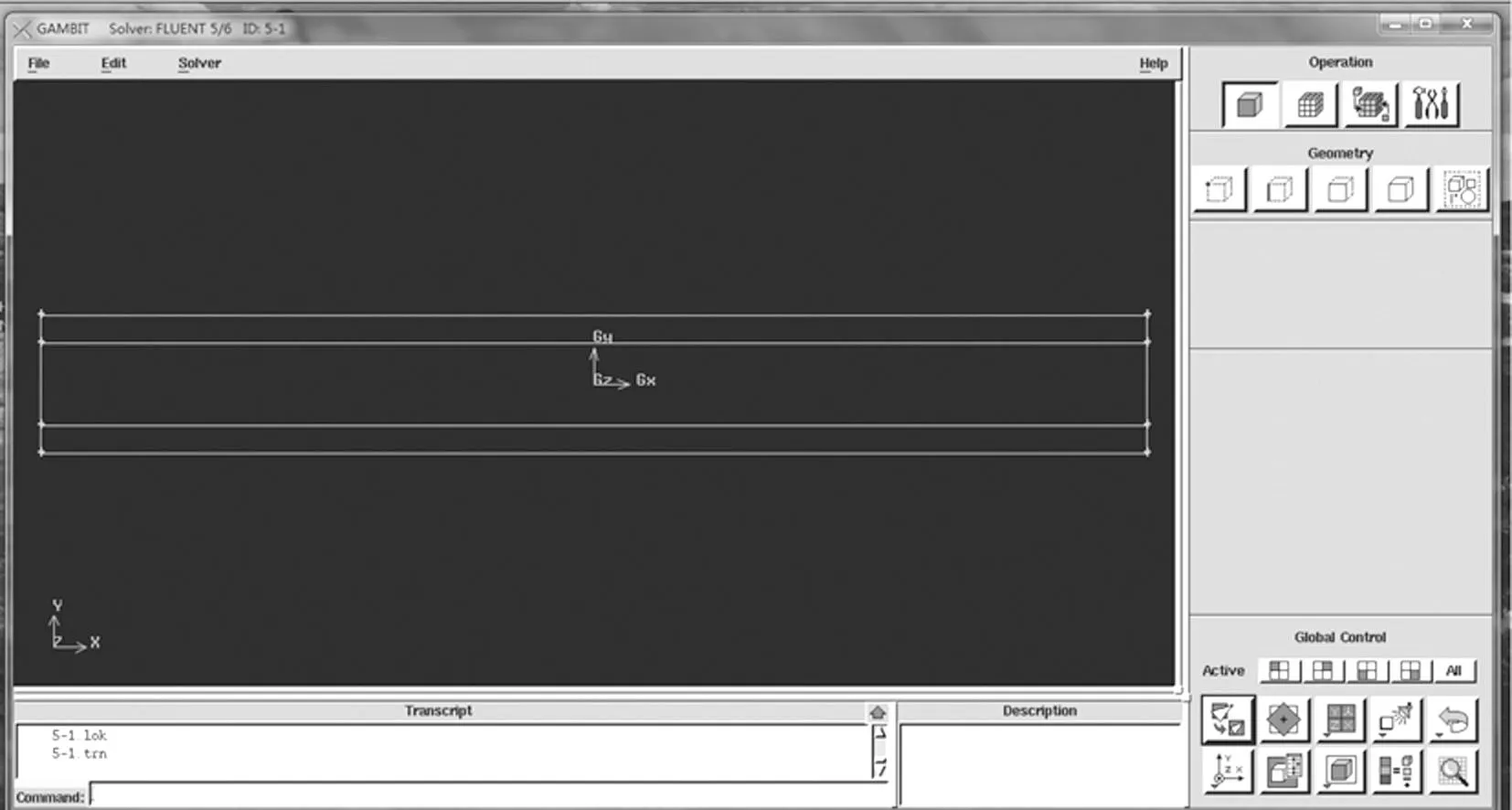
图3　环形管道模型

对计算区域进行网格划分，如图4所示。

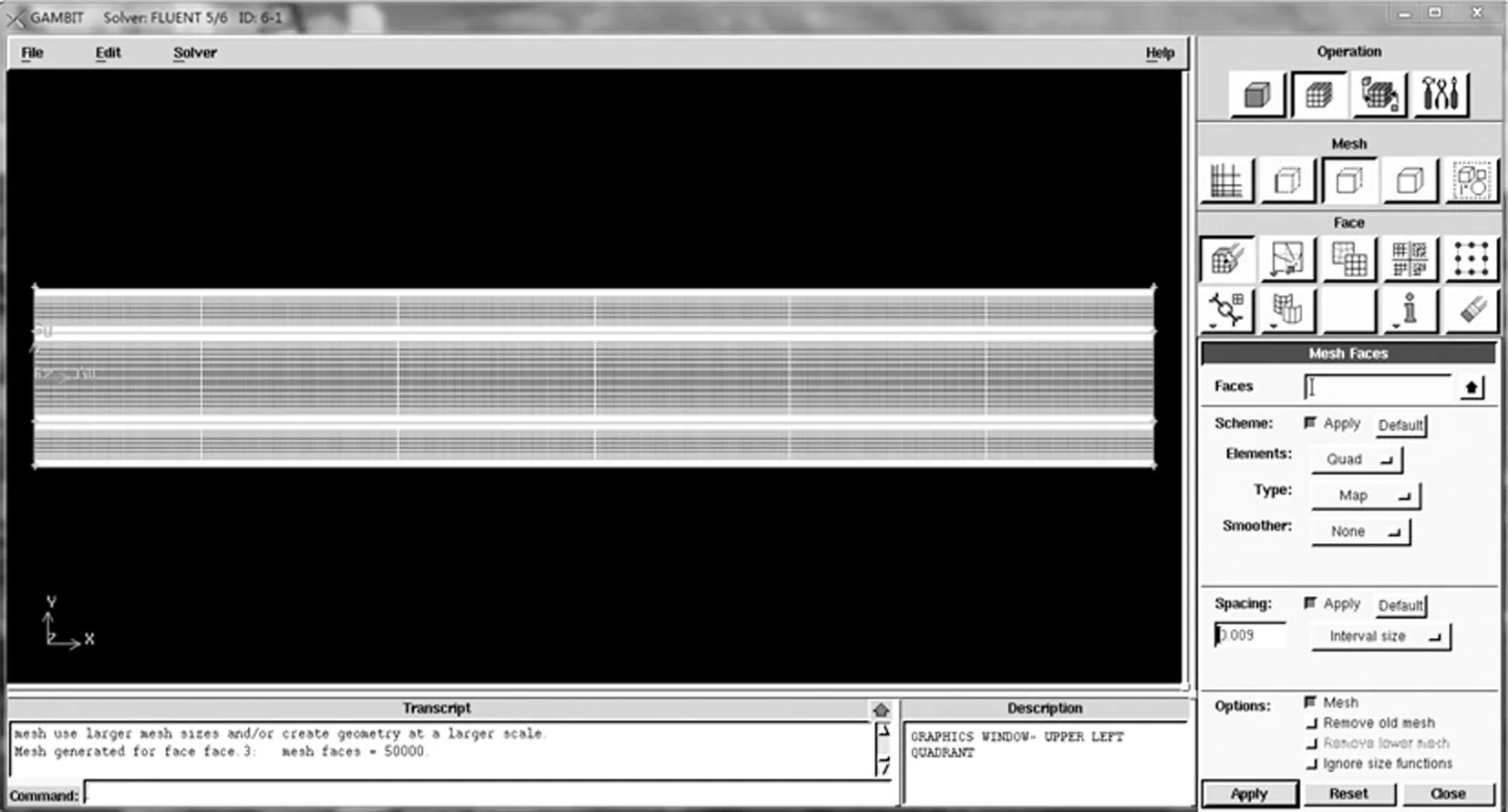
图4　环形管道模型网格划分

本次网格划分数为50 000，对于数值模拟中的网格划分，网格划分越细得到的图形越精确，相对来说结果也准确。但是划分数目越大，计算机运行的计算工作量也随之增大，耗费的时间也就越长。所以，选取合适的网格划分数对于进行Fluent软件的数值模拟是十分有必要的。

随后，我们需要对模型进行边界设置。本次模拟环形管道流动采用逆流式布置。最左边管道的上下2个环形间隙通道设为入口inlet-1、内管设为out-2、最右边管道的上下环形间隙设置为out-1、内管设置为inlet-2；其中inlet-1为速度进口，进口速度inlet-1-velocity=1 m/s，inlet-2为压力进口，inlet-2-pressure=1 000 Pa，out-2-pressure=100 Pa，out-1-pressure=800 Pa。将Gambit中所建模型以.msh文件输出，然后将.msh文件导入到Fluent中进行求解计算。

由于本文着重关注环形管的阻力状况，而并不涉及热量传递分析，所以，在Fluent中并未启动能量方程，不需要对流体温度进行设置。经过Fluent软件迭代计算，并确定结果达到收敛要求，计算终止。

图5　环形管道内压力场分布云图

从图5中我们可以看到，在内管流体从右向左流动时，压力随着流体流动方向明显降低；在环形间隙内流体从左向右逆向流动时，压力也是随着流体流动的方向逐渐降低。根据流体力学流体流动的阻力特性分析得知，任何管道内的流体流动过程都伴随着能量的耗散，因此就不难解释图中压力降低的原因：由于流体黏性阻力作用，导致流体压力降低。因此，通过公式精确计算阻力系数在管道和流场的设计中具有非常重要的意义。

研究环形管内的阻力特性，除了要关注流道内的压力变化，流道内的速度分布规律也是十分重要的一部分。因此，应在Fluent中展示出环形管道内速度场的分布，如图6所示。

图6　环形管道内速度场分布云图

从图6中我们看到，在中间流道内中间的地方速度最大，随后向两边逐渐降低，这些现象运用边界层理论可以解释，为了便于观察我们将图6进行局部放大，得到图7。

图7　环形管内速度云图局部放大图

从图7中我们还可以发现，在流动方向上流体流速在小范围内升高，分析其原因可能是由于流体在流动方向上压力降低导致流体密度降低，使得单位时间内在固定壁面流道内的体积流量增大，所以，反映在速度变化图上就是流速有略微的增加。

普朗特的边界层理论认为诸如水、空气等普遍具有黏性的流体流过物体表面时，由于黏性作用的影响仅限于靠近壁面的薄层中，而在这一薄层之外，黏性的影响可以忽略，也就可以当成理想流体来对待。流速自壁面到速度不再改变时的距离称为边界层的名义厚度[7]。

从运用数值模拟软件对环形管道内流场的模拟结果得出：环形间隙内流体沿着管道方向压力逐渐降低，并且伴随有流速在小范围内升高。管道内流体流动过程，由于黏性阻力作用，导致流体的阻力系数大，在流动中产生能量的消散，导致流体压力降低。而流体流速有升高的可能是由于流体在流动方向上压力降低导致流体密度降低，使得单位时间内在固定壁面流道内体积流量增大，所以反映在速度变化图上的流速有略微的增加。

4结语

本文分析了环形管道流动阻力系数的影响因素，并对环形管道进行建模，利用Fluent软件平台分析环形管道内部流场，通过数值模拟可以更直观地观察分析环形管道的主要阻力区及其影响因素。

主要结论如下：

(1)在雷诺数一定的情况下，环形管内阻力系数随着间隙的增大而减小。对于某给定的环形管道，其阻力系数与其对应的雷诺数乘积约等于一个常数，其值大致等于96。

(2)在任何间隙下环形管内的阻力系数总是随着雷诺数的增加而减小，并且当Re>4000以后，阻力系数较雷诺数的增加而变得平缓，最终趋于水平，即管内阻力系数几乎不随雷诺数的增加而减小。环形管道内流体的层流与湍流间的转捩雷诺数随着间隙的增大而增大。

(3)运用Fluent软件对环形管道内流场的模拟结果可知，环形间隙内流体和内管的流体均沿着管道流动方向压力逐渐降低，并且伴随有流速在小范围内升高。

参考文献

[1] 王振铭，王喜魁，洪广欢.分布式能源发展的新机遇[J].沈阳工程学院学报，2012，8(3)：193-197.

[2] 曾和义，秋穗正，苏光辉.环形窄缝通道湍流流动换热特性分析[J].原子能科学技术，2009，43(4)：339-344.

[3] 廖嘉瑜.大型供热管网解决长距离输送热管网的新思路[J].沈阳工程学院学报，2012，8(3)：211-213.

[4] 吴东垠，王利兵，王健，等.一种基于逆流热交换原理的输热三层套管系统：中国，ZL201110102653.7[P].2012-09-05.

[5] 范佳，冯殿义.环形流道流体阻力特性实验研究[J].实验流体力学，2011，25(1)：13-16.

[6] 赵振兴，杨震，郭琴琴，等.螺旋管换热器同轴环形通道流动特性实验[J].重庆大学学报，2011，34(1)：116-120.

[7] 郭楚文，李意民，陈更林.工程流体力学[M].2版.徐州：中国矿业大学出版社，2010.

doi:10.3969/j.issn.1009-8984.2015.02.014

收稿日期：2015-06-10

基金项目：国家自然科学基金(51376148)

作者简介：徐凯(1991-)，男(汉)，西安，硕士

中图分类号：TK121

文献标志码：A

文章编号：1009-8984(2015)02-0051-05

The resistance calculation and simulation analysis to annular pipeline

XU Kai，et al.

(SchoolofEnergyandPowerEngineering，Xi’anJiaotongUniversity，Xi’an710049，China)

Abstract：The annular pipeline has been widely used for its significant advantages of the compact construction，the large heat transfer area，the good fluidity，the high heat transfer coefficient，and so on.Firstly，the paper calculates the resistance character of annular pipeline，and analyzes Reynolds numbers，annular pipeline gap，and the influence of equivalent diameter to resistance coefficient.It finds that the product of resistance coefficient and the corresponding Reynolds numbers is a constant for some specific annular pipelines，and the value is about 96.Secondly，the Fluent software is used to make numeral simulate to the inside flow in annular pipeline.It finds that the inside flow in annular pipeline gap will reduce gradually by the gradual reduce of the flowing direction pressure in pipeline，and with the increase of flow rate in a small range.

Key words：annular pipeline；resistance character；numerical simulation