单桩荷载—沉降曲线拟合线性回归法研究

单桩荷载—沉降曲线拟合线性回归法研究

主要研究结构工程。

国伟

(长春工程学院土木工程学院，长春130012)

摘要：对现有的单桩荷载沉降曲线拟合方法——指数函数线性回归法，按照一定的方法进行优化和改进，提出了指数加权拟线性回归法。通过对单桩静载荷试验数据进行拟合，结果表明加权拟线性回归法拟合效果好于传统指数函数线性回归法。指数加权拟线性法对单桩荷载—沉降曲线模型能进行比较好的描述，在沉降预测中得出更加精确的结论。因此，可以利用指数函数加权拟线性法的拟合结果对单桩承载力进行预测。

关键词：指数函数线性回归法；指数函数加权拟线性回归法；荷载—沉降曲线

0前言

桩竖向极限承载力在桩基工程中是一个很重要的参数，评价和预测桩的承载力，可以通过单桩静载荷试验来确定。然而对于利用静载荷试验得到的不完整的实测数据，目前提出了多种数学模型预测方法，其中主要包括：双曲线模型、指数曲线模型、完整指数曲线模型和人工神经网络预测模型等拟合出完整的荷载—沉降曲线。其中，指数曲线和双曲线都是根据前期实测沉降数据进行沉降推算，比起完整指数曲线模型，人工神经网络预测模型简单很多，容易计算，便于工程技术人员的应用。文献[1-2]研究得出，指数曲线对桩基沉降的预测相对于双曲线沉降预测更加准确，因此，本文采用指数曲线模型进行拟合。而文献[1，3]对于指数函数曲线模型，都采用线性回归法进行预测，先将其换元线性化，然后利用标准一元线性回归的方法求解待定的参数。但是，这种做法忽略了换元后的因变量误差的异方差性，并不满足标准一元线性回归的基本假设——因变量的观测误差应服从均值为零、方差相等的正态分布，所以，运用这种方法求解的参数是有偏差的，而且精度较低，由此得到的曲线方程用于预测时往往会带来较大的偏差。因此，为了进一步提高拟合精确度，本文将简述改进后的指数线性回归方法(加权拟线性回归法)。并通过实例，将指数函数换元线性回归法与加权拟线性回归法以及非线性回归法的拟合结果进行比较。

1指数拟线性回归简介

1.1指数函数传统解法(线性回归法)

普通指数拟合方程：

y=aebx。

(1)

然后采用一元线性回归法求得a、b，具体的计算步骤可以参看文献[3]。

1.2指数函数线性回归方法的改进(指数加权拟线性回归法)

根据文献[4]的研究可以得出换元线性回归法回归的本质、存在的问题和精度的评定，以及换元线性回归法的改进措施和2种方法求解的参数精度比较。

1.2.1普通指数函数线性回归存在的问题

普通指数函数的观测方程可写作

yk=aebxk+ζk(k=1，2，3，…，n)，

(2)

ζk为yk的测量偶然误差，并且ζk-N(0，σ2)。而通过一元线性回归法求解得

yk′=a′+bxk+ik，

(3)

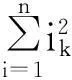
1.2.2普通指数函数线性回归法的改进措施

将式(3)两端同时乘以yi，新观测方程为

ykyk′≈yka′+ykxkb+ζk，

(4)

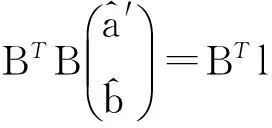
(5)

求得a、b，从文献[4]得出用线性回归方法求解的a、b，大于或等于用改进后的方法求解的a、b。因此，指数加权拟线性回归法的精度高于普通指数线性回归法。

2实验与分析

2.1实验数据

为取得辽宁省一工程钢筋混凝土桩基础设计依据，抽取一根桩做静载实验，我们取其中一根桩的实验数据做沉降曲线拟合。桩型为边长0.55 m，长38 m的钢筋混凝土方桩，内空腔直径0.3 m，混凝土标号30号。试桩的荷载沉降资料见表1。

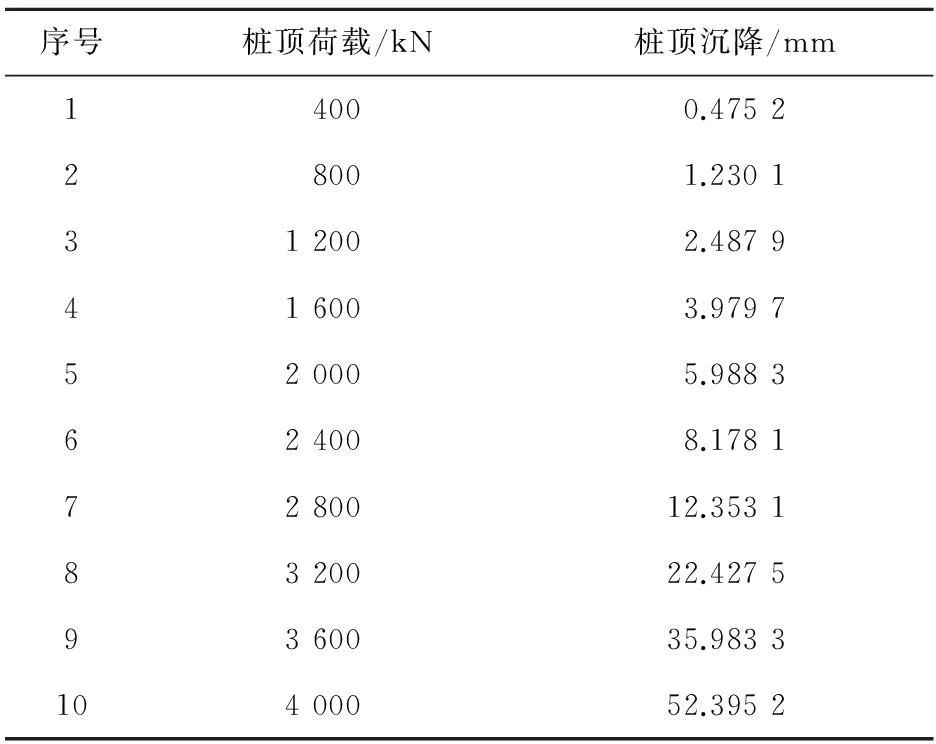
表1　试桩的荷载沉降值

2.2实验结果

现用指数换元线性化方法、改进的线性化方法和非线性最小二乘法对表1静载实验数据进行回归计算，结果列于表2，荷载—沉降拟合曲线如图1，纵坐标是位移(mm)，横坐标是荷载(kN)。

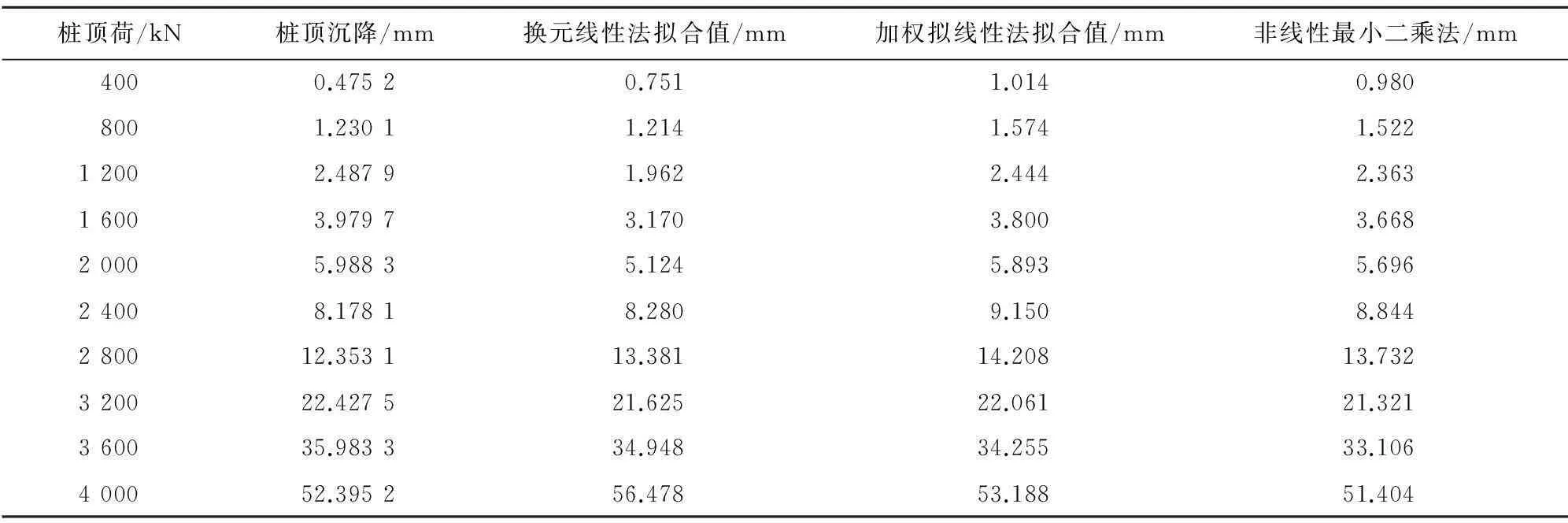
表2　2种曲线拟合结果

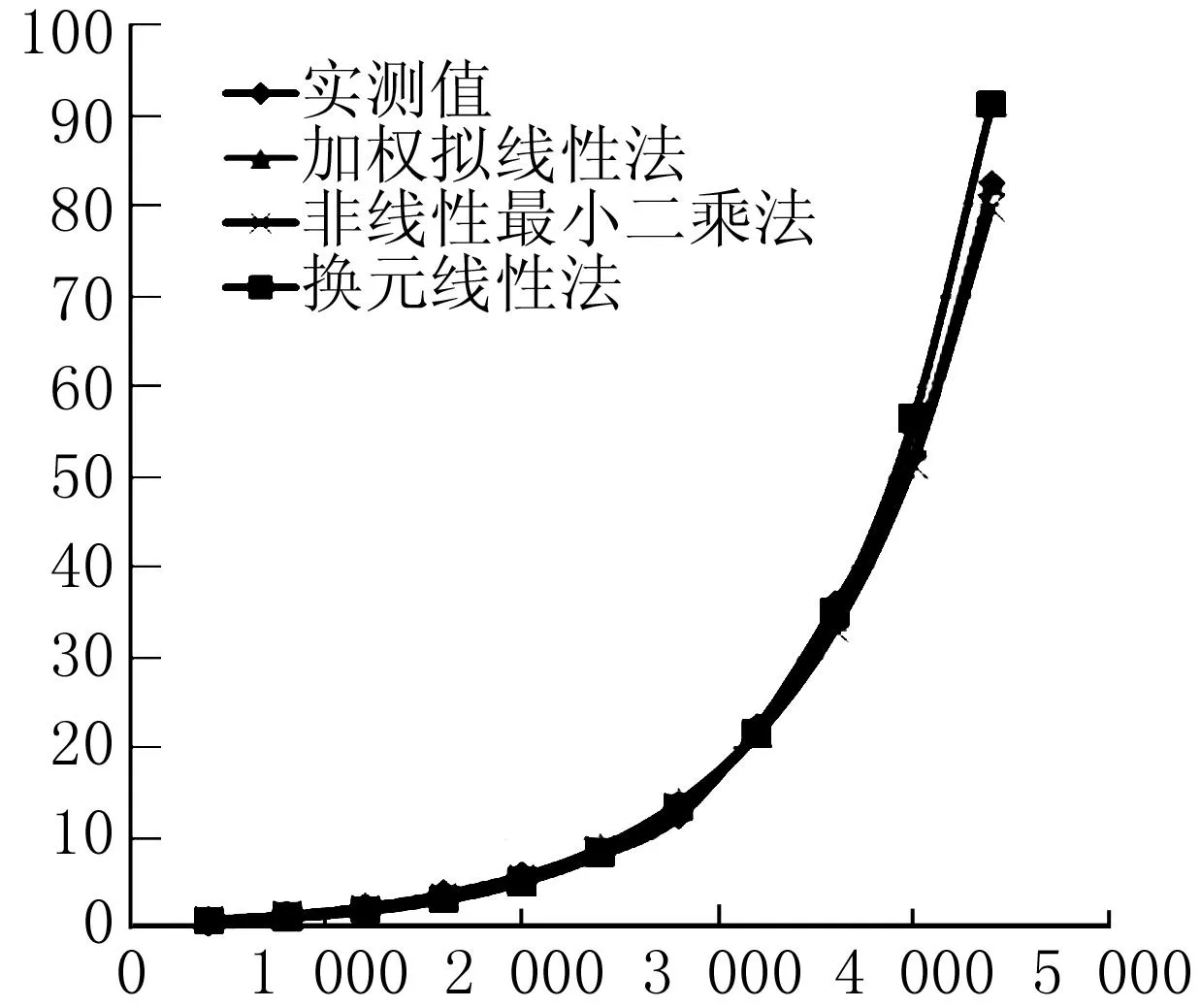
图1　试桩荷载—沉降曲线对照图

从表3可以看出改进的指数线性化方法与非线性最小二乘法相比，所求参数及其精度十分接近，而换元线性化方法与非线性化方法相比，参数差异比较大，且前者的精度比较低。很明显，非线性回归曲线及改进的线性回归曲线与散点拟合较好，而用指数换元线性化方法所获得的回归曲线与散点拟合较差些。

表3　3种曲线参数和误差比较

3结语

通过指数线性回归法、改进的线性回归方法和非线性最小二乘法的曲线拟合比较，这3种方法都可以对单桩承载力进行预测，其中拟合较好的是改进的指数线性回归法和非线性最小二乘法曲线拟合。因此，指数加权拟线性回归法对单桩荷载—沉降曲线模型能进行比较好的描述，可以利用指数加权拟线性回归法拟合结果对单桩承载力进行预测。总之，在实验数据拟合过程中，采用指数加权拟线性法拟合可以有效减小拟合误差，经过实际数据检验，可以有效提高精度，在实际工作中有参考价值。

参考文献

[1] 邓志勇，陆培毅.几种单桩竖向极限承载力预测模型的对比分析[J].岩土力学，2002，23(4):428-431.

[2] 周鑫，张强，曾亦衡.指数曲线与双曲线在软基沉降预测中的对比分析[J].探矿工程(岩土钻掘工程)，2011，38(11):52-58.

[3] 谢耀峰，吴芳银，王云球.试桩未达极限状态时桩的极限承载力预测[J].水运工程，2002，344(9):5.

[4] 王仲峰，冯仲科.几种一元拟线性回归中的问题与改进措施[J].东北师大学报(自然科学版)，2006(4):45-52.

[5] 赵春风，李尚飞，鲁嘉，等.完整指数函数拟合单桩荷载—沉降曲线的分析[J].同济大学学报(自然科学版)，2010，38(4):486-491.

[6] 王仕伟，王雪峰.基桩—荷载沉降曲线拟合与分析[D].武汉：华中科技大学，2007.

[7] 欧阳明，丁伯阳，石吉森.单桩荷载—沉降曲线的修正指数曲线模型拟合研究[J].水运工程，2003，474(1):32-36.

doi:10.3969/j.issn.1009-8984.2015.02.006

收稿日期：2015-06-04

作者简介：国伟(1989-)，男(汉)，山东临沂，硕士

中图分类号：TU433

文献标志码：A

文章编号：1009-8984(2015)02-0021-03

The study on single pile load-settlement curve fitting linear regression method

GUO Wei

(SchoolofCivilEngineering，ChangchunInstituteofTechnology，Changchun130012，China)

Abstract：In this article，the existing single pile load-settlement curve fitting methods-exponential function linear regression method has been optimized and improved according to certain method，and the exponential function weighted quasi fitting linear regression method has been put forward.Through the fitting to single pile static load test data，the results show that the fitting effect of weighted quasi fitting linear regression method is better than traditional exponential function linear regression method.Exponential function weighted quasi fitting linear method of single pile load-settlement curve model can make a better description，and get more accurate conclusion in settlement prediction.So the forecast of single pile bearing capacity can be made by taking advantage of the result of exponential function weighted quasi fitting linear method.

Key words：exponential function linear regression method；exponential function weighted quasi fitting linear regression method；load-settlement curve