一类积分边值问题解的存在性与唯一性

一类积分边值问题解的存在性与唯一性

主要研究常微分方程理论与应用。

赵坤

(佳木斯大学理学院数学部，黑龙江 佳木斯 154007)

摘要：利用Schauder不动点定理和上下解方法，研究了一般二阶非线性常微分方程满足一类积分边值条件的解的存在性和唯一性。

关键词：积分边值问题；Leray-Schauder度理论；上下解方法；Nagumo条件

0引言

边值问题是微分方程研究领域中的一类重要问题，最初的研究可追溯到19世纪30年代Strum和Liouville对二阶线性方程的边值问题的求解，20世纪Hilbert等众多数学家和物理学家为边值问题奠定了理论基础，研究的重点也转向一般的非线性微分方程的各类边值问题。随着非线性分析理论快速发展和许多具有实际应用背景问题的推动，边值问题的理论和方法发展十分迅速，不仅在经典的二阶常微分方程两点边值问题方面，而且在多点边值问题[1-2]、积分边值问题[3-6]，乃至高阶微分方程[7]和分数阶微分方程[8]的边值问题等方面，都涌现出许多重要的工作，并由此形成了许多新的研究方向。

本文利用Schauder不动点定理和上下解方法[9-11]考虑如下积分边值问题：

y″=f(x，y，y′)，

(1)

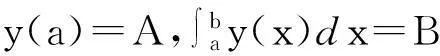
(2)

解的存在性和唯一性。为方便叙述，首先简要介绍一些基本概念和结果，详细论述可参见文献[11]。

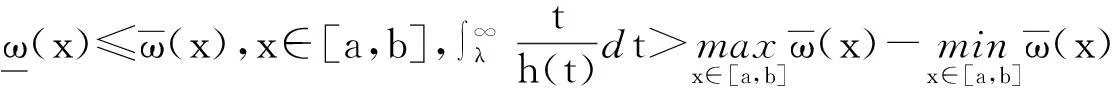
其中

|F(x，y，z)|≤h(|z|)，

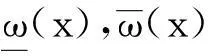
y″=F(x，y，y′)

|y′(x)|≤N，x∈[a，b]。

本文的主要结果如下：

定理1假设以下3个条件成立：

(A1)函数f：[a，b]×R×R→R连续；

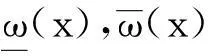
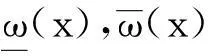
定理2假设函数f(x，y，z)满足：

1)fy(x，y，z)≥0；

2)|fz(x，y，z)|≤M，

那么边值问题(1)～(2)的解存在且唯一。

1主要结果的证明

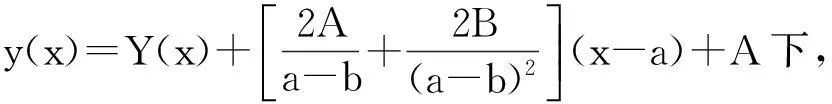
不失一般性，我们假设(2)中的A=B=0。

考虑辅助方程

y″=F(x，y，y′)，

(3)

其中

F(x，y，z)=f(x，p(x，y)，q(z))+r(x，y)，

引理2边值问题(3)、(2)的任何解y(x)都满足

(4)

证明：首先证明：对任意自然数n，有

(5)

因此

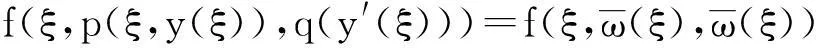
这与假设(A3)中的(c)矛盾。

若η∈(a，b)，则

与η=b情形一样可导出矛盾。

综上知(5)成立。在(5)中，令n→∞，即得(4)成立。引理证毕。

定理1的证明：显然，函数F(x，y，y′)在[a，b]×R×R上有界，设M是它的一个上界。令

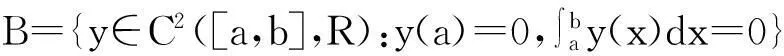
B0={y∈B：||y||≤Q，||y′||≤Q}，

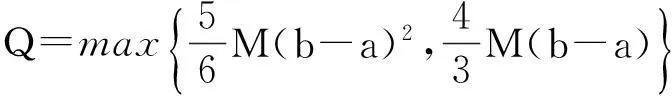
利用Lagrange常数变易公式，方程y″=G(t)满足边值条件(2)的解为

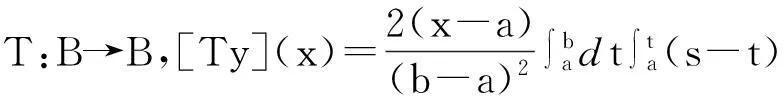
显然，算子T的不动点就是边值问题(3)-(2)的解。

当x∈[a，b]时，有

因此T将B0映入B0。又

|[Ty]″(x)|≤|F(x，y(x)，y′(x))|≤M，

定理2的证明：令

(c)由定理的假设1)和2)，我们有

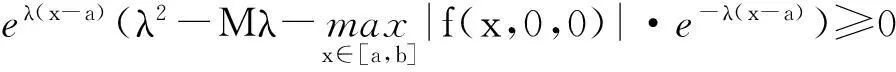
由定理1得边值问题(1)～(2)的解存在。

下面证明解的唯一性。假设y1(x)和y2(x)都是(1)～(2)的解，令u(x)=y1(x)-y2(x)，则u(x)是边值问题

(6)

的解，且

u(ξ)=0，u(x)≠0，x∈(a，ξ)。

由于对任何常数c，cu(x)也是(6)的解。因此存在c0≠0和η∈(a，ξ)，使得

于是有

综上得，边值问题(1)～(2)的解存在且唯一。定理证毕。

参考文献

[1] Palamides P K.Multipoint boundary-value problems at resonance forn-order differential equations：positive and monotone solutions[J].Electron Journal of Differential Equations，2004(5)：1-14.

[2] Liu Jian，Feng Han-ying，Feng Xing-fang.Multiplicity of positive solutions for a singular second-order three-point boundary value problem with a parameter[J].Journal of Applied Mathematics，2014(4)：8.

[3] Chen Guo-ping，Shen Jian-hua.Intergral boundary value problems for first order impulsive functional differential equations[J].Int.Journal of Math，2007，1(20)：965-974.

[4] Yang Zhi-lin.Existence and nonexistence resuts for positive solutions of an intergral boundary value problem[J].Nonlinear Analysis：Theory，Methods & Applications，2006，65(8)：1489-1511.

[5] Yang Zhi-lin.Positive Solutions of a second-order integral boundary value problem[J].Journal of Mathematical Analysis and Applications，2006，321(2)：751-765.

[6] DE Hoog F R，Mattheij R M M.On the conditioning of multipoint and integral boundary value problems[J].SIAM Journal of Mathematical Analysis，1989，20(1)：200-214.

[7] Agarwal R P.Boundary Value Problems for Higher Order Differential Equations[M].Singapore:World Scientific，1986.

[8] Mahmudov N I，Unul S.Existence of solutions ofα∈(2，3] order fractional three-point boundary value problems with integral conditions[J].Abstract and Applied Analysis，2014，20：12.

[9] Bernfeld S R，Lakshmikantham V.An Introduction to Nonlinear Boundary Value Problems[M].New York：[s.n.]，1974.

[10] Kannan R，Lakshmikantham V.Existence of periodic solutions of nonlinear boundary value problems and method of upper and lower solutions[J].Applicable Analysis：An International Journal，1984，17(2)：103-113.

[11] 章国华，侯斯.非线性奇异摄动现象：理论和应用[M].福州：福建科学技术出版社，1989.

[12] 钟承奎，范先令，陈文塬.非线性泛函分析引论[M].兰州：兰州大学出版社，2004.

doi:10.3969/j.issn.1009-8984.2015.02.033

收稿日期：2015-04-03

基金项目：黑龙江省教育厅面上课题(12541829)

作者简介：赵坤(1978-)，女(汉)，黑龙江佳木斯，讲师

中图分类号：O175.1

文献标志码：A

文章编号：1009-8984(2015)02-0125-04

The existence and uniqueness of the solution to a class of integral boundary value problem

ZHAO Kun

(MathematicsDepartment，SchoolofSciences，JiamusiUniversity，JiamusiHeilongjiang154007，China)

Abstract：In this article，by using the fixed point theorem of Schauder and the upper and lower solution method，the existence an uniqueness of the solution met a class of integral boundary value conditions in general second-order nonlinear differential equations have been studies.

Key words：integral boundary value problem；the theory of Leray-Schauder degree；upper and lower solution method；Nagumo condition